Approximations des intégrales
Objectives
Dans certain problèmes issus de la physiques ou chimie (mais aussi en Mathématiques!)
on est amené à calculer des intégrales (par exemple pour la résolution numérique des équations
différentielles ou en statistiques, ...).
Généralement ces intégrales ne sont pas facile à calculer, les difficultés qu'on
peut rencontrer sont de deux types:
- $\rhd$ Pour certaines fonctions, on ne sais pas exprimer leur primitives à l'aide des fonctions usuelles,
bien que l'existence de leurs primitives est assurés.
Un exemple classique : $x\rightarrow \ee^{-x^2}$. - $\rhd$ En générale, on ne dispose pas de la fonction $f$, mais uniquement de quelques valeurs de $f$. i.e on connaît $f(x_i)_{1\leq i\leq n}$.
Soient $-\infty < a< b< \infty$ deux réels et $f$ une fonction définie sur $[a,b]$ à valeurs dans $\R$.
Pour $n\in \N^*$, on se donne une
Méthodes classiques
Somme de Riemann
L'idée principale de cette méthode est d'approcher la fonction $f$ sur $[a,b]$ par une fonction constante proche
de la fonction $f$, souvent on prend $f(\zeta)$ pour un certain $\zeta\in [a,b]$.
On parle de
-
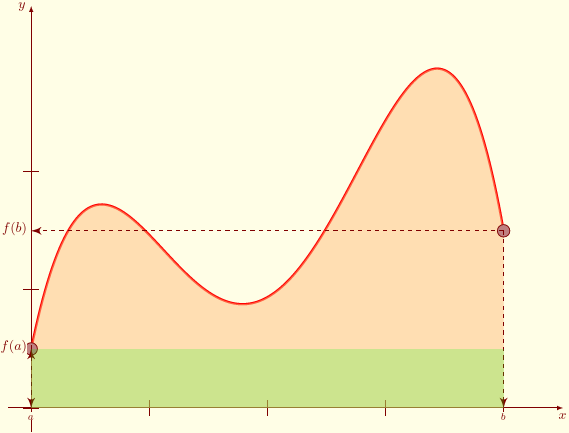
Méthode de rectangle à gauche lorsque on prend $\zeta = a$.
-
Méthode de rectangle à droite lorsque on prend $\zeta=b$.
-
Méthode de point du milieu lorsque on prend $\zeta=\dfrac{a+b}{2}$.
On suppose que $f\in \CC^1([a,b])$, alors $$\forall n\in \N^*,\quad \abs{\int_a^bf(t)\ud t-\dfrac{b-a}{n}\dsum_{k=0}^{n-1}f(a_k)}\leq \dfrac{(b-a)^2}{2n}\norme{f'}_\infty.$$
- Ce résultat reste valable pour la méthode de rectangle à droite ou le point du milieu.
- On peut écrire alors, en notant $R_g(f,n)=\dfrac{b-a}{n}\dsum_{k=0}^{n-1}f(a_k)$, $$\int_a^nf(t)\ud t=R_g(f,n)+\underset{n\to\infty}{\mathrm{o}}\left(\frac{1}{n}\right).$$
- Si $f$ est plus régulière (au moins de classe $\CC^2$), alors la méthode de point du milieu est plus précise, en effet on a le théorème suivant
On suppose que $f\in \CC^2([a,b])$, alors pour tout $n\in \N^*$, $$ \abs{\int_a^bf(t)\ud t-\dfrac{b-a}{n}\dsum_{k=0}^{n-1}f\left(\frac{a_k+a_{k+1}}{2}\right)}\leq \dfrac{(b-a)^3} {24n^2}\norme{f''}_\infty.$$
from math import *
def RM(a,b,n,f):
h = (b-a)/n
S = 0.0
ak = a+h/2.
for i in range(n):
S+= f(ak)
ak+=h
return S*h
def f(x):
return 1/(1.+x)
I = RM(0,1,10,f)
print("Rm = {:.9f}, |Em|={:.9f}".format(I,abs(I-log(2.))))
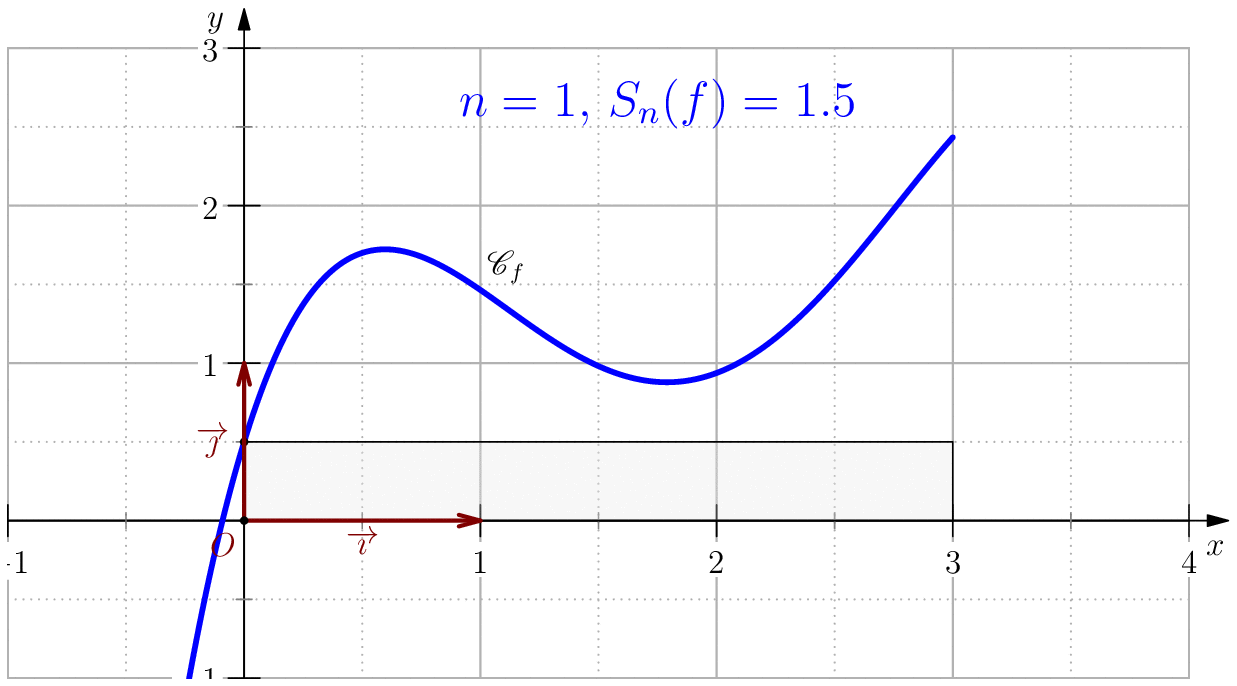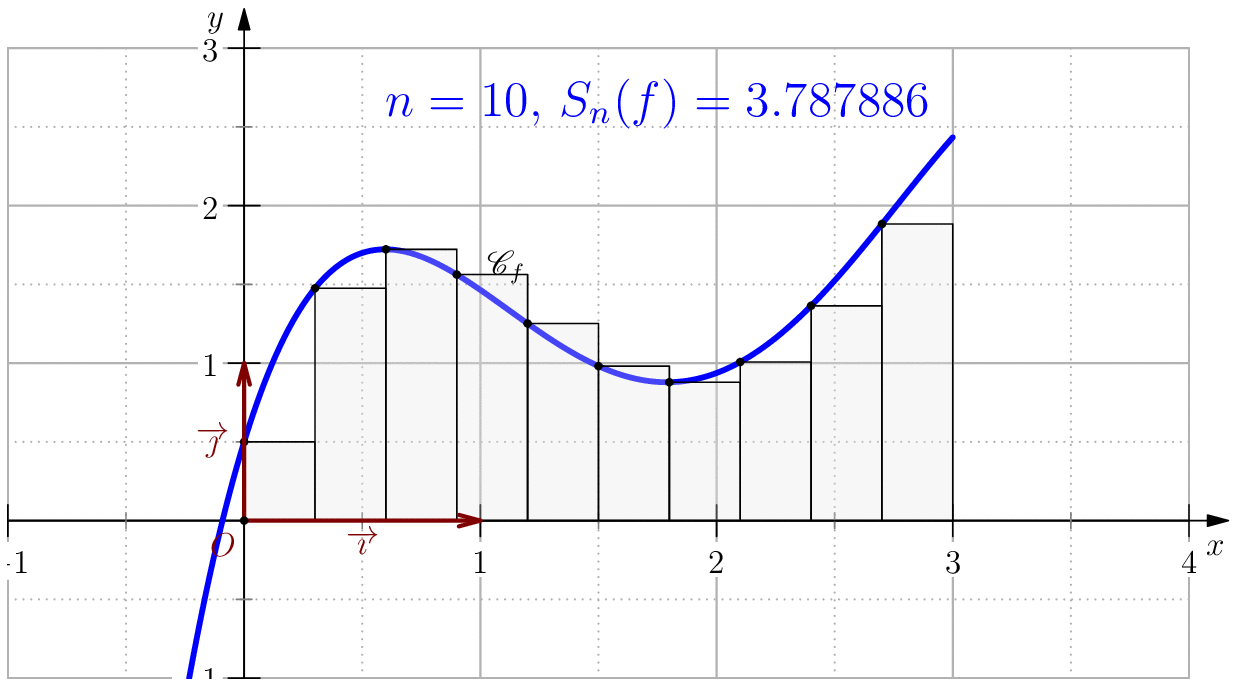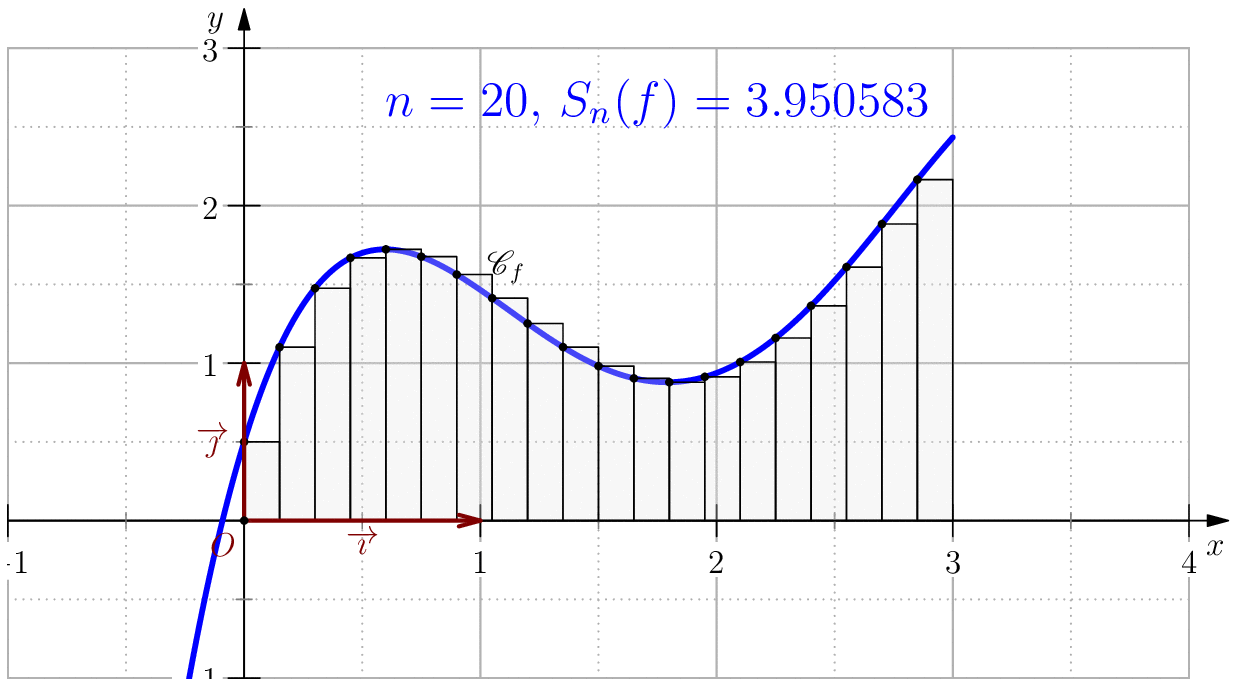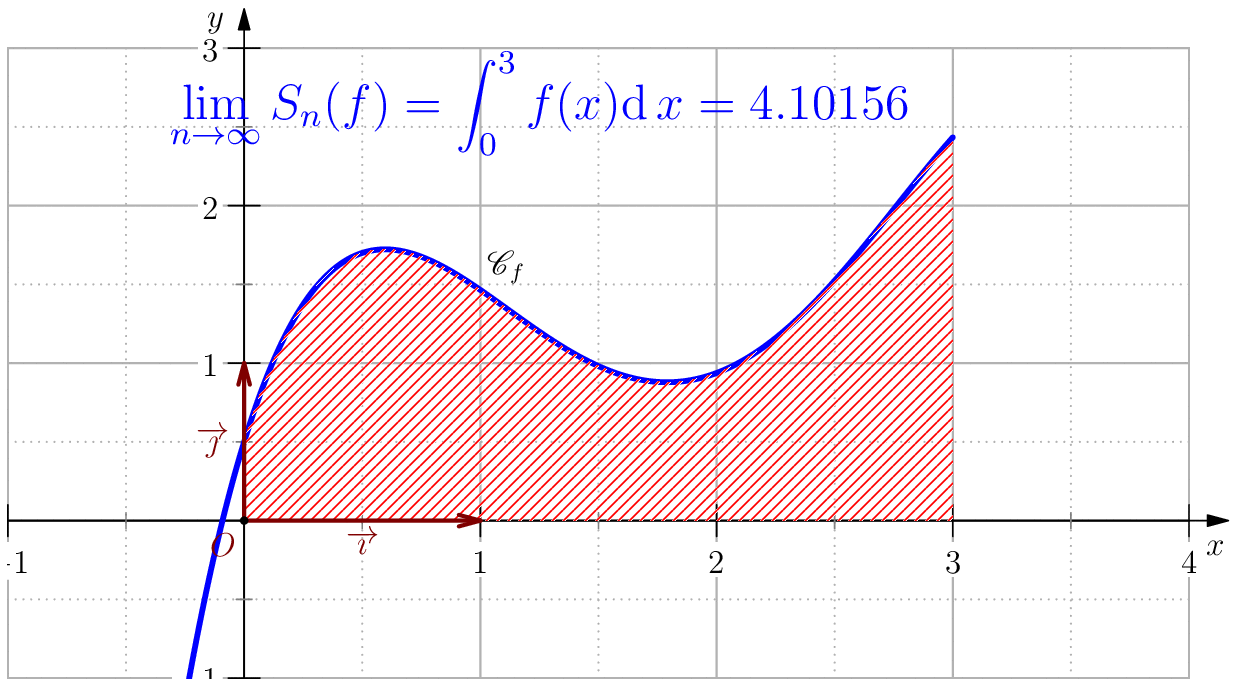
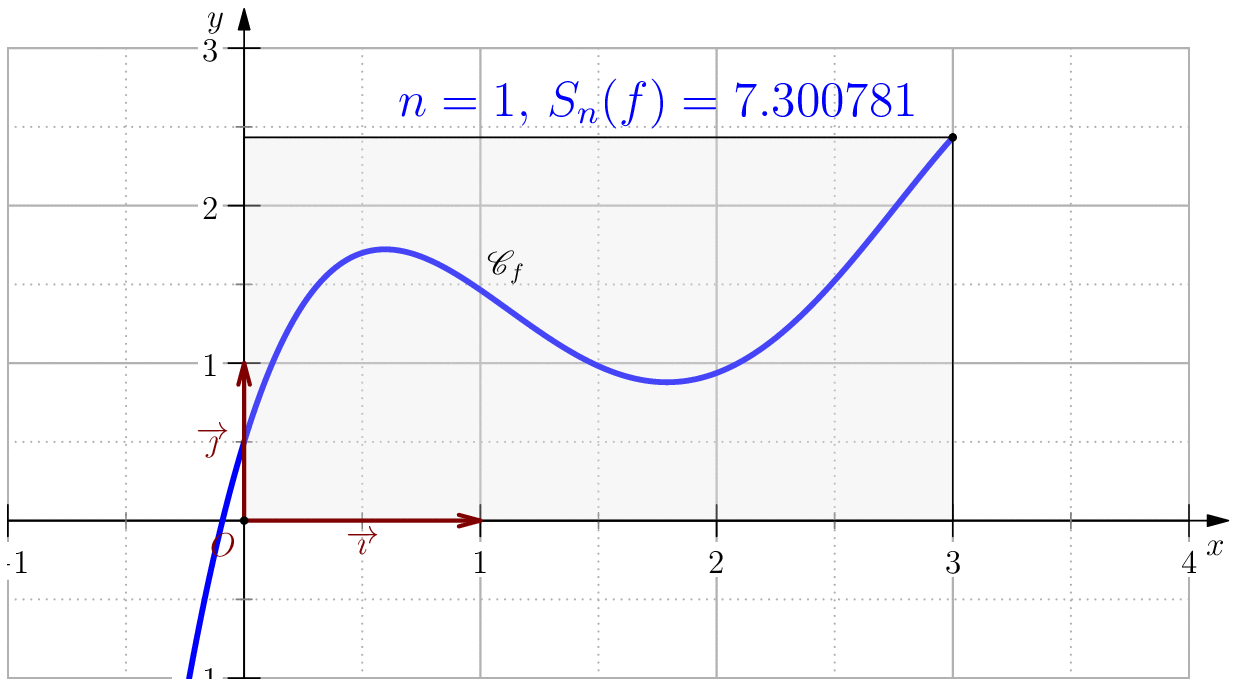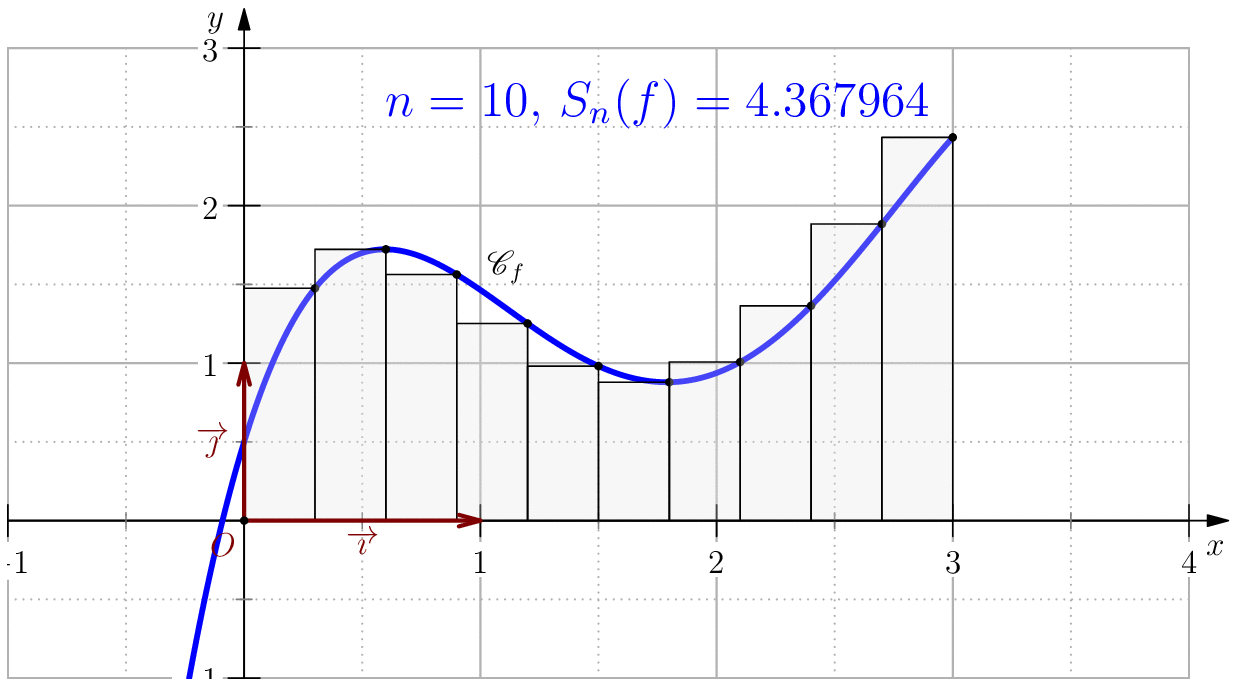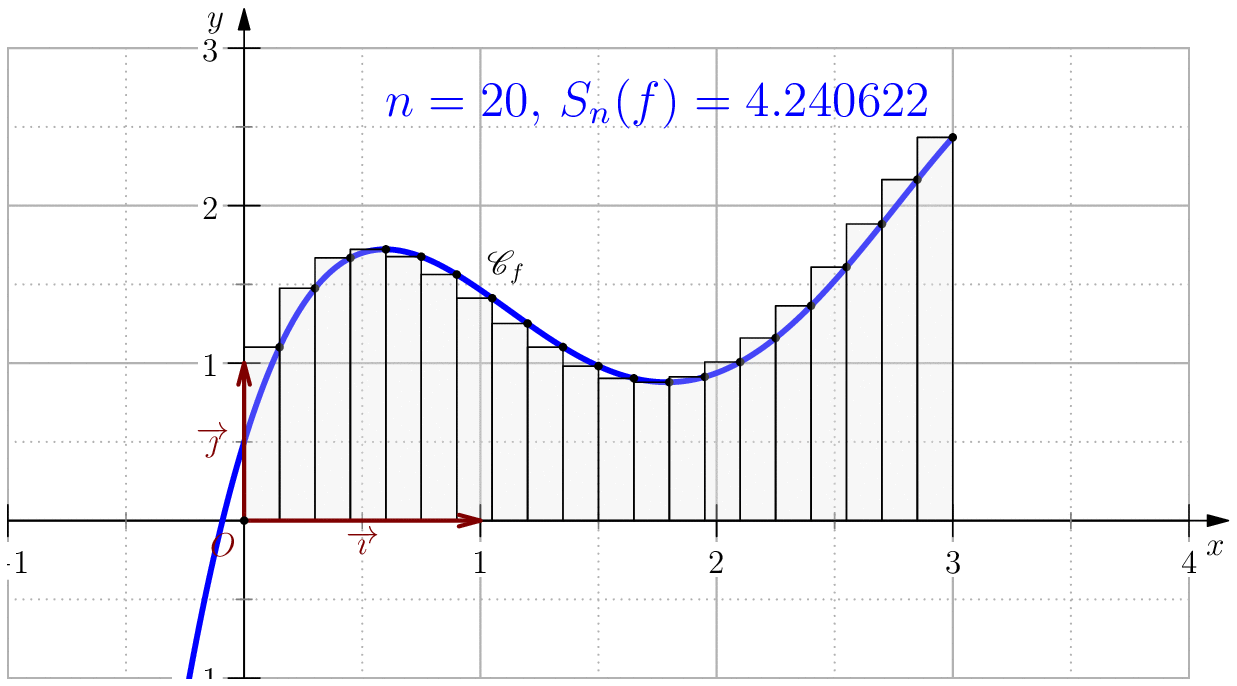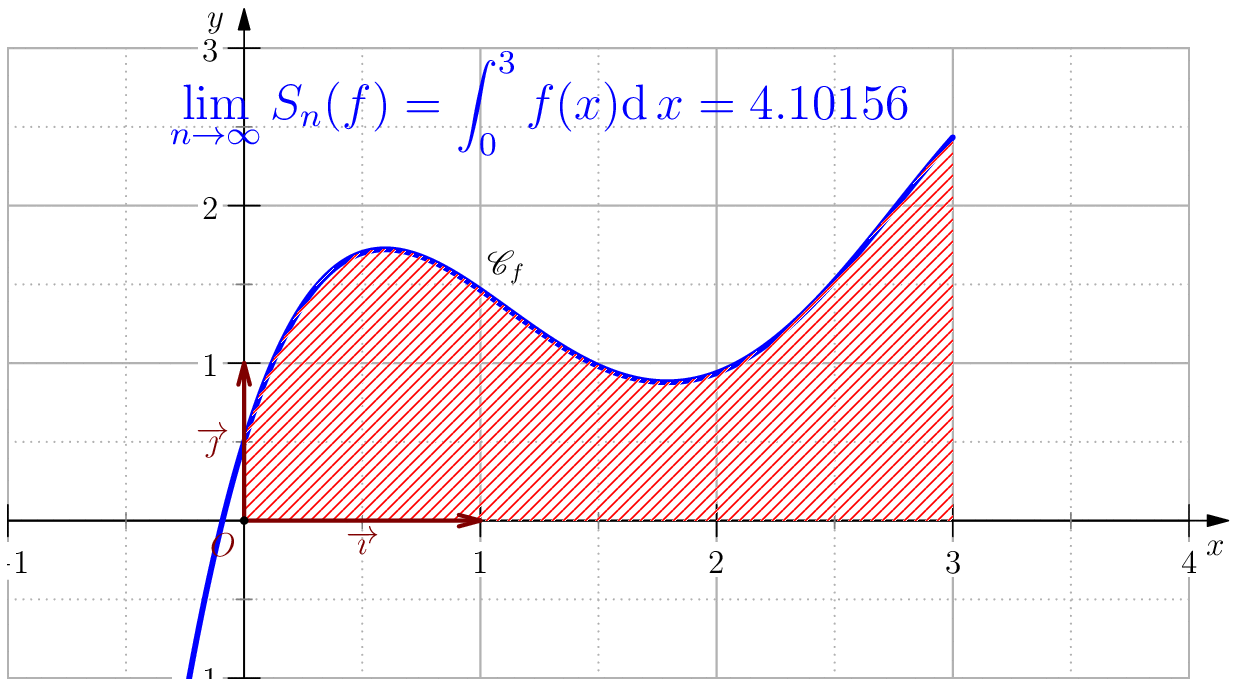
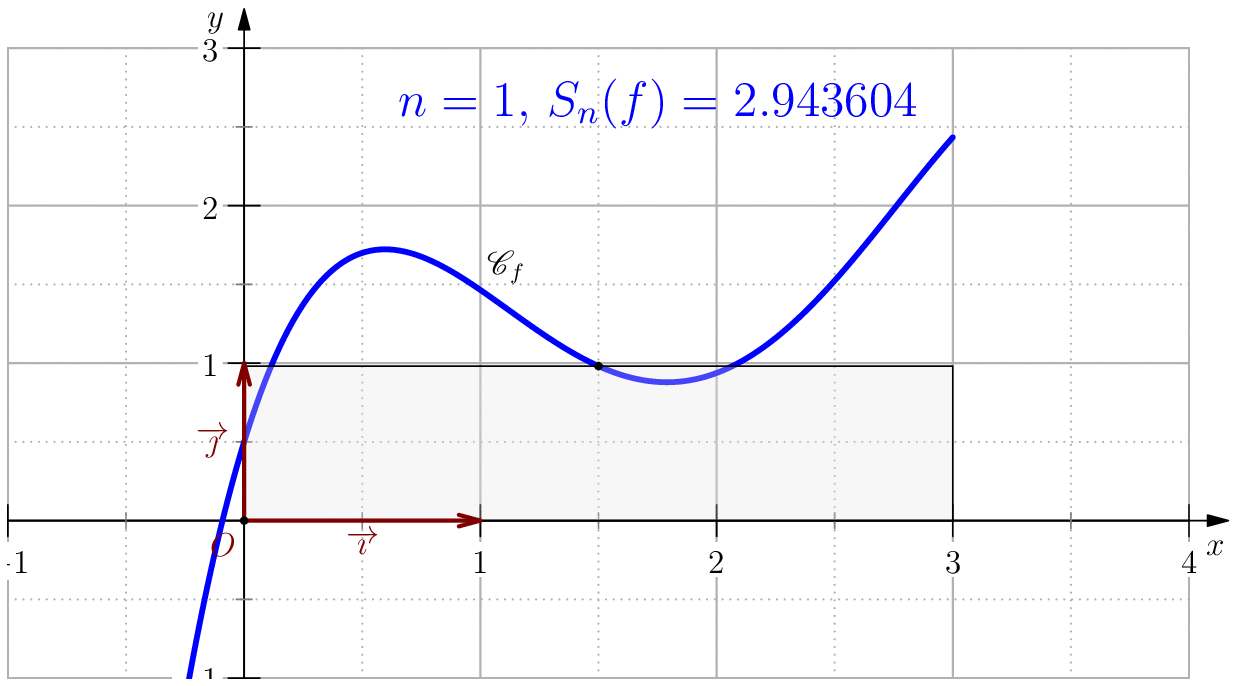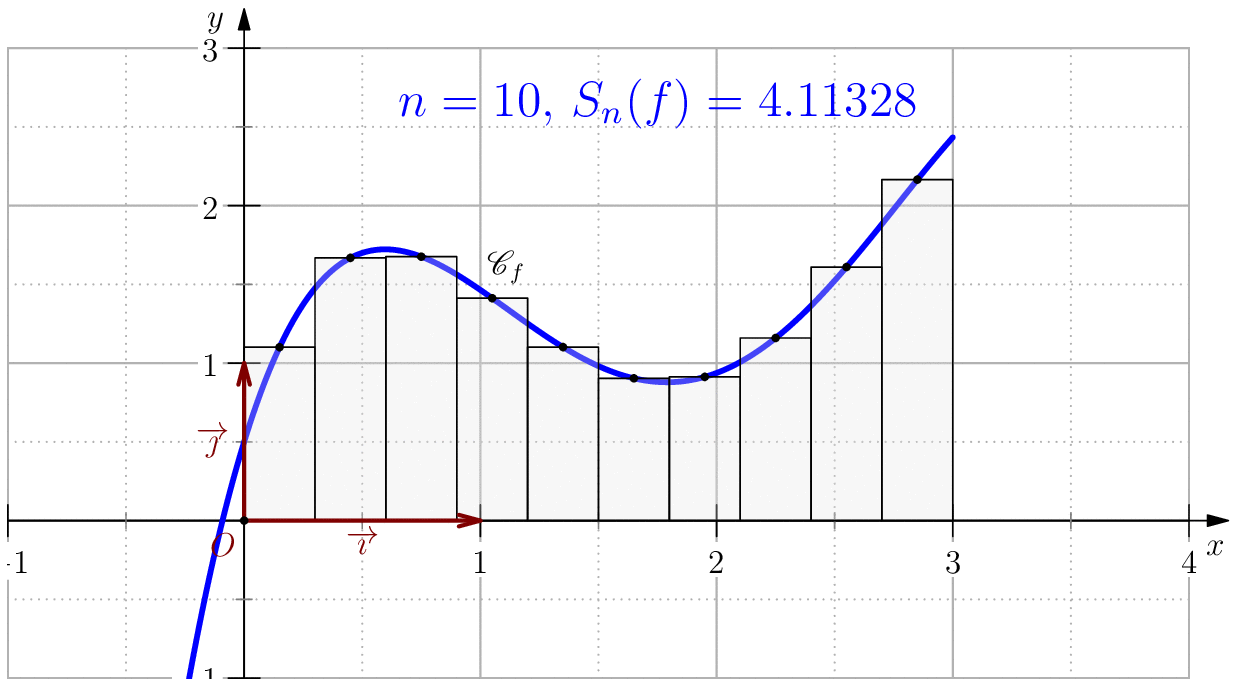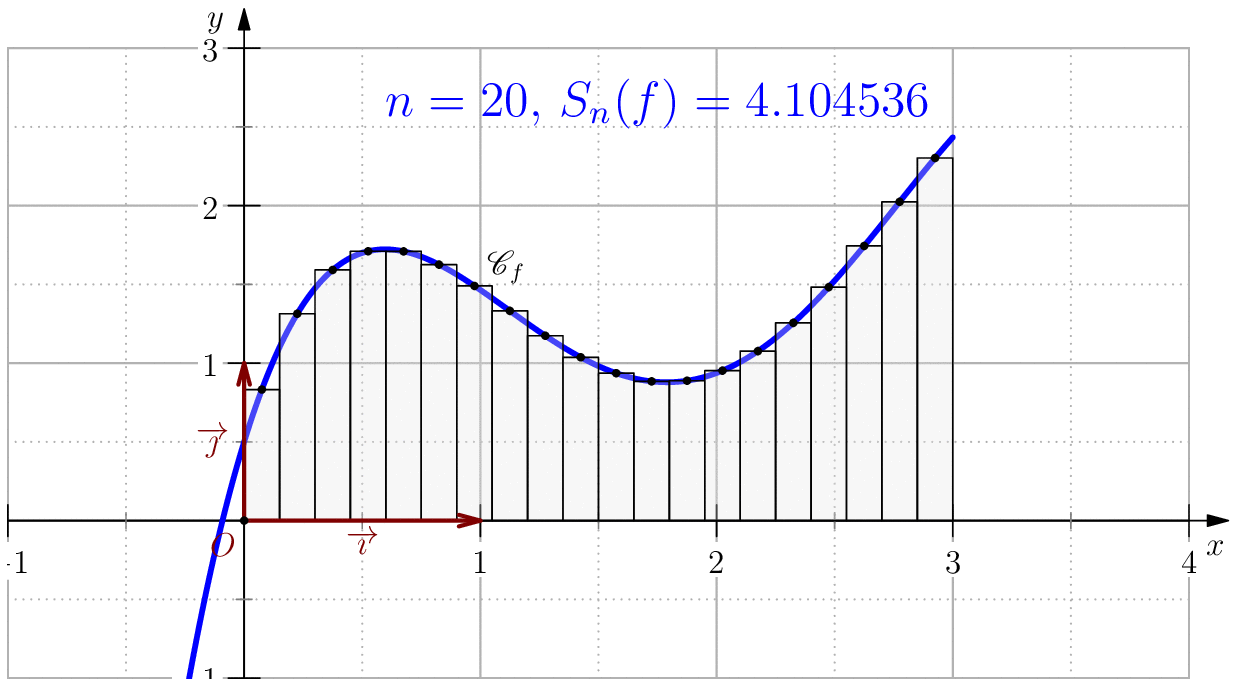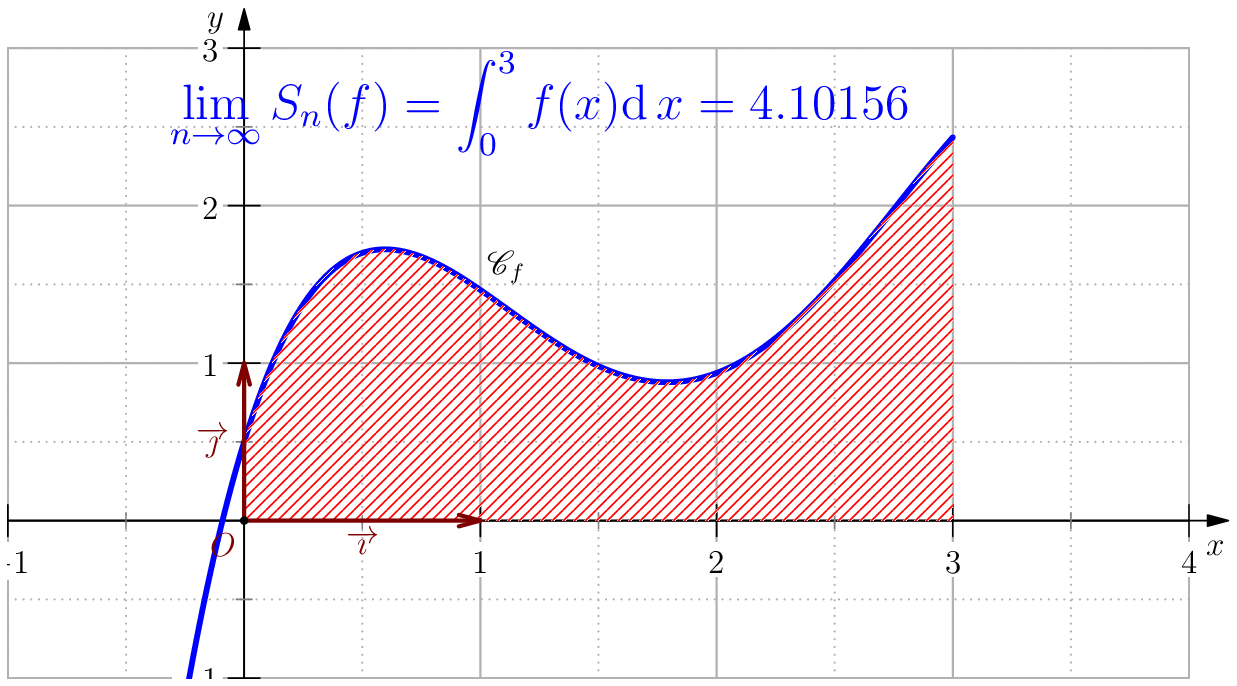
On pose $$f(x)=-\dfrac{85}{256}x^4+\dfrac{165}{64}x^3-\dfrac{197}{32}x^2+\dfrac{39}{8}x+\dfrac{1}{2}$$ alors, $$\dsp \int f(x)\ud x=-(17/256)x^5+(165/256)x^4-(197/96)x^3+(39/16)x^2+(1/2)x$$ En particulier, $$\int_0^3 f(x)\ud x= \dfrac{525}{128}=4.1015625$$
- Convergence de la somme de Riemman (rectangle à gauche). (Animation en pdf)
- Convergence de la somme de Riemman (rectangle à droite).
(Animation en pdf)
- Convergence de la somme de Riemman (point du milieu).
(Animation en pdf)
Méthode de trapèzes
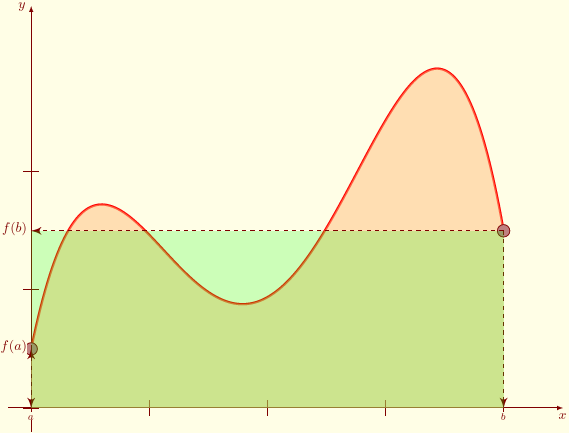
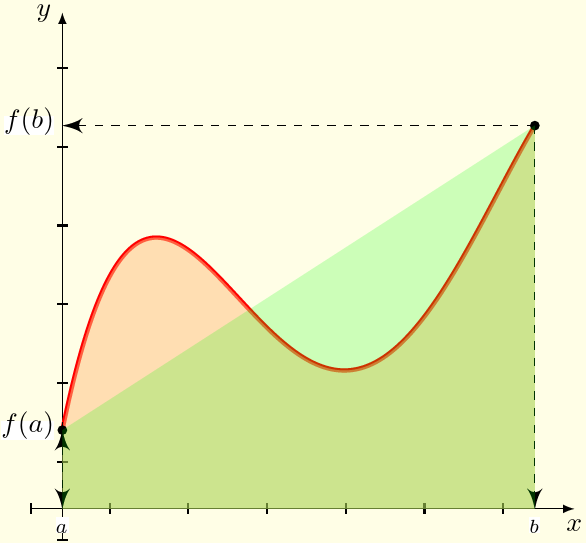
L'idée principale de cette méthode est d'approcher la fonction $f$ sur $[a,b]$ par une fonction affine qui passe par les points $(a,f(a)),\,(b,f(b))$, i.e. $$f(t)\simeq\dfrac{f(b)-f(a)}{b-a}(t-a)+f(a).$$ Ainsi, $\dsp\int_a^bf(t)\ud t\simeq\int_a^b\left(\dfrac{f(b)-f(a)}{b-a}(t-a)+f(a)\right)\ud t.$ Ce qui donne $$\boxed{\dsp\int_a^bf(t)\ud t\simeq(b-a)\dfrac{f(a)+f(b)}{2}}.$$
Pour $n\in \N$, on note $T_n(f)=\dfrac{b-a}{2n}\dsum_{k=0}^{n-1}\left(f(a_k)+f(a_{k+1})\right)$.
- On peut également écrire $$T_n(f)=\dfrac{b-a}{n}\left(\dfrac{f(a)+f(b)}{2}+\dsum_{k=1}^{n-1}f(a_k)\right).$$
- On remarque également $$T_n(f)=\dfrac{R_d(f,n)+R_g(f,n)}{2}.$$
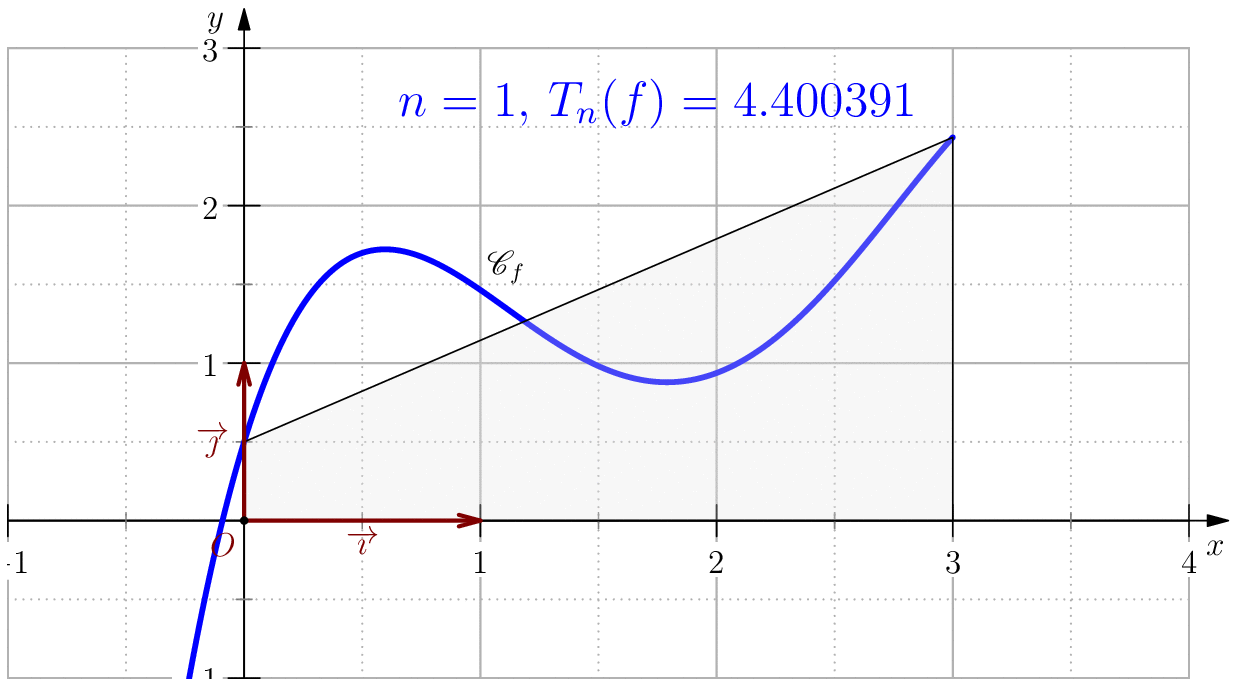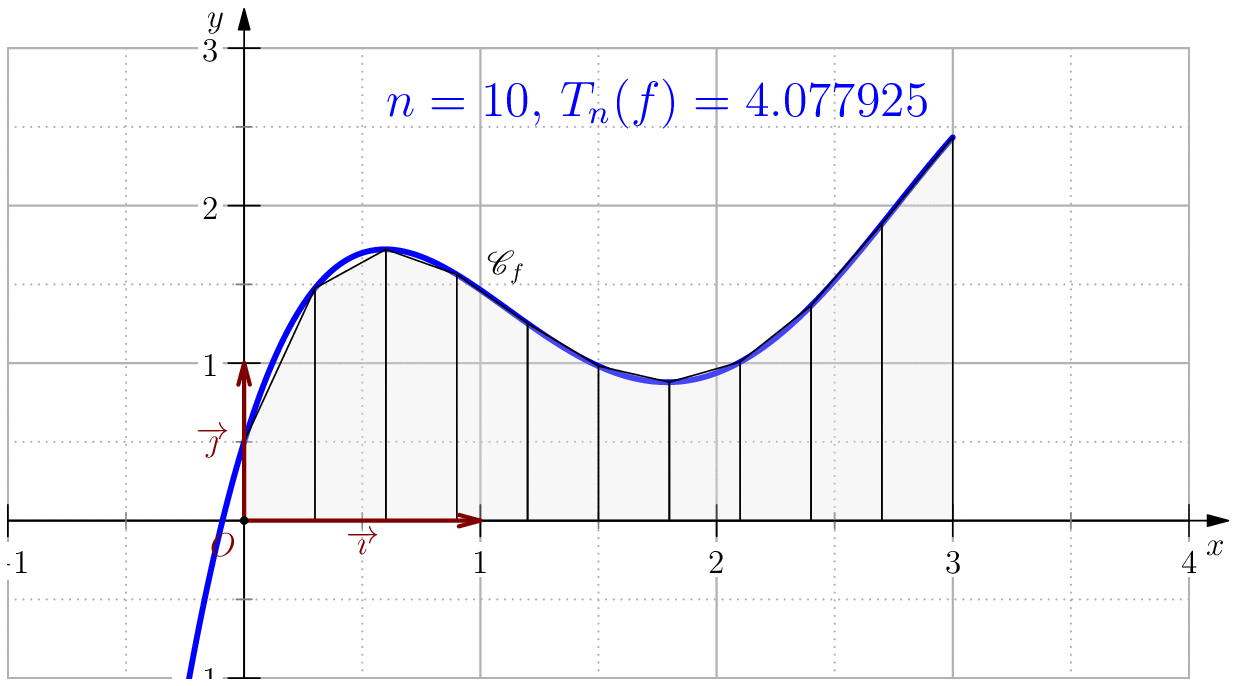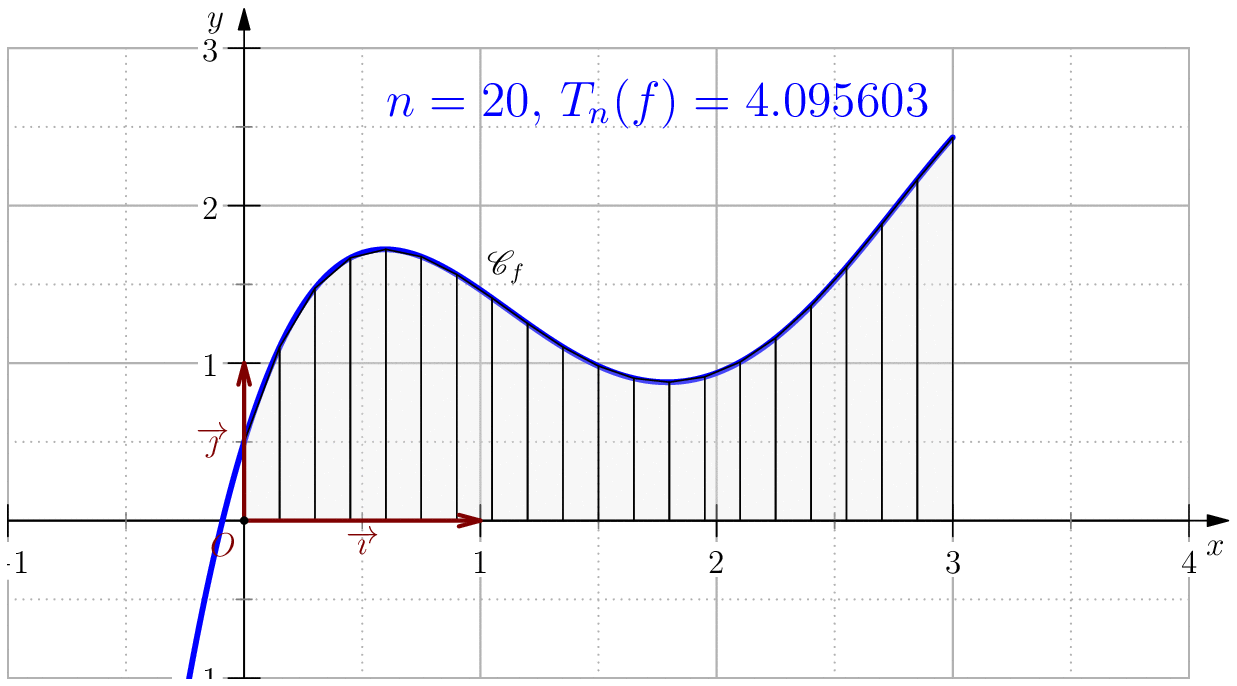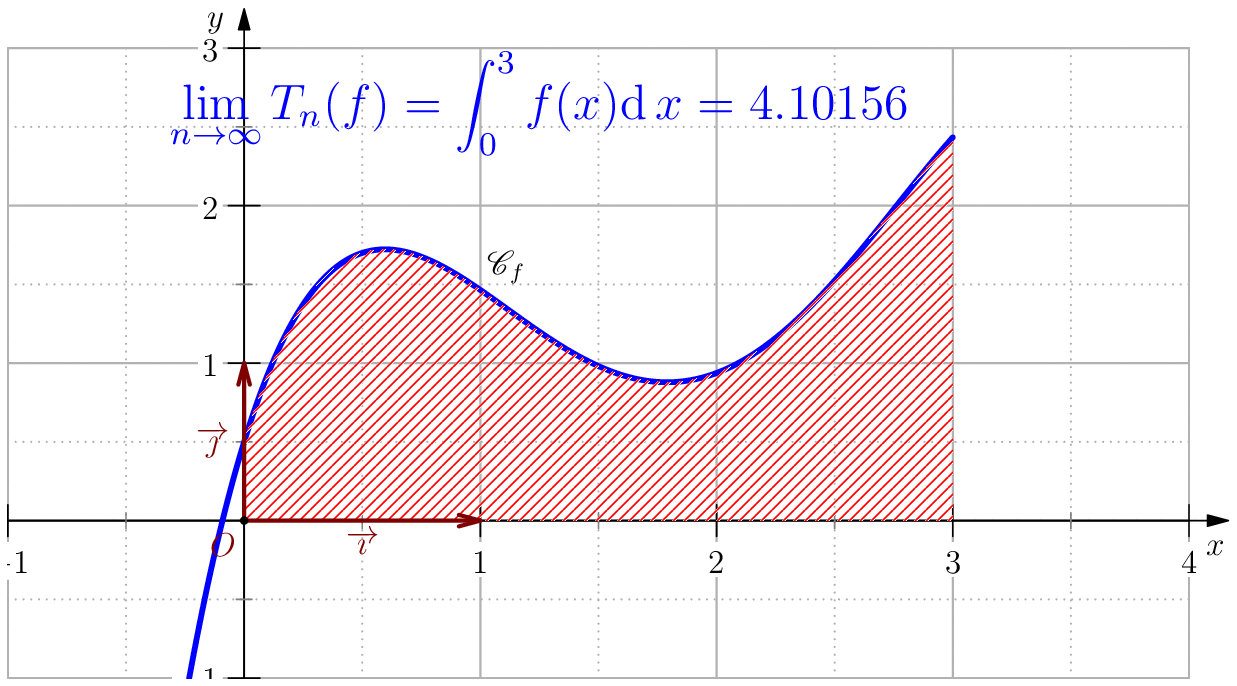
On pose $$f(x)=-\dfrac{85}{256}x^4+\dfrac{165}{64}x^3-\dfrac{197}{32}x^2+\dfrac{39}{8}x+\dfrac{1}{2}$$ alors, $$\dsp \int f(x)\ud x=-(17/256)x^5+(165/256)x^4-(197/96)x^3+(39/16)x^2+(1/2)x$$ En particulier, $$\int_0^3 f(x)\ud x= \dfrac{525}{128}=4.1015625$$
- Convergence de la méthode des trapèzes. (Animation en pdf)
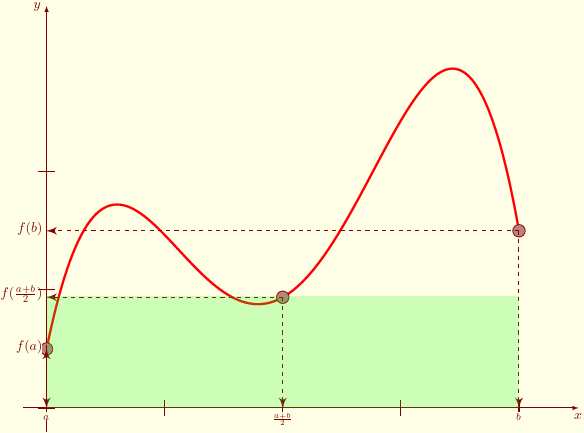
Méthode de Simpson
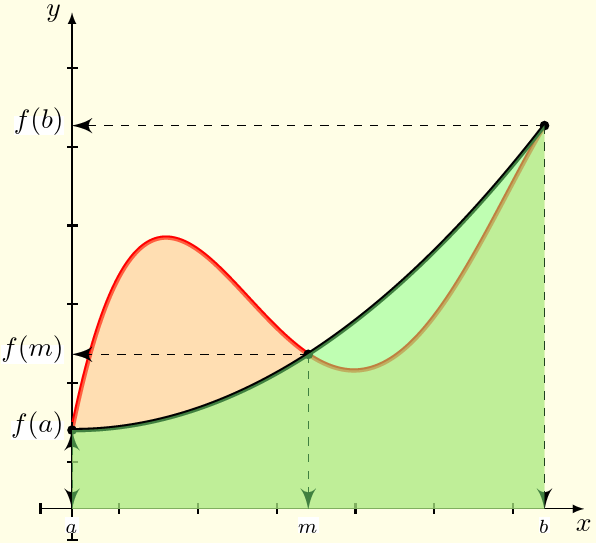
L'idée principale de cette méthode est d'approcher la fonction $f$ sur $[a,b]$ par une fonction polynomiale de degré 2 qui passe par les points $(a,f(a)),\,(m,f(m)),\,(b,f(b))$, avec $m=\dfrac{a+b}{2}$, i.e. $$\begin{array}{lcl} f(t)&\simeq& f(a)\dfrac{(t-m)(t-b)}{(a-m)(a-b)}\\ &&+f(m)\dfrac{(t-a)(t-b)}{(m-a)(m-b)}+f(b)\dfrac{(t-a)(t-m)}{(b-a)(b-m)}. \end{array} $$ Ainsi, après calculs, $$\boxed{\int_a^bf(t)\ud t\simeq\dfrac{b-a}{6}\left( f(a)+4f(m)+f(b)\right)}.$$
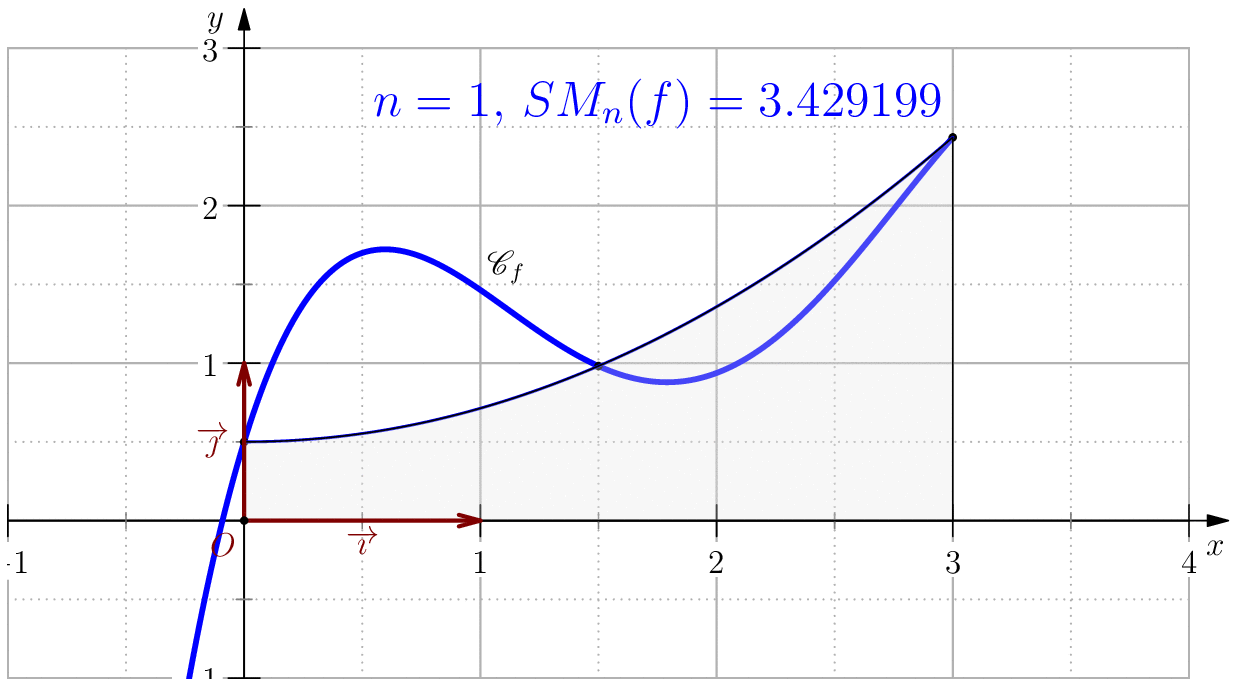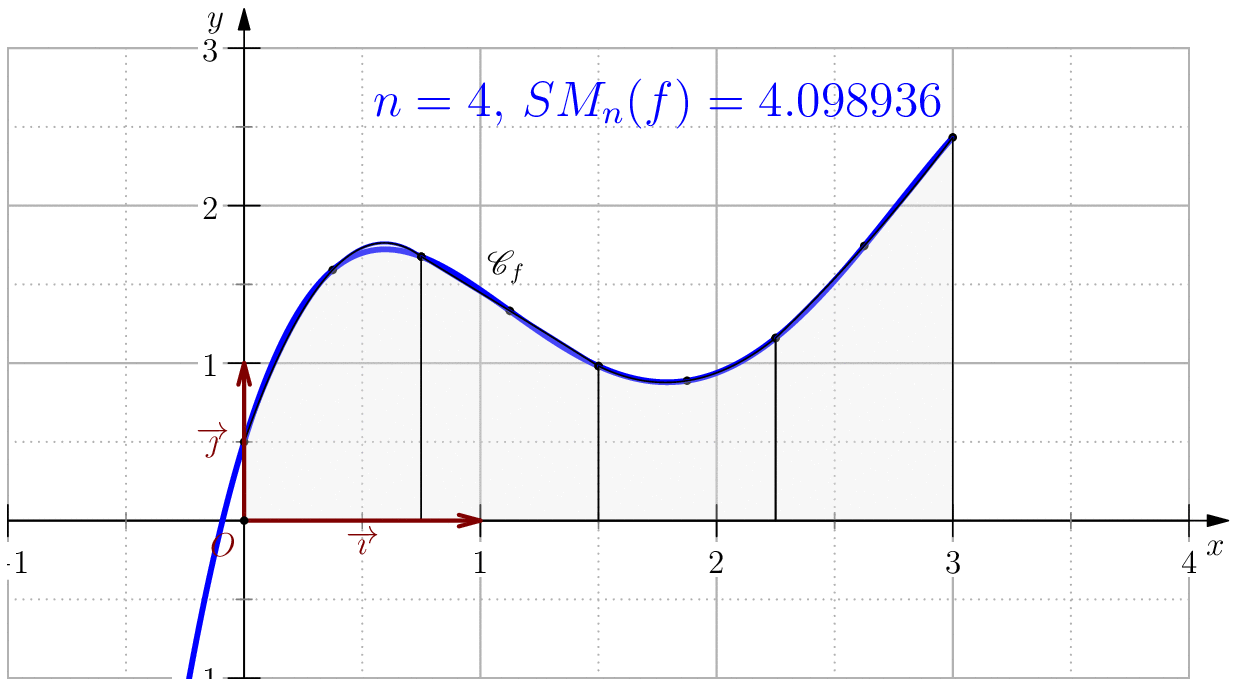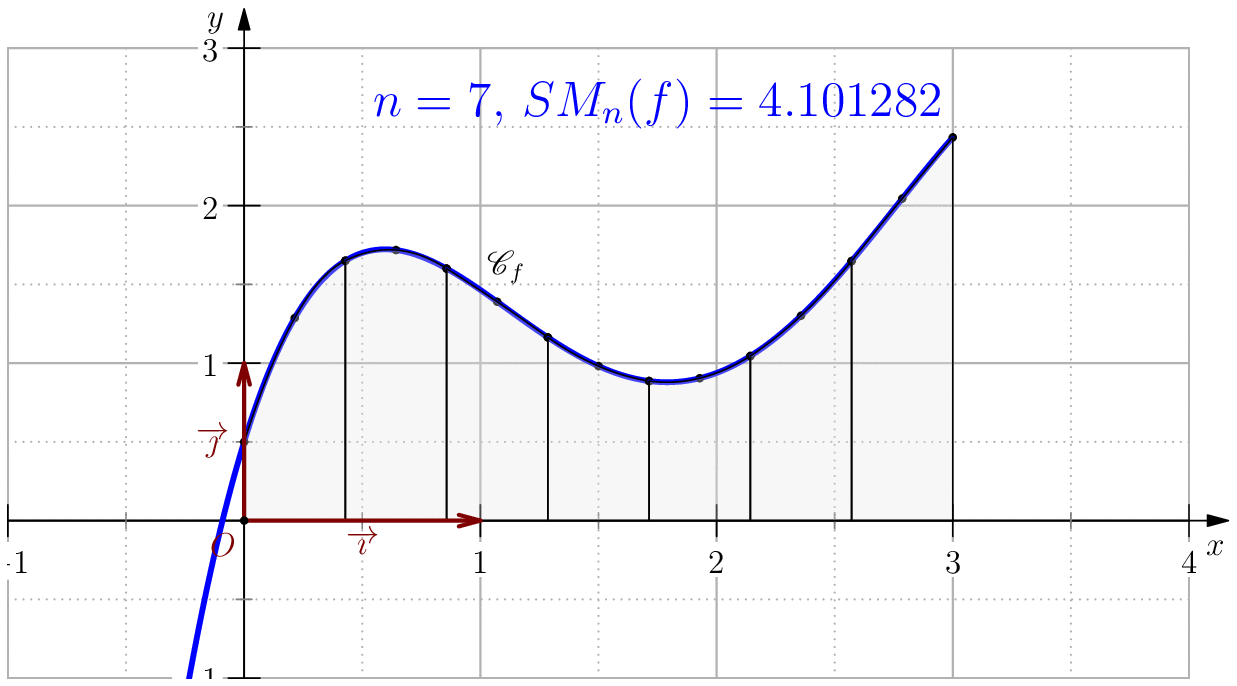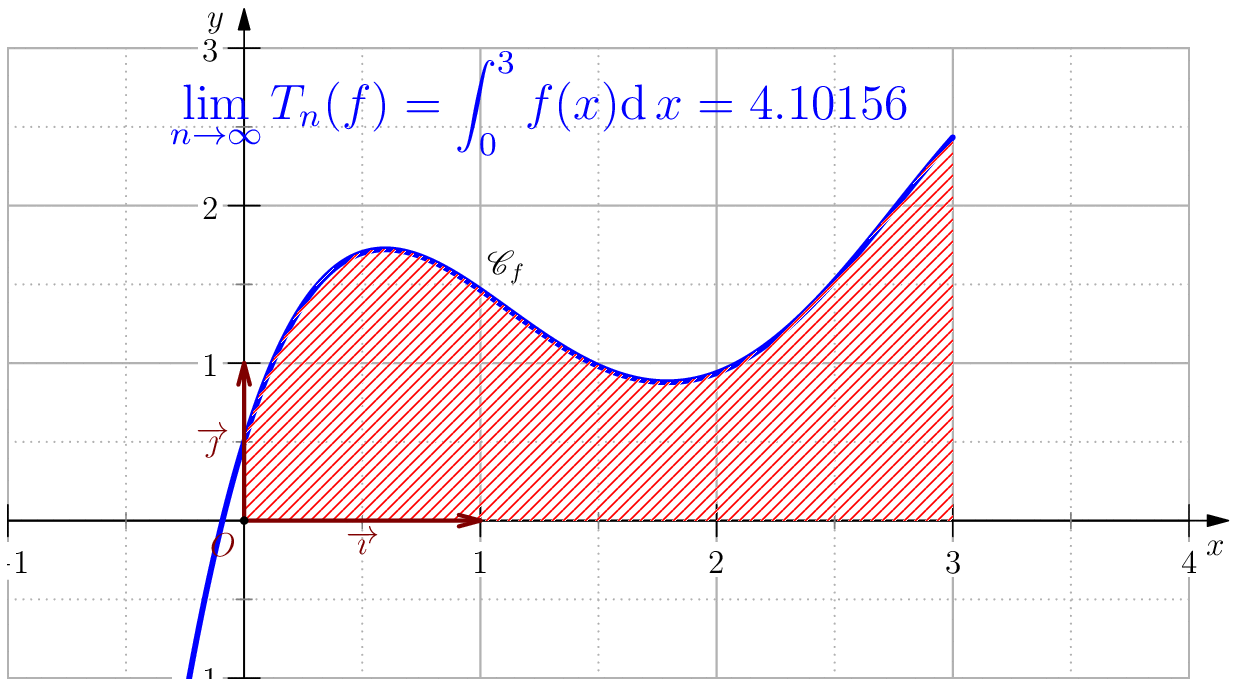
Pour $n\in \N$, on note $S_n(f)=\dfrac{b-a}{6n}\dsum_{k=0}^{n-1}\left(f(a_k)+4f(\frac{a_k+a_{k+1}}{2})+f(a_{k+1})\right) $.
On suppose que $f\in \CC^4([a,b])$ alors: $$\boxed{\forall n\in \N^*,\quad\abs{\int_a^bf(t)\ud t-S_n(f)}\leq \dfrac{(b-a)^5}{2880n^4}\norme{f^{(4)}}_\infty}.$$
On pose $$f(x)=-\dfrac{85}{256}x^4+\dfrac{165}{64}x^3-\dfrac{197}{32}x^2+\dfrac{39}{8}x+\dfrac{1}{2}$$ alors, $$\dsp \int f(x)\ud x=-(17/256)x^5+(165/256)x^4-(197/96)x^3+(39/16)x^2+(1/2)x$$ En particulier, $$\int_0^3 f(x)\ud x= \dfrac{525}{128}=4.1015625$$
- Convergence de la méthode de Simpson. (Animation en pdf)