Suites et séries de fonctions
Suites de fontions
Étudier les suites d'applications suivantes (CS, CU):
- $f_n:\R\mapsto \R,~~f_n(x)=\dfrac{nx}{1+n^2x^2}$
- $f_n:\R\mapsto \R,~~f_n(x)=\dfrac{nx^3}{1+nx^2}$
- $f_n:\R_+\mapsto \R,~~f_n(x)=\dfrac{x^n-1}{x^n+1}$
- $f_n:\R_+\mapsto \R,~~f_n(x)=\ln\left(1+\dfrac{x}{n}\right)$
- $f_n:\R_+^*\mapsto \R,~~f_n(x) =\dfrac{nx^2\ee^{-nx}}{(1-\ee^{-x})^2} $
- $n\in\N^*,~~f_n:\R\mapsto \R,~~f_n(x)=\min\left( n,\dfrac{x^2}{n}\right)$
- $f_n:\R\mapsto \R,~~f_n(x)=\left\{ \begin{array}{ll} 0 & \textrm{ si } \ 0 \leqslant x \leqslant 1/ n \\ \dfrac{1}{n \ln \left( 1 - \frac{1}{nx}\right)} & \textrm{ si } \ x < 0 \textrm{ ou } x >1/n \end{array} \right.$
- $f_n:\R_+\mapsto \R,~~f_n(x)=\sin\left(\sqrt{x+4\pi^2n^2}\right)-\dfrac{x}{4\pi n}$
-
$f_n:\R\mapsto \R,~~f_n(x)=\dfrac{nx}{1+n^2x^2}$.
Pour tout $x\in\R$, on a $ \dfrac{nx}{1+n^2x^2}\tendvers{n}{\infty}0$, donc $\boxed{f_n\overset{CS}{\tendvers{n}{\infty}}0}$. En revanche, pour $n>0$, on a $f\left(\frac{1}{n}\right)=\frac{1}{2}$, donc $f_n$ ne converge pas uniformément vers $0$ sur $\R$.
Pour $a>0$, on a $$\forall x\in \R,~~\abs{x}\leq a \Longrightarrow \abs{f_n(x)}=\dfrac{n\abs{x}}{1+n^2x^2}\leq \dfrac{1}{n\abs{x}}\leq \dfrac{1}{na}.$$ On en déduit $f_n\overset{CU}{\tendvers{n}{\infty}}0$ sur $]-\infty,-a[\cup ]a,\infty[$.
$\,$
Fixer d'abord $x_0$ puis faites varier $n$ (convergence simple)
Ensuite, faites varier $x_0$
-
$f_n:\R\mapsto \R,~~f_n(x)=\dfrac{nx^3}{1+nx^2}$.
Pour tout $x\in\R$, on a $ \dfrac{nx^3}{1+nx^2}\tendvers{n}{\infty}x$, donc $\boxed{f_n\overset{CS}{\tendvers{n}{\infty}}f}$ avec $f(x)=x$.
Notons $g_n=f_n-f$, on a $$\forall x\in \R,~~g_n(x)=\dfrac{-x}{1+nx^2},~~~~ g_n'(x)=\dfrac{-1+nx^2}{(1+nx^2)^2}.$$ Donc $\norme{g_n}_\infty\leq \dfrac{1}{2\sqrt{n}}\tendvers{n}{\infty}0$. On en déduit $\boxed{f_n\overset{CU}{\tendvers{n}{\infty}}f}$.$\,$
$\,$
Fixer d'abord $x_0$ puis faites varier $n$ (convergence simple)
Ensuite, faites varier $x_0$
-
$f_n:\R_+\mapsto \R,~~f_n(x)=\dfrac{x^n-1}{x^n+1}$.
On distingue 3 cas:- Si $x\in [0,1[$ alors $x^n\tendvers{n}{\infty}0$ donc $f_n(x)\tendvers{n}{\infty}-1$.
- Si $x=1$ alors $x^n=1$ donc $f_n(1)=0\tendvers{n}{\infty}0$.
- Si $x\in ]1,\infty[$ alors $x^n\tendvers{n}{\infty}\infty$ donc $f_n(x)\tendvers{n}{\infty}1$.
la convergence n'est pas uniforme car $f_n$ sont continues tandis que $f$ ne l'est pas. - $f_n:\R_+\mapsto \R,~~f_n(x)=\ln\left(1+\dfrac{x}{n}\right)$.
Pour tout $x\in \R_+$, on a $f_n(x)\underset{n\infty}{\thicksim}\dfrac{x}{n}$ donc $f_n(x)\tendvers{n}{\infty}0$. On en déduit que $\boxed{f_n\overset{CS}{\tendvers{n}{\infty}}0}$, d'autre part on a $f_n(n)=\ln(2)$ donc la convergence n'est pas uniforme sur $\R_+$.
En revanche, pour tout $b>0$, on a $\norme{f_n}_\infty^{[0,b]}=\ln\left(1+\dfrac{b}{n}\right)\tendvers{n}{\infty}0$, donc $\boxed{f_n\overset{CU}{\tendvers{n}{\infty}}0}$ sur $[0,b]$. - $f_n:\R_+^*\mapsto \R,~~f_n(x) =
\dfrac{nx^2\ee^{-nx}}{(1-\ee^{-x})^2} $.
Pour tout $x>0$, on a $nx^2\ee^{-nx}\tendvers{n}{\infty}0$ donc $\limiteX{n}{\infty}f_n(x)=0$. On en déduit que $\boxed{f_n\overset{CS}{\tendvers{n}{\infty}}0}$.
D'autre part, on a $f_n(x)\underset{x\rightarrow 0^+}{=}n+\mathrm{o}(1)$, donc $\limiteX{x}{0^+}f_n(x)=n$ doncla convergence n'est pas uniforme sur $\R_+^*$ .
Soit $a>0$, on a: $$\forall x\in [a,\infty[,\,\abs{f_n(x)}\leq \dfrac{nx^2\ee^{-nx}}{(1-\ee^{-a})^2}\leq \dfrac{4\ee^{-2}}{(1-\ee^{-a})^2}\dfrac{1}{n}\Longrightarrow \norme{f_n}_\infty^{[a,\infty}\leq \dfrac{K}{n}\tendvers{n}{\infty}0,$$ donc $\boxed{f_n\overset{CU}{\tendvers{n}{\infty}}0}$ sur $[a,\infty[$. - $n\in\N^*,~~f_n:\R\mapsto \R,~~f_n(x)=\min\left( n,\dfrac{x^2}{n}\right)$.
La suite $(f_n)$ converge simplement sur $\R$ vers la fonction nulle. En effet:
Soit $x\in\R$ ,fixé. Il existe un entier $n_0$ tel que, pour tout $n\geq n_0$, on ait $\dfrac{x^2}{n}< n$ donc, pour $n\geq n_0$, $f_n(x)=\dfrac{x^2}{n}$ d'où $\dsp \lim_{n\to\infty}f_n(x)=0$.
Cependant,il n'y a pas convergence uniforme sur $\R$ , puisque $\dsp\sup_{x\in \R}\abs{f_n(x)-f(x)}=\dsp\sup_{x\in \R}f_n(x)=n$.
Il y a cependantconvergence uniforme sur tout segment $[-a,a]$ ($a>0$) . En effet, à partir d'un certain rang $n_0$, on a $\dfrac{a^2}{n}< n$, donc pour tout $x\in[-a,a]$, on aura, pour $n\geq n_0$, $f_n(x)=\dfrac{x^2}{n}$ et $\dsp\sup_{x\in[-a,a]}\abs{f_n(x)-f(x)}=\dfrac{a^2}{n}$, qui tend vers $0$ quand $n$ tend vers $+\infty$. - $f_n:\R\mapsto \R,~~f_n(x)=\left\{ \begin{array}{ll} 0 & \textrm{ si } \ 0 \leqslant x
\leqslant 1/ n \\
\dfrac{1}{n \ln \left( 1 - \frac{1}{nx}\right)} & \textrm{ si } \ x< 0 \textrm{ ou } x >1/n
\end{array} \right.$.
Il faut noter d'abord que $f_n$ est bien définie sur $\R$, en effet $1-\frac{1}{nx}>0$ (et $\neq 1$) ssi $x\in\R\setminus [0,1/n]$ .
Soit $x\in \R^*$, si $x>0$ il existe alors $n_0\in \N$ tel que $x>\frac{1}{n_0}$, donc pour $n\geq n_0$ on a $f_n(x)=\dfrac{1}{n \ln \left( 1 - \frac{1}{nx}\right)}$.
Comme $n\ln\left(1-\frac{1}{nx}\right)\underset{n\rightarrow\infty}{\thicksim}\frac{-1}{x}$, on en déduit que $f_n(x)\tendvers{n}{\infty}-x$, le résultat reste vraie pour $x=0$. On conclut $\boxed{ f_n\overset{CS}{\tendvers{n}{\infty}}f}$ avec $f(x)=-x$.
- Soit $n\in \N^*$, on a:
- Si $x\in [0,1/n]$ alors $\abs{f_n(x)-f(x)}=\abs{x}\leq \dfrac{1}{n}$.
- Si $x\in \R\setminus [0,1/n]$, alors $$\abs{f_n(x)-f(x)}=\abs{\dfrac{1}{n}\dfrac{1}{\ln(1-\frac{1}{nx})}-\dfrac{1}{n}\dfrac{1}{\frac{-1}{nx}}}=\dfrac{1}{n}\abs{\dfrac{1}{\ln(1-\frac{1}{nx})}-\dfrac{1}{\frac{-1}{nx}}}=\dfrac{1}{n}\abs{g(nx)}\leq \dfrac{1}{n}$$ avec $\fonct{g}{]-1,\infty[}{\R}{y}{\dfrac{1}{\ln(1+y)}-\dfrac{1}{y}}$, une étude rapide de $g$ montre qu'elle bornée ( On montre facilement que $\dsp\limiteX{x}{(-1)^+}g(x)=1,\,\dsp\limiteX{x}{0}g(x)=\frac{1}{2}$ et $\dsp\limiteX{x}{\infty}g(x)=0$).
- $f_n:\R_+\mapsto \R,~~f_n(x)=\sin(\sqrt{x+4\pi^2n^2})-\dfrac{x}{4\pi n}$.
Soit $x\geq 0$, on a $$f_n(x)=\sin\left(2\pi n\sqrt{1+\frac{x}{4\pi^2 n^2}}\right)-\frac{x}{4\pi n}=\sin \left(2\pi n+\frac{x}{4\pi n}+\mathrm{o}(1/n)\right)-\frac{x}{4\pi n}=\mathrm{o}(1/n)\tendvers{n}{\infty}0.$$ Donc $\boxed{ f_n\overset{CU}{\tendvers{n}{\infty}}0}$, cette convergence n'est pas uniforme (calculer $f(12\pi^2 n^2)$).
Pour $a>0$, $ \boxed{ f_n\overset{CU}{\tendvers{n}{\infty}}0}$ sur $[0,a]$ puisque $\norme{f_n}_\infty^{[0,a]}\leq \dfrac{a}{2\pi n}$.
Soient $I,J$ deux intervalles de $\R$, $\varphi: I\mapsto J$ , $\big(f_n:J\mapsto \R\big)_n$ une suites de fonctions, et $f:J\mapsto \R$. On suppose que $f_n\overset{C.U}{\longrightarrow}f$. Montrer que $f_n\circ\varphi \overset{C.U}{\longrightarrow}f\circ \varphi$.
Soit $\varepsilon>0$, comme $f_n\overset{C.U}{\longrightarrow}f$, alors:
$$\exists N\in \N,~~\forall n\geq N,~~\forall y\in J,~~\abs{f_n(y)-f(y)}\leq \varepsilon,$$
en particulière
(si on pose $y=\varphi(x)$), $\exists N\in \N,~~\forall n\geq N,~~\forall x\in I,~~
\abs{f_n(\varphi(x))-f(\varphi(x))}\leq \varepsilon,$
ce qui montre que $\boxed{f_n\circ\varphi\overset{C.U}{\longrightarrow}f\circ\varphi}$.
Soient $I$ un intervalle de $\R$, $\big(f_n:I\mapsto \R\big)_n$ une suites de fonctions,
$f:I\mapsto \R$ et $\varphi: \R\mapsto \R$ une fonction uniformément continue.i.e.
$$\forall \varepsilon >0,\,\,\exists \eta >0,\,\,\forall x,y\in \R,\quad \abs{x-y}\leq
\eta\Longrightarrow\abs{\varphi(x)-\varphi(y)}\leq \varepsilon.$$
On suppose que $f_n\overset{C.U}{\longrightarrow}f$. Montrer que $\varphi \circ f_n\overset{C.U}
{\longrightarrow}\varphi\circ f$.
Le résultat reste-t-il vrai si on remplace uniformément continue par continue pour $\varphi$?
Soit $\varepsilon>0$, comme $\varphi$ est uniformément continue, alors:
$$\exists \eta>0,~~\forall x,y\in \R,~~\big(\abs{x-y}\leq \eta\Longrightarrow\abs{\varphi(x)-
\varphi(y)}\leq \varepsilon\big).$$
D'autre part, puisque $f_n\overset{C.U}{\longrightarrow}f$,
$\exists N\in \N,~~\forall n\geq N,~~\big(\forall x\in I,~~\abs{f_n(x)-f(x)}\leq \eta\big)$.
Donc,
$$\forall n\geq N,~~\forall x\in I,~~\abs{\varphi(f_n(x))-\varphi(f(x))}\leq
\varepsilon\Longrightarrow\boxed{\varphi \circ f_n\overset{C.U}{\longrightarrow}\varphi\circ f}.$$
La condition de la continuité uniforme de $\varphi$ est indispensable, en effet le résultat devient
faux dans la cas contraire, comme le montre l'exemple suivant:
$$\dsp I=\R,~~f_n(x)=x+\frac{1}{n},~~\varphi(x)=x^2.$$
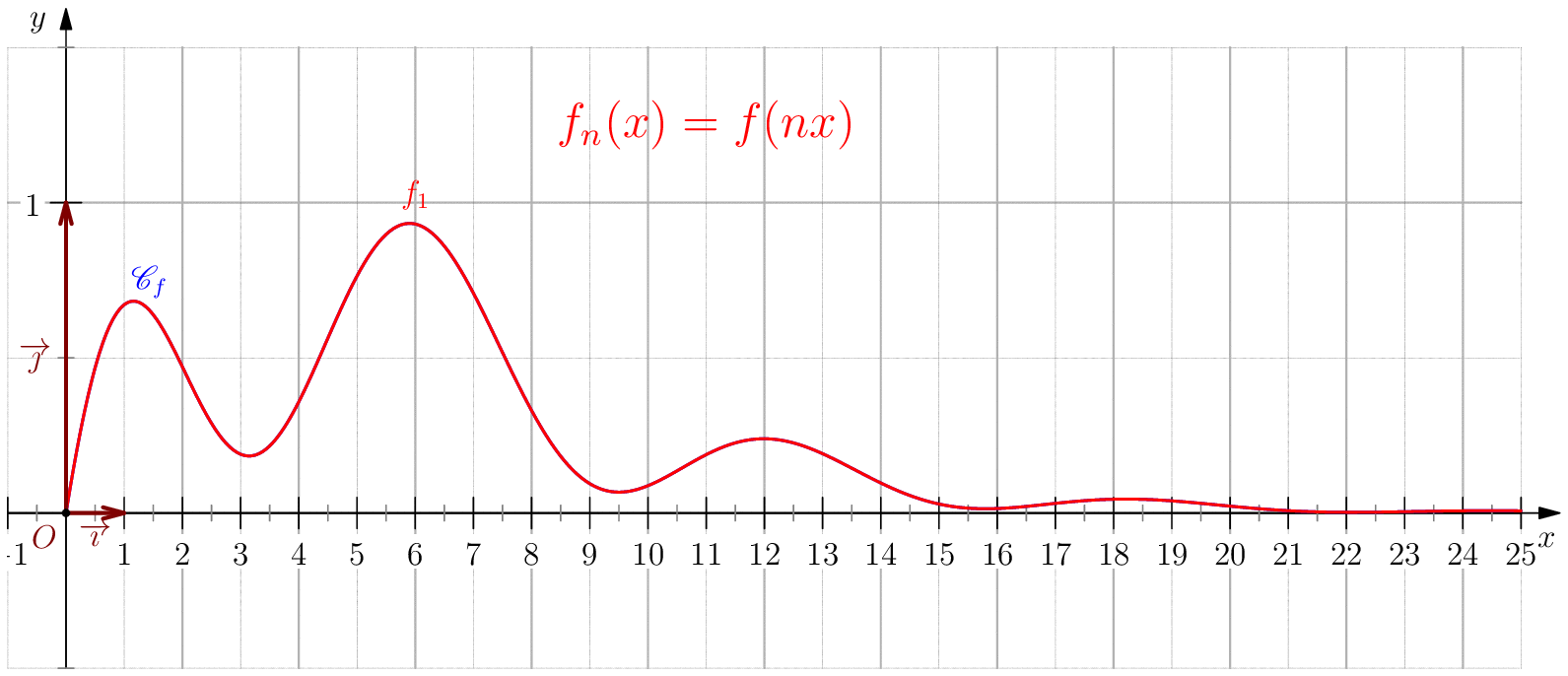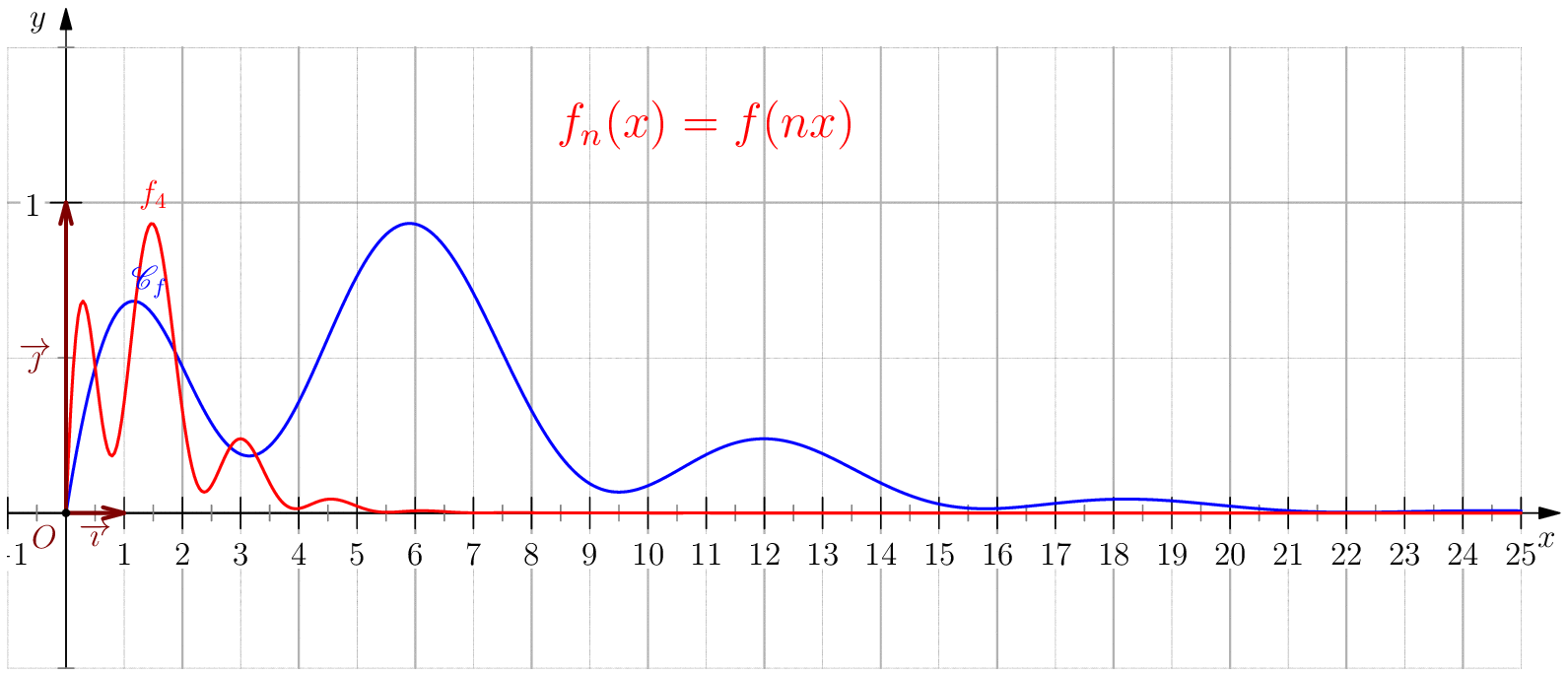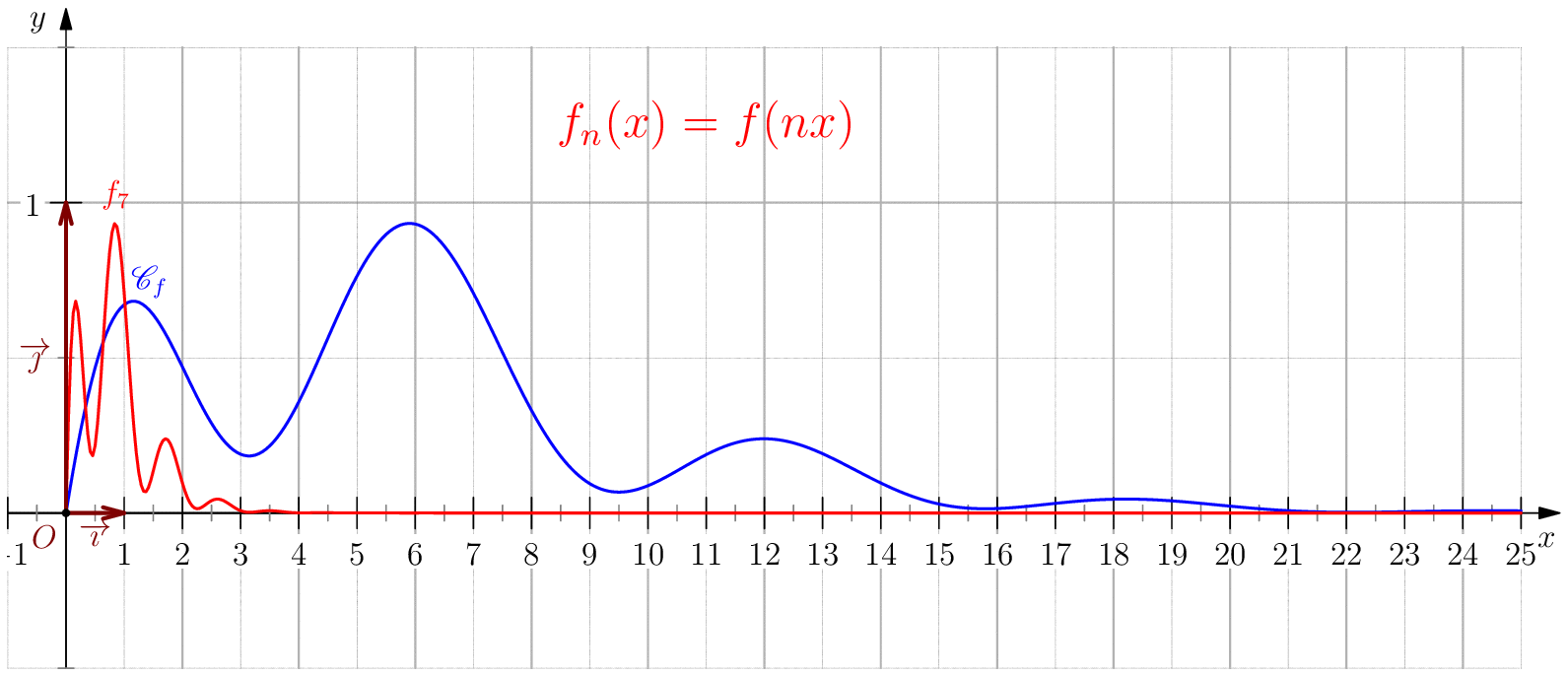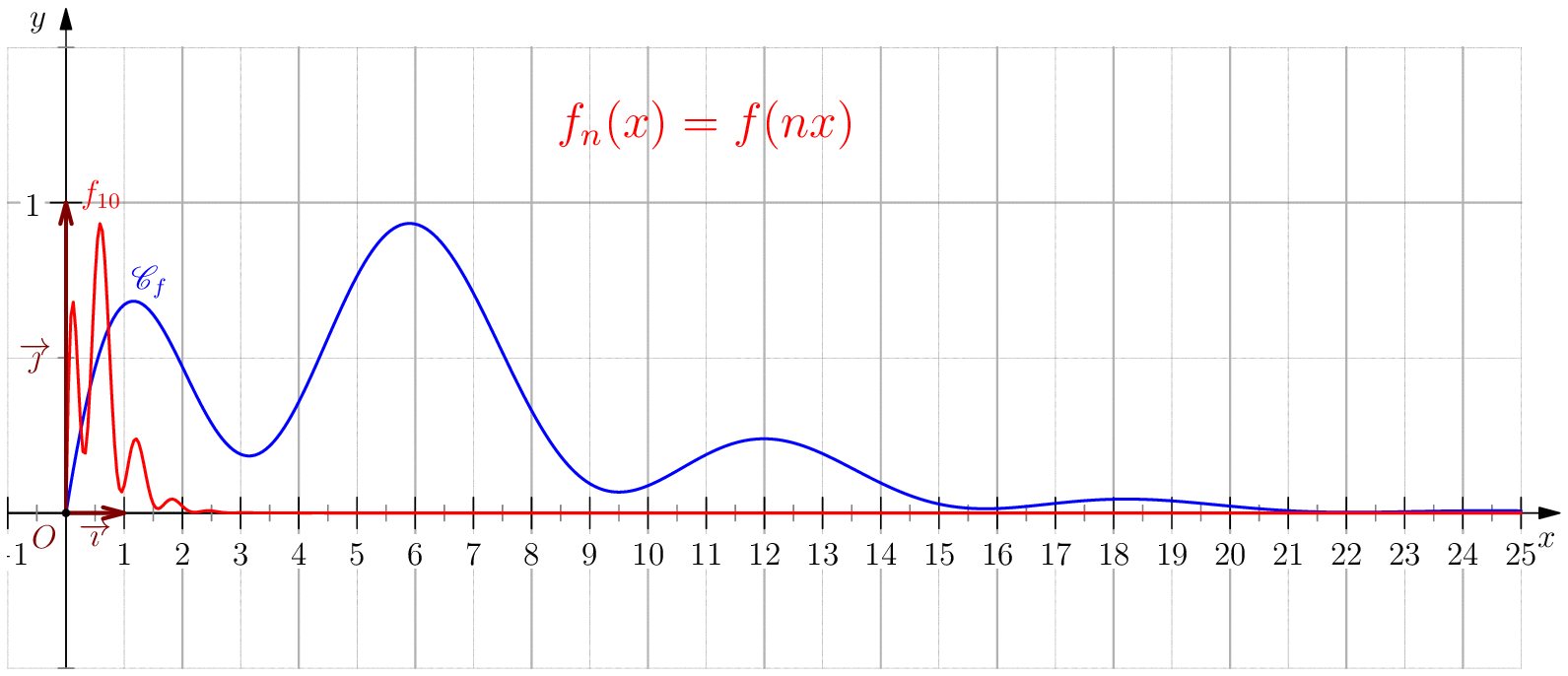
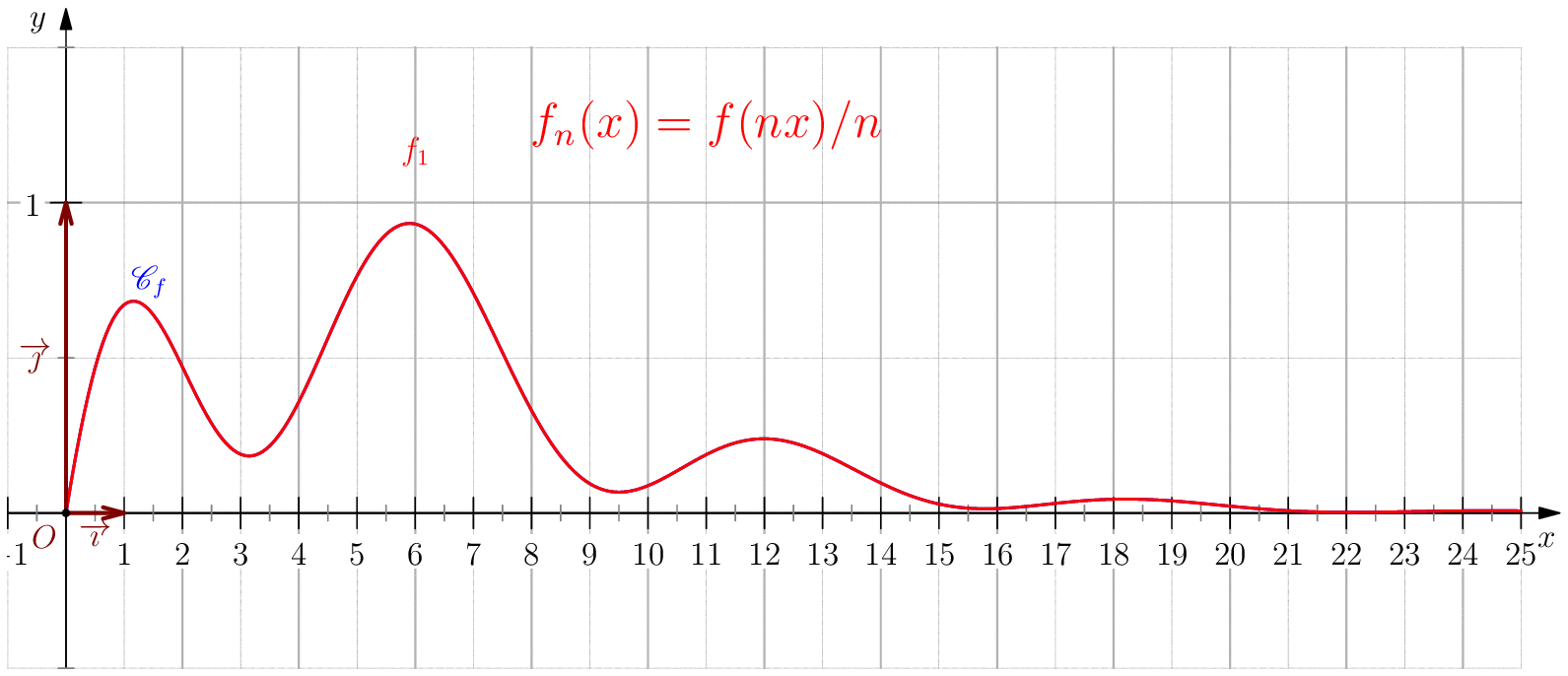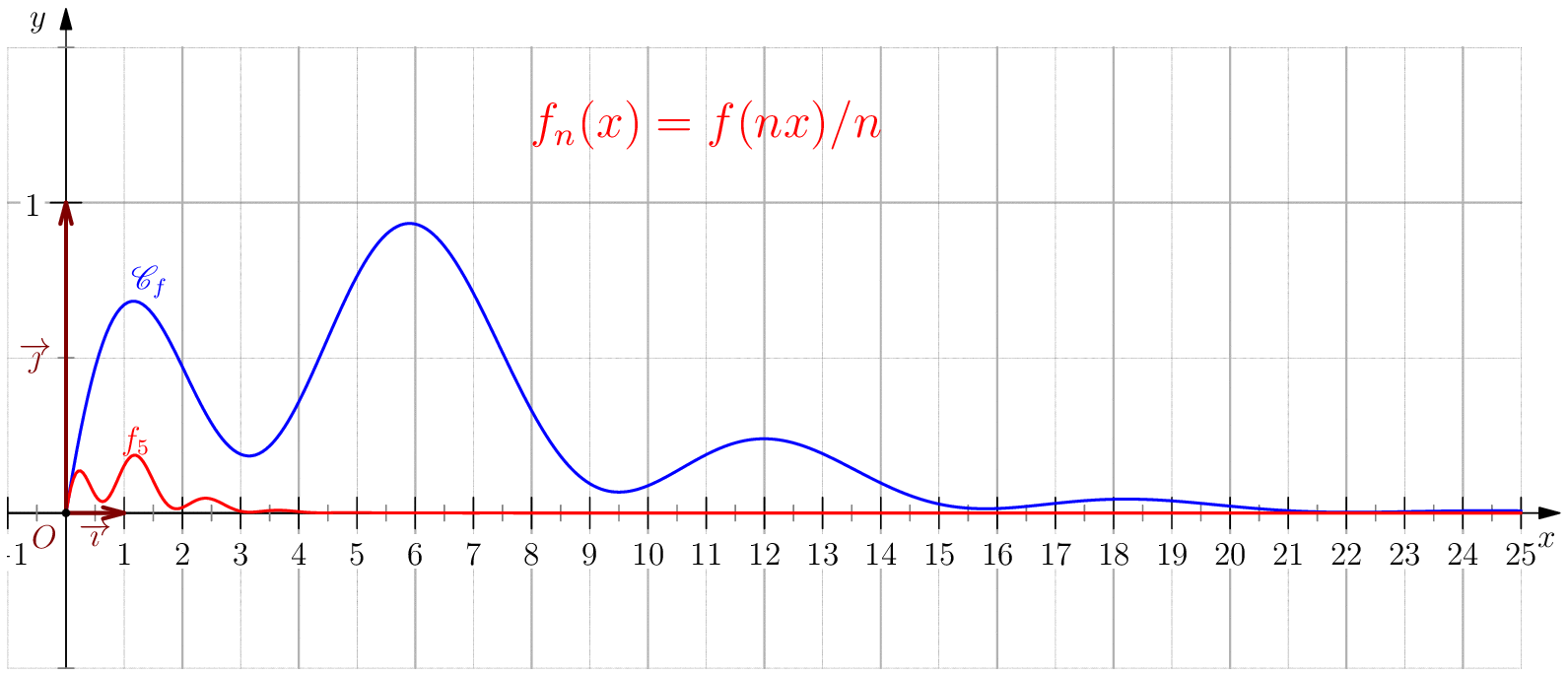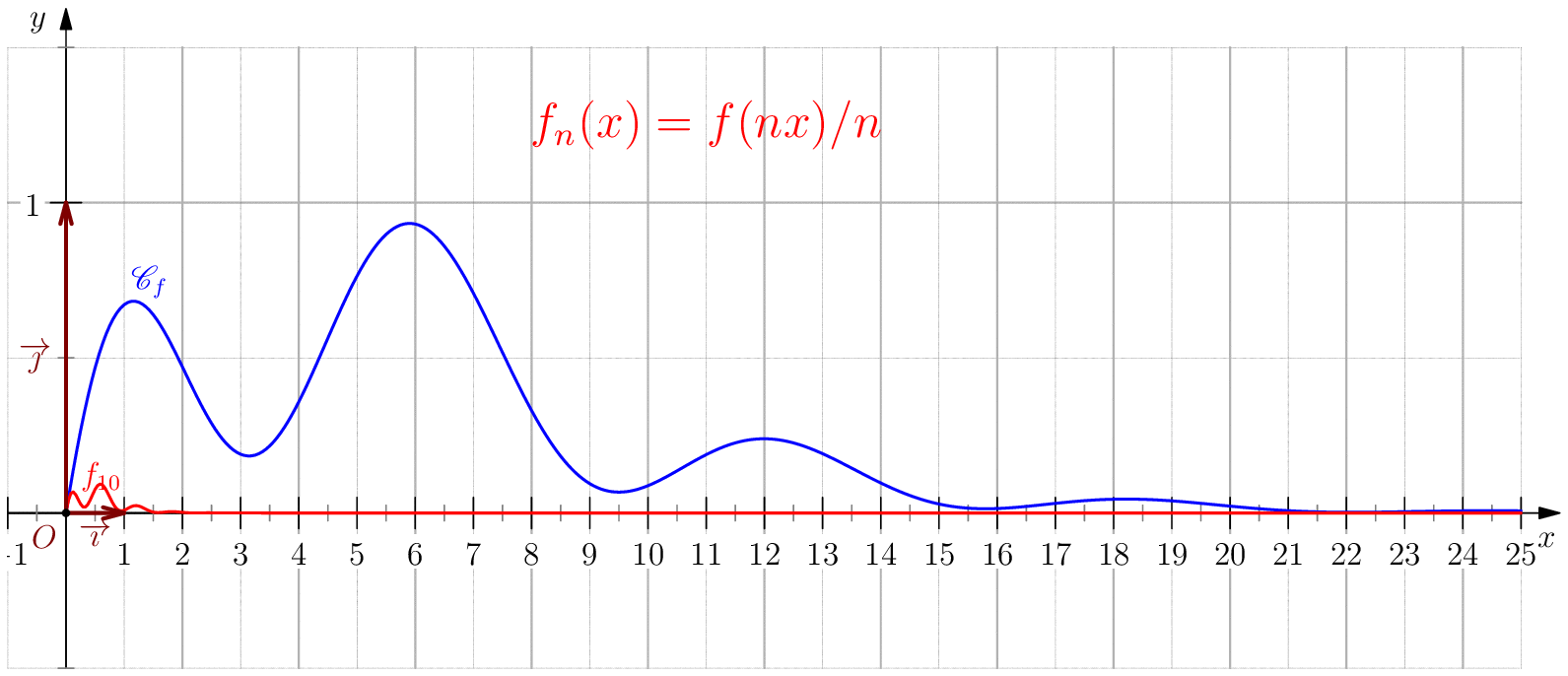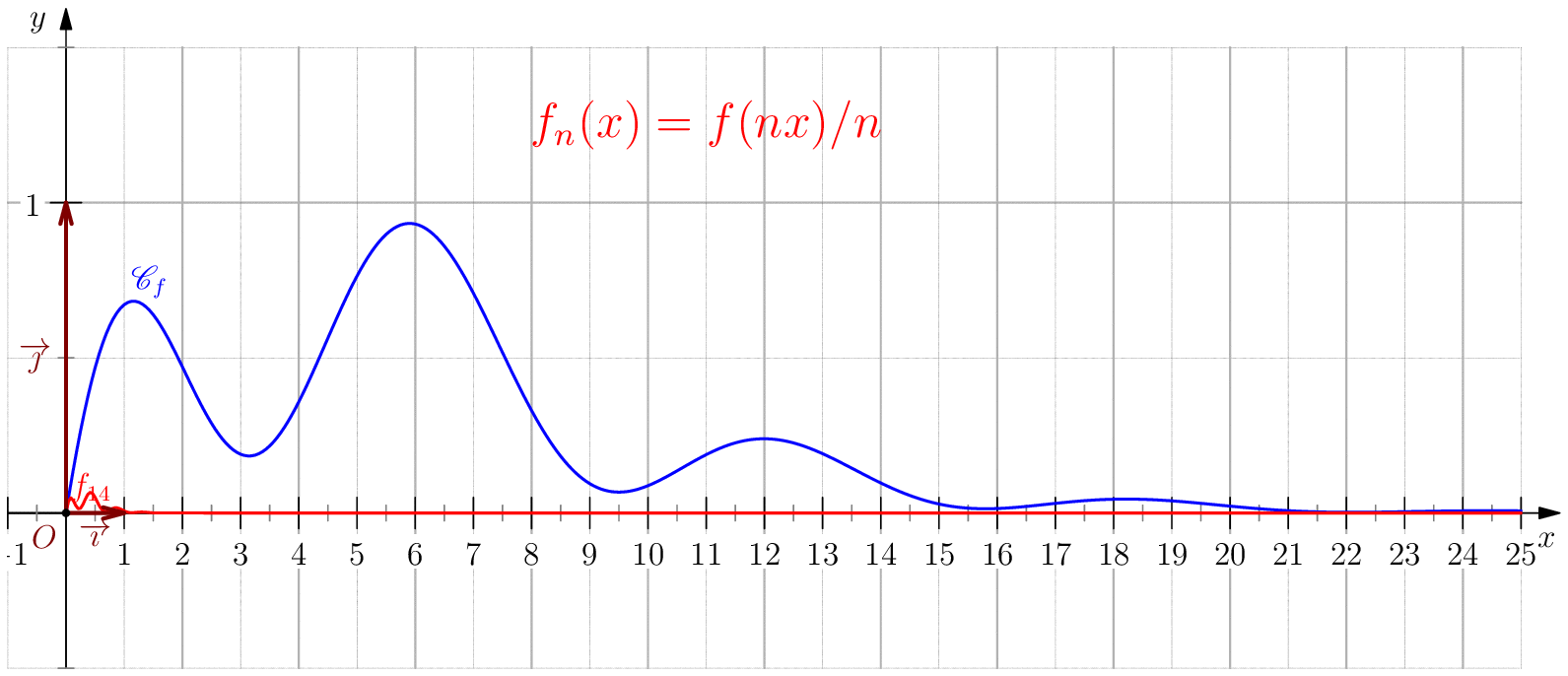
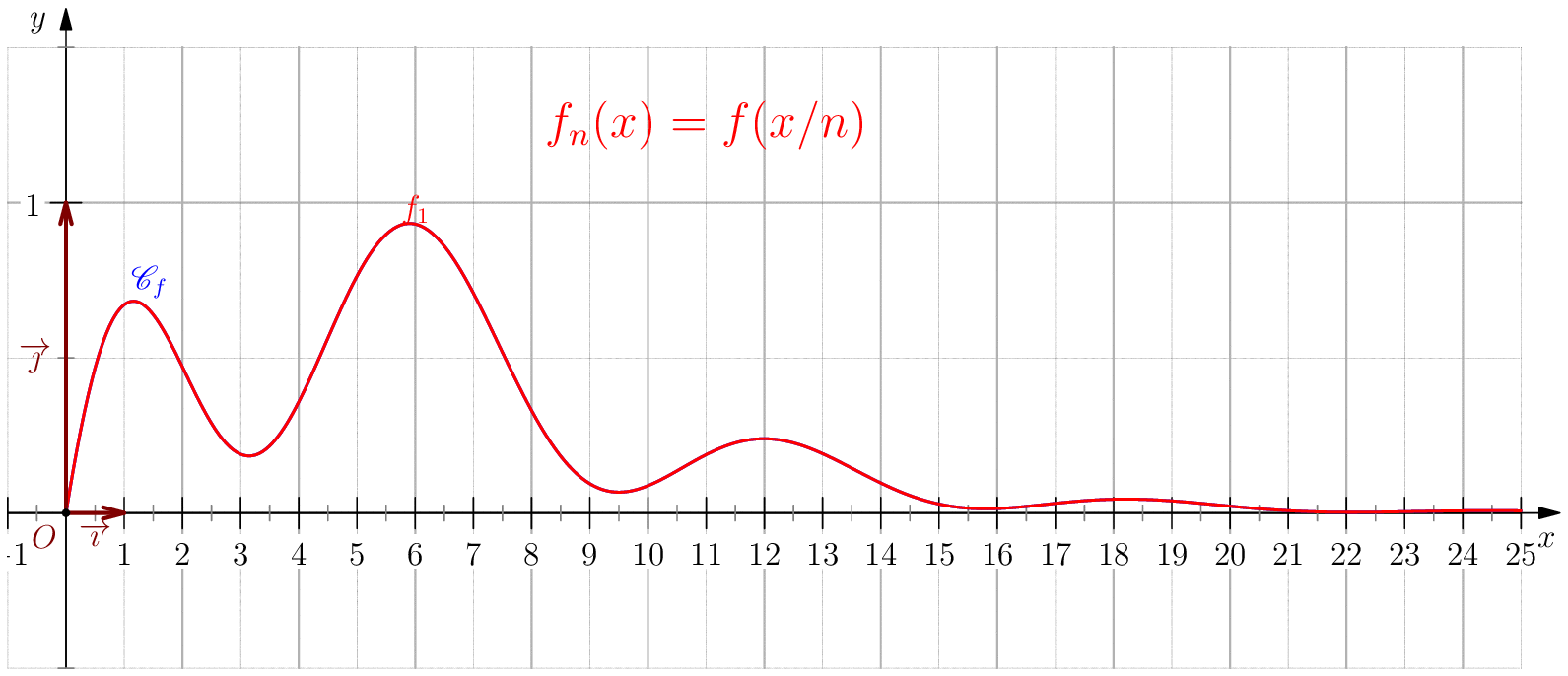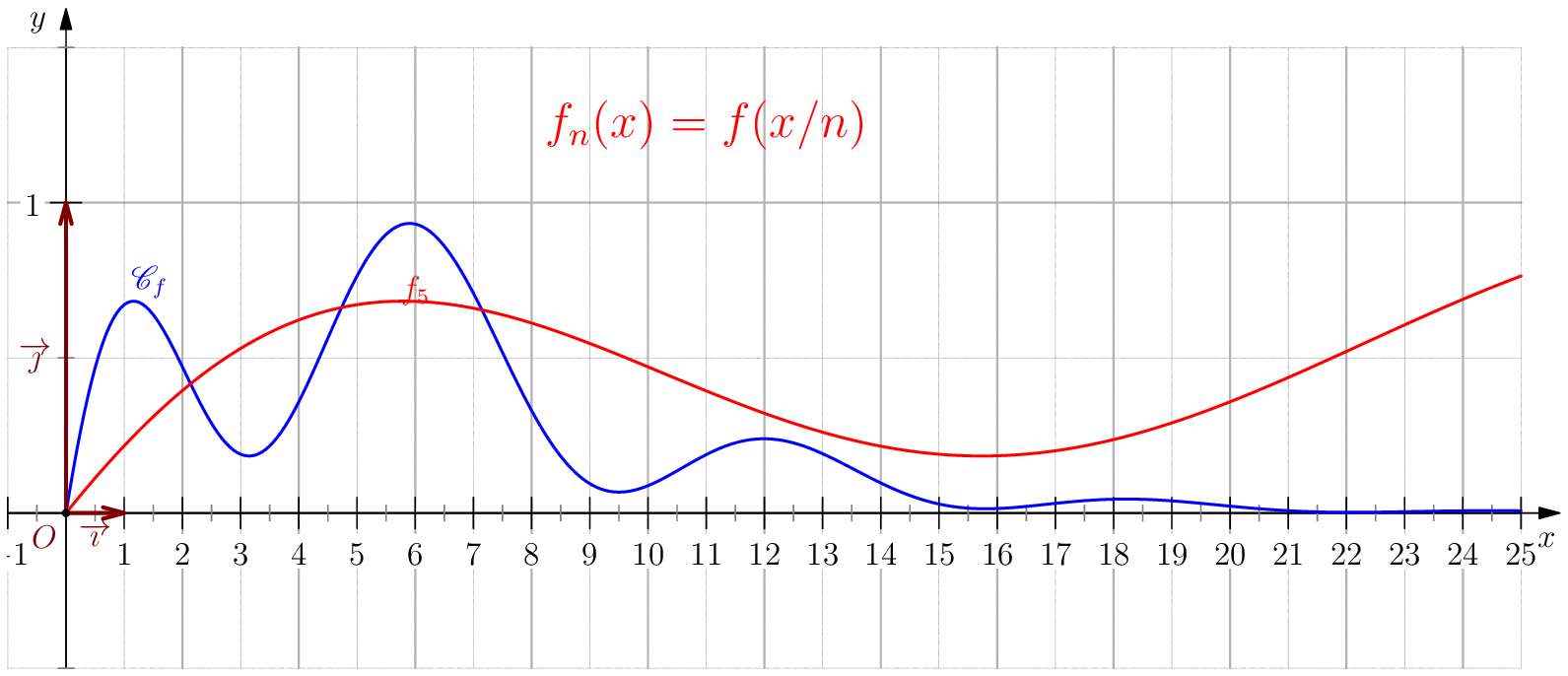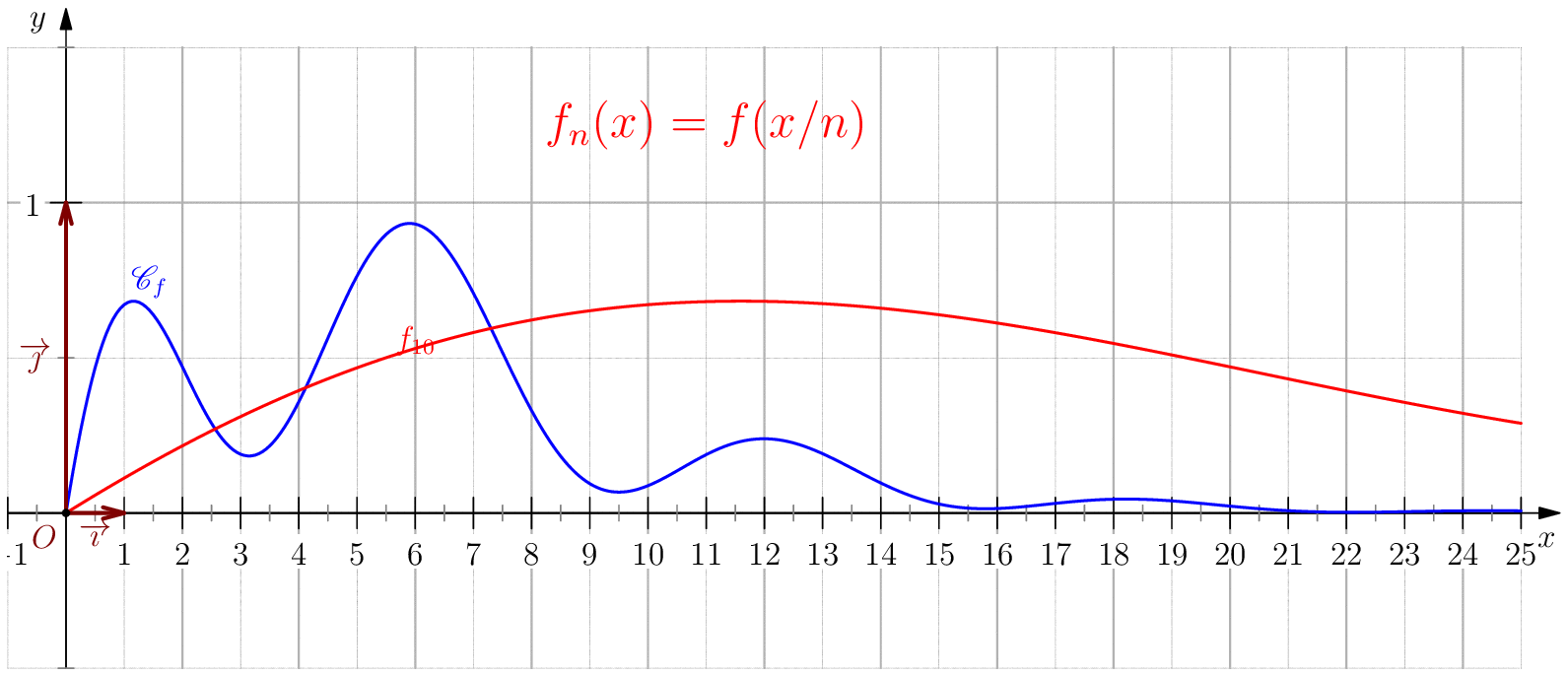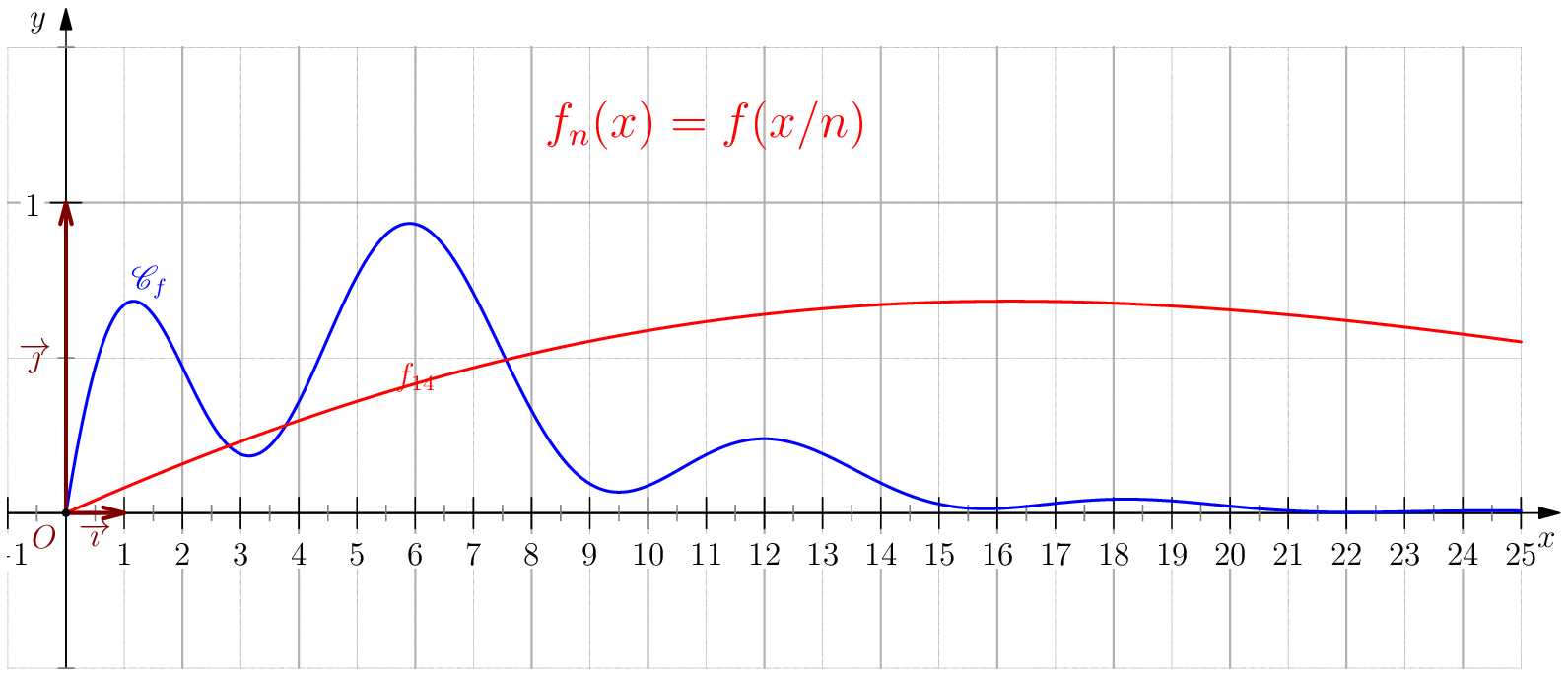
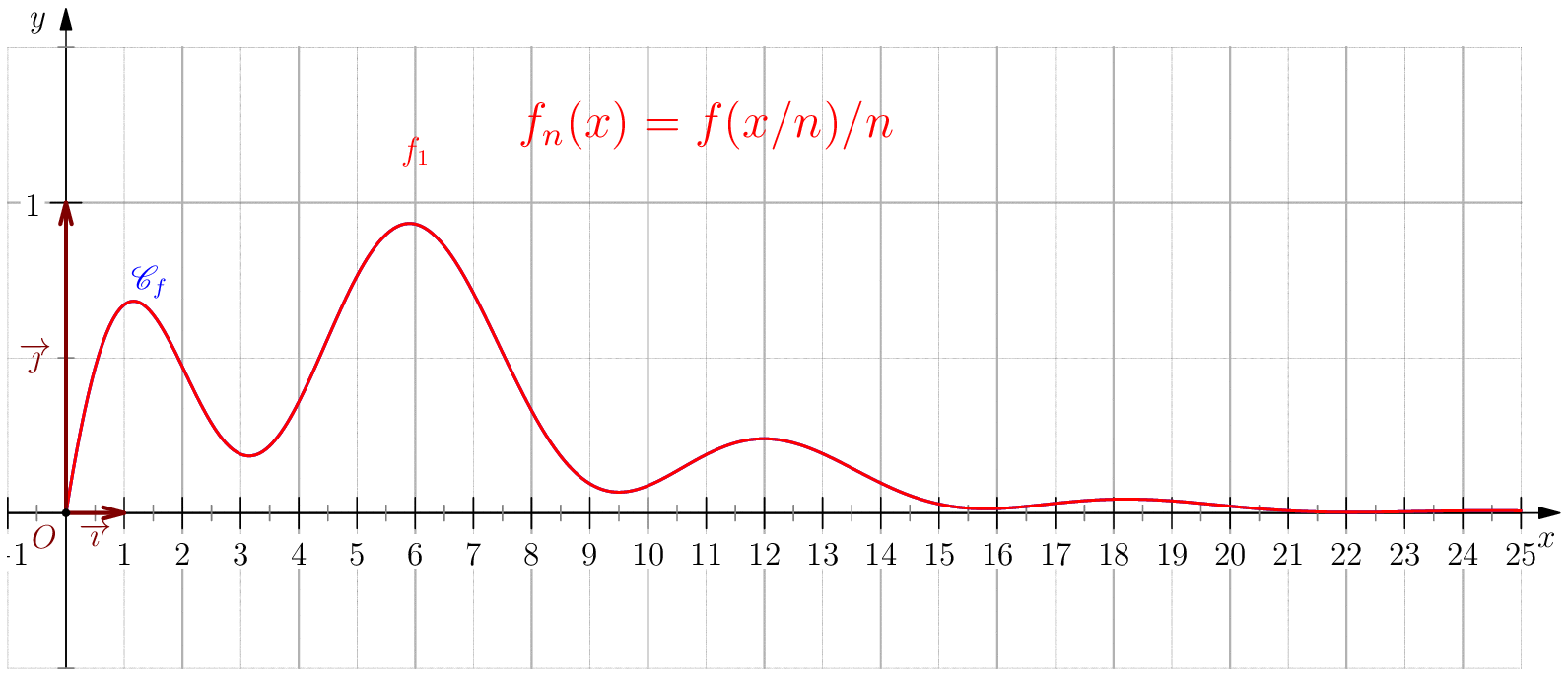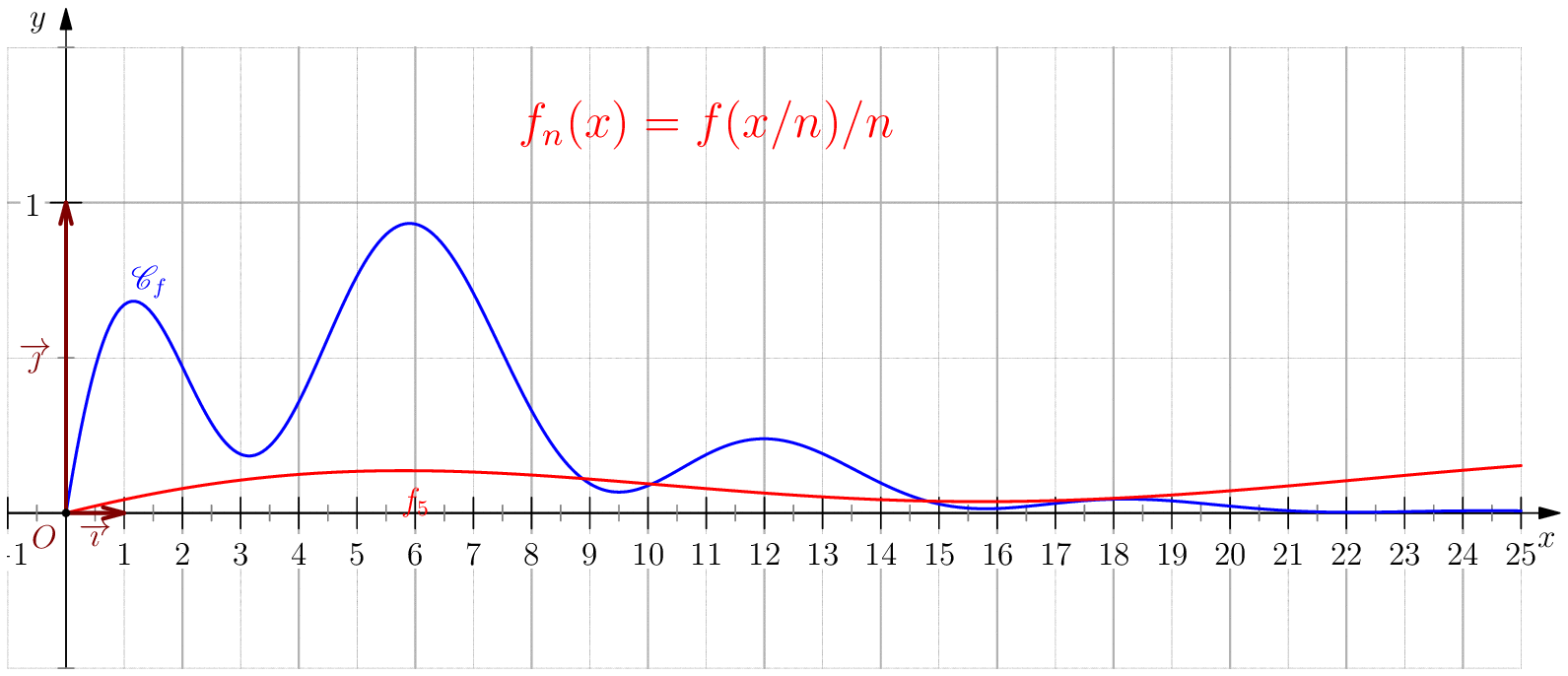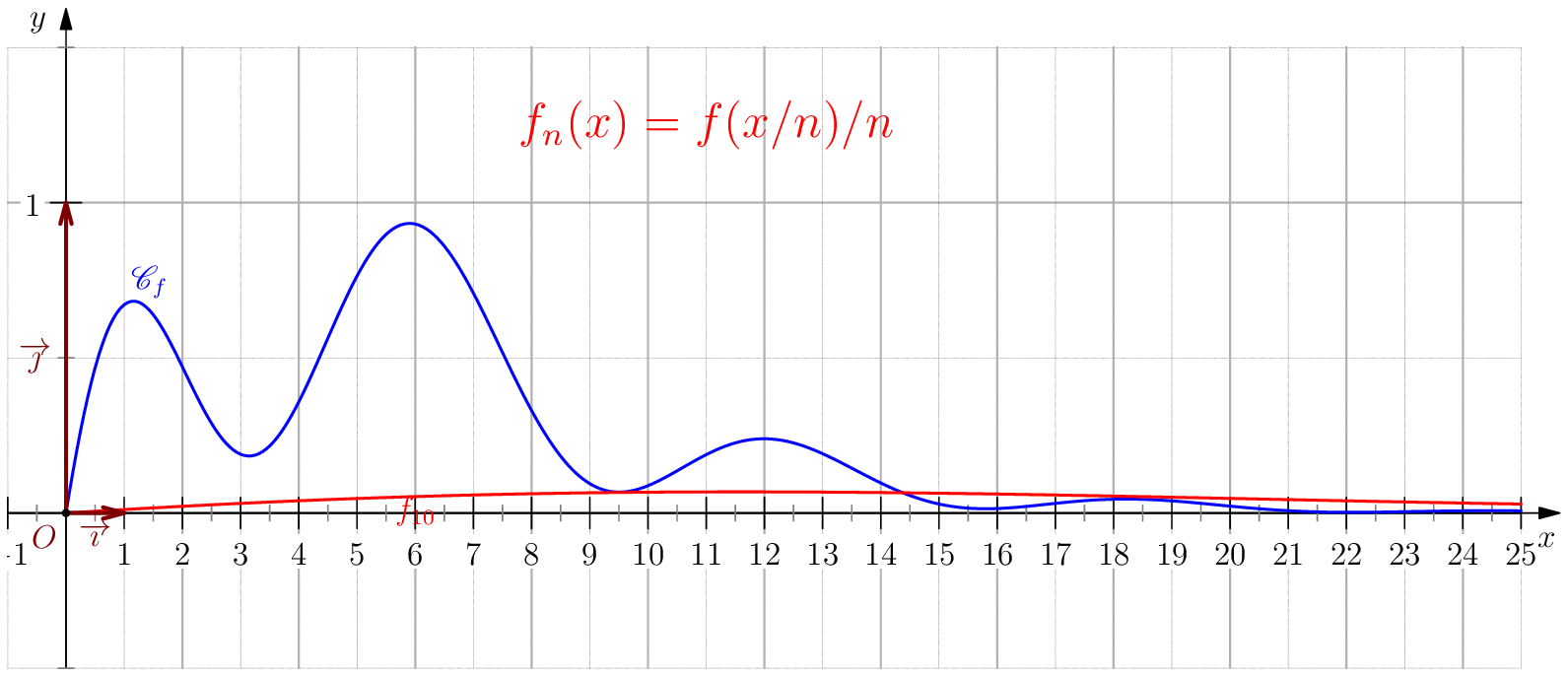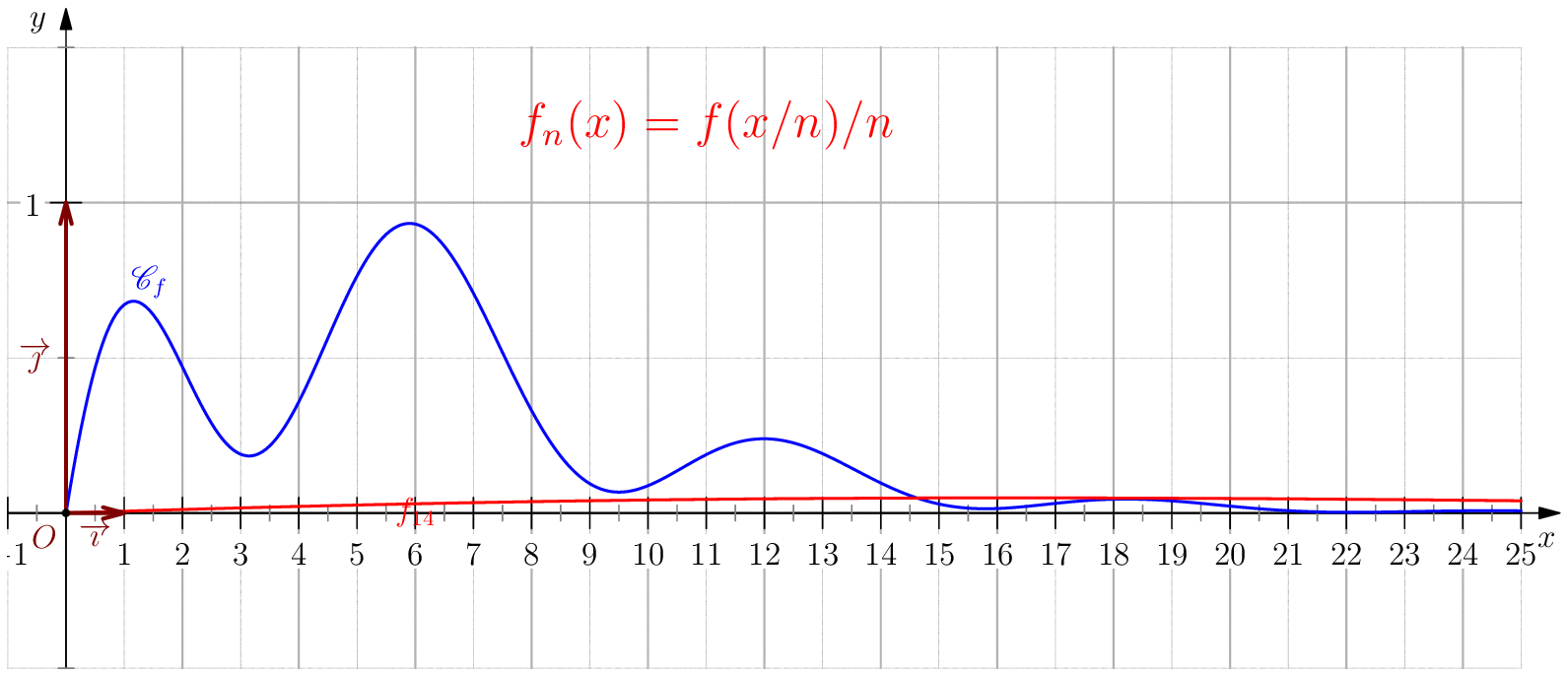
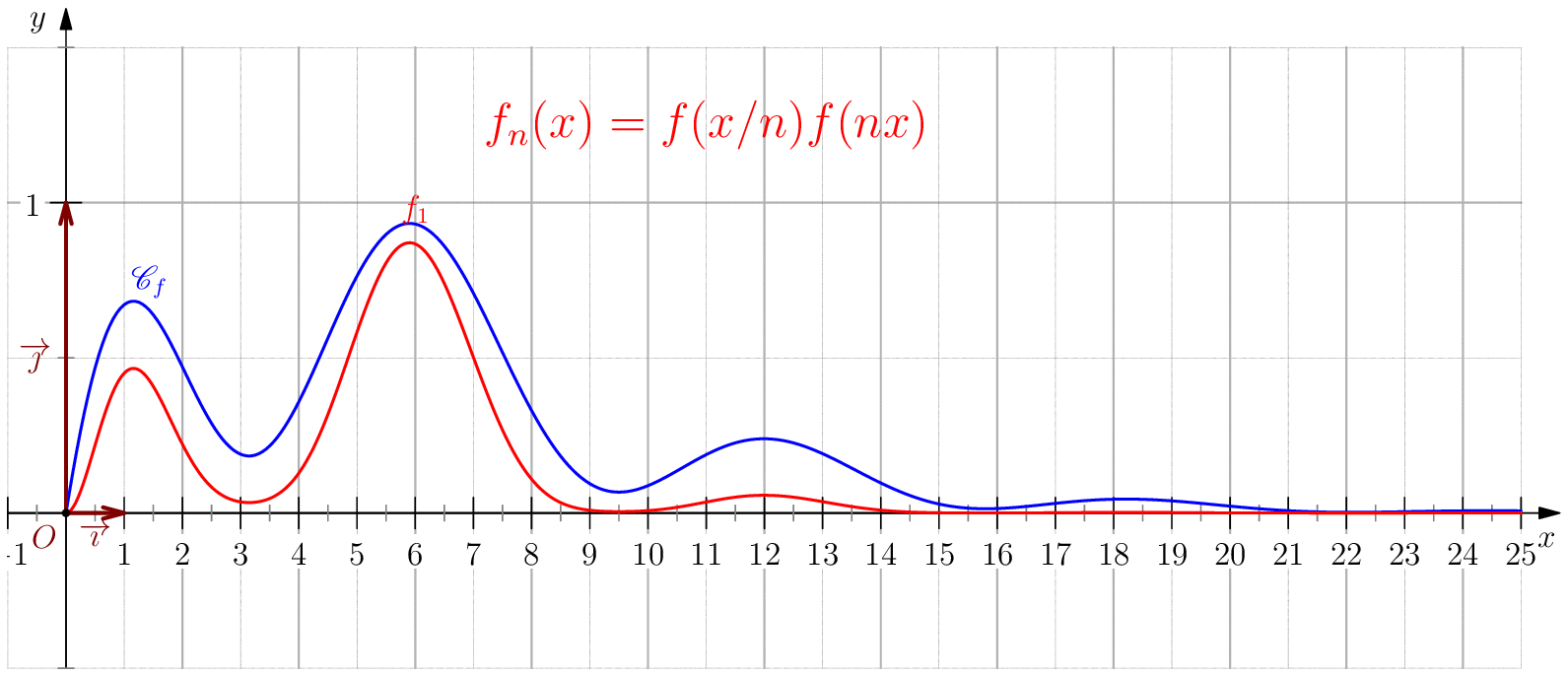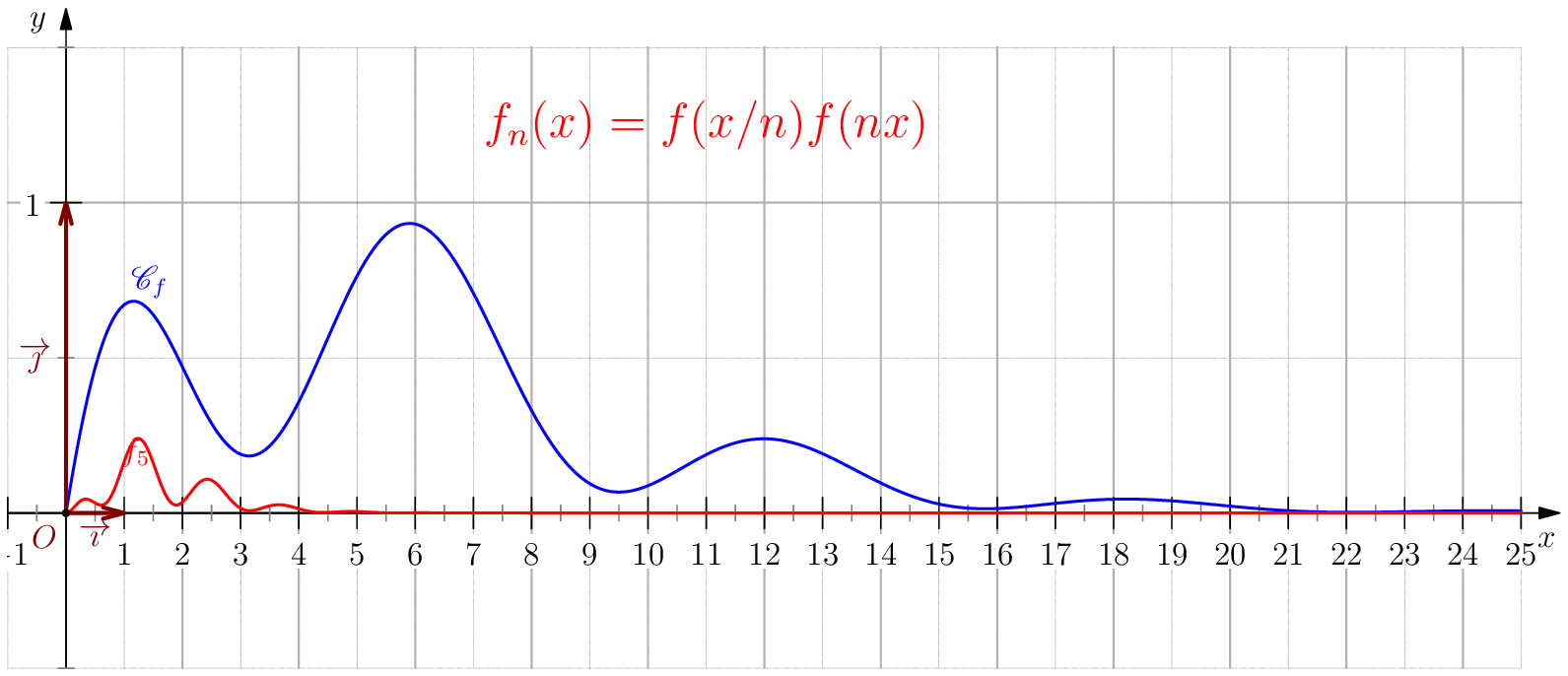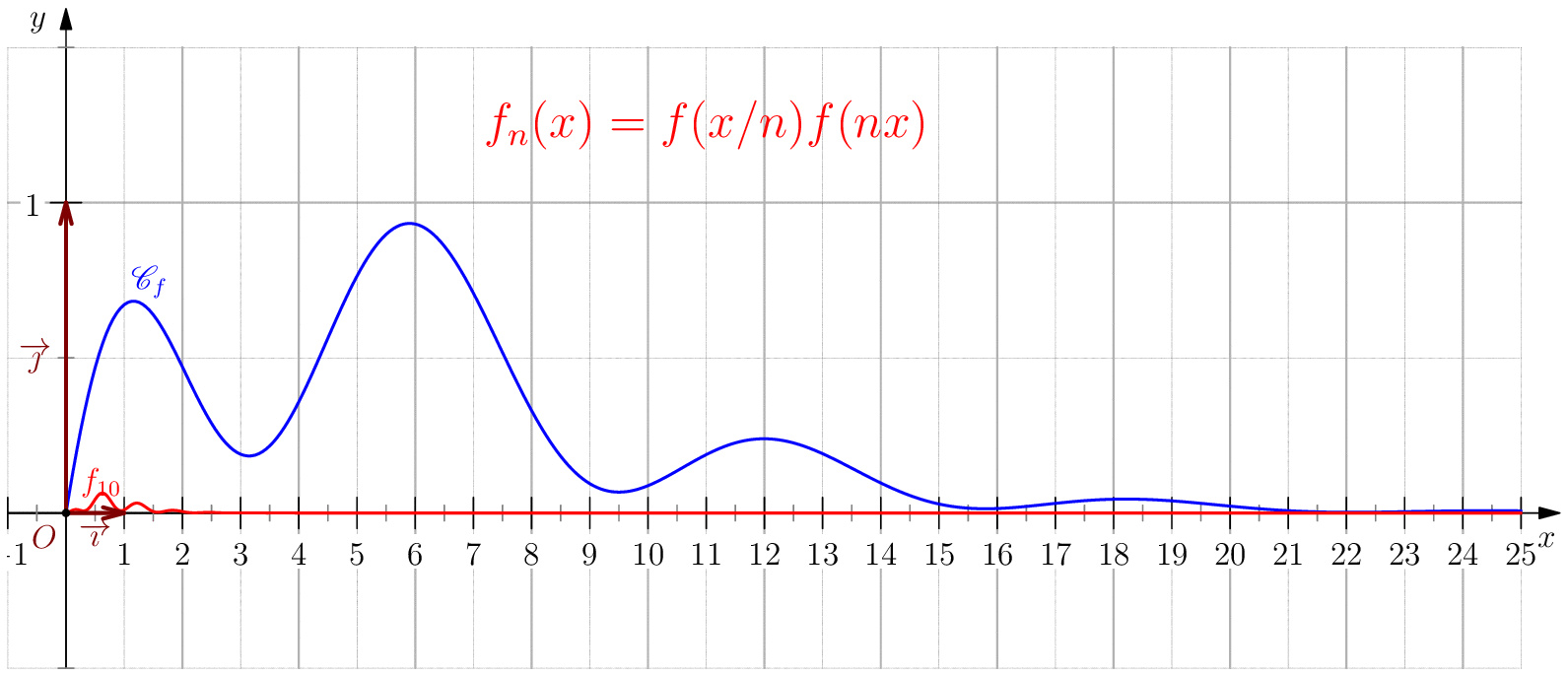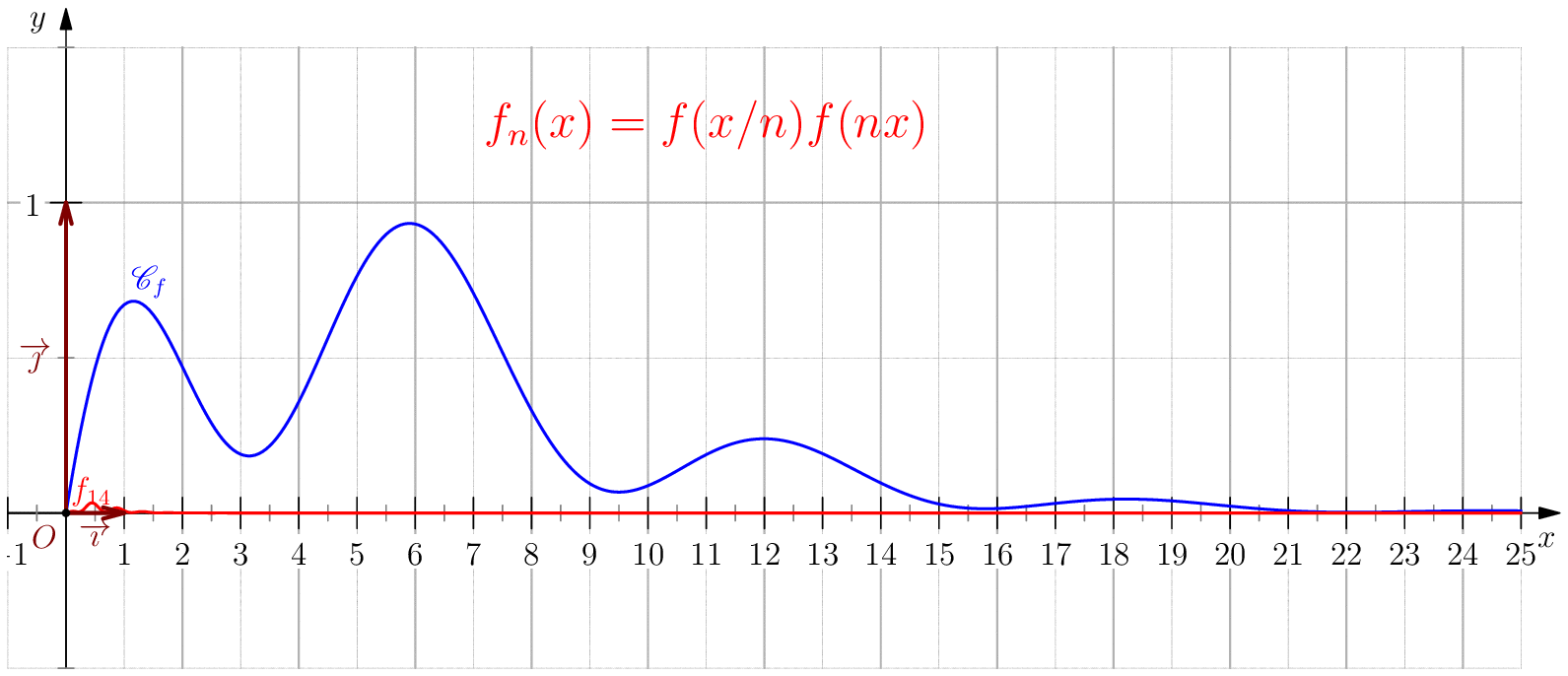
Soit $f$ une application de $\R_+$ dans $\R$ telle que : $f(0)=0 \ , \ \dsp \lim_{x \rightarrow +\infty}{f(x)} = 0 \ $ et $f$ continue sur $\R_+$. Étudier chacune des suites de fonctions définies sur $\R_+$ par : $$\mathbf{a)\,}\,f_n(x) = f(nx);\,\mathbf{b)\,}\,f_n(x)=\dfrac{f(nx)}{n};\,\mathbf{c)\,}\,f_n(x) = f \left(\dfrac{x}{n}\right);\,\mathbf{d)\,}\,~f_n(x) = \dfrac{1}{n}f\left(\dfrac{x}{n}\right);$$ et enfin $\,\mathbf{e)\,}\,~f_n(x)=f(nx)f\left(\dfrac{x}{n}\right).$
Traduisons les données de $f$.
$$\forall \varepsilon>0,\,\exists\eta >0,\forall x\leq \eta,~~\abs{f(x)}\leq \varepsilon,\quad \exists
A>0,~~\forall x\geq A,\,\,\abs{f(x)}\leq \varepsilon.$$
Notons également que dans ce cas $f$ est bornée, de plus il existe $x_1\geq 0$ tel que
$\abs{f(x_1)}=\norme{f}_\infty$.
Le cas $f=0$ est trivial, on suppose alors que $f\neq 0$, i.e. il existe $x_0>0$ tel que
$f(x_0)\neq 0$.
a) Pour tout $x>0$, on a $nx\tendvers{n}{\infty}\infty$, donc $f(nx)\tendvers{n}{\infty}0 $
(car $f$ est continue),
d'autre part comme $f_n(0)=f(0)=0$, on en déduit $\boxed{f_n\overset{C.S}{\longrightarrow} 0}$.
La convergence n'est pas uniforme sur $\R_+$ puisque $\abs{f_n(x_0/n)}=\abs{f(x_0)}>0$.
Pour tout $b>0$, on a $\boxed{f_n\overset{C.U}{\longrightarrow} 0}$ sur $[b,\infty[$ car pour $n\geq
\dfrac{A}{b}$ on a
$nx\geq nb\geq A$ donc $\abs{f_n(x)}=\abs{f(nx)}\leq \varepsilon$.
b) $\boxed{f_n\overset{C.U}{\longrightarrow} 0}$.
c) Pour tout $x\geq 0$, on a $\frac{x}{n}\tendvers{n}{\infty}0$, donc
$f\left(\frac{x}{n}\right)\tendvers{n}{\infty}0 $
(car $f$ est continue), on en déduit $\boxed{f_n\overset{C.S}{\longrightarrow} 0}$.
La convergence n'est pas uniforme sur $\R_+$
puisque $\abs{f_n(nx_0)}=\abs{f(x_0)}>0$.
Pour tout $b>0$, on a $\boxed{f_n\overset{C.U}{\longrightarrow} 0}$ sur $[0,b]$ car pour $n\geq
\dfrac{b}{\eta}$ on a
$\frac{x}{n}\leq \frac{b}{n}\leq \eta$ donc $\abs{f_n(x)}=\abs{f(x/n)}\leq \varepsilon$.
d) $\boxed{f_n\overset{C.U}{\longrightarrow} 0}$.
e) Soit $N\in \N$ tel que $N>\dfrac{A}{\eta}$, alors pour tout $n\geq N$, on a:
$\,--\,$ Pour tout $x\in [\eta,\infty[$, on a $nx\geq n\eta\geq \dfrac{A}{\eta}\eta$, donc
$\abs{f(x/n)f(nx)}\leq \norme{f}_\infty \varepsilon$.
$\,--\,$ Pour $x\in [0,\eta[$, on a $\dfrac{x}{n}\leq x\leq \eta$ donc
$\abs{f(x/n)f(nx)}\leq \norme{f}_\infty \varepsilon$.
Dans tous les cas, on a $\abs{f(x/n)f(nx)}\leq \norme{f}_\infty \varepsilon$ soit
$\boxed{f_n\overset{C.U}{\longrightarrow} 0}$ .
Soit $\big( f_n:\R\mapsto\R\big)_n$ une suite d'application convergeant uniformément vers $f:\R\mapsto\R$.
- Montrer que si $f$ est continue alors $f_n\circ f_n\overset{C.S}{\longrightarrow}f\circ f$.
- Montrer que si $f$ est uniformément continue alors $f_n\circ f_n\overset{C.U}{\longrightarrow}f\circ f$.
Comme $f_n\overset{C.U}{\longrightarrow} f$, alors:
$$\forall \varepsilon>0,\,\exists N_0,\,\forall x\in \R,\,\abs{f_n(x)-f(x)}\leq \varepsilon.$$
1. On suppose que $f$ est continue. Soit $x\in\R$, on a
$$\abs{f_n(f_n(x))-f(f(x))}=\abs{f_n(f_n(x))-f(f_n(x))+f(f_n(x))-f(f(x))}\leq
\abs{f_n(f_n(x))-f(f_n(x))}+\abs{f(f_n(x))-f(f(x))}.$$
Soit $\varepsilon>0$, comme $f$ est continue (en particulier en $f(x)$) alors:
$$\exists \eta>0,~~\forall y\in \R,~~\abs{f(x)-y}\leq \eta\Longrightarrow \varepsilon/2.$$
En utilisant la convergence uniforme de la suite $f_n$, on a:
$$\exists N_1\in \N,~~\forall n\geq N_1,~~\forall z\in \R,~~\abs{f_n(z)-f(z)}\leq \eta.\,\,\exists
N_2\in \N,~~\forall n\geq N_2,~~\forall z\in \R,~~\abs{f_n(z)-f(z)}\leq \varepsilon/2.$$
Pour $n\geq \max (N_1,N_2)$, on a:
$$\abs{f_n(f_n(x))-f(f(x))}\leq
\abs{f_n(f_n(x))-f(f_n(x))}+\abs{f(f_n(x))-f(f(x))}\leq
\varepsilon/2+\varepsilon/2=\varepsilon\Longrightarrow
\boxed{f_n(f_n(x))\tendvers{n}{\infty}f(f(x))}.$$
2. On suppose que $f$ est uniformément continue. Soit $\varepsilon>0$, il existe $\eta>0$
(quitte à remplace $\eta$ par un réel plus petit, on peut supposer que $\eta\leq \varepsilon/2$) tel
que:
$\forall x,y\in \R,~~\abs{x-y}\leq \eta\Longrightarrow \abs{f(x)-f(y)}\leq \varepsilon/2$
La convergence uniforme de la suite $(f_n)$ nous donne: $\exists N\in \N,~~\forall n\geq\N,\,\forall
x\in \R,\,\abs{f_n(x)-f(x)}\leq \eta$. On a donc:
$$\forall n\geq N,~~\forall x\in \R, \abs{f(f_n(x))-f(f(x))}\leq \frac{\varepsilon}{2}\text{ et }
\abs{f_n(f_n(x))-f(f_n(x))}\leq \eta\leq\frac{\varepsilon}{2}.$$
Ce qui donne:
$$\forall n\geq N,\,\forall x\in \R,\,\abs{f_n(f_n(x))-f(f(x))}\leq
\abs{f_n(f_n(x))-f(f_n(x))}+\abs{f(f_n(x))-f(f(x))}\leq \varepsilon\Longrightarrow\boxed{f_n\circ
f_n\overset{C.U}{\longrightarrow} f\circ f}.$$
Soit $f\in \CC^1([0,1],\R)$, pour $n\in \N^*$, on définit $\fonct{f_n}{[0,1]}{\R}{x}{f\left(x+\frac{x(1-x)}{n}\right)}$.
- Montrer que $f_n$ est bien définie.
- Étudier la converge simple (resp. uniforme) de la suite $(f_n)_{n\geq 1}$.
Notons , pour $n\geq 1$ et $x\in [0,1]$, $g_n(x)=x+\dfrac{x(1-x)}{n}$ et $g(x)=x$.
Une étude rapide de $g_n$ montre qu'elle strictement croissante sur l'intervalle $[0,1]$ et
$g_n([0,1])=[g_n(0),g_n(1)]=[0,1]$.
On en déduit que $f_n=f\circ g_n$ est bien définie.
D'autre part $\boxed{g_n\overset{C.U}{\longrightarrow} g}$ sur l'intervalle $[0,1]$
donc en utilisant le résultat de l'exercice \ref{CompCU}, on en déduit
$\boxed{f\circ g_n\overset{C.U}{\longrightarrow} f\circ g=f}$.
-
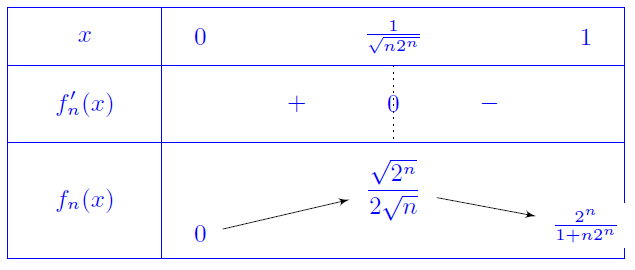
Soit $(f_n)$ la suite de fonctions définies sur $[0,1]$ par : $ f_n(x) = \dfrac{2^n x}{1+n 2^n
x^2}$.
Étudier sa convergence simple sur $[0,1]$. La convergence est-elle uniforme sur $[0,1]$ ? sur
$[\alpha,1]
(0< \alpha< 1)$ ?
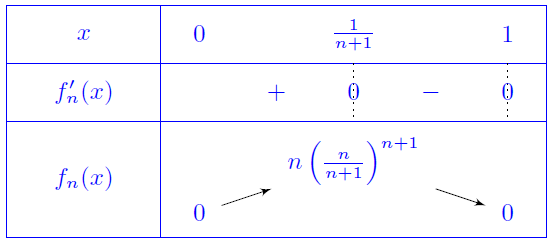
Comparer $\dsp \lim_{n \rightarrow \infty} \dsp \int_0^1{f_n}$ et $ \dsp \int_0^1{ \dsp \lim_{n \rightarrow \infty}{f_n}}$. - Mêmes questions avec : $f_n(x) = n^2 x (1-x)^n \ , \ x\in [0,1]$.
- Déterminer les limites éventuelles, quand $n$ tend vers $+ \infty$, de : $$\mathbf{a)\,}\,\dsp \int_0^1{\dfrac{\ud x}{1+x+...+x^n}},\,\mathbf{b)\,}\,\dsp \int_0^1{\dfrac{n\ee^{-x}+x^2}{n+x} \ud x},\,\mathbf{c)\,}\,\dsp \int_0^1{\dfrac{n(x^3+x)\ee^{-nx}}{n x+1} \ud x}.$$
-
Pour $x\in ]0,1]$, on a $\dfrac{2^n x}{1+n 2^n x^2}\underset{n\infty}{\thicksim}\dfrac{1}{nx}$
donc
$f_n(x)\tendvers{n}{\infty}0$, le résultat reste vraie pour $x=0$.
On en déduit $\boxed{f_n\overset{C.S}{\longrightarrow} 0}$.
Une étude rapide de $f_n$, montre: $$\forall x\in [0,1],\,f_n'(x)=\dfrac{2^n(1-n2^nx^2)}{(1+n2^nx^2)^2}.$$ Donc $f_n'(x)=0$ pour $x_n=\dfrac{1}{\sqrt{n2^n}}$. Comme $f_n(x_n)\tendvers{n}{\infty}\infty$, on en déduit que $(f_n)$ ne converge pas uniformément vers $0$.
Soit $n\geq 1$, on a: $$\int_0^1f_n(x)\ud x=\dfrac{1}{2n}\left[\ln\left(1+n2^nx^2\right)\right]_0^1=\dfrac{\ln(1+n2^n)}{2n}\tendvers{n}{\infty}\dfrac{\ln(2)}{2}.$$ D'autre part, $\dsp \int_0^1{ \dsp \lim_{n \rightarrow \infty}{f_n}}=\int_0^10=0$. On en déduit $\boxed{\dsp \lim_{n \rightarrow \infty} \dsp \int_0^1{f_n} \neq \dsp \int_0^1{ \dsp \lim_{n \rightarrow \infty}{f_n}}}$. -
Pour $x\in ]0,1[$, on a $f_n(x)\tendvers{n}{\infty}0$, le résultat reste vraie pour $x=0$ et
$x=1$.
On en déduit $\boxed{f_n\overset{C.S}{\longrightarrow} 0}$.
Une étude de $f_n$, montre:
$$\forall x\in [0,1],\,f_n'(x)=n^2(1-x)^{n-1}\left(1-(1+n)x\right).$$
Donc $f_n'(x)=0$ pour $x_n=\dfrac{1}{n+1}$.
Comme $f_n(x_n)\tendvers{n}{\infty}\infty$, on en déduit que $(f_n)$ ne converge pas
uniformément
vers $0$.
Soit $n\geq 1$, on a: $$\int_0^1f_n(x)\ud x\underset{u=1-x}{=}n^2\int_0^1(1-u)u^n\ud u=n^2\left[\frac{u^{n+1}}{n+1}-\frac{u^{n+2}}{n+2}\right]_0^1=\dfrac{n^2}{(n+1)(n+2)}\tendvers{n}{\infty}1.$$ D'autre part, $\dsp \int_0^1{ \dsp \lim_{n \rightarrow \infty}{f_n}}=\int_0^10=0$. On en déduit $\boxed{\dsp \lim_{n \rightarrow \infty} \dsp \int_0^1{f_n} \neq \dsp \int_0^1{ \dsp \lim_{n \rightarrow \infty}{f_n}}}$. -
- On définit pour $n\in \N^*$, $\fonct{u_n}{[0,1]}{\R}{x}{\frac{1}{1+\cdots+x^n}}$.
On a $u_n\overset{CU}{\tendvers{n}{\infty}}u$ avec $u(x)=1-x$, en effet, pour $x\in [0,1[$ on a $u_n(x)=\dfrac{1-x}{1-x^{n+1}}\tendvers{n}{\infty}1-x$ puis $u_n(1)=\dfrac{1}{n+1}\tendvers{n}{\infty}0=u(1)$ ce qui montre la convergence simple de la suite $(u_n)$ vers $u$.
Ensuite, en étudiant la fonction $g_n=u_n-u$ sur $[0,1[$, on a $$g_n'(x)=\left(\dfrac{x^{n+1}}{1+x+\cdots+x^n}\right)'=\dfrac{(n+1)x^n\dsum_{k=0}^nx^k-x^{n+1}\dsum_{k=0}^nkx^{k-1}}{\left(\dsum_{k=0}^nx^k\right)^2}=\dfrac{x^n}{\left(\dsum_{k=0}^nx^k\right)^2}\left(\dsum_{k=0}^n(n+1-k)x^k\right)\geq 0,$$ donc $g_n$ est croissante sur $[0,1[$, ce qui donne $$\forall x\in [0,1],~~g_n(x)\leq \limiteX{t}{1}g_n(t)=\dfrac{1}{n+1}\Longrightarrow\norme{u_n-u}_\infty\leq \frac{1}{n+1}\tendvers{n}{\infty}0.$$ On en déduit, $$\boxed{\limiteX{n}{\infty}\int_0^1u_n(x)\ud x=\int_0^1u(x)\ud x=\dfrac{1}{2}}.$$ - On pose, pour $n\geq 1$, $f_n(x)=\dfrac{n\ee^{-x}+x^2}{n+x}$, on a $$\forall x\in [0,1],~~\abs{f_n(x)-\ee^{-x}}=\abs{\dfrac{x^2-x\ee^{-x}}{x+n}}\leq \dfrac{2}{n}\tendvers{n}{\infty}0\Longrightarrow f_n\overset{CU}{\longrightarrow}f,~~\text{ avec } f(x)=\ee^{-x}.$$ On en déduit, $$\boxed{\limiteX{n}{\infty}\int_0^1f_n(x)\ud x=\int_0^1\ee^{-x}\ud x=1-\ee^{-1}}.$$
- On définit pour $n\in \N^*$, $\fonct{u_n}{[0,1]}{\R}{x}{\frac{n(x^3+x)\ee^{-nx}}{nx+1}}$.
On a $u_n\overset{CS}{\tendvers{n}{\infty}}0$, cependant cette convergence n'est pas
uniforme puisque
$u_n(1/n)=\dfrac{\ee^{-1}}{2}(1+\frac{1}{n^2})>0$.
Soit $a\in ]0,1[$, la suite $(u_n)$ converge uniformément vers $0$ sur $[a,1]$, car, $$\forall x\in [a,1],~~ 0< u_n(x)\leq \dfrac{2\ee^{-na}}{a+1/n}\leq \dfrac{2\ee^{-na}}{a} \tendvers{n}{\infty}0$$ Ce qui donne $\dsp\limiteX{n}{\infty}\int_a^1u_n(x)\ud x=0$. D'autre part, pour tout $n\in \N$, $$\int_0^au_n(x)\ud x\leq \int_0^n\dfrac{x^3+x}{x+\frac{1}{n}}\ud x\leq \int_0^1(x^2+1)\ud x=a+a^3/3.$$ On a montré: $$\forall n\in \N,~~0\leq \int_0^1u_n(x)\ud x\leq a+\frac{a^3}{3}+\int_a^1u_n(x)\ud x\Longrightarrow 0\leq \limiteX{n}{\infty}\int_0^1u_n(x)\ud x\leq a+\frac{a^3}{3}+\limiteX{n}{\infty}\int_a^1u_n(x)\ud x= a+\frac{a^3}{3}.$$ Cette dernière relation est vrai pour tout $a\in ]0,1[$, en faisant $a$ tendre vers $0$ on trouve : $\boxed{\limiteX{n}{\infty}\int_0^1u_n(x)\ud x=0}$.
- On définit pour $n\in \N^*$, $\fonct{u_n}{[0,1]}{\R}{x}{\frac{1}{1+\cdots+x^n}}$.
En étudiant $ \dsp \lim_{n \rightarrow +\infty}{ \dsp \int_0^1{x^n(1-x)^n \ud x}}$, démontrer que : $ \dsp \lim_{n\rightarrow +\infty}{\dsp \sum_{p=0}^n{ \dfrac{(-1)^p \binom{n}{p}}{2 n -p+1}}} = 0$.
On pose $f_n(x)=x^n(1-x)^n$, la suite $f_n$ converge uniformément vers $0$ sur $[0,1]$
(car $\norme{f_n}_\infty=\frac{1}{4^n}\tendvers{n}{\infty}\,0$).
On en déduit:
$\boxed{\dsp\limiteX{n}{\infty}\int_0^1f_n(x)\ud x=\int_0^1\limiteX{n}{\infty}f_n(x)\ud x=0}$.
D'autre part,
$$\int_0^1f_n(x)\ud x=\int_0^1x^n\left(\dsum_{p=0}^n\binom{n}{n-p}(-1)^{n-p}x^{n-p}\right)\ud
x=(-1)^n\dsum_{p=0}^n\binom{n}{p}(-1)^p\int_0^1x^{2n-p}=(-1)^n\sum_{p=0}^n \dfrac{(-1)^p
\binom{n}{p}}{2 n -p+1}.$$
On considère la suite d'applications de $[-1,1]$ dans $\R$ définie par: $$\forall x\in [-1,1],~~~~f_0(x)=2x,\quad\quad\forall n\in \N,\,\,\forall x\in [-1,1],\,f_{n+1}(x)=\sqrt{2+f_n(x)}.$$
- Étudier la convergence simple et uniforme de la suite $(f_n)_n$ sur $[-1,1]$.
- Pour $n\in \N$, on pose $I_n=\dsp\int_{-1}^1f_n(t)\ud\,t$. Étudier la convergence de la suite $(I_n)_n$.
- Pour $n\in \N$, on pose $J_n=\dsp\int_{-1}^1\frac{\ud \,t}{f_n(t)}$. Étudier la convergence de la suite $(J_n)_n$.
On montre par récurrence sur $n\geq 1$ la relation suivante:
$\mathcal{H}_n:\quad\forall x\in [-1,1],\, f_n(x)\in [0,2]$.
Puis, pour tout $n\geq 2$ et $x\in [-1,1]$, on a :
$$\abs{f_{n+1}(x)-2}=\abs{\sqrt{2+f_n(x)}-\sqrt{2+2}}=\abs{\dfrac{f_n(x)-2}{\sqrt{2+f_n(x)}+2}}\leq
\dfrac{\abs{f_n(x)-2}}{2}\Longrightarrow \norme{f_{n+1}-2}_\infty\leq
\dfrac{\norme{f_n-2}_\infty}{2}.$$
Puis par récurrence sur $n\in \N$, $\boxed{\norme{f_n-2}_\infty\leq \dfrac{4}{2^n}}$.
On en déduit que $f_n\overset{C.U}{\tendversN}\,2$ sur l'intervalle $[-1,1]$. Ce qui donne
$$\limiteX{n}{\infty}\int_{-1}^1f_n(x)\ud x=\int_{-1}^12\ud x=4\Longrightarrow \boxed{
I_n\tendversN\,4}.$$
Pour l'intégrale $J_n$, notons d'abord que $J_n$ n'est définie que pour $n\geq 1$.
Soit $n\geq 2$, on a
$$\forall x\in [-1,1],\quad
\abs{\dfrac{1}{f_{n}(x)}-\dfrac{1}{2}}=\abs{\dfrac{2-f_{n}(x)}{2f_n(x)}}\leq
\dfrac{\norme{f_n-2}_\infty}{2}\Longrightarrow
\boxed{\dfrac{1}{f_n}\overset{C.U}{\tendversN}\,\dfrac{1}{2}}.$$
On en déduit $\boxed{ J_n\tendversN\,1}$.
Soit $I$ un intervalle de $\R$ et $(f_n)_n$ une suite de fonctions définies sur $I$ dans $\R$.
On suppose que $f_n\overset{CU}{\tendversN}f$.
Que peut-on dire de la suite $\left(\dfrac{f_n}{1+f_n^2}\right)_n$?
Notons, pour $x\in \R$, $g(x)=\dfrac{x}{1+x^2}$. Alors $g$ est continue sur $\R$, de plus, $$\forall x\in \R,\,g'(x)=\dfrac{1-x^2}{(1+x^2)^2}\Longrightarrow \forall x\in \R,\,\abs{g'(x)}\leq 1\Longrightarrow \quad \norme{g'}_\infty\leq 1.$$ Soit $x\in \R$, la suite $(f_n(x))$ converge vers $f(x)$, comme $g$ est continue en $f(x)$ alors $g(f_n(x))\tendversN\,g(f(x))$. On en déduit, $$\dfrac{f_n}{1+f_n^2}=g(f_n)\overset{CS}{\tendvers{n}{\infty}}g(f)=\dfrac{f}{1+f^2}.$$ D'autre part, $$\forall x\in \R,\quad \abs{g(f_n(x))-g(f(x))}\leq \norme{g'}_\infty \abs{f_n(x)-f(x)} \Longrightarrow \norme{g(f_n)-g(f)}_\infty \leq \norme{f_n-f}_\infty \tendversN\,0.$$ On en déduit que $\dfrac{f_n}{1+f_n^2}\overset{CU}{\tendvers{n}{\infty}}\dfrac{f}{1+f^2}$.
Pour $n\in \N^*$, on définit $f_n:\,\R\longmapsto \R$ par $f(x)=\left\{\begin{array}{lcl} \dfrac{\sin(nx)^2}{nx}&\text{si }& x\neq 0\\ 0&\text{ si }& x=0. \end{array}\right.$.
- Montrer que $f_n$ est bornée sur $\R$.
- Montrer que la suite $(f_n)_n$ converge simplement sur $\R$. La convergence est-elle uniforme?
-
Montrons que $f_n$ est continue sur $\R$. Il est clair que $f_n$ est continue sur $\R^*$, il
faut juste voir
la continuité en $0$.
Au voisinage de $0$, on a $f_n(x)\underset{x\to 0}{\thicksim}nx$, donc $\limiteX{x}{0}f_n(x)=0=f_n(0)$, ce qui prouve la continuité de $f_n$ en $0$ donc sur $\R$.- Comme $f_n\in \CC([-1,1])$ alors $f_n$ est majoré sur cet intervalle par une constante $C_1>0$.
- Pour $x\in \R$ tel que $\abs{x}>1$ on a $\abs{f_n(x)}\leq \dfrac{1}{n\abs{x}}\leq 1$.
-
Pour $x\in \R^*$, on a $\abs{f_n(x)}\leq \dfrac{1}{n\abs{x}}\tendversN 0$, d'autre part,
$f_n(0)=0$. On en déduit que $f_n\overset{C.S}{\tendversN}0$.
D'autre part, pour $x=\dfrac{\pi}{2n}$, on a $f_n(x)=\dfrac{\sin^2\left(\frac{\pi}{2}\right)}{\frac{\pi}{2}}=\dfrac{2}{\pi}$ ne tend pas vers $0$, donc la convergence n'est pas uniforme sur $\R$.
Soit $a>0$, pour tout $x\in \R\setminus]-a,a[$, on a $\abs{f_n(x)}\leq \dfrac{1}{na}$ donc $\norme{f_n}_\infty^{\R\setminus]-a,a[}\leq \dfrac{1}{na}\tendversN 0$, on en déduit que la suite $(f_n)_n$ converge uniformément vers $0$ sur tout intervalle de type $\R\setminus ]-a,a[$ avec $a>0$.
Soit $I$ un intervalle de $\R$ et $(f_n)_n$ (resp. $(g_n)_n$) une suite de fonctions définies sur $I$ dans $\R$. On suppose que $f_n\overset{CU}{\tendversN}f$ (resp. $g_n\overset{CU}{\tendversN}g$).
- Montrer que $f_n+g_n\overset{CU}{\tendversN}f+g$. A-t-on $f_ng_n\overset{CU}{\tendversN}fg$?
- On suppose que $f,\,g$ sont bornées sur $I$. Montrer que $f_ng_n\overset{CU}{\tendversN}fg$.
-
Pour tout $n\in \N$ (assez grand pour que $f-f_n$ et $g-g_n$ soient bornées) et $x\in I$, on a
$$\abs{(f+g)(x)-(f_n+g_n)(x)}\leq \abs{f(x)-f_n(x)}+\abs{g(x)-g_n(x)}\leq \norme{f-f_n}_\infty+
\norme{g-g_n}_\infty.$$
Donc $(f+g)-(f_n+g_n)$ est borne (au moins à partir d'un certain rang) et on a
$$\norme{(f+g)-(f_n+g_n)}_\infty\leq \norme{f-f_n}_\infty+ \norme{g-g_n}_\infty\Longrightarrow
\norme{(f+g)-(f_n+g_n)}_\infty\tendversN\,0.$$
Ce qui prouve que $\boxed{f_n+g_n\overset{C.U}{\tendversN}f+g}$.
Posons maintenant, pour $n\in \N$, $f_n(x)=g_n(x)=x+\dfrac{1}{n+1}$ et $f(x)=x$. On a $f_n\overset{C.U}{\tendversN} f$ sur $\R$ puisque $\norme{f-f_n}=\dfrac{1}{n+1}\tendversN\,0$.
Par contre, $(f^2-f_n^2)(x)=\dfrac{2x}{n+1}+\dfrac{1}{n+1}$, en particulier, $(f^2-f_n^2)(\frac{1}{n+1})\geq 2$, donc il n'y a pas de convergence uniforme. - Supposons maintenant que $f$ et $g$ sont bornées sur $I$. Alors pour $n\geq n_0$ les fonctions $f_n$ et $g_n$ sont bornées. Alors, pour tout $n\geq n_0$ et pour tout $x\in I$, $$\begin{array}{lcl} \abs{(fg)(x)-(f_ng_n)(x)}&=&\abs{f(x)g(x)-f(x)g_n(x)+f(x)g_n(x)-f_n(x)g_n(x)}\\ &\leq & \abs{f(x)}\abs{g(x)-g_n(x)}+\abs{g_n(x)}\abs{f(x)-f_n(x)}\\ &\leq& \norme{f}_\infty \norme{g-g_n}_\infty+\norme{g_n}_\infty\norme{f-f_n}_\infty. \end{array}$$ Ce qui prouve que $\boxed{f_ng_n\overset{C.U}{\tendversN}fg}$
Pour $n\in \N$, on pose $\fonct{f_n}{[0,1]}{\R}{x}{3^n\left(x^{2^n}-x^{2^{n+1}}\right)}$.
- Étudier la convergence de la suite $(f_n)$.
- Comparer $\limiteX{n}{\infty}\dsp\int_0^1f_n(x)\ud x$ et $\dsp\int_0^1\limiteX{n}{\infty}f_n(x)\ud x$
-
On a,
- Pour $x\in \{0,1\}$, et pour tout $n\in \N$, $f_n(x)=0$. Donc $f_n(x)\tendversN\,0$
- Pour $x\in ]0,1[$, on a $3^nx^{2^n}\tendversN 0$ donc $f_n(x)\tendversN 0$
Pour $x_n=\exp\left(\frac{\ln(1/2)}{2^n}\right)$, on a $f_n(x_n)=\dfrac{3^n}{4}>\dfrac{1}{4}$ donc la convergence n'est pas uniforme. - Soit $n\in \N$, on a $$\int_0^1f_n(x)=3^n\left(\dfrac{1}{2^n+1}-\dfrac{1}{2^{n+1}+1}\right)=3^n\dfrac{2^n}{(2^n+1)(2^{n+1}+1)}\underset{n\to \infty}{\thicksim}\dfrac{6^n}{2\,4^n}\tendversN\infty.$$ D'autre part, on a$\dsp\int_0^1\limiteX{n}{\infty}f_n=0$. Donc $\boxed{\dsp\limiteX{n}{\infty}\int_0^1f_n(x)\ud x\neq \int_0^1\limiteX{n}{\infty}f_n(x)\ud x}$.
Soit $(f_n)_{n\in\mathbb N}$ la suite de fonctions définie par : $\forall x\in I=[-1,1],\ f_n(x)=\sin(nx\ee^{-x^2n})$.
- Montrer que $(f_n)$ converge simplement sur $I$ vers une fonction $F$ que l'on définira.
- Montrer que $(f_n)$ converge uniformément sur $[a,1]$, où $a\in \left]0,1\right]$.
- $(f_n)$ converge-t-elle uniformément sur $I$ ?
$f_n$ CS vers 0.
Pas de CU...il suffit de calculer $f_n(1/\sqrt{n}$.
Soit $(f_n)$ une suite de fonctions monotones convergeant simplement vers $f$ sur un intervalle $I$ de $\R$. Montrer que $f$ est monotone.
Supposons que les fonctions $f_n$ sont croissante. Soient $x_1< x_2\in I$. Alors pour tout $n\in \N$, on a $f_n(x_1)\leq f_n(x_2)$ ce qui donne: $$f(x_1)=\limiteX{n}{\infty}f_n(x_1)\leq \limiteX{n}{\infty}f_n(x_2)=f(x_2)\Longrightarrow f \text{ est croissante}.$$
Soit $(P_n)$ une suite de fonctions polynomiales de degré inférieur ou égale à $p\in \N$. On suppose que $(P_n)$ converge simplement vers $f$ sur $\R$.
- Montrer que $f$ est une fonction polynomiale de degré inférieur ou égale à $p$.
- Montrer que la convergence est uniforme sur tout segment de $\R$. Que dire si cette convergence est uniforme sur $\R$?
- Soit $a_0,\cdots,a_p$, $p+1$ points de $\R$ deux à deux distincts. On considère les polynômes de Lagrange associes à ces points, i.e. $$\forall j\in \inter{0,p},\quad L_j(x)=\prod_{\substack{0\leq k\leq p \\k\neq j}}\dfrac{x-a_k}{a_j-a_k}.$$ D'après le cours, pour tout $P\in\R_p[x]$, on a $P=\dsum_{k=0}^pP(a_k)L_k$, en particulier, $$\forall n\in \N,\,\forall x\in \R,\, P_n=\dsum_{k=0}^pP_n(a_k)L_k(x) \Longrightarrow \forall x\in \R,\, \limiteX{n}{\infty} P_n(x)= \dsum_{k=0}^p\limiteX{n}{\infty}(P_n(a_k))L_k(x).$$
-
Soient $a< b$ deux réels, comme les fonctions $(L_j)_{j\in \inter{0,p}}$ sont continues sur
$[a,b]$, alors elles y sont bornées.
Notons alors $M=\dsp\sup_{j\in \inter{0,p}}(\norme{L_j}_\infty^{[a,b]})$. Alors, pour tout
$n\in \N$ et $x\in [a,b]$, on a
$$ \abs{f(x)-P_n(x)}\leq \dsum_{j=0}^p\abs{f(a_j)-P_n(a_j)}\abs{L_j(x)}\leq
M\dsum_{j=0}^p\abs{f(a_j)-P_n(a_j)} \Longrightarrow \norme{f-P_n}_\infty^{[a,b]}\leq M
\dsum_{j=0}^p\abs{f(a_j)-P_n(a_j)}\tendversN\,0.$$
Ce qui prouve la convergence uniforme sur $[a,b]$.
Supposons maintenant que $P_n$ converge uniformément vers $f$ sur $\R$, ceci implique que à partir d'un certain range, la fonction $f-P_n$ est bornée sur $\R$, or $f-P_n$ est une fonction polynomial, ceci impose alors que $f-P_n$ est une constante.
On en déduit alors que si $P_n$ converge uniformément vers $f$ sur $\R$, alors il existe $N\geq 0$ et une suite réel $(\alpha_n)$ qui tend vers $0$ telles que $$\forall n\geq N,\quad P_n=f+\alpha_n.$$
Series de fonctions
Étudier (CS, CU, CN) les séries d'applications $\dsp\sum f_n$ suivantes:
- $f_n:\R\mapsto\R,~~f_n(x)=x\ee^{-nx^2}$
- $f_n:[0,1]\mapsto\R,~~n^2(x^{2n}-x^{2n+1})$
- $f_n:\R\mapsto\R,~~f_n(x)=\dfrac{(-1)^n}{n^x}$
- $f_n:\R\mapsto\R,~~f_n(x)=\dfrac{1}{n^x}$
- $f_n:\R_+\mapsto\R,~~f_n(x)=(-1)^n\ln\left(1+\dfrac{x}{n(1+x)}\right)$
-
$f_n:\R\mapsto\R,~~f_n(x)=x\ee^{-nx^2}$.
Soit $x\in \R^*$, on a $n^2f_n(x)=n^2x\ee^{-nx^2}\tendvers{n}{\infty}0$ donc $\dsum_{n\geq 0}f_n(x)$ converge (Rappel : $n^2f_n(x)=\dfrac{f_n(x)}{\frac{1}{n^2}}$ ). Donc $\dsum_n f_n$ converge simplement sur $\R$.
Une étude rapide de $f_n$ (fonction impaire), montre: $$\forall x\in [0,1],\,f_n'(x)=(1-2nx^2)\ee^{-nx^2}.$$ Donc $\norme{f_n}_{\infty}=\dfrac{1}{\sqrt{2\ee n}}$, or $\dsum_{n\geq 1}\dfrac{1}{\sqrt{2\ee n}}$ diverge.
On en déduit que $\dsum f_n$ ne converge pas normalement sur $\R$.
Il faut regarder la convergence uniforme sur $\R$, soit $x\in \R^*$, on a: $$R_n(x)=\dsum_{k=n+1}^\infty x\ee^{-kx^2}=\dfrac{x\ee^{-(n+1)x^2}}{1-\ee^{-x^2}}\Longrightarrow R_n(1/\sqrt{n+1})=\dfrac{1}{\ee\sqrt{n+1}(1-\ee^{\frac{-1}{n+1}})}\underset{n\infty}{\thicksim}\dfrac{\sqrt{n+1}}{\ee}$$ Donc $(R_n)$ ne converge pas uniformément vers $0$ sur $\R$.
En résumé- $\dsum_n f_n$ converge simplement sur $\R$.
- Pour tout $a>0$, $\dsum_n f_n$ converge normalement sur $\R\setminus ]-a,a[$.
- $\dsum_n f_n$ ne converge pas uniformément sur $\R$.
- $f_n:[0,1]\mapsto\R,~~f_n(x)=n^2(x^{2n}-x^{2n+1})$.
Soit $x\in ]0,1[$, en utilisant la règle d'Alembert $\dsum_{n\geq 0}f_n(x)$ converge, également $\dsum_nf_n(0),\,\dsum_nf_n(1)$ converge. Donc $\dsum_n f_n$ converge simplement sur $[0,1]$. Une étude rapide de $f_n$, montre: $$\forall x\in [0,1],\,f_n'(x)=n^2x^{2n-1}(2n-(2n+1)x).$$ Donc $\norme{f_n}_{\infty}=\dfrac{n^2}{2n+1}\left(1+\frac{1}{2n}\right)^{-2n} \underset{n\infty}{\thicksim}\dfrac{n^2\ee^{-1}}{2n}\tendvers{n}{\infty}\infty$. Or $\dsum_{n\geq 1}\dfrac{1}{\sqrt{2\ee n}}$ diverge.
On en déduit que $\dsum f_n$ ne converge pas normalement sur $[0,1]$.
Comme $f_n(x_n)\tendvers{n}{\infty}\infty$, on en déduit que $(f_n)$ ne converge pas uniformément vers $0$.
Comme $\norme{f_n}_\infty\tendvers{n}{\infty}\infty$, on en déduit que $\dsum_n f_n$ ne converge pas uniformément sur $[0,1]$.
En résumé- $\dsum_n f_n$ converge simplement sur $[0,1]$.
- Pour tout $a\in ]0,1[$, $\dsum_n f_n$ converge normalement sur $[0,a]$.
- $\dsum_n f_n$ ne converge pas uniformément sur $[0,1]$.
- $f_n:\R\mapsto\R,~~f_n(x)=\dfrac{(-1)^n}{n^x}$.
Pour $x\leq 0$, $\dfrac{(-1)^n}{n^x}\xcancel{\xrightarrow[n\rightarrow \infty]{}\,0 }$ donc $\dsum_n f_n(x)$ diverge. Pour $x>0$, la suite $(\dfrac{(-1)^n}{n^x})_n$ est strictement décroissante et tend vers $0$ donc d'après la CSSA, on a $\dsum_nf_n(x)$ converge. On en déduit que $\dsum_nf_n$ converge simplement sur $\R_+^*$.
Pour $n\geq 1$, on a $\norme{f}_\infty^{\R_+}=1$ donc $\dsum_n f_n$ ne converge pas normalement sur $\R_+^*$, en revanche pour $b>1$ on $\norme{f}_\infty^{[b,\infty[}=\dfrac{1}{n^b}$ donc $\dsum_nf_n$ converge normalement sur $[b,\infty[$.
$\dsum_nf_n$ ne converge pas uniformément sur $\R_+^*$ puisque $\norme{f}_\infty^{\R_+}=1$. Soit $a>0$,d'après le cours sur les séries alternées, on a : $$\forall n\geq 1,\,\forall x\geq a,~~\abs{R_n(x)}=\abs{\dsum_{k\geq n+1}\dfrac{(-1)^k}{k^x}}\leq \dfrac{1}{(n+1)^x}\leq \dfrac{1}{(n+1)^a}\Longrightarrow \norme{R_n}_\infty^{[a,\infty[} \tendvers{n}{\infty}0.$$ Donc $\dsum_nf_n$ converge uniformément sur $[a,\infty[$.
En résumé- $\dsum_n f_n$ converge simplement sur $]0,\infty[$.
- Pour tout $b>1$, $\dsum_n f_n$ converge normalement sur $[b,\infty[$.
- Pour tout $a>0$, $\dsum_n f_n$ converge uniformément sur $[a,\infty[$.
- $f_n:\R\mapsto\R,~~f_n(x)=\dfrac{1}{n^x}$.
Répons:- $\dsum_n f_n$ converge simplement sur $]1,\infty[$.
- $\dsum_n f_n$ ne converge pas uniformément sur $]1,\infty[$.
- Pour tout $b>1$, $\dsum_n f_n$ converge normalement sur $[b,\infty[$.
- $f_n:\R_+\mapsto\R,~~f_n(x)=(-1)^n\ln\left(1+\dfrac{x}{n(1+x)}\right)$.
Soit $x>0$, la suite $\left(\ln\left(1+\dfrac{x}{n(1+x)}\right)\right)_n$ est décroissante de plus $\ln\left(1+\dfrac{x}{n(1+x)}\right)\tendvers{n}{\infty}\,0$ donc d'après le CSSA $\dsum_n f_n(x)$ converge, le résultat est évident pour $x=0$. Donc $\dsum_n f_n $ converge simplement sur $\R_+$.
On n' a pas une convergence normale sur $\R_+$ puisque $\norme{f_n}_\infty=\ln\left(1+\frac{1}{n}\right)\underset{n\infty}{\thicksim}\dfrac{1}{n}$ et $\dsum_{n\geq 1}\dfrac{1}{n}$ diverge.
Soit $x\geq 0$, on a $$\forall n\in \N,~~\forall x\geq 0,~~\abs{R_n(x)}\leq \ln\left(1+\dfrac{x}{(n+1)(x+1)}\right)\leq \ln\left(1+\dfrac{1}{(n+1)}\right)\Longrightarrow \norme{R_n}_\infty^{[0,\infty[}\tendvers{n}{\infty}0.$$ Donc $\dsum_n f_n$ converge uniformément sur $\R_+$. - $n\geq 1,~~f_n:\R_+\mapsto\R,~~f_n(x)=\left\{\begin{array}{ll} \dfrac{1}{n}&\text{ si } x\in ]n,n+1[\\ &\\ 0&\text{ sinon} \end{array} \right. $
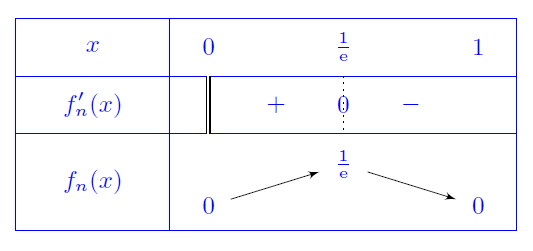
Montrer que la série de fonction $\dsp \sum_{n=0}^{\infty}{ \dfrac{(-x \ln x)^n}{n!}}$
converge normalement sur $[0,1]$.
En déduire : $\dsp \int_0^1{x^{-x} \ud x} = \dsp
\sum_{n=1}^{+\infty}{n^{-n}}$.
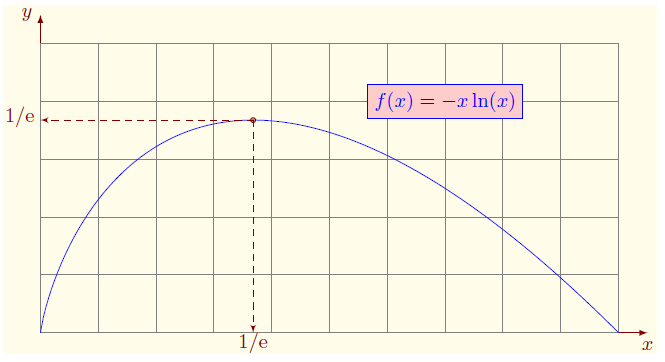
Soit $f$ la fonction définie sur $[0,1]$ par $f(x)=\left\{\begin{array}{lcl}
-x\ln(x)& \text{ si }& x>0\\
0&\text{ si }& x=0
\end{array}\right.
$, $f$ est continue sur $[0,1]$.
L'étude de $f$ montre que $f$ est bornée sur $[0,1]$ et $\norme{f}_\infty=\dfrac{1}{\ee}$.
Posons pour $n\in \N$ et $x\in [0,1]$, $f_n(x)=\dfrac{(-x\ln(x))^n}{n!}=\dfrac{f(x)^n}{n!}$.
L'étude précédente montre $f_n$ est bornée et $\norme{f_n}_\infty=\dfrac{(1/\ee)^n}{n!}$, comme la
série $\dsum_{n\geq 0}\dfrac{(1/\ee)^n}{n!}$ converge (et sa somme est $\ee^{1/\ee}$),
on en déduit que $\dsum_{n\geq 0}f_n$ converge normalement sur $[0,1]$.
Pour $x\in [0,1]$, on écrit $x^{-x}=\ee^{-x\ln(x)}=\dsum_{n\geq 0}\dfrac{(-x\ln(x))^n}{n!}$,
$$\int_0^1x^{-x}\ud x=\int_0^1\left(\dsum_{n\geq 0}\dfrac{(-x\ln(x))^n}{n!}\right)\ud x=
\dsum_{n\geq 0}\dfrac{1}{n!}\int_0^1(-x\ln(x))^n\ud x.$$
En faisant une intégration par partie, on trouve
$$\begin{array}{lcl}
\dsp \int_0^1(-x\ln(x))^n\ud
x&=& \dsp \left[\dfrac{-(-x)^{n+1}}{n+1}(\ln(x))^n\right]_0^1-\dfrac{n}{n+1}\int_0^1(-x)^n\ln(x)^{n-1}\ud
x\\
&&\\
&=&- \dsp \dfrac{n}{n+1}\int_0^1(-x)^n\ln(x)^{n-1}\ud x=\cdots\\
&=& \dsp \dfrac{n!}{(n+1)^n}\int_0^1x^n\ud x
\end{array}$$
Ce qui donne
$$\int_0^1(-x\ln(x))^n\ud x=\dfrac{n!}{(n+1)^{n+1}}\Longrightarrow \int_0^1x^{-x}\ud x=
\dsum_{n\geq 0}\dfrac{1}{n!}\dfrac{n!}{(n+1)^{n+1}}\Longrightarrow\boxed{\int_0^1x^{-x} \ud x =
\dsum_{n\geq 1}\dfrac{1}{n^n}}.$$
Donner le domaine de définition de $S(x)=\dsum_{n\geq 1}\frac{\cos(nx)}{2^n}$ puis exprimer $S$ à l'aide des fonctions usuelles.
Pour tout $x\in \R$, on a $\abs{\frac{\cos(nx)}{2^n}}\leq \frac{1}{2^n}$ comme $\dsum \frac{1}{2^n}$
CV, on en déduit que $\dsum_{n\geq 1}\frac{\cos(nx)}{2^n}$ est normalement convergente sur $\R$.
Notons $S$ sa somme.
Pour tout $x\in \R$, on a $\dfrac{\cos(nx)}{2^n}=\re \left(\dfrac{\ee^{\ii n x}}{2^n}\right)=\re
\left( \left(\frac{\ee^{\ii x}}{2}\right)^n\right)$. Ce qui donne,
$$ S(x)=\re \left(\dsum_{n\geq 0} \left(\frac{\ee^{\ii x}}{2}\right)^n\right)-1=\re
\dfrac{2}{2-\ee^{\ii x}} -1=\dfrac{4-2\cos
x}{5-4\cos(x)}-\dfrac{5-4\cos(x)}{5-4\cos(x)}=\boxed{\dfrac{2\cos(x)-1}{5-4\cos(x)}}.$$
Soit $(a_n)_n$ une suite de nombre complexe telle que, pour tout $n\in \N$, $\abs{a_n}\leq 1$. On définit, pour $n\in \N$, l'application $f_n:\R\longmapsto\C$ par $f_n(x)=a_n\ee^{-\abs{x-n}}$.
- Étudier la CS de $\dsp\sum f_n$
- Montrer que $\forall x\in\R,~~\dsp\abs{\sum_{n=0}^\infty f_n(x)}\leq \dfrac{2\ee}{\ee -1}$
- Soit $x\in \R$, on a
$\abs{f_n(x)}\underset{n\rightarrow\infty}{\thicksim}\abs{a_n}\ee^{-n+x}$,
comme $\dsum \abs{a_n}\ee^{-n+x}$ converge, on en déduit que $\dsum f_n(x)$ est absolument
convergente donc
convergente.
Ce qui donne $\dsum f_n$ converge simplement sur $\R$. - Soit $x\in \R$,
- Si $x\leq 0$ alors $\abs{\dsum_{n\geq 0}f_n(x)}\leq \dsum_{n\geq 0}\ee^{-n}=\dfrac{\ee}{\ee-1}\leq \dfrac{2\ee}{\ee -1}$.
- Si $x\geq 0$ alors en notant $N=\mathrm{E}(x)$, on a $\abs{\dsum_{n\geq 0}f_n(x)}\leq \dsum_{n=0}^N\ee^{-x+n}+\dsum_{n\geq N+1}\ee^{x-n}$, puis $$\dsum_{n=0}^N\ee^{-x+n}+\dsum_{n\geq N+1}\ee^{x-n}=\ee^{-x}\dfrac{\ee^{N+1}-1}{\ee-1}+\ee^{x-(N+1)} \dfrac{\ee}{\ee-1}\leq \dfrac{\ee^{N+1-x}}{\ee-1}+\dfrac{\ee^{x-N}}{\ee -1}\leq \dfrac{\ee}{\ee-1}+\dfrac{\ee}{\ee -1}= \dfrac{2\ee}{\ee -1}$$
On pose, pour tout $n\in\N^*$ et tout $x\in\R_+$ : $\displaystyle f_n(x)=\frac{\ee^{-nx}}{(n+x)^2}$.
- Étudier la convergence de la série $\sum f_n$ sur~$\R_+$.
- Étudier la continuité de sa somme $S$.
- Montrer que $S$ est positive et décroissante sur~$\R_+$.
- Que vaut $S(0)$ ? Calculer $\lim\limits_{x\to\infty} S(x)$.
- Montrer que $S$ est de classe~$\CC^1$ sur $]0,+\infty[$.
- Montrer qu'elle est convexe. HP
- $S$ est-elle dérivable en~$0$ ?
-
Soit $n\geq 1$, on a $f_n\in \CC^\infty (\R_+,\R)$ de plus,
$$\forall x\geq 0,\quad f_n'(x)=\dfrac{-\ee^{-nx}}{(n+x)^3}(n(n+x)+2)< 0\Longrightarrow
f_n(x)\leq f_n(0)=
\norme{f_n}_\infty^{\R_+}=\dfrac{1}{n^2}.$$
Comme la série $\dsum \dfrac{1}{n^2}$ converge, on en déduit: $\dsum_n f_n$ converge normalement
sur $\R_+$.
Ce qui implique la converge simple et uniforme de $\dsum f_n$ sur $\R_+$. - Les fonctions $f_n$ sont continue sur $\R_+$ et la convergence de $\dsum_{n\geq 1}f_n$ vers $S$ est uniforme, on en déduit que $S$ est continue sur $\R_+$.
-
$\boxed{S(0)=\dsum_{n\geq 1}\dfrac{1}{n^2}=\dfrac{\pi^2}{6}}$.
D'autre part, pour tout $n\geq 1,\,\limiteX{x}{\infty}f_n(x)=0$, étant donnée que la série $\dsum_nf_n$ converge uniformément on en déduit $\boxed{\lim\limits_{x\to\infty} S(x)=\dsum_{n\geq 1}\lim\limits_{x\to\infty} f_n(x)=0}$. -
Soit $a>0$, pour tout $x\in [a,\infty[$, on a:
$$\abs{f_n'(x)}=\dfrac{\ee^{-nx}(n(n+x)+2)}{(n+x)^3}\leq
\dfrac{n\ee^{-na}}{(n+a)^2}+\dfrac{1}{(n+a)^3}\Longrightarrow\norme{f_n}_\infty^{[a,\infty[}\leq
\dfrac{n\ee^{-na}}{(n+a)^2}+\dfrac{1}{(n+a)^3}.$$
Comme les séries $\dsum \dfrac{n\ee^{-na}}{(n+a)^2}$ et $\dsum\dfrac{1}{(n+a)^3}$ sont
convergente donc
$\dsum f_n'$ est normalement convergente sur $[a,\infty[$.
Ceci assure la convergence simple de $\dsum f_n'$ sur $]0,\infty[$ de plus cette convergence est uniforme locale. On en déduit que $S$ est de classe $\CC^1$ sur $]0,\infty[$ et pour tout $x>0$,$\,\,S'(x)=\dsum_{n\geq 1}f_n'(x)$.
Soit $f:]-1,1[\longmapsto \C$ une application continue. On définit la suite de fonctions $(f_n)_n$ par: $$f_0=f,~~\forall n\geq 0,~~\forall x\in ]-1,1[,~~f_{n+1}(x)=\int_0^xf_n(t)\ud t.$$ Montrer que la série de fonction $\dsp\sum f_n$ est convergente sur $]-1,1[$, puis calculer $\dsp\sum_{n\geq 0} f_n$ en fonction de $f$.
On montre par récurrence sur $n\in \N$ que $f_n$ est bien définie et que $f_n$ est de classe $\CC^1$
pour $n\geq 1$.
De plus, pour $a\in ]0,1[$, on a
$\norme{f_{n+1}}_{\infty}^{[-a,a]}\leq a\norme{f_{n}}_{\infty}^{[-a,a]}$, ce qui donne
$$\forall n\in \N,~~\norme{f_{n}}_{\infty}^{[-a,a]}\leq a^n\norme{f}_{\infty}^{[-a,a]}$$
comme la série $\dsum a^n \norme{f}_{\infty}^{[-a,a]}$ est convergente, on en déduit que $\dsum f_n$
est normalement convergente sur $[-a,a]$.
Ce qui donne $\dsum f_n$ est uniformément localement convergente sur $]-1,1[$.
Notons $G=\dsum_{n\geq 0}f_{n+1}$, $G$ est bien définie, de plus comme $f_{n+1}'=f_n$ et que
$\dsum f_n$ converge localement uniformément sur $]-1,1[$, le théorème de dérivation terme à terme
d'une série de fonction montre que $G$ est de classe $\CC^1$ sur $]-1,1[$ et que
$$G'=\dsum_{n\geq 0}f_n=f+G\Longrightarrow G'-G=f,\text{ et }G(0)=0.$$
La résolution de cette équation différentielle nous donne $G(x)=\ee^{x}\dsp \int_0^x\ee^{-t}f(t)\ud
t$,
d'où
$$\forall x\in ]-1,1[,~~~~\sum_{n\geq 0}f_n(x)=f(x)+\ee^x\int_0^x\ee^{-t}f(t)\ud t.$$
On considère la suite de fonction $\fonct{f_n}{[0,\pi/2]}{\R}{x}{x\sin(x)\cos(x)^n}$.
Étudier la suite $(f_n)$, puis la série $\dsum f_n$.
- $\boxed{f_n\overset{C.U}{\tendversN}0}$ sur $\left[0,\frac{\pi}{2}\right]$.
-
Pour $x=0$, on a $f_n(0)=0$ donc $\dsum f_n(0)$ converge et vaut $0$. Soit $x\in
]0,\frac{\pi}{2}]$,
et $n\in \N^*$, on a
$$\dsum_{k=0}^nf_k(x)=\dsum_{k=0}^nx\sin(x)\cos^k(x)=x\sin(x)\dfrac{1-\cos(x)^{n+1}}{1-\cos(x)}\tendversN\dfrac{x\sin(x)}{1-\cos(x)}.$$
On en déduit que $\dsum f_n\overset{C.U}{\tendversN}f$ avec $f(x)=\left\{\begin{array}{ll}
0&\text{ si }x=0\\
\dfrac{x\sin(x)}{1-\cos(x)}
\end{array}
\right.$ .
La fonction $g$ n'est pas continue en $0$, car, pour $x\in ]0,\frac{\pi}{2}]$, on a $$g(x)=\dfrac{x^2+\mathrm{o}(x^3)}{1-(1-\frac{x^2}{2}+\mathrm{o}(x^2))}=2+\mathrm{o}(x)\tendvers{x}{0^+}2\neq g(0).$$ Donc $\dsum f_n$ ne converge pas uniformément sur $[0,\frac{\pi}{2}]$.
Soit la fonction $f$ définie par $f(x)=\dsum_{n\geq 1} \dfrac{\ln \left(n+\ee^{nx}\right)} {n^3}$. Montrer que $f$ est définie sur $\R$, puis $f\in \CC^1(\R)$.
Pour $n\geq 1$ et tout $x\in \R$, on a $n+\ee^{nx}>0$ donc $\ln \left(n+\ee^{nx}\right)$ est définie.
On pose $f_n(x)=\dfrac{\ln \left(n+\ee^{nx}\right)}{n^3}$, $f_n\in \CC^1(\R)$.
Pour $x\leq 0$, on a $f_n(x)\underset{n\to\infty}{\thicksim}\dfrac{\ln(n)}{n^3}$, comme la série
$\dsum \frac{\ln (n)}{n^3}$ converge alors $\dsum f_n(x)$ converge.
Pour $x>0$, on a $f_n(x)\underset{n\to\infty}{\thicksim}\dfrac{\ln(\ee^{nx})}{n^3}=\dfrac{x}{n^2}$,
on sait que la série $\dsum \frac{x}{n^2}$ converge, il en va de même pour $\dsum f_n(x)$.
On en déduit que $\dsum f_n$ est définie sur $\R$ et $\dsum f_n$ converge simplement vars $f$.
Pour montrer que $f\in \CC^1(\R)$, il faut montrer que $\dsum f_n'$ converge uniformément localement
sur $\R$. Pour tout $n\in \N^*$ et $x\in \R$, on a $f_n'(x)=\dfrac{ \ee^{nx}}{n^2(n+\ee^{nx})}.$ En
particulier, on a:
$$\forall x\in \R, 0< f_n'(x)\leq \dfrac{1}{n^2}\Longrightarrow \norme{f_n'}_\infty\leq
\dfrac{1}{n^2}\Longrightarrow\dsum_{n\geq 1}\norme{f_n}_\infty \text{ CV}.$$
Donc $\dsum f_n'$ est normalement convergente donc uniformément sur $\R$. On en déduit,
$$\boxed{f\in \CC^1(\R),\quad \forall x\in
\R,\,\,f'(x)=\dsum_{n=1}^\infty\dfrac{1}{n^2}\dfrac{\ee^{nx}}{n+\ee^{nx}}}.$$
Pour $n\in \N^*$, on définit $f_n$ sur $\R$ par $f_n(x)=\frac{1}{n}\Arctan\left(\frac{x}{n}\right)$.
- Montrer que la série de fonctions $\dsum_n f_n$ converge simplement sur $\R$ et que sa somme $S$ est continue sur $\R$.
- Justifier l'existence d'une limite, éventuellement infinie, pour $S(x)$ lorsque $x$ tend vers $\infty$.
-
Pour tout $x\in \R^*$, on a
$\frac{1}{n}\Arctan\left(\frac{x}{n}\right)\underset{n\to \infty}{\thicksim}\dfrac{x}{n^2}$,
comme $\dsum \dfrac{x}{n^2}$ converge, on en déduit que $\dsum f_n(x)$ converge et ceci reste
vraie
pour $x=0$, autrement dit, $\dsum f_n$ est définit pour tout $x\in \R$ et donc converge
simplement
sur $\R$ vers $S$ (sa somme).
La convergence n'est pas normale sur $\R$, puisque $\norme{f_n}_\infty=\dfrac{\pi}{2n}$ et $\dsum \dfrac{\pi}{2n}$ diverge. En revanche, pour tout $A\in \R_+^*$, on a $\norme{f_n}_\infty^{[-A,A]}=\dfrac{1}{n}\Arctan\left(\frac{A}{n}\right)$ et donc $\dsum f_n$ converge normalement sur $[-A,A]$. Ceci prouve que $\dsum f_n$ converge uniformément sur tout segment de $\R$, et puisque les $f_n$ sont continues on en déduit alors que $S$ est continue sur $\R$. -
On a $f_n\in \CC^1(\R)$ et
$$\forall x\in \R,\quad
f_n'(x)=\dfrac{1}{n^2+x^2}\Longrightarrow\norme{f_n'}_\infty=\dfrac{1}{n^2}
\Longrightarrow \dsum_{n\geq 1}\norme{f_n'}_\infty< \infty.$$
Donc $\dsum f_n'$ converge uniformément sur $\R$ ce qui prouve que $S$ est de classe $\CC^1$ sur
$\R$, de plus,
$S'(x)=\dsum_{n\geq 1}\dfrac{1}{n^2+x^2}>0$, donc $f$ est strictement croissante sur $\R$.
La croissance de $S$ sur $\R$ prouve que $S$ admet une limite en $\infty$ (éventuellement $\infty$). D'autre part, on a pour tout $N>1$, $$\forall x>0,\quad S(x)=\dsum_{n\geq 1}\frac{1}{n}\Arctan\left(\frac{x}{n}\right)>\dsum_{n=1}^N\frac{1}{n} \Arctan\left(\frac{x}{n}\right)$$ donc $$\limiteX{x}{\infty}S(x)\geq \limiteX{x}{\infty}\left(\dsum_{n=1}^N\frac{1}{n}\Arctan\left(\frac{x}{n}\right)\right)=\dsum_{n=1}^N\frac{\pi}{2n}.$$ Ceci étant vraie pour tout $N\geq 1$, en faisant tendre $N$ vers $\infty$ et compte tenu que $\dsum \dfrac{1}{n}$ diverge, on conclut que $\dsp\limiteX{x}{\infty}S(x)=\infty$.
- Déterminer le domaine de définition de $\dsp f(x)=\dsum_{n\geq 1}\frac{1}{n}\cos(x)^n\sin(nx)$.
- Montrer que $f$ est de classe $\CC^1$ sur $\R\setminus\pi\Z$, puis calculer $f'$. En déduire $f$
-
Notons, pour $n\in N^*$, $\fonct{f_n}{\R}{\R}{x}{\frac{1}{n}\cos^n(x)\sin(nx)}$. On a
- Pour $x\in \pi\Z$, $\sin(nx)=0$ donc $f_n(x)=0$ et $\dsum f_n(x)$ converge.
- Pour $x\in \R\setminus \pi\Z$, $\abs{\cos(x)}< 1$ et $\abs{f_n(x)}\leq \dfrac{\abs{\cos(x)}^n}{n}\leq \abs{\cos(x)}^n$, donc $\dsum f_n(x)$ est absolument convergente puisque $\dsum \abs{\cos(x)}^n$ converge.
- D'après la remarque précédente, il suffit de réduire l'étude sur $[0,\pi]$.
Pour tout $n\in \N^*$, $f_n\in \CC^1(\R)$ et $f_n'(x)=-\cos^{n-1}(x)\sin(x)\sin(nx)+\cos^n(x)\cos(nx)=\cos^{n-1}(x)\cos((n+1)x)$.
Pour $a\in ]0,\pi/2[$, et pour tout $x\in [a,\pi-a]$, on a $\norme{f_n'}_\infty^{[a,\pi-a]}\leq \abs{\cos(a)}^{n-1}$ donc $\dsum f_n'$ converge normalement sur $[a,\pi-a]$, ce qui implique que $\dsum f_n'$ converge uniformément localement sur $]0,\pi[$ donc $f\in \CC^1(]0,\pi[)$. De plus $$\begin{array}{lcl} \forall x\in ]0,\pi[,\quad f'(x)&=&\dsum_{n\geq 1}\cos^{n-1}(x)\cos((n+1)x)=\dsum_{n\geq 1}\cos^{n-1}(x)\re \left(\ee^{\ii (n+1)x}\right)\\ &=&\re \left(\ee^{2\ii x}\dsum_{n\geq 1}\left(\cos(x)\ee^{\ii x}\right)^{n-1}\right)=\re \left(\ee^{2\ii x}\dsum_{n\geq 0}\left(\cos(x)\ee^{\ii x}\right)^{n}\right)\\ &=&\re \left(\dfrac{\ee^{2\ii x}}{1-\cos(x)\ee^{\ii x}}\right)=\re \left(\dfrac{\ee^{\ii x}}{\ee^{-\ii x}-\cos(x)}\right)=-1 \end{array} $$ - Comme $f$ est de classe $\CC^1$ sur $]0,\pi[$ et $f'=-1$, on en déduit que: $$\forall x\in ]0,\pi[,\quad f(x)=C-x,\quad \text{ comme }f(\pi/2)=0 \Longrightarrow \forall x\in ]0,\pi[,\quad f(x)=\dfrac{\pi}{2}-x\quad\text{ et }f(0)=f(\pi)=0.$$ Ensuite, on complète sur $\R$ en utilisant le faite que $f$ est impaire et $\pi$-périodique.
Remarque On a $f$ n'est pas continue sur $\R$.
- Déterminer le domaine de définition de $\dsp f(x)=\dsum_{n\geq 0}(-1)^n \dfrac{\ee^{-nx}}{n+1}$.
- Montrer que $f\in \CC(\R_+,\R)$ et $f\in \CC^1(\R_+^*,\R)$.
- Déterminer une équation différentielle simple dont $f$ est solution et en déduire que $f$ est de classe $\CC^1$ sur $[0, \infty[$.
-
On définit pour $n\in \N,\,x\in \R,\quad u_n(x)=(-1)^n\dfrac{\ee^{-nx}}{n+1}$.
- Pour $x< 0$, on a $\abs{u_n(x)}\tendversN\,\infty$. Donc $\dsum u_n(x)$ diverge.
- Pour $x=0$, on $\dsum u_n(0)$ converge (CSSA).
- Pour $x>0$, on a $$\abs{u_n(x)}=\dfrac{\ee^{-nx}}{n+1}\leq \ee^{-nx},\text{ et } \dsum_{n\geq 0}\ee^{-nx} \text{ converge}\Longrightarrow \dsum_{n\geq 0} \abs{u_n(x)}\text{ converge}.$$ On en déduit que $\dsum_{n\geq 0} \abs{u_n(x)}$ converge.
- Les fonctions $u_n$ sont continue, on en déduit que la somme est continue sur $\R_+$.
D'autre part, pour tout $n\geq 0$, $u_n\in \CC^1(\R_+)$ et $u_n'(x)=(-1)^{n+1}\dfrac{n}{n+1}\ee^{-nx}$. Donc $$\dsum u_n'(0)\text{ diverge car } (-1)^{n+1}\dfrac{n}{n+1} \text{ ne tend pas vers }0 \text{ lorsque } n \text{ tend vers }\infty.$$ Soit $a>0$, on a $$\forall x\geq a,\,\abs{u_n'(x)}=\dfrac{n}{n+1}\ee^{-nx}\leq \ee^{-na}\Longrightarrow\norme{u_n'}_\infty^{[a,\infty[}\leq \ee^{-na}$$ Comme $\dsum \ee^{-na}$ converge, on en déduit que $\dsum u_n'$ converge normalement sur $[a,\infty[$, donc $S\in \CC^1([a,\infty)$, et pour tout $x\geq a,\,S'(x)=\dsum_{n\geq 0} (-1)^{n+1}\dfrac{n}{n+1}\ee^{-nx}.$
La dérivabilité s'étend à $\R_+$ puisque $a$ est un réel strictement positif quelconque. -
Pour tout $x>0$, on a
$$S'(x)=\dsum_{n\geq 0} (-1)^{n+1}\dfrac{n\textcolor{red}{+1-1}}{n+1}\ee^{-nx}=\dsum_{n\geq 0}
-(-\ee^{-x})^n+\dsum_{n\geq 0} (-1)^{n+1}\dfrac{\ee^{-nx}}{n+1}=\dfrac{-1}{1+\ee^{-x}}+S(x).$$
Comme $S$ est continue en $0$, on en déduit que $S'$ admet une limite finie en $0$ et
$\lim_{x\to 0^+}S'(x)=S(0)-\dfrac{1}{2}$.
D'autre part, on a pour tout $n>1$, $u_n(x)\tendvers{x}{\infty}0$ et $u_0(x)\tendvers{x}{\infty}1$. La converge étant uniforme, on en déduit que $S(x)\tendvers{x}{\infty}1$.
Ainsi $S$ est l'unique solution du problème de Cauchy suivant: $$y'-y=\dfrac{-1}{1+\ee^{-x}},\quad \text{et }\lim_{x\to \infty}y(x)=1.$$ La résolution de ce problème donne: $$\forall x>0,\,\,(y\ee^{-x})'=\dfrac{-\ee^{-x}}{1+\ee^{-x}}\Longrightarrow \forall x>0,\quad\,y(x)=\alpha\ee^x+\ee^x\ln\left(1+\ee^{-x}\right).$$ Avec $\alpha\in\R$, en utilisant la limite en $\infty$, on trouve $\alpha=0$, on en déduit, $\boxed{\forall x>0,\,\,S(x)=\ee^x \ln\left(1+\ee^{-x}\right)}.$
La continuité de $S$ en $0$, permet de prolonger la relation précédent sur $\R_+$, on retrouve également que $S$ est de $\CC^1$ sur $\R_+$.
On considère la fonction $f(x)=\dsum_{n\geq 1}\frac{\ee^{-nx}}{n^2}$
- Montrer que $f$ est définie et continue sur $\R_+$.
- Montrer que $f$ est de classe $\CC^1$ puis $\CC^2$ sur tout intervalle $[a,\infty[$ où $a>0$.
- $f$ est-elle dérivable en $0$?
-
Notons, pour $n\geq 1$, $f_n(x)=\dfrac{\ee^{-nx}}{n^2}$, il est clair que $f_n\in
\CC^\infty(\R)$.
- Pour $x< 0$, on a $f_n(x)\tendversN\infty$ donc $\dsum f_n(x)$ diverge.
- Sur $\R_+$, on a $\norme{f_n}_\infty^{\R_+}=\dfrac{1}{n^2}$, donc $\dsum f_n$ converge normalement sur $\R_+$
- Soit $a>0$, on a pour tout $x\in [a,\infty[$, $$f_n'(x)=\dfrac{-\ee^{-nx}}{n},\quad \norme{f_n'}_\infty^{[a,\infty[}=\dfrac{\ee^{-na}}{n},\quad f_n''(x)=\ee^{-nx},\quad \norme{f_n''}_\infty^{[a,\infty[}=\ee^{-na}.$$ Comme les séries $\dsum \dfrac{\ee^{-na}}{n}$ et $\dsum \ee^{-na}$ sont convergentes, on en déduit que $\dsum f_n'$ et $\dsum f_n''$ sont normalement convergentes sur $[a,\infty[$, ceci prouve que $f\in \CC^2(\R_+^*)$. De plus, $$\forall x>0,\quad f'(x)=\dsum_{n\geq 1}\dfrac{-\ee^{-nx}}{n},\quad f''(x)=\dsum_{n\geq 1}\ee^{-nx}=\dfrac{1}{1-\ee^{-x}}-1=\dfrac{\ee^{-x}}{1-\ee^{-x}}.$$
-
En intégrant la relation obtenue pour $f''$, on trouve:
$\forall x>0,\quad f'(x)=\ln\left(1-\ee^{-x}\right)+K,\,\,K\in \R$.
Pour trouver la valeur de $K$, on utilise la convergence uniforme de $\dsum f_n'$ sur $[1,\infty[$, ce qui donne $$\limiteX{x}{\infty}f'(x)=\dsum_{n\geq 1}\limiteX{x}{\infty}f_n'(x)=0=\limiteX{x}{\infty}\left(\ln\left(1-\ee^{-x}\right)+K\right)=K\Longrightarrow \forall x>0,\quad f'(x)=\ln\left(1-\ee^{-x}\right).$$ La relation précédente montre que $\dsp\limiteX{x}{0^+}f'(x)=-\infty$ donc $f$ n'est pas dérivable en $0$.
Montrer que la fonction $f$ définie par $f(x)=\dsum_{n\geq 1} (-1)^n\dfrac{n}{n^2+x^2}$ est de classe $\CC^\infty$ sur $\R$.
Montrons d'abord que $f$ est définie sur $\R$. On a, pour tout $x\in \R$:
- $\dfrac{n}{n^2+x^2}\tendversN\,0$
- ] La suite $\left(\dfrac{n}{n^2+x^2}\right)$ est décroissant à partir d'un certain rang, en effet, si on pose $g(t)=\dfrac{t}{t^2+x^2}$ alors $g'(t)=\dfrac{x^2-t^2}{(t^2+x^2)^2}$ donc strictement négative sur $]\abs{x},\infty[$.
Donc d'après CSSA, $\dsum_{n\geq 1} (-1)^n\dfrac{n}{n^2+x^2}$ converge, ce qui prouve que $f$ est
définie sur $\R$.
D'autre part, si on pose $f_n(x)= (-1)^n\dfrac{n}{n^2+x^2}$, alors $f_n\in \CC^\infty(\R)$, et on a
$$\forall x\in \R,\quad f_n(x)=\dfrac{a}{x+\ii n}+\dfrac{b}{x-\ii n} =
\dfrac{(-1)^n\ii}{2}\left(\dfrac{1}{x+\ii n}-\dfrac{1}{x-\ii n}\right).$$
Donc pour tout $p\geq 1$, et pour tout $x\in \R$,
$$f^{(p)}(x)=\dfrac{(-1)^n\ii}{2}\left(\dfrac{(-1)^pp!}{(x+\ii n)^{p+1}}-
\dfrac{(-1)^pp!}{(x-\ii n)^{(p+1)}}\right)$$
donc$$
\abs{f^{(p)}(x)}\leq \dfrac{1}{2}\left(\dfrac{p!}{n^{p+1}}+\dfrac{p!}{n^{p+1}}\right)\leq
\dfrac{p!}{n^{p+1}}\Longrightarrow \norme{f^{(p)}}_\infty\leq \dfrac{p!}{n^{p+1}}$$
La série $\dsum \dfrac{p!}{n^{p+1}}$ converge, on en déduit que $\dsum f^{(p)}$ est normalement
convergente sur $\R$.
Soit $n\in \N^*$. On définit $f_n$ sur $\R_+^*$ par $\dsp f_n(x)=\dfrac{n^x\,n!}{\prod_{0\leq k\leq n}(x+k)}$.
- Prouver l'existence, pour tout $x>0$ de $\Gamma(x)= \limiteX{n}{\infty}f_n(x)$.
- Montrer l'existence d'une constante $\gamma$ telle que : $\dsp\forall x>0,\quad \ln (\Gamma(x))=-\ln(x)-\gamma x+\dsum_{n\geq 0} \left(\dfrac{x}{n}-\ln\left(1+\frac{x}{n}\right)\right).$
- Montrer que $\Gamma$ est de classe $\CC^1$ sur $\R_ +^*$.
- Comme $f_n$ est strictement positive, on considère alors $\ln(f_n)$. Soit $x>0$, on a $$\ln(f_n(x))=x\ln(n)+\ln(n!)-\dsum_{k=0}^n\ln(x+k),$$ ce qui donne: $$\forall n\geq 2,\,\ln(f_{n}(x))-\ln(f_{n-1}(x))= -x\ln(1-\frac{1}{n})+\ln(n)-\ln(x+n).$$ Soit, $$\ln(f_{n}(x))-\ln(f_{n-1}(x))=\dfrac{x}{n}+\mathrm{O}\left(\frac{1}{n^2}\right) +\ln(n)-\ln(n)- \ln(1+\frac{x}{n})=\mathrm{O}\left(\frac{1}{n^2}\right)$$ Autrement dit, la série $\dsum_{n\geq 2} \left(\ln(f_n(x))-\ln(f_{n-1}(x))\right)< \infty$. On en déduit que $\ln(f_n(x))\tendversN \ell (x)\in \R$, soit $f_n(x)\tendversN\ee^{\ell (x)}=\Gamma(x)$.
-
Soit $x>0$, pour tout $n\geq 1$, on a
$$\begin{array}{lcl}
\ln(f_n(x))&=&x\ln(x)+\ln(n!)-\dsum_{k=0}^n\ln(x+k)\\
&=&x\ln(n)+\dsum_{k=1}^n\ln(k)-\dsum_{k=0}^n\ln(x+k)\\
&=&x\ln(x)-\dsum_{k=1}^n\ln\left(1+\frac{x}{k}\right)-\ln(x)\\
&=&-\ln(x)+x\left(\ln(n)-\dsum_{k=1}^n\frac{1}{k}\right)+\dsum_{k=1}^n\left(\frac{x}{k}-\ln\left(1+\frac{x}{k}\right)\right)
\end{array}$$
Or, la suite $\ln(n)-\dsum_{k=1}^n\frac{1}{k}$ converge dans $\R$ vers $-\gamma$ (avec
$\gamma>0$) et la série
$\dsum_{k=1}^n\left(\frac{x}{k}-\ln\left(1+\frac{x}{k}\right)\right)$ converge également puisque
$\dfrac{x}{k}-\ln\left(1+\dfrac{x}{k}\right)=\underset{n\to\infty}{\mathrm{O}}\left(\frac{x}{n^2}\right)$.
Comme $(\ln(f_n(x)))$ converge également dans $\R$ d'après la question précédente, on en déduit, $$\limiteX{n}{\infty}\ln(f_n(x))= \limiteX{n}{\infty}-\ln(x)+x\left(\ln(n)-\dsum_{k=1}^n\frac{1}{k}\right)+\dsum_{k=1}^n\left(\frac{x}{k}-\ln\left(1+\frac{x}{k}\right)\right),$$ ce qui donne, $$\ln(\Gamma(x))=-\ln(x)-\gamma x+\dsum_{k\geq 1}\left(\frac{x}{k}-\ln\left(1+\frac{x}{k}\right)\right).$$ - Il faut juste montrer que $x\longmapsto \dsum_{k\geq 1}\left(\frac{x}{k}-\ln\left(1+\frac{x}{k}\right)\right)$ est de classe $\CC^1$ sur $\R_+^*$.
On définit pour $n\in \N$, $f_n(x)=nx\ee^{-nx^2}$.
- Montrer que $\dsum f_n$ converge normalement sur tout segment de $\R^*$. On note $S$ sa somme, montrer que $S$ est impaire.
- Soit $a>0$. Calculer pour $x>0$, $\dsp\int_a^x S(t)\ud t$ et en déduire $S$.
-
Soit $0< a< b< \infty$, on considère le segment $[a,b]\subset\R_+^*$. On a
$$\forall n\in \N,\quad\forall x\in [a,b],\quad \abs{f_n(x)}\leq
nb\ee^{-na^2}\Longrightarrow\norme{f_n}_\infty^{[a,b]}\leq nb\ee^{-na^2}.$$
Comme $\dsum nb\ee^{-na^2}$ converge, alors $\dsum \norme{f_n}_\infty^{[a,b]}$ converge, donc la
série
$\dsum f_n$ converge normalement sur $[a,b]$.
Soit maintenant $-\infty < a < b < 0$, alors, pour tout $x\in [a,b]\subset\R_-^*$, on a $\abs{f_n(x)}\leq n\abs{a}\ee^{-nb^2}$, donc $\norme{f_n}_\infty^{[a,b]}\leq n\abs{a}\ee^{-nb^2}$ ce qui prouve aussi la convergence normale de $\dsum f_n$ sur $[a,b]$.
Le raisonnement précédent montre la convergence normale de $\dsum f_n$ sur tout segment de $\R^*$, donc $\dsum f_n$ converge uniformément localement sur $\R^*$, ce qui implique aussi la convergence simple sur $\R^*$. Notons $S$ sa somme.
On a également, pour tout $n\in \N$, $f_n(0)=0$, donc $\dsum f_n(0)$ converge ce qui donne $S$ est définie en $0$ et $S(0)=0$.
On a, pour tout $n\in \N$ et $x\in \R$, $f_n(-x)=-nx\ee^{-nx^2}=-f_n(x)$, on en déduit, $$\forall x\in \R,\quad S(-x)=\dsum_{n\geq 0}f_n(-x)=-\dsum_{n\geq 0}f_n(x)=-S(x)\Longrightarrow S \text{ est impaire}.$$ - Soit $a>0,\,x>0$, comme $\dsum f_n$ converge uniformément sur $[a,x]$ (où $[x,a]$ si $x< a$), alors, $$\int_a^xS(t)\ud t=\dsum_{n\geq 0}\int_a^xnt\ee^{-nt^2}\ud t=\dsum_{n\geq 0}\left[\dfrac{-\ee^{-nt^2}}{2}\right]_a^x= \dsum_{n\geq 0}\dfrac{\ee^{-na^2}-\ee^{-nx^2}}{2}=\dfrac{1}{2}\left(\dfrac{1}{1-\ee^{-a^2}}-\dfrac{1}{1-\ee^{-x^2}}\right).$$ La fonction $f:x\in \R_+^*\longmapsto \dsp\int_a^xS(t)\ud t$ est une primitive de $S$ sur $\R_+^*$. On en déduit, $$\forall x>0,\quad S(x)=f'(x)=\dfrac{1}{2}\dfrac{2x\ee^{-x^2}}{(1-\ee^{-x^2})^2} =\dfrac{x\ee^{-x^2}}{(\ee^{-x^2})^2(\ee^{x^2/2}-\ee^{-x^2/2})^2}=\dfrac{x}{4\sh^2\left(\frac{x^2}{2}\right)}.$$
On considère la fonction f définie sur un ensemble $D_{f}$ et donnée par
$f : x \mapsto \displaystyle \sum _{n = 1}^{\infty} \frac{(-1)^{n-1}}{\ln(nx)}$.
Trouver $D_{f}$, puis montrer la continuité de cette fonction sur $]1;+\infty[$.
Quelle est sa limite en $1$ ? En $+\infty$ ?
%
Calculer $$\mathbf{1.}\,\limiteX{x}{1}\dsum_{n=1}^\infty\dfrac{x^2}{(n+x)^2},\quad\quad\mathbf{2.}\, \limiteX{x}{\infty}\dsum_{n=1}^\infty \dfrac{\ee^{-nx}}{n^2},\quad\quad\mathbf{3.}\,\limiteX{x}{0^+}\dsum_{n=1}^\infty \dfrac{\ee^{-nx}}{n^2}.$$
- Pour $n\geq 1$, on pose $f_n(x)=\dfrac{x^2}{(n+x)^2}$, on a $$\forall x\in [0,2],\quad 0\leq f_n(x)\leq \dfrac{4}{n^2}\Longrightarrow \norme{f_n}_\infty^{[0,2]}\leq \dfrac{2}{n^2},$$ on en déduit que $\dsum f_n $ converge normalement sur $[0,2]$, comme les $f_n$ sont continues, on en déduit que la fonction somme est continue, ce qui donne $$\limiteX{x}{1}\dsum_{n=1}^\infty\dfrac{x^2}{(n+x)^2}=\dsum_{n=1}^\infty\dfrac{1}{(n+1)^2}=\dsum_{n=2}^\infty\dfrac{1}{n^2}=\dfrac{\pi^2}{6}-1.$$
- Pour $n\geq 1$, on pose $f_n(x)=\dfrac{\ee^{-nx}}{n^2}$, il est clair que $f_n\in \CC(\R_+)$, d'autre part, $$\forall x\geq 0,\quad\, 0\leq f_n(x)\leq \dfrac{1}{n^2}\Longrightarrow\norme{f_n}_\infty^{\R_+}\leq \dfrac{1}{n^2}\Longrightarrow \dsum f_n \text{ C N sur } \R_+.$$ D'après le cours, et puisque $f_n(x)\tendvers{x}{0^+}\dfrac{1}{n^2}$ et $f_n(x)\tendvers{x}{\infty}\,0$, on trouve: $$\limiteX{x}{\infty}\dsum_{n=1}^\infty \dfrac{\ee^{-nx}}{n^2}=0,\quad \limiteX{x}{0^+}\dsum_{n=1}^\infty \dfrac{\ee^{-nx}}{n^2}=\dsum_{n\geq 1}\frac{1}{n^2}=\frac{\pi^2}{6}.$$
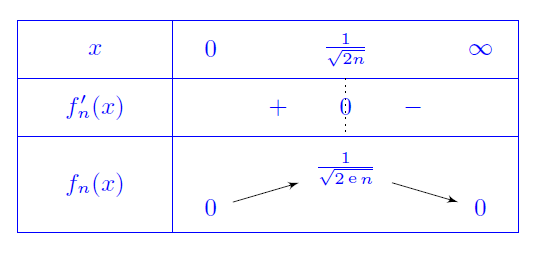
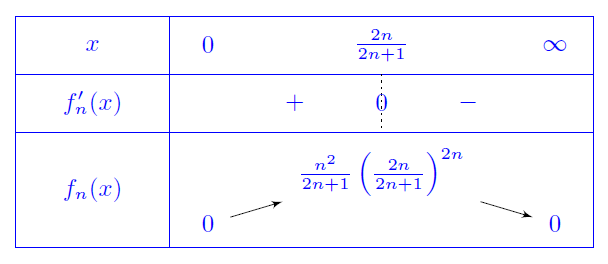
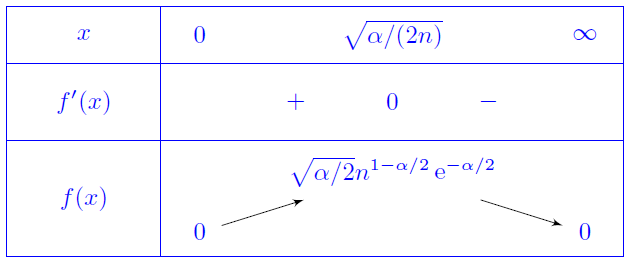
On considère la suite de fonctions $(f_n)$ définie, sur $\R_+^*$, par
$f_n(x)=nx^\alpha\ee^{-nx^2}$.
Étudier, selon les valeurs de $\alpha\in \R_+^*$, la convergence de la série de fonction $\dsum f_n$.
Pour tout $x>0$, on a $n^2f_n(x)\tendversN\, 0$ donc
$f_n(x)=\underset{n\to\infty}{\mathrm{o}}\left(\frac{1}{n^2}\right)$. On en déduit alors que
$\dsum_nf_n(x)$ converge. Ce qui donne $\dsum f_n$ converge simplement sur $\R_+^*$, notons $S$ sa
somme.
Étudions la convergence normale. Pour tout $n\in \N,\, f_n\in \CC^1(\R_+^*)$ et on a
$$\forall x>0, \, f_n'(x)=nx^{\alpha-1}(\alpha-2nx^2)\ee^{-nx^2}.$$
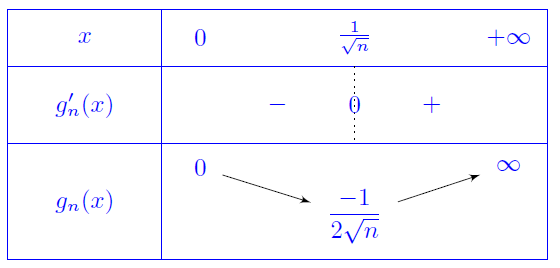
Ce qui donne le tableau de variation suivant:
on en déduit que
$\norme{f_n}_\infty=\sqrt{\alpha/2}n^{1-\alpha/2}\ee^{-\alpha/2}=\mathrm{O}(n^{1-\alpha/2})$.
Donc $\dsum f_n $ CN sur $\R_+^*$ pour $\alpha\in ]4,\infty[$.
Pour $\alpha\leq 4$ il n'y a pas de convergence normale sur $\R_+^*$, mais
$\dsum f_n$ CN sur tout intervalle de type $[a,\infty[$ avec $a>0$, puisque, pour
$n\geq \dfrac{\alpha}{2a^2}$, $\norme{f_n}_\infty^{[a,\infty[}= f_n(a)$ et $\dsum f_n(a)$ converge.
Étudions maintenant la convergence uniforme de $\dsum f_n$ pour $\alpha\in ]0,4]$. Pur cela, il faut
étudier $R_n(x)$.
Soit $x>0$, on pose $g(t)=tx^\alpha\ee^{-tx^2}$, un étude rapide de la fonction $g$, montre que $g$
est strictement décroissante sur $]1/x^2,\infty[$. Ainsi,
$$\forall n\in \N,\,n\geq \dfrac{1}{x^2},\, g(t)\leq g(n)\Longrightarrow \int_n^{n+1}g(t)\ud t\leq
nx^\alpha\ee^{-nx^2}.$$
En faisant la somme dans la relation précédente, pour $k\geq n+1$, on obtient,
$$\forall n\in \N, \, n\geq \dfrac{1}{x^2},\quad R_n(x)\geq \int_n^\infty g(t)\ud
t=(1+nx^2)x^{\alpha-4}\ee^{-nx^2}.$$
En particulier, pour $x=\dfrac{1}{\sqrt{n}}$, on trouve,
$R_n\left(\frac{1}{\sqrt{n}}\right)\geq 2\ee^{-1}n^{\frac{4-\alpha}{2}}$.
On en déduit alors que $(R_n)$ ne converge uniformément vers $0$. Donc $\dsum f_n$ ne converge pas
uniformément sur $\R_+^*$.
On définit $f_n(x)=\dfrac{1}{n^x}$ et $\zeta(x)=\dsum_{n\geq 1} f_n(x)$.
- Déterminer le domaine de définition de $\zeta$.
- Déterminer $\dsp\lim_{x\to \infty}\zeta (x)$. Puis trouver un équivalent de $\zeta$ au voisinage de $1^+$.
- Montrer que $\zeta \in \CC^\infty (]1,\infty[)$. Déterminer $\zeta^{(k)}$.
- Montrer que $\zeta $ est convexe.
-
- Pour $x=1$, on sait que $\dsum \dfrac 1 n $ diverge, donc $1\not \in D_\zeta$
- Pour $x\in ]-\infty,1[$ et pour tout $n\geq 1$, on a $$0\leq f_n(x) =\dfrac{1}{n^x} \geq \dfrac{1}{n} \Longrightarrow \dsum f_n(x) \text{ diverge}.$$
- Pour $x>1$, $\dsum\dfrac{1}{n^x}$ converge (série de Riemann)
-
- Au voisinage de $\infty$, $\dsum f_n$ converge uniformément, donc d'après le cours: $$\lim_{x\to \infty}\zeta(x)=\dsum_{n\geq 1}\lim_{x\to \infty} f_n(x)= 1$$ En effet, pour $n\geq 2,\,\dfrac{1}{n^x}\tendvers{x}{\infty}\,0$.
- Soit $x> 1$, la fonction $g(t)=\dfrac{1}{t^x}= \ee^{-x\ln (t)}$ est strictement décroissante sur $[1,\infty[$, ainsi, $$\forall n\geq 2,\quad \int_n^{n+1} g(t)\ud t \leq g(n)=f_n(x)\leq \int_{n-1}^ng(t)\ud t.$$ Comme $\dsp\int_1^\infty g(t)\ud $ converge, alors en faisant la somme dans la relation précédente, pour $n\geq 2$, on trouve : $$\int_2^\infty \dfrac{\ud t}{t^x} \leq \dsum_{n\geq 2} \dfrac{1}{n^x} \leq \int_1^\infty \dfrac{\ud t}{t^x}$$ On obtient finalement , $$ 1+\dfrac{1}{x-1}\dfrac{1}{2^{x-1}}\leq \zeta(x) \leq 1 + \dfrac{1}{x-1} $$ Ainsi, $$ \boxed{\zeta(x) \underset{x\to 1^+}{\sim}\dfrac{1}{x-1}}.$$ On peut montrer également que $$\zeta(x) \underset{x\to 1^+}{=}\dfrac{1}{x-1}+\gamma +\mathrm{o}(1).$$
- Pour tout $n\in \N^*$, $f_n\in \CC^\infty(]1,\infty[)$, et on a : $$\forall k\in \N,\quad \forall x> 1,\quad f_n^{(k)}(x)=(-1)^k\dfrac{\ln(n)^k}{n^x}.$$ Soit $a > 1$, pour tout $x \geq a$, on a : $$\abs{f_n^{(k)}(x)} \leq \dfrac{\ln(n)^k}{n^a} \Longrightarrow \norme{f_n^{(k)}}_\infty^{[a,\infty[}=\abs{f_n^{(k)}(a)}$$ or $\dsum \abs{f_n^{(k)}(a)}$ converge, donc $\dsum f_n^{(k)}$ converge normalement (donc uniformément) sur $[a,\infty[$.$\\$ $a$ étant arbitairement choisi dans $]1,\infty[$, alors d'après le cours, $$\zeta \in \CC^\infty(]1,\infty[),\text{ et pout tout } n\in \N^*,\forall x> 1\quad f^{(k)}(x)=\dsum_{n\geq 1} \dfrac{(-1)^k\ln(n)^k}{n^x}$$
- D'après la question précédente, pour tout $x> 1$, $$\zeta'(x)=\dsum_{n\geq 2} \dfrac{-\ln(n)}{n^x} < 0,\quad \zeta''(x) = \sum_{n\geq 2}\dfrac{\ln(n)^2}{n^2}> 0$$ Ainsi, $\zeta$ est strictement décroissante sur son domaine de définition, et $\zeta $ est convexe.
Recherche équivalent
- Quel est le domaine de définition de $S:x\longmapsto\dsp\sum_{n=1}^\infty\dfrac{1}{n^2x+n}$.
- Montrer que $S\in \CC^1(\R_+^*)$.
- Déterminer un équivalent de $S$ en $\infty$ puis en $0^+$.
$\mathbf{ 1.}\,$ Il faut d'abord que $n^2x+n$ ne s'annule pas, i.e. $x\not \in \left\{\frac{-1}{k},\,k\in \N^*\right\}$. Ensuite, il faut que $\dsum_{n=1}^\infty\dfrac{1}{n^2x+n}$ converge, soit $x\in \R\setminus \left\{\frac{-1}{k},\,k\in \N^*\right\}$, alors:
- Si $x\neq 0$ alors $\dfrac{1}{n^2x+n}\underset{n\infty}{\thicksim}\dfrac{1}{n^2x}$ et comme $\dsum_{n=1}^\infty\dfrac{1}{n^2x}$ converge, on en déduit que $\dsum_{n=1}^\infty\dfrac{1}{n^2x+n}$ converge.
- Si $x=0$ alors $\dsum_{n=1}^\infty\dfrac{1}{n}$ diverge donc $S$ n'est pas définie en $0$.
En conclusion $\boxed{\DD_S=\R^*\setminus \left\{\frac{-1}{k},\,k\in \N^*\right\}}$.
$\mathbf{2. }\,$ Pour $n\in \N^*$, notons $u_n(x)=\dfrac{1}{n^2x+n}$, on a
$u_n\in \CC^1(\DD_S)$ de plus $\dsum u_n$ converge simplement sur $\R_+^*$, donc pour montrer que
$S$ est de classe $\CC^1$ sur $\R_+^*$ il faut montrer que $\dsum u_n'$ converge uniformément
(ou localement uniformément) sur $\R^*$.
Soit $a>0$, on a $\forall x\in [a,\infty[,~~u_n'(x)=\dfrac{-n^2}{(n^2x+n)^2}$, donc
$$\forall n\in \N^*,\,\forall x\in [a,\infty[,~~\abs{u_n'(x)}\leq \dfrac{1}{n^2a}
\Longrightarrow \dsum_{n\geq 1}\norme{u_n'}_\infty^{[a,\infty[}< \infty.$$
La série $\dsum_{n\geq 1}u_n'$ est normalement localement (donc uniformément) sur $\R^*$, il en
résulte $\boxed{S\in \CC^1(\R_+^*)} $.
$\mathbf{3. }\,$ Au voisinage de $\infty$:
Pour tout $x>0$, on a
$$\begin{array}{lcl}
\forall n\in \N^*,~~n^2x\leq n^2x +n\leq n^2x+n^2&\Longrightarrow& \forall n\in \N^*,~~
\dfrac{1}{n^2(x+1)}\leq \dfrac{1}{n^2x+n}\leq \dfrac{1}{n^2x}\\
&\Longrightarrow &\dfrac{1}{x+1}\dsum_{n\geq 1}\dfrac{1}{n^2}\leq S(x)\leq \dfrac{1}{x}
\dsum_{n\geq 1}\dfrac{1}{n^2}.
\end{array}$$
On en déduit $\boxed{ S(x)\underset{x\rightarrow\infty}{\thicksim}\dfrac{\pi^2}{6x}}$.
Au voisinage de $0^+$:
Soit $x>0$, la fonction $g:t\longmapsto\dfrac{1}{xt^2+t}$ est de classe $\CC^1$ sur $\R_+^*$
strictement décroissante. Donc
$$\forall n\geq 2,~~\int_n^{n+1}g(t)\ud t\leq g(n)=u_n(x)\leq \int_{n-1}^ng(t)\ud t
\Longrightarrow \int_1^\infty g(t)\ud t\leq S(x)\leq \int_1^\infty g(t)\ud t+\dfrac{1}{x+1}.$$
Un calcul simple de $\dsp\int_1^\infty g$ (il faut remarquer qu'il s'agit d'une
intégrale convergente) donne $\dsp\int_1^\infty g(t)\ud t=\ln(x+1)-\ln(x)$, d'où,
$$\forall x\in ]0,1[,~~~~ 1-\dfrac{\ln(x+1)}{\ln(x)}\leq \dfrac{S(x)}{-\ln(x)}\leq
1-\dfrac{\ln(x+1)}{\ln(x)}-\dfrac{1}{(x+1)\ln(x)}\Longrightarrow \boxed{ S(x)\underset{x\rightarrow
0^+}{\thicksim}-\ln(x)}.$$
Existence et équivalent en $0$ de $S(x)=\dsum\limits_{n=1}^{\infty}\dfrac{\Arctan nx}{n^2}$.
Existence immédiate sur tout~$\R$ grâce à la convergence normale, dont on déduit la continuité.
On a donc $\lim\limits_{x\to 0} S(x)=0$.
On utilise le fait que, pour $x$ fixé, la fonction $t\mapsto\dfrac{\Arctan tx}{t^2}$ est décroissante.
En effet, la fonction $t\mapsto \dfrac{\Arctan t}{t^2}$ l'est :
On dérive : $f'(t)=\dfrac{t^2-2(1+t^2)t\Arctan t}{t^4(1+t^2)}$. Il faut montrer que le numérateur est
toujours négatif. Pour cela, on pose $g(t)=2(1+t^2)\Arctan t-t=h(t)-t.$ Or $h'(t)=2+2t\Arctan t\geq 2$
pour tout $t\geq 0$, ce qui montre que la dérivée de~$g$ est toujours positive, et on peut conclure,
avec $g(0)=0$, que $g$ est toujours positive, donc $f$ est décroissante.
On en déduit que
$$\displaystyle \dsp \int_n^{n+1}\dfrac{\Arctan tx}{t^2}\,\ud t \leq
\dfrac{\Arctan nx}{n^2} \leq \dsp \int_{n-1}^n \dfrac{\Arctan
tx}{t^2}\,\ud t$$
et donc, après sommation et changement de variable,
$$\displaystyle x \dsp \int_{2x}^{+\infty} \dfrac{\Arctan y}{y^2}\,\ud y
\leq \dsum_{k=2}^\infty \dfrac{\Arctan nx}{n^2} \leq x\dsp \int_x^{+\infty}
\dfrac{\Arctan y}{y^2}\,\ud y.$$
Or on a $\displaystyle
\dsp \int_x^{+\infty} \dfrac{\Arctan y}{y^2}\,\ud y \underset{x\to 0^+}{\sim} -\ln x,$
comme on peut le voir en montrant que la différence de ces deux termes admet une limite finie
(utiliser la relation de Chasles puis écrire $-\ln x=\dsp \int_x^1 \dfrac{\ud t}t$), ce qui montre que
$$S(x)=\dsum\limits_{n=1}^{\infty} \dfrac{\Arctan
nx}{n^2}\underset{x\to0^+}{\sim}-x\ln x.$$
Trouver un équivalent de $f(x)=\dsum_{n\geq 0}\dfrac{1}{\ch (nx)}$ quand $x$ tend vers $0^+$.
$f$ est bien définie sur $\R_+^*$ (c.f. exercice précédent).
Pour $x>0$, on définit $\fonct{\varphi}{\R_+}{\R}{t}{\frac{1}{\ch (xt)}}$. La fonction $\varphi$ est
continue strictement décroissante sur $\R_+$. Donc
$$\forall n\in \N,\quad f(n+1)\leq \int_n^{n+1}\varphi(u)\ud u\leq f(n)\Longrightarrow
-\varphi(0)+\dsum_{n\geq 0}\varphi (n)\leq \int_0^\infty \varphi (u)\ud u\leq \dsum_{n\geq
0}\varphi(n).$$
Notons que $\dsp\int_0^\infty \varphi (u)\ud u$ converge et $\dsum_{n\geq 0}\varphi(n)=f(x)<
\infty$.
On en déduit,
$$\forall x>0, \int_0^\infty\dfrac{\ud u}{\ch (xu)}\leq f(x)\leq \int_0^\infty\dfrac{\ud u}
{\ch (xu)}+1\Longrightarrow
\left[\dfrac{2\Arctan (\ee^{xu})}{x}\right]_0^\infty \leq f(x)
\leq \left[\dfrac{2\Arctan (\ee^{xu})}{x}\right]_0^\infty +1.$$
Ce qui donne $\boxed{ f(x)\underset{x\rightarrow 0^+}{\thicksim}\dfrac{\pi}{2x}}$.
- Déterminer le domaine de définition $\DD$ de la fonction $f$ définie par $f(x)=\dsum_{n\geq 1}\dfrac{\ee^{-x\sqrt{n}}}{\sqrt{n^3}}$.
- Étudier les propriétés de $f$ sur $\DD$ ainsi que la dérivabilité de $f$ en $0$.
- Déterminer une équivalent de $f$ en $\infty$.
-
Posons, pour $n\geq 1$, $\fonct{u_n}{\R}{\R}{x}{\dfrac{\ee^{-x\sqrt{n}}}{\sqrt{n^3}}}$.
Pour $x< 0$, on a $\dfrac{\ee^{-x\sqrt{n}}}{\sqrt{n^3}}\tendversN\infty$, donc $x\not\in \DD$.
Pour $x\geq 0$, on a $0\leq u_n(x)\leq \dfrac{1}{\sqrt{n^3}}$, et comme $\dsum \dfrac{1}{n^{3/2}}$ converge alors $\dsum u_n(x)$ converge donc $x\in \DD$.
On en déduit que $\DD=\R_+$. De plus, on a $\norme{u_n}_\infty^{\R_+}=\dfrac{1}{\sqrt{n^3}}$ donc $\dsum u_n$ converge normalement sur $\DD$. -
- $f$ est continue sur $\DD$ car $\dsum u_n$ converge normalement (donc uniformément) sur $\DD$ et pour tout $n\geq 1$ $u_n$ est continue sur $\DD$.
- Notons que la fonction $x>0\longmapsto \dfrac{f(x)-f(0)}{x}$ est strictement
décroissante sur $\R_+^*$ et continue donc elle admet une limite en $0$
(éventuellement $-\infty$).
Pour tout $n\geq 1$, on a $u_n\in \CC^1(\DD)$ et $u_n(x)'=\dfrac{-\ee^{-x\sqrt{n}}}{n}$. Soit $a>0$, on a $$\forall x\in [a,\infty[,\quad \abs{u_n'(x)}\leq \dfrac{\ee^{-a\sqrt{n}}}{n} \Longrightarrow\norme{u_n'}_\infty^{[a,\infty[}\leq \dfrac{\ee^{-a\sqrt{n}}}{n}\Longrightarrow \dsum_{n\geq 1}\norme{u_n'}_\infty^{[a,\infty[}< \infty.$$ Ceci prouve que $\dsum u_n'$ converge normalement (donc uniformément) sur $[a,\infty[$, d'où $\dsum u_n'$ converge uniformément localement sur $\R_+^*$. On en déduit que $f\in \CC^1(\R_+^*)$. - Pour $N\in \N$ et $x>0$, on pose
$g_N(x)=\dsum_{n=1}^N\dfrac{\ee^{-x\sqrt{n}}-1}{x\sqrt{n^3}}=
\dsum_{n=1}^N\dfrac{1}{n}\left(\dfrac{\ee^{-x\sqrt{n}}-1}{x\sqrt{n}}\right)$.
La fonction $\varphi(t)=\dfrac{\ee^{-t}-1}{t}$ est continue sur $\R^*$ et prolongeable par continué en $0$ en posant $\varphi(0)=-1$. On en déduit que $g_N$ est prolongeable par continuité en $0$ avec $$g_N(0)=\limiteX{x}{0^+}\dsum_{n=1}^N\dfrac{1}{n}\left(\dfrac{\ee^{-x\sqrt{n}}-1}{x\sqrt{n}}\right)=\dsum_{n=1}^N\limiteX{x}{0^+}\varphi(x\sqrt{n})\dfrac{1}{n}=-\dsum_{n=1}^N\dfrac{1}{n}$$ Soit $x>0$, on a $$\dfrac{f(x)-f(0)}{x}=\dsum_{n\geq 1}\dfrac{\ee^{-x\sqrt{n}}-1}{x\sqrt{n}}\dfrac{1}{n}\leq g_N(x)\Longrightarrow\limiteX{x}{0^+}\dfrac{f(x)-f(0)}{x}\leq \limiteX{x}{0^+}g_N(x)=-\dsum_{k=1}^N\dfrac{1}{k}$$ Ceci étant vrai pour tout $N\in \N^*$, on en déduit alors que $\dsp\limiteX{x}{0^+}\dfrac{f(x)-f(0)}{x}=-\infty$ puisque $\dsum\dfrac{1}{k}$ diverge. On conclut que $f$ n'est pas dérivable en $0$.
- La convergence de $\dsum u_n$ est uniforme sur $[1,\infty[$, de plus, pour tout $n\geq 1$, on a $u_n(x)\tendvers{x}{\infty}0$, on en déduit: $\limiteX{x}{\infty}f(x)=\dsum_{n\geq 1}\limiteX{x}{\infty}u_n(x)=0.$ Pour trouver un équivalent de $f$ en $\infty$, on écrit, $$\begin{array}{lcl} f(x)&=&\ee^{-x}+\dfrac{\ee^{-x\sqrt{2}}}{2}+\dfrac{\ee^{-x\sqrt{3}}}{3}+\cdots\\ &=&\ee^{-x}\left(1+\dfrac{\ee^{-x(\sqrt{2}-1)}}{2}+\dfrac{\ee^{-x(\sqrt{3}-1)}}{3}+\cdots\right)\\ &=&\ee^{-x}\left(1+\dsum_{k\geq 2}\dfrac{\ee^{-x(\sqrt{k}-1)}}{k}\right)=\ee^{-x}\left(1+h(x)\right) \end{array}$$ ensuite on montre que $h(x)\tendvers{x}{\infty}0$, ce qui donne $f(x)\underset{x\to \infty}{\thicksim}\ee^{-x}$.
- Déterminer le domaine de définition $\DD$ de la fonction $f$ définie par $f(x)=\dsum_{n\geq 2}\dfrac{n^{-x}}{\ln(n)}$.
- Montrer que $f$ est de classe $\CC^\infty$ sur $\DD$.% ainsi que la dérivabilité de $f$ en $0$.
- Déterminer une équivalent de $f$ en $\infty$.
-
Pour $x\leq 1$ et $n\geq 2$, on a $\dfrac{n^{-x}}{\ln(n)}\geq \dfrac{1}{n\ln(n)}$ et
$\dsum \dfrac{1}{n\ln(n)}$ diverge donc $x\not\in \DD$.
Pour $x>1$ on a $\dfrac{n^{-x}}{\ln(n)}=\underset{n\to \infty}{\mathrm{o}} \left(\dfrac{1}{n^{\frac{1+x}{2}}} \right)$ et $\dsum \dfrac{1}{n^{(1+x)/2}}$ converge donc $x\in \DD$.
On en déduit $\boxed{\DD=]1,\infty[}$. -
Posons, pour $n\geq 2$, $\fonct{f_n}{]1,\infty[}{\R}{x}{\dfrac{1}{n^x\ln(n)}}$, on a $f_n\in
\CC^\infty(]1,\infty[)$. De plus,
$$\forall p\in \N^*,\quad \forall x\in ]1,\infty[,\quad
f_n^{(p)}(x)=\dfrac{\ln(n)^{p-1}}{n^x}\Longrightarrow
\forall a>1,\quad \norme{f_n^{(p)}}_\infty^{[a,\infty[}\leq \dfrac{\ln(n)^{p-1}}{n^a}$$
Donc $$\dsum_{n\geq 2} \norme{f_n^{(p)}}_\infty^{[a,\infty[}< \infty.$$
Donc la série $\dsum f_n^{(p)}$ converge normalement sur tout intervalle de type $[a,\infty[$
pour tout $a>1$.
On en déduit que $\dsum f_n^{(p)}$ converge uniformément localement sur $]1,\infty[$.
Le résultat étant vérifié pour tout $p\in \N$, on en déduit alors que $f\in \CC^\infty(]1,\infty[)$. -
Pour tout $n\geq 2$, on a $f_n(x)=\dfrac{1}{n^x\ln(n)}\tendvers{x}{\infty}0$. Comme $\dsum f_n$
converge normalement sur $[a,\infty[$ ($a>1$), on en déduit alors que
$\dsp\limiteX{x}{\infty}f(x)=
\dsum_{n\geq 2}\limiteX{x}{\infty}f_n(x)=0$.
D'autre part, on a $$f(x)=\dfrac{1}{2^x\ln(2)}+\dfrac{1}{3^x\ln(3)}+\cdots +\dfrac{1}{n^x\ln(n)}+\cdots =\dfrac{1}{2^x\ln(2)}\left(1+\left(\frac{2}{3}\right)^x\frac{\ln(2)}{\ln(3)}+\cdots +\left(\frac{2}{n}\right)^x\frac{\ln(2)}{\ln(n)}+\cdots\right)$$ Ainsi, $\dsp\ln(2)2^xf(x)=1+\dsum_{n\geq 3}\left(\dfrac{2}{n}\right)^x\dfrac{\ln(2)}{\ln(n)}\tendvers{x}{\infty}1$. On en déduit, $\boxed{f(x)\underset{x\to\infty}{\thicksim}\dfrac{1}{2^x\ln(2)}}$.
Soit $a\in ]-1,1[$ et $S:[0,1[\longmapsto \R$ définie par $S(x)=\dsum_{n\geq 1}\dfrac{a^n}{1-x^n}$.
- Montrer que $S$ est continue sur son domaine de définition.
- Montrer que pour tout $a\in ]-1,1[$, $\dsum_{n\geq 1}\dfrac{a^n}{n}=-\ln(1-a)$.
- Trouver un équivalent de $S(x)$ quand $x$ tend vers $1$.
-
Soit $a\in ]-1,1[$, on définit pour $n\geq 1$, $\fonct{f_n}{[0,1[}{\R}{x}{\frac{a^n}{1-x^n}}$.
Il est clair que $f_n$ est continue sur $[0,1[$.
Soit $b\in ]0,1[$, on a $$\forall x\in [0,b],\quad \abs{f_n(x)}=\dfrac{\abs{a}^n}{1-x^n}\leq \dfrac{\abs{a}^n}{1-b} \Longrightarrow\norme{f_n}_\infty^{[0,b]}\leq \dfrac{\abs{a}^n}{1-b}\Longrightarrow \dsum_{n\geq 1} \norme{f_n}_\infty^{[0,b]} < \infty.$$ Donc la série $\dsum f_n$ converge normalement sur $[0,b]$ ce qui implique la convergence uniforme (et simple) sur $[0,b]$.
La série $\dsum f_n$ converge donc uniformément localement sur $[0,1[$ donc sa somme $S$ est continue sur $[0,1[$. - Soit $a\in ]-1,1[$, la série $\dsum (x\longmapsto x^n)$ converge normalement sur $[-\abs{a},\abs{a}]$ vers la fonction $x\longmapsto \dfrac{1}{1-x}$. On en déduit, $$\forall y\in [-\abs{a},\abs{a}],\quad -\ln(1-y)=\int_0^y\dfrac{\ud x}{1-x}=\dsum_{n\geq 1}\int_0^yx^n\ud x=\dsum_{n\geq 0}\dfrac{y^{n+1}}{n+1}=\dsum_{n\geq 1}\dfrac{y^n}{n}\Longrightarrow \dsum_{n\geq 1}\dfrac{a^n}{n}=-\ln(1-a).$$
-
Posons pour $n\geq 1,\,\,\fonct{g_n}{[0,1[}{\R}{x}{\dfrac{(1-x)a^n}{1-x^n}}$, i.e.
$g_n(x)=(a-x)f_n(x)$.
On a,
$$\forall x\in [0,1[,\quad \abs{g_n(x)}\leq \abs{a}^n\dfrac{1-x}{1-x^n}\leq
\abs{a}^n\Longrightarrow
\norme{g_n}_\infty^{[0,1[}\leq \abs{a}^n\Longrightarrow\dsum_{n\geq
1}\norme{g_n}_\infty^{[0,1[}< \infty.$$
Donc la série $\dsum g_n$ converge normalement (donc uniformément, simplement) sur $[0,1[$ et sa
somme est la
fonction $g(x)=(1-x)S(x)$.
D'autre part, pour tout $n\geq 1$, on a $$\forall x\in [0,1[,\quad g_n(x)=\dfrac{a^n}{1+x+\cdots +x^{n-1}}\tendvers{x}{1^{-}}\dfrac{a^n}{n},\text{ et } \dsum_{n\geq 1}\dfrac{a^n}{n}=-\ln(1-a).$$ On en déduit, alors $$\limiteX{x}{1^-}(1-x)S(x)=\dsum_{n\geq 1}\limiteX{x}{1^-}g_n(x)=\dsum_{n\geq 1}\dfrac{a^n}{n}=-\ln(1-a)\Longrightarrow \boxed{S(x)\underset{x\to 1^{-}}{\thicksim}\dfrac{-\ln(1-a)}{1-x}} .$$
On pose $f(x)=\dsum\limits_{n=1}^{\infty}\dfrac{1}{n(1+n^2x^2)}$. Montrer que $f$ est définie, continue et dérivable sur $\R^*$. Donner un équivalent de $f$ en $0$ et en $+\infty$.
Les fonctions sont décroissantes en $x$, il y a donc convergence normale sur $[a,+\infty[$
avec majoration des termes par leur valeur en $a$.
Pour l'équivalent en $\infty$, on va montrer que $f(x)\sim \dfrac{1}{x^2}\left(\dsum_{n\geq1}
\dfrac{1}{n^3}\right)$.
On commence par encadrer par exemple
$$\forall n\geq 1,\,\forall x>0,\quad\dfrac{1}{n^3x^2}\geq
\dfrac{1}{n(1+n^2x^2)} = \dfrac{1}{n^3x^2 (1+1/n^2x^2)}\geq
\dfrac{1}{x^2n^3}\left(\dfrac{1}{1+\dfrac{1}{x^2}}\right) .$$
On pose $\alpha = \dsum_{n=1}^{\infty} \dfrac{1}{n^3}$. On a alors après sommation :
$\dfrac{\alpha}{x^2} \left(\dfrac{1}{1+\dfrac{1}{x^2}}\right)
\leq f(x) \leq \dfrac{\alpha}{x^2}$,
ce qui montre que
$$\boxed{f(x)\sim \dfrac{1}{x^2}\left(\dsum_{n=1}^\infty \dfrac{1}{n^3}\right)}.$$
Pour l'équivalent en $0$, on compare avec une intégrale
$$\displaystyle \dsp \int_1^\infty \dfrac{\ud t}{t(1+t^2x^2)} =-\ln(x)+
\dfrac{1}{2}\ln(1+x^2)=-\ln x+\underset{x\to 0}{\mathrm{o}}(\ln x),$$
l'équivalent est $-\ln x$.
Pour $x>0$, on pose $f(x)=\dsum_{n=0}^\infty \dfrac{1}{n!(x+n)}$
- Montrer que $f$ est bien définie sur $\R_+^*$
- Déterminer $(a,b)\in \R^2$ vérifiant $f(x)=\dfrac{a}{x}+\dfrac{b}{x^2}+\underset{x\to \infty}{\mathrm{O}}\left(\frac{1}{x^2}\right)$.
- Pour $x> 0$ et $n\in \N$, on pose $f_n(x)=\dfrac{1}{n!\,(x+n)}$. Soit $x> 0$, on a (puisque $f_n(x)> 0$): $$ \dfrac{f_{n+1}(x)}{f_n(x)} = \dfrac{n!}{(n+1)!}\dfrac{x+n+1}{x+n}\tendversN\,0$$ On en déduit que $\dsum f_n(x)$ converge, i.e $\dsum f_n $ CS sur $\R_+^*$.
- Soit $x> 0$ , on a $$xf(x)=\dsum_{n=0}^\infty \dfrac{x}{n!(x+n)}=\dsum_{n=0}^\infty \dfrac{1}{n!(1+(n/x))}=\dsum_{n\geq 0}g_n(x)$$ avec $g_n(x)=\dfrac{1}{n!}\dfrac{1}{1+n/x}$, pour $x\geq 1$ (on fera tendre $x$ vers $\infty$), on a: $$\abs{g_n(x)}\leq \dfrac {1}{(n+1)!}\Longrightarrow \norme{g_n}_\infty ^{[1,\infty[}\leq \dfrac{1}{(n+1)!}$$ donc $\dsum g_n $ CN sur $[1,\infty[$, ce qui implique la convergence uniforme, d'autre part, on a : $$g_n(x)=\dfrac{1}{n!}\dfrac{1}{1+n/x}\tendvers{x}{\infty} \dfrac{1}{n!}$$ donc, d'après le cours ($\dsp \lim_{x\to \infty}\dsum g_n(x) =\dsum \lim_{x\to \infty}g_n(x)$) $$ xf(x)=\dsum_{n\geq 0 }g_n(x) \tendvers{x}{\infty} \dsum_{n\geq 0}\dfrac{1}{n!}=\ee $$ Puis, on écrit $$xf(x)-e =\dsum_{n\geq 0} \dfrac{x}{n!\,(x+n)}-\dsum_{n\geq 0} \dfrac{1}{n!} = \dsum_{n\geq 1} \dfrac{1}{n!}\dfrac{-n}{x+n}$$ ce qui donne $$x^2f(x)-\ee x = \dsum_{n\geq 1} \dfrac{1}{n!}\dfrac{-nx}{x+n}=-\dsum_{n\geq 1} \dfrac{1}{n!}\dfrac{n}{1+(n/x)}$$ En utilisant la démarche précédente, on montre que $$\lim_{x\to \infty}\left(x^2f(x)-\ee x\right) =-\dsum_{n\geq 1} \left( \lim_{x\to \infty} \dfrac{1}{n!}\dfrac{n}{1+(n/x)}\right)=-\ee .$$ Ainsi, $$\textcolor{blue}{\boxed{ f(x) = \dfrac{\ee }{x}+\dfrac{-\ee }{x^2}+\underset{x\to \infty}{\mathrm{O}}\left(\frac{1}{x^2}\right)}} $$
ApproximationPolynomial
Pour $n\in \N$, on pose $P_n:[-1,1]\longmapsto\R$ définie par $P_n(x)=\dsp\int_0^x(1-t^2)^n\ud t$.
On définit également $Q_n(x)=\dfrac{1}{P_n(1)}\dsp\int_0^xP_n(u)\ud u$.
Montrer que la suite $(Q_n)_n$ converge uniformément sur $[-1,1]$ vers la fonction valeur absolue.
Le polynôme $P_n$ ($n\in \N$) est un polynôme impaire de degré $2n+1$ ce qui donne $Q_n$ est un
polynôme paire de degré $2n+2$.
Notons $f(x)=\abs{x}$, comme $f$ et $Q_n$ sont des fonctions paires il suffit alors d'étudier
$Q_n-f$ sur $[0,1]$.
Pour $x\in [0,1]$, on va écrire :
$$x=\int_0^x\ud u=\dfrac{1}{P_n(1)}\left(\int_0^1(1-t^2)^n\ud t\right)\int_0^x\ud
u=\dfrac{1}{P_n(1)}\int_0^x \left(\int_0^1(1-t^2)^n\ud t\right)\ud u.$$
Ce qui donne
$$ \begin{array}{lcl}
\dsp Q_n(x)-x&=&\dsp \dfrac{1}{P_n(1)}\left( \int_0^x \left(\int_0^u(1-t^2)^n\ud t \right)\ud u -
\int_0^x \left(\int_0^1(1-t^2)^n\ud t\right)\ud u\right)\\
&&\\
&=& \dsp \dfrac{1}{P_n(1)}\left( \int_0^x \left(\int_u^1(1-t^2)^n\ud t \right)\ud u \right)\leq \dsp
\dfrac{1}{P_n(1)}\left( \int_0^1 \left(\int_u^1(1-t^2)^n\ud t \right)\ud u \right)\\
&&\\
&\underset{IPP}{=}&\dsp \dfrac{1}{P_n(1)}\left( \left[ u\int_u^1(1-t^2)\ud t\right]_0^1+\int_0^x
u(1-u^2)^n\ud u \right)\\
&&\\
&\leq&\dsp\dfrac{1}{2(n+1)P_n(1)}.
\end{array}
$$
Regardons maintenant $P_n(1)$
$$P_n(1)=\int_0^1(1-t^2)^n\ud t\underset{t=\cos(u)}{=}\int_0^{\frac{\pi}{2}}\sin(u)^{2n}\sin(u)\ud
u=W_{2n+1}\underset{n\rightarrow\infty}{\thicksim}\sqrt{\dfrac{\pi}{4n}}\Longrightarrow
\boxed{2(n+1)P_n(1)\tendversN\infty}.$$
On en déduit alors que $\dfrac{1}{2(n+1)P_n(1)}\tendversN\,0$, d'où
$$\boxed{ \norme{Q_n-f}_\infty\leq \dfrac{1}{2(n+1)P_n(1)}\tendversN\,0}.$$
Ce qui montre la convergence uniforme de la suite $(Q_n)$ vers la fonction valeur absolu.
On définit la suite $(P_n)_{n\in \N}$ de polynômes par $P_0=1$ et $P_{n+1}=P_n+\dfrac12(X-P_n^2)$.
- Montrer que : $\forall x\in\R_+^*$, $\forall n\in\N$, $P_{n+1}(x)-\sqrt{x} = \big(P_n(x)-\sqrt{x}\big)\big(1-\dfrac12{P_n(x)+\sqrt{x}}\big)$.
- Exprimer de même $P_{n+1}(x)+\sqrt{x}$ en fonction de $P_{n}(x)+\sqrt{x}$.
- Montrer que pour tout $x\in [0,1]$ et tout $n\in\N$, $\sqrt{x}\leq P_{n+1}(x)\leq P_n(x)\leq 1$.
- Montrer que $(P_n)_n$ converge simplement sur $[0,1]$ vers $\fonct{f}{[0,1]}{\R}{x}{\sqrt{x}.}$
- Donner le sens de variation de $x\mapsto P_n(x)-\sqrt{x}$ et celui de $x\mapsto P_n(x)+\sqrt{x}$ sur~$[0,1]$.
- Montrer que $(P_n)$ converge uniformément vers~$f$.
- On développe le second membre de l'égalité et on trouve le premier.
- De même, \begin{equation*} P_{n+1}+\sqrt{x}=\left(P_n+\sqrt{x}\right)\left(1-\dfrac{P_n-\sqrt{x}}{2}\right). \end{equation*}
- Pour $n=0$ on a bien sûr $\sqrt{x}\leq P_n(x)\leq 1$ sur $[0,1]$. On effectue ensuite une récurrence : on suppose $\sqrt{x}\leq P_n(x)\leq 1$. On obtient alors \begin{equation*} P_{n+1}(x)=P_n(x)+\dfrac{1}{2}\underbrace{\left(x-P_n^2(x)\right)}_{\leq 0} \leq P_n(x)\leq 1. \end{equation*} De plus, on a $\dfrac{P_n(x)+\sqrt{x}}{2}\leq 1$, donc \begin{equation*} P_{n+1}(x)-\sqrt{x} = \left(P_n(x)-\sqrt{x}\right) \left(1-\dfrac{P_n(x)+\sqrt{x}}{2}\right) \geq 0. \end{equation*} Ainsi, on a par récurrence la double inégalité voulue.
- Pour $x$ fixé, la suite $(P_n(x))_{n\in\N}$ est décroissante et minorée par~$\sqrt{x}$, elle converge donc ; notons $f(x)$ sa limite. En injectant dans la relation de définition de $P_{n+1}$, on obtient \begin{equation*} f(x)=f(x)+\dfrac12\left(x-f^2(x)\right), \end{equation*} donc $f^2(x)=x$, or les $P_n$ sont positifs donc $f(x)$ aussi. On a donc convergence simple vers~$x\mapsto\sqrt{x}$.
- Une récurrence montre que la première est décroissante et la seconde croissante (faire la récurrence sur les deux propriétés et montrer que, en notant $\psi_n(x)=P_n(x)-\sqrt{x}$ et $\phi_n(x)= P_n(x)+\sqrt{x}$, on a $\psi_{n+1}=\left(1+\dfrac12\phi_n\right)\,\psi_n$ et $\phi_{n+1}=\left(1-\dfrac12\phi_n\right)\,\phi_n$).
- Par décroissance de $\psi_n$, on a $0\leq P_n(x)-\sqrt{x}\leq P_n(0)$. or $P_n(0)\underset{n\to\infty}{\longrightarrow} 0$, ce qui montre la convergence uniforme.
Pour tout $f\in \CC([0,1],\C)$, on associe la suite de polynôme $(B_n(f))$ définie par $$B_n(f)(x)=\sum_{k=0}^n{n \choose k}f\left(\frac{k}{n}\right)x^k(1-x)^{n-k}.$$
- Déterminer $B_n(f)$ pour : $f(x)=1$, $f(x)=x$ et $f(x)=x^2$.
- Calculer $g_n(x)=\dsum_{k=0}^n{n \choose k}\left(\frac{k}{n}-x\right)^2x^k(1-x)^{n-k}.$
- Montrer que $$\forall x\in [0,1],\quad f(x)-B_n(f)(x)=\dsum_{k=0}^n{n \choose k}\left(f(x)-f\left(\frac{k}{n}\right)\right)x^k(1-x)^{n-k}.$$
- Soit $\varepsilon>0$, comme $f$ est uniformément continue alors: $$\exists \alpha>0,\,\forall u,v\in [0,1],\quad \abs{u-v}\leq \alpha\Longrightarrow \abs{f(u)-f(v)}\leq \varepsilon.$$ En décomposant la somme trouvé dans la question précédente suivant la partition $\inter{0,n}=J_n\cup I_n$, avec $I_n=\{k\in \inter{0,n},\,\abs{k/n-x}\leq \alpha\}$ et $J_n=\inter{0,n}\setminus I_n$. Montrer que $(B_n(f))_n$ converge uniformément sur $[0,1]$.
-
- Dans ce cas $f(x)=1$ ce qui donne $$B_n(f)(x)=\sum_{k=0}^n{n \choose k}1x^k(1-x)^{n-k}= \left( x+ (1-\right)^n=1.$$
- On suppose que $f(x)=x$ alors $$\begin{array}{lcl} B_n(f)(x)&=&\dsp\sum_{k=0}^n{n \choose k}\dfrac{k}{n} x^k(1-x)^{n-k}=\sum_{k=1}^n{n \choose k}\dfrac{k}{n} x^k(1-x)^{n-k}\\ &&\\ &=&\dsp\sum_{k=0}^n\dfrac{(n-1)!}{(k-1)!((n-1)-(k-1))!} x^k(1-x)^{n-k}=\sum_{k=1}^n{n-1 \choose k-1}x^k(1-x)^{n-k}\\ &&\\ &=&\dsp\sum_{k=0}^{n-1}{n-1 \choose k} x^{k+1}(1-x)^{n-1-k}=x\sum_{k=0}^{n-1}{n-1 \choose k} x^{k}(1-x)^{n-1-k}\\ &&\\ &=&x \end{array} $$
- Pour $f(x)=x^2$ je vous laisse le soin de vérifier $B_n(f)(x)=x^2+\dfrac{x(1-x)}{n}$.
- Soit $n\in \N^*$, on a pour tout $x\in [0,1]$, $$\begin{array}{lcl} g_n(x)&=&\dsum_{k=0}^n{n \choose k}\left(\frac{k^2}{n^2}-2x\dfrac{k}{n}+x^2\right)^2x^k(1-x)^{n-k}\\ &&\\ &=&\dsp \dsum_{k=0}^n{n \choose k}\dfrac{k^2}{n^2} x^k(1-x)^{n-k}-2x \dsum_{k=0}^n{n \choose k}\dfrac{k}{n} x^k(1-x)^{n-k}+x^2 \dsum_{k=0}^n{n \choose k}x^k(1-x)^{n-k}.\\ &&\\ &=&x^2+\dfrac{x(1-x)}{n}-2x^2+x^2=\dfrac{x(1-x)}{n}. \end{array}$$
- Il suffit décrire $f(x)= f(x) \dsum_{k=0}^n{n \choose k} x^k(1-x)^{n-k}$.
- Soit $x\in [0,1]$, on écrit $f(x)-B_n(f)(x)=a_n+b_n$ avec $a_n=\dsum_{k\in I_n}{n \choose k}\left(f(x)-f\left(\frac{k}{n}\right)\right) x^k(1-x)^{n-k}$ et $b_n=\dsum_{k\in J_n}{n \choose k}\left(f(x)-f\left(\frac{k}{n}\right)\right) x^k(1-x)^{n-k}$. On a alors, $$\abs{a_n}\leq \dsum_{k\in I_n}{n \choose k}\abs{f(x)-f\left(\frac{k}{n}\right)} x^k(1-x)^{n-k}\leq \varepsilon\dsum_{k\in I_n}{n \choose k} x^k(1-x)^{n-k}\leq \varepsilon.$$ D'autre part si $k\in J_n$ alors $1< \dfrac{\left(\frac{k}{n}-x\right)^2}{\alpha^2}$, ce qui donne $$\abs{b_n}\leq \dsum_{k\in J_n}{n \choose k}\abs{f(x)-f\left(\frac{k}{n}\right)} x^k(1-x)^{n-k}\leq \dfrac{2\norme{f}_\infty}{\alpha^2} \dsum_{k\in J_n}{n \choose k}\left(x-\frac{k}{n}\right)^2 x^k(1-x)^{n-k}\leq \dfrac{2\norme{f}_\infty}{\alpha^2} g_n(x)\leq \dfrac{\norme{f}_\infty}{2\alpha^2n}.$$ On en déduit, $$\norme{f-B_n(f)}_\infty\leq \varepsilon+\dfrac{\norme{f}_\infty}{2\alpha^2 n}.$$ Ce qui montre la convergence uniforme de $B_n(f)$ vers $f$.