Fonctions de plusieurs variables
Dérivées partielles
Soit $f:\R^2\to \R$ définie par $f((x,y))=\left\{\begin{array}{lcl} \dfrac{x^4+y^4}{x^2+y^2}&\text{ si }& (x,y)\neq (0,0)\\ 0&\text{ si }& (x,y)=(0,0). \end{array} \right.$. Étudier la continuité de $f$ en $(0,0)$. $f$ est-t-elle de classe $\CC^1$ sur $\R^2$?.
La fonction $f$ est de classe $\CC^\infty$ sur
$\R^2\setminus\{(0,0)\}$. Il faut alors étudier $f$ en $(0,0)$.
On munit $\R^2$ de la norme 2 ($\norme{(x,y)}=\sqrt{x^2+y^2}$), soit $X=(x,y)\neq (0,0)$, on a
$$\abs{f(X)-f(0,0)}=\dfrac{x^4+y^4}{\norme{X}^2}\leq
\dfrac{2\norme{X}^4}{\norme{X}^2}=2\norme{X}^2\tendvers{X}{(0,0)}\,0.$$
Ceci prouve que $f$ est continue en $(0,0)$.
Soit $h\in \R^*$, on a
$$\dfrac{f(h,0)-f(0,0)}{h}=\dfrac{\frac{h^4}{h^2}-0}{h}=h\tendvers{h}{0}0$$
ceci montre que $f$ admet une dérivée partielle par rapport à $x$ en $(0,0)$. Calculons $\dfrac{\partial
f}{\partial x}(x,y)$ pour $(x,y)\neq 0$,
$$\forall (x,y)\neq (0,0),\,\,\dfrac{\partial f}{\partial
x}(x,y)=\dfrac{4x^3(x^2+y^2)-2x(x^4+y^4)}{(x^2+y^2)^2} = \dfrac{2x^5 +4x^3y^2-2xy^4}{(x^2+y^2)^2},$$
et en particulier,
$$\forall x\neq 0,\quad \dfrac{\partial f}{\partial x}(x,0)=\dfrac{2x^5}{x^4}=x\tendvers{x}{0}\,0$$
donc $\dfrac{\partial f}{\partial x}$ est continue en $(0,0)$.
Par symétrie (vu que $f(x,y)=f(y,x)$), on en déduit que $\dfrac{\partial f}{\partial y}$ est continue en
$(0,0)$.
Conclusion $f$ est de classe $\CC^1$ sur $\R^2$.
Calculer les dérivées partielles d'ordre 2 des fonctions suivantes~: $$ \mathbf{a)\,}f(x,y) = x^2 (x + y),\quad \mathbf{b)\,}h(x,y) = \cos (xy),\quad \mathbf{c)\,} g(x,y)=\ln(1+x^2y^2)y$$
- $f$ est de classe $\CC^\infty$ sur $\R^2$, et on a $$ \dfrac{\partial f}{\partial x}(x,y)=3x^2+2xy,\, \,\dfrac{\partial f}{\partial y}(x,y)=x^2.$$ et $$ \dfrac{\partial^2f}{\partial x^2}(x,y)=6x+2y,\,\,\dfrac{\partial^2f}{\partial y^2}(x,y)=0,\, \,\dfrac{\partial^2f}{\partial y\partial x}(x,y)=2x =\dfrac{\partial^2f}{\partial x\partial y}(x,y).$$
- $h$ est de classe $\CC^\infty$ sur $\R^2$, $$ \dfrac{\partial h}{\partial x}(x,y)=-y\sin(xy),\, \,\dfrac{\partial h}{\partial y}(x,y)=-x\sin(xy).$$ et $$ \dfrac{\partial^2h}{\partial x^2}(x,y)=-y^2\cos(xy),\,\,\dfrac{\partial^2h}{\partial y^2}(x,y)=-x^2\cos(xy),\, \,\dfrac{\partial^2h}{\partial y\partial x}(x,y)=-xy\cos(xy)=\dfrac{\partial^2h}{\partial x\partial y}(x,y).$$
- $g$ est de classe $\CC^\infty$ sur $\R^2$ (En effet, $1+x^2y^2>0$), $$ \dfrac{\partial g}{\partial x}(x,y)=\dfrac{2xy^3}{1+x^2y^2},\, \,\dfrac{\partial g}{\partial y}(x,y)=\dfrac{2x^2y^2}{1+x^2y^2}.$$ et $$ \dfrac{\partial^2g}{\partial x^2 }(x,y)=\dfrac{-2x^2y^5+2y^3}{(1+x^2y^2)^2}),\,\,\dfrac{\partial^2g}{\partial y^2 }(x,y)= \dfrac{4yx^2}{(1+x^2y^2)^2},\, \,\dfrac{\partial^2g}{\partial y\partial x}(x,y)=\dfrac{6xy^2+2x^3y^4}{(1+x^2y^2)^2}=\dfrac{\partial^2g}{\partial x\partial y}(x,y).$$
Soit $f$ et $\varphi :\mathbb{R} \to \mathbb{R}$ deux applications de classe $\CC^2 $ et $F:\mathbb{R}^2 \to \mathbb{R}$ définie par $F(x,y) = f(x + \varphi (y))$
- Justifier que $F$ est de classe $\CC^2 $.
- Vérifier~l'égalité~: $\dfrac{{\partial ^2 F}}{{\partial x^2 }}\dfrac{{\partial F}}{{\partial y}} - \dfrac{{\partial ^2 F}}{{\partial x\partial y}}\dfrac{{\partial F}}{{\partial x}} = 0$.
Il est claire que $F$ est de classe $\CC^1$ sur $\R^2$ comme la somme et la composée des fonctions de
classes $\CC^1$.
Soit $(x,y)\in \R^2$, on a
$$\dfrac{\partial F}{\partial x}(x,y)=f'(x+\varphi(y)),\quad \dfrac{\partial F}{\partial
y}(x,y)=f'(x+\varphi(y))\varphi'(y).$$
Les deux dérivées partielles de $F$ sont également de classe $\CC^1$ (puisque $f,\varphi\in \CC^2$, donc
$f',\varphi'\in \CC^1(\R)$, et on a:
$$\begin{array}{lcl}
\dfrac{\partial^2 F}{\partial x^2}(x,y)&=&\dfrac{\partial }{\partial
x}(f'(x+\varphi(y)))=f''(x+\varphi(y))\\
\dfrac{\partial^2 F}{\partial y\partial x}(x,y)&=&\dfrac{\partial }{\partial
y}(f'(x+\varphi(y)))=f''(x+\varphi(y))\varphi'(y)\\
\dfrac{\partial^2 F}{\partial x\partial y}(x,y)&=&\dfrac{\partial }{\partial
x}(f'(x+\varphi(y))\varphi'(y))=f''(x+\varphi(y))\varphi'(y)\\
\dfrac{\partial^2 F}{\partial y^2}(x,y)&=&\dfrac{\partial }{\partial
y}(f'(x+\varphi(y))\varphi'(y))=f''(x+\varphi(y))\varphi'(y)^2+f'(x+\varphi(y))\varphi''(y)
\end{array}$$
Les quartes fonctions ci-dessus sont continues sur $\R^2$, on en déduit alors que $F\in
\CC^2(\R^2,\R)$.
Soit $(x,y)\in \R^2$, on a
$$ \begin{array}{lcl}
\dfrac{{\partial ^2 F}}{{\partial x^2 }}\dfrac{{\partial F}}{{\partial y}} - \dfrac{{\partial ^2
F}}{{\partial x\partial y}}\dfrac{{\partial F}}{{\partial x}}
&=&f''(x+\varphi(y))f'(x+\varphi(y))\varphi'(y)-f''(x+\varphi(y))\varphi'(y)f'(x+\varphi(y))\\
&=&0
\end{array}$$
Soit $\fonct{f}{\R^2}{\R}{(x,y)}{\Max (\abs{x},\abs{y})}$. Déterminer le plus grand ouvert de $\R^2$ sur le quel $f$ est de classe $\CC^1$.
Soit $\Delta_1\,:~~y=x$ et $\Delta_2\,:~~y=-x$. Notons $\Omega =\R^2\setminus (\Delta_1\cup \Delta_2)$.
$f$ est de classe $\CC^1$ sur $\Omega$ puisque la restriction de $f$ à $\Omega$ est:
$$(x,y)\longmapsto x\text{ ou } -x \text{ ou } y \text{ ou } -y.$$
Soit $x_0\in \R_+^*$, on a $f(x_0,x_0)=x_0$ et $f(x,x_0)=x$ pour $x>x_0$, et $f(x,x_0)=x_0$ pour $x\leq
x_0$. Ce qui donne:
$$\limiteX{x}{x_0^+}\dfrac{f(x,x_0)-f(x_0,x_0)}{x-x_0}=1,~~~~\limiteX{x}{x_0^-}\dfrac{f(x,x_0)-f(x_0,x_0)}{x-x_0}=0.$$
Donc $f$ n'admet pas de dérivée partielle par rapport à $x$ en $(x_0,x_0)$ donc $f$ n'est pas de classe
$\CC^1$ en $(x_0,x_0)$.
Le même raisonnement pour les autres cas montre que $f$ n'est pas de classe $\CC^1$ aux points de
$(\Delta_1\cup\Delta_2)$.
On en déduit que le plus grand ouvert de $\R^2$, sur le quel $f$ est de classe $\CC^1$ est $\Omega$.
Soit $f:\R^2\longmapsto \R$, définie par : $\dsp f(x,y)=\left\{\begin{array}{lcl} \dfrac{xy(x^2-y^2)}{x^2+y^2}&\text{ si }& (x,y)\neq (0,0)\\ &&\\ 0&\text{ si }&(x,y)=(0,0). \end{array} \right.$. Déterminer la classe de $f$ sur $\R^2$.
D'après les théorèmes du cours, $f$ est de classe $\CC^\infty$ sur $\R^2\setminus \{(0,0)\}$. De plus, on
a
$$\forall (x,y)\neq (0,0),~~\dfrac{\partial
f}{\partial\,x}(x,y)=\dfrac{y(x^4-y^4+4x^2y^2)}{(x^2+y^2)^2},\text{ et }\dfrac{\partial
f}{\partial\,y}(x,y)=-\dfrac{\partial f}{\partial\,x}(x,y).$$
Il faut étudier la continuité de $f$ en $(0,0)$. On a pour tout $(x,y)\neq (0,0)$,
$$\abs{f(x,y)}\leq \abs{xy}\abs{\dfrac{x^2-y^2}{x^2+y^2}}\leq \abs{xy}\tendvers{(x,y)}{(0,0)}0=f(0,0).$$
Ce qui montre que $f$ est continue en $(0,0)$.
D'autre part, comme $f(x,0)=0=f(0,y)$, on en déduit que $\dfrac{\partial
f}{\partial\,x}(0,0)=\dfrac{\partial f}{\partial\,y}(0,0)=0$. Il faut maintenant voir si les dérivées
partielles de $f$ sont continues en $(0,0)$
$$
\forall (x,y)\neq (0,0),~~\abs{\dfrac{\partial f}{\partial\,x}(x,y)}\leq
\abs{y}\left(\dfrac{\abs{x^2-y^2)}}{x^2+y^2}+\dfrac{4x^2y^2}{(x^2+y^2)^2}\right)\leq
2\abs{y}\tendvers{(x,y)}{(0,0)}0=\dfrac{\partial f}{\partial\,x}(0,0).$$
Ceci prouve la continuité des dérivées partielles de $f$ en $(0,0)$, donc $f$ est de classe $\CC^1$ sur
$\R^2$.
On regarde maintenant les dérivées d'ordre 2,
$$
\dfrac{\dfrac{\partial f}{\partial\,x}(0,y)-\dfrac{\partial
f}{\partial\,x}(0,0)}{y}=\dfrac{-y}{y}\tendvers{y}{0}-1,\quad\quad\dfrac{\dfrac{\partial
f}{\partial\,y}(x,0)-\dfrac{\partial f}{\partial\,y}(0,0)}{x}=\dfrac{x}{x}\tendvers{y}{0}1.$$
Donc les dérivées partielles seconde
$\dfrac{\partial^2 f}{\partial\,x\partial\,y}(0,0),\,\dfrac{\partial^2 f}{\partial\,y\partial\,x}(0,0)$
existent et valent
respectivement $-1$ et $1$, en particulier
$$\dsp\dfrac{\partial^2 f}{\partial\,x\partial\,y}(0,0)\neq \dfrac{\partial^2
f}{\partial\,y\partial\,x}(0,0)\Longrightarrow f \text{ n'est pas de classe }\CC^2 \text{ en }
(0,0).$$
Soit $f\in \CC^\infty(\R,\R)$. Pour $x\neq y$, on pose $F(x,y)=\dfrac{f(x)-f(y)}{x-y}$.
- Montrer que $F$ se prolonge par continuité sur $\R^2$ en une application $\overline{F}$.
- Montrer que $\overline{F}$ est de classe $\CC^\infty$ sur $\R^2$ puis calculer $ \dsp\dfrac{\partial^{n+p}\overline{F}}{\partial^n x\,\partial^p y}(x,x).$
Comme $f$ est de classe $\CC^\infty$ sur $\R$, on en déduit que $F$ est de classe $\CC^\infty$ sur
$\R^2\setminus\{(x,x),\,x\in \R\}$.
Soit $y\in \R$, puisque $f$ est dérivable en $y$, alors
$\dsp\limiteX{x}{y}F(x,y)=\limiteX{x}{y}\dfrac{f(x)-f(y)}{x-y}=f'(y)$.
On en déduit que $F$ est prolongeable sur $\R^2$ en $\overline{F}$, avec: $\dsp\forall (x,y)\in
\R^2,~~~~\overline{F}(x,y)=\left\{\begin{array}{lcl}
F(x,y)&\text{ si } &x\neq y\\
f'(y)&\text{ si }& x=y.
\end{array}
\right.$.
Puis en utilisant la continuité de $f'$, on a:
$$\forall (x,y)\in \R^2,~~\overline{F}(x,y)=\int_0^1f'(y+t(x-y))\ud t.$$
Notons $\fonct{\varphi}{\R^2\times [0,1]}{\R}{((x,y),t)}{f'(y+t(x-y))}$, $\varphi$ est continue sur son
domaine de définition comme composition des fonctions continues.
Le théorème de continuité d'une intégrale sur un segment (ici $[0,1]$) dépendant d'un paramètre (ici
$(x,y)$) assure la continuité de $\overline{F}=\dsp\int_0^1\varphi(\cdot,t)\ud t$.
La fonction $\varphi$ est de classe $\CC^\infty$ sur son domaine de définition, donc d'après le théorème
de dérivation sous le signe intégrale sur un segment nous assure que $\overline{F}$ l'est également sur
$\R^2$. On a pour tout $(n,p)\in \N^2$,
$$\forall (x,y)\in \R^2,~~\dfrac{\partial^{n+p}
\overline{F}}{\partial^n\,x\partial^p\,y}(x,y)=\int_0^1\dfrac{\partial^{n+p}
\varphi}{\partial\,x^n\partial\,y^p}((x,y),t)\ud t=\int_0^1f^{(n+p+1)}(y+t(x-y))t^n(1-t)^p\ud t.$$
En particulier,
$$\forall x\in \R,~~\dfrac{\partial^{n+p}
\overline{F}}{\partial^n\,x\partial^p\,y}(x,x)=\int_0^nf^{(n+p+1)}(x)t^n(1-t)^p=f^{(n+p+1)}(x)I_{n,p}.$$
Avec, $I_{n,p}=\dsp\int_0^1t^n(1-t)^p\ud t$, en faisant $n$ intégration par parties, on trouve:
$$I_{n,p}=\dfrac{n!}{(p+1)(p+2)\cdots (p+n)}\int_0^n(1-t)^{n+p}\ud
t=\dfrac{n!p!}{(n+p)!}\dfrac{1}{n+p+1}.$$
Ce qui donne finalement,
$$\boxed{\forall x\in \R,\,\dfrac{\partial^{n+p}
\overline{F}}{\partial\,x^n\partial\,y^p}(x,x)=\dfrac{n!p!}{(n+p)!}\dfrac{f^{(n+p+1)}(x)}{n+p+1}}.$$
Donner le domaine de définition $\DD\subset \R^2$ de la fonction:
$$f(x,y)=\int_0^\pi \ln\left(x+y\cos(t)\right)\ud t.$$
Calculer la dérivée partielle de $f$ par rapport à $x$ lorsqu'elle existe.
En déduire l'expression de $f(x,y)$ lorsque $\abs{y}\leq x$.
Si $x>\abs{y}$, alors pour tout $t\in [0,\pi]$, on a $x+y\cos(t)>0$. Donc $f$ est bien définie sur
$\{(x,y)\in \R^2,\,x>\abs{y}\}$.
D'autre part, $\ln(1-\cos(t))\underset{t\rightarrow 0}{\sim}2\ln(t)$, comme $\dsp\int_0^\pi\ln(t)\ud t$
converge alors $\dsp\int_0^\pi\ln(1-\cos(t))\ud t$ converge également.
Le changement de variable $u=\pi-t$ montrer également que $\dsp\int_0^\pi\ln(1+\cos(t))\ud t$ converge
aussi.
Ainsi, pour tout $x>0$, $f(x,x)$ et $f(x,-x)$ sont bien définies. De plus, on a:
$$ \forall x>0,~~f(x,x)=f(x,-x)=\pi\ln(x)+\int_0^\pi\ln(1+\cos(t))\ud t.$$
On en déduit que $\boxed{\DD=\left\{(x,y)\in \R_+^*\times \R,~~x\geq \abs{y}\right\}}.$
Pour tout $y\in \R$, la fonction $(x,t)\longmapsto \ln(x+y\cos(t))$ est de classe $\CC^1$ sur
$]\abs{y},\infty[\times [0,\pi]$. Le théorème de dérivation sous le signe intégrale, nous donne que $f$
est dérivable par rapport à $x$ et,
$$\forall x>\abs{y},~~\dfrac{\partial f}{\partial x}(x,y)=\int_0^\pi\dfrac{\ud t}{x+y\cos(t)}.$$
En faisant le changement de variable $u=\tan (t/2)$, on trouve:
$$\forall x>\abs{y},~~\dfrac{\partial f}{\partial x}(x,y)=2\int_0^\infty\dfrac{\ud
u}{x(1+u^2)+y(1-u^2)}=\dfrac{2}{\sqrt{x^2-y^2}}\left[\Arctan
\left(u\sqrt{\frac{x+y}{x-y}}\right)\right]_0^\infty=\dfrac{\pi}{\sqrt{x^2-y^2}}
.$$
En intégrant par rapport à $x$, on trouve: $\dsp\forall
x>\abs{y},~~f(x,y)=\pi\ln(x+\sqrt{x^2-y^2})+\varphi(y).$
Avec $\varphi$ est une fonction de $\R$ dans $\R$ paire (puisque, pour tout $(x,y)\in \DD$, on a
$f(x,y)=f(x,-y)$).
On admet que $f$ est continue sur $\DD$, donc
$$\forall x>0,~~~~\limiteX{y}{x^-}\,f(x,y)=
\limiteX{y}{x^-}\left(\pi\ln(x+\sqrt{x^2-y^2})+\varphi(y)\right)=\pi\ln(x)+\varphi(x)=f(x,x)=\pi\ln(x)+f(1,1).$$
Ceci montre que $\varphi$ est une fonction constante, comme $f(1,0)=0=\pi\ln(2)+\varphi(0)\Longrightarrow
\varphi=-\pi\ln(2).$
On en déduit, $$\boxed{\dsp\forall (x,y)\in
\DD,~~f(x,y)=\pi\ln\left(\dfrac{x+\sqrt{x^2-y^2}}{2}\right).}$$
Déterminer, pour chacune des fonctions suivantes, le domaine de définition $D_f$. Pour chacune des fonctions, calculer ensuite les dérivées partielles en chaque point du domaine de définition lorsqu'elles existent: $$\mathbf{a\,}\,f(x,y)=x^2\ee^{xy},\quad\mathbf{b\,}\,f(x,y)=\ln(x+\sqrt{x^2+y^2}),\quad\mathbf{c\,}\,f(x,y)=\sin^2 x+ \cos^2y,\quad\mathbf{d)\,} \,f(x,y,z)=x^2y^2\sqrt{z}.$$
- $D_f=\R^2$. $$ \frac{\partial f}{\partial x}(x,y)= 2x\exp(xy)+x^2y\exp(xy),\quad \frac{\partial f}{\partial y}(x,y)= x^3\exp(xy).$$
- $D_f=\{(x,y); x > 0 \ \text{ou} \ y \ne 0\}\subseteq \R^2$. $$\frac{\partial f}{\partial x}(x,y)= \frac{1+\frac{x}{\sqrt{x^2+y^2}}}{x+\sqrt{x^2+y^2}}= \frac 1{\sqrt{x^2+y^2}},\quad \frac{\partial f}{\partial y}(x,y)= \frac{\frac{y}{\sqrt{x^2+y^2}}}{x+\sqrt{x^2+y^2}} =\frac{y}{x\sqrt{x^2+y^2}+x^2+y^2}.$$
- $D_f=\R^2$. $$ \frac{\partial f}{\partial x}(x,y)= 2\sin(x) \cos(x),\quad\frac{\partial f}{\partial y}(x,y)= -2\sin(y) \cos(y).$$
- $D_f=\{(x,y,z); z \ne 0\}\subseteq \R^3$. $$ \frac{\partial f}{\partial x}(x,y,z)= 2xy^2\sqrt{z},\quad \frac{\partial f}{\partial y}(x,y,z)= 2x^2y\sqrt{z} ,\quad \frac{\partial f}{\partial z}(x,y,z)= \frac {x^2y^2}{2\sqrt{z}} .$$
Soit $f : {\R^3} \to \R$ de classe $\CC^1$ telle que
$f(0,1,1) = 0$, $\frac{\partial f}{\partial x}(0,1,1) = 1$, $\frac{\partial f}{\partial y}(0,1,1) = 2$,
$\frac{\partial f}{\partial z}(0,1,1) = 3$.
Peut-on déterminer $\dsp\lim_{t\to0} \frac{f(t^2,\ch t,\ee^t)}{f(t,\cos t,\ch t)}$ ?
Puisque $f$ est de classe $\CC^1$ alors $f$ admet un DL au voisinage de $(0,1,1)$, d'autre part, $$\ch(t)=1+\dfrac{t^2}{2}+\underset{t\to 0}{\mathrm{o}}(t^2),\, \cos(t)=1-\dfrac{t^2}{2}+\underset{t\to 0}{\mathrm{o}}(t^2),\,\ee^t=1+t+\dfrac{t^2}{2}+\underset{t\to 0}{\mathrm{o}}(t^2).$$ Ainsi, en posant $X=(t^2,\ch (t),\ee^t)=(0,1,1)+t(0,0,1)+\underset{t\to 0}{\mathrm{o}}(t)$ et $h=X-(0,1,1)$, $$\begin{array}{lcl} f(X)&=&f(0,1,1)+\frac{\partial f}{\partial x}(0,1,1)\times 0+\frac{\partial f}{\partial y}(0,1,1)\times 0+\frac{\partial f}{\partial z}(0,1,1)\times 1+\underset{\norme{h}\to 0}{\mathrm{o}}(h)\\ &=&3t +\underset{\norme{h}\to 0}{\mathrm{o}}(h) \end{array}$$ On pose maintenant $Y=(t,\cos t,\ch t)=(0,1,1) +t(1,0,0)+\underset{t\to 0}{\mathrm{o}}(t)$ et $h=Y-(0,1,1)$, $$\begin{array}{lcl} f(Y)&=&f(0,1,1)+\frac{\partial f}{\partial x}(0,1,1)\times 1+\frac{\partial f}{\partial y}(0,1,1)\times 0+\frac{\partial f}{\partial z}(0,1,1)\times 0+\underset{\norme{h}\to 0}{\mathrm{o}}(h)\\ &=&t +\underset{\norme{h}\to 0}{\mathrm{o}}(h) \end{array}$$ On en déduit $$\lim_{t\to0} \frac{f(t^2,\ch t,\ee^t)}{f(t,\cos t,\ch t)}=\lim_{t\to0} \frac{3t +\underset{\norme{h}\to 0}{\mathrm{o}}(h)}{t +\underset{\norme{h}\to 0}{\mathrm{o}}(h)}=3.$$
Soit $U$ un ouvert de $\R^n$ et $f\in \CC^2(U,\R)$. On définit $\Delta f$ par $\dsum_{k=1}^n\dfrac{\partial^2\,f}{\partial^2\,x_k}$. Déterminer $\Delta (f)$ dans les cas suivants:
- $f:\R^2\longmapsto\R$ définit par $f(x,y)=\re (z\ee^{-\ii z})$ avec $z=x+\ii y$.
- $f:(\R^*)^3\longmapsto\R$ définit par $f(x,y,z)= \Arctan(y/x)+\Arctan( z/y)+\Arctan (x/z)$.
- Soit $(x,y)\in \R^2$, on a $$ \begin{array}{ll} z\ee^{-\ii z}&= (x+\ii y)\ee^{-\ii (x+\ii y)}=(x+\ii y)\ee^{y-\ii x}\\ &= \ee^{y}(x+\ii y)(\cos(x)-\ii \sin(x))\\ &=\ee^{y}\left(x\cos(x)+y\sin(x)+\ii (y\cos(x)-x\sin(x))\right) \end{array} $$ donc $f(x,y)=\ee^y \left(x\cos(x)+y\sin(x)\right)$. $f$ est de classe $\CC^2$ sur $\R^2$, et on a pour tout $(x,y)\in \R^2$, $$ \dfrac{\partial f}{\partial x}(x,y)=\ee^y\left(\cos(x)-x\sin(x)+y\cos(x)\right),\, \dfrac{\partial f}{\partial y}(x,y)=\ee^y\left(x\cos(x)+y\sin(x)+\sin(x)\right),\, $$ puis, $$ \begin{array}{lcl} \dfrac{\partial^2 f}{\partial x^2}(x,y)&=&\ee^y\left( -\sin(x)-\sin(x)-x\cos(x)-y\sin(x)\right)=\ee^y\left(-2\sin(x) -x\cos(x)-y\cos(x)\right)\\ &&\\ \dfrac{\partial^2 f}{\partial y^2}(x,y)&=&\ee^y\left( x\cos(x)+y\sin(x)+\sin(x) +\sin(x)\right)=\ee^y\left(2\sin(x) +x\cos(x)+y\sin(x)\right) \end{array} $$ On vérifie $$\Delta f =\dfrac{\partial^2 f}{\partial x^2}+\dfrac{\partial^2 f}{\partial y^2}=0.$$ On aurait pu aussi remarque que $$ \dfrac{\partial f}{\partial x}(x,y) =\re \left(\ee^{-\ii z}(1-\ii z)\right), \dfrac{\partial^2 f}{\partial x^2}(x,y)= \re \left(\ee^{-\ii z} (-2\ii-z)\right)$$ de même, $$\dfrac{\partial f}{\partial x}(x,y) =\re \left(\ee^{-\ii z}(\ii+ z)\right), \dfrac{\partial^2 f}{\partial x^2}(x,y)= \re \left(\ee^{-\ii z} (2\ii+z)\right)$$
- $f$ est de classe $\CC^2$ sur $(\R^*)^3$, et pour tout $(x,y,z)\neq (0,0,0)$, on a $$\dfrac{\partial f}{\partial x}(x,y,z)=\dfrac{-y}{x^2}\dfrac{1}{1+y^2/x^2}+\dfrac{1}{z}\dfrac{1}{1+x^2/z^2}=\dfrac{-y}{x^2+y^2}+\dfrac{z}{x^2+z^2}$$ et $$ \dfrac{\partial^2 f}{\partial x^2}(x,y,z)=\dfrac{2xy}{(x^2+y^2)^2}-\dfrac{2xz}{(x^2+z^2)^2}.$$ Vu que $f(y,z,x)=f(x,y,z)$, on en déduit $$ \dfrac{\partial^2 f}{\partial y^2}(x,y,z)= \dfrac{\partial^2 f}{\partial x^2}(y,z,x)=\dfrac{2yz}{(y^2+z^2)^2}-\dfrac{2yx}{(y^2+x^2)^2}.$$ de même, $f(z,x,y)=f(x,y,z)$, $$ \dfrac{\partial^2 f}{\partial z^2}(x,y,z)= \dfrac{\partial^2 f}{\partial x^2}(z,x,y)=\dfrac{2zx}{(z^2+x^2)^2}-\dfrac{2zy}{(z^2+y^2)^2}.$$ Ensuite, $$\Delta f (x,y,z)= \dfrac{2xy}{(x^2+y^2)^2}-\dfrac{2xz}{(x^2+z^2)^2}+ \dfrac{2yz}{(y^2+z^2)^2}-\dfrac{2yx}{(y^2+x^2)^2}+\dfrac{2zx}{(z^2+x^2)^2}-\dfrac{2zy}{(z^2+y^2)^2}=0.$$
Trouver $f\in \CC^2(\R_+^*,\R)$ telle que $\Delta F=0$ avec $F:(\R^*)^n\longmapsto\R$ définit par $F(x_1,\cdots,x_n)=f\left(\sqrt{\dsum_{k=1}^nx_k^2}\right)$.
On suppose que $n>1$, le cas $n=1$ ne présente aucune difficulté.
La fonction $x=(x_1\cdots,x_n)\in \R^n\setminus \{0\}\mapsto \dsum_{k=1}^n x_k^2$ est de classe $\CC^2$
($\CC^\infty$) sur $\R^n\setminus \{0\}$ à valeur dans $\R_+^*$, puis la fonction racine est de classe
$\CC^2$ sur $\R_+^*$, donc $(x_1\cdots,x_n)\mapsto \sqrt{\dsum_{k=1}^n x_k^2}$ est de classe $\CC^2$ sur
$(\R^*)^n$.
Soit $f\in \CC^2(\R_+^*,\R)$, on pose $F(x_1,\cdots,x_n)=f\left(\sqrt{\dsum_{k=1}^nx_k^2}\right)$, alors
$F\in \CC^2((\R^*)^n,\R)$, et pour tout $j\in \inter{1,n}$, on a
$$\dfrac{\partial F}{\partial
x_j}(x_1,\cdots,x_n)=f'\left(\sqrt{\dsum_{k=1}^nx_k^2}\right)\dfrac{x_j}{\sqrt{\dsum_{k=1}^nx_k^2}},$$
$$
\dfrac{\partial^2 F}{\partial x_j^2}(x_1,\cdots,x_n)
=f''\left(\sqrt{\dsum_{k=1}^nx_k^2}\right)\dfrac{x_j^2}{\dsum_{k=1}^nx_k^2}+f'\left(\sqrt{\dsum_{k=1}^nx_k^2}\right)\dfrac{\sqrt{\dsum_{k=1}^nx_k^2}
-\dfrac{x_j^2}{\sqrt{\dsum_{k=1}^nx_k^2}}}{\dsum_{k=1}^nx_k^2}
$$
Afin de simplifier l'écriture, on va notre $r=\sqrt{\dsum_{k=1}^nx_k^2}$. On obtient alors,
$$\Delta F =\dsum_{j=1}^n\dfrac{\partial^2 F}{\partial x_j^2} =\dsum_{j=1}^n
f''(r)\dfrac{x_j^2}{r^2}+f'(r)\dfrac{r^2-x_j^2}{r^3}=f''(r)+f'(r)\dfrac{n-1}{r}.$$
Donc pour que $\Delta F$ soit nulle il faut et il suffit que
$$\forall x>0,\,f''(x)+\dfrac{n-1}{x} f'(x)=0 \Longrightarrow f(x)=\left\{\begin{array}{lcl}
\alpha+\beta x^{2-n},\quad \alpha,\beta\in \R &\text{ si }& n>2,\\
\alpha+\beta \ln(x),\quad \alpha,\beta\in \R &\text{ si }& n=2.
\end{array}
\right.$$
Si $n=2$, alors en cordonnées polaire, on a
$F(x_1,x_2)=f(r)$, et on sait que
$$\Delta F= \dfrac{1}{r}\dfrac{\partial }{\partial r}\left( r\dfrac{\partial F}{\partial r}\right)
+\dfrac{1}{r^2}\dfrac{\partial^2 F}{\partial \theta^2}=f''(r)+\dfrac{1}{r}f'(r).$$
Si $n=3$, en cordonnées sphérique, on a
$$ \Delta F={\frac {\partial ^{2}F}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial F}{\partial
r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}F}{\partial \theta ^{2}}}+{\frac {1}{r^{2}\tan \theta }}{\frac
{\partial F}{\partial \theta }}+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}F}{\partial
\varphi ^{2}}}
$$
Puisque $F$ ne dépend que de $r$, alors on trouve
$$\Delta F ={\frac {\partial ^{2}F}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial F}{\partial r}}
=f''(r)+\dfrac{2}{r}f'(r).$$
EDP
On considère l'équation aux dérivées partielles : $\dfrac{\partial f}{\partial x}(x,y)-\dfrac{\partial f}{\partial y}(x,y)+3(x-y)f(x,y)=0$. On considère également $\fonct{\varphi}{\R^2}{\R^2}{(x,y)}{(xy,x+y)}$
- Montrer que $\varphi$ induit une bijection $\Phi$ de l'ouvert $U=\{(x,y)\in \R^2,\,x-y>0\}$ sur un ouvert $V$ que l'on précisera. Montrer que $\Phi,\,\,\Phi^{-1}$ sont de classe $\CC^1$.
- En déduire les fonctions $f\in \CC^1(U,\R)$ solutions de l'équation (E).
-
Soient $(u,v)\in \R^2$,
$$(u,v)\in \im \Phi \Longleftrightarrow \exists (x,y)\in U,\, \left\{\begin{array}{ll}
xy&=u\\
x+y&=v
\end{array}\right.$$
Ce qui implique que l'équation $X^2-vX+u=0$ admet deux racines distincts (puisque $x-y>0$), donc
$$(u,v)\in \im \Phi \Longleftrightarrow v^2-4u>0\Longleftrightarrow V=\{(u,v)\in \R^2,\,v^2>4u\}.
$$
$\Phi$ est surjective entre $U$ et $V=\im (U)$, montrons qu'elle est injective.
Soient $(x,y),\, (s,t)\in U$ tels que $\Phi (x,y)=\Phi (s,t)= (u,v)$ donc $(x,y)$ (resp. $(s,t)$) sont parmi les solutions de l'équation $X^2-vX+u=0$, i.e. $$(x,y),\,(s,t)\in \left\{\left(\dfrac{v+\sqrt{v^2-4u}}{2} ,\dfrac{v-\sqrt{v^2-4u}}{2}\right),\left(\dfrac{v-\sqrt{v^2-4u}}{2} ,\dfrac{v+\sqrt{v^2-4u}}{2}\right)\right\}$$ Vu que $x-y>0$ et $s-t>0$ alors $x=s,\,y=t$.
On en déduit également, $$\fonct{\Phi^{-1}}{V}{U}{(u,v)}{\left(\dfrac{v+\sqrt{v^2-4u}}{2} ,\dfrac{v-\sqrt{v^2-4u}}{2}\right)}.$$ D'autre part $\Phi$ est de classe $\CC^1$ sur $U$ (fonction polynomiale en les coordonnées de $(x,y)$), et $\Phi^{-1}$ est aussi de classe $\CC^1$ sur $V$ comme la somme, produit et composées des fonctions de classe $\CC^1$. - Soit $f$ une solution de l'EDP. On définit $g$ sur $V$ par $g(u,v)=f(\Phi^{-1}(u,v))=f(x,y)$, alors $g$ est de classe $\CC^1$ sur $V$ et on a $$ \begin{array}{lcl} \dfrac{\partial g}{\partial u}(u,v)&=&\dfrac{\partial f}{\partial x}(x,y)\dfrac{\partial x}{\partial u}+ \dfrac{\partial f}{\partial y}(x,y)\dfrac{\partial y}{\partial u}= \dfrac{-1}{\sqrt{v^2-4u}}\left(\dfrac{\partial f}{\partial x}(x,y)-\dfrac{\partial f}{\partial y}(x,y)\right)\\ &&\\ &=& \dfrac{-1}{\sqrt{v^2-4u}}\left(3(y-x)f(x,y)\right)=3g(u,v) \end{array} $$ On en déduit, que $$\exists h\in \CC^1(\R),\, \forall (u,v)\in V,\quad g(u,v)=\ee^{3u}h(v).$$ Ce qui donne finalement, $$\forall (x,y)\in U,\quad f(x,y)=\ee^{3xy}h(x+y).\quad h\in \CC^1(\R).$$
Trouver les applications $\varphi\in \CC^3(\R_+^*,\R)$ telles que l'application $\fonct{f}{\R^3\setminus\{(0,0,0)\}}{\R}{(x,y,z)}{\varphi(x^2+y^2+z^2)}, \text{vérifie: }$ $$\forall (x,y,z)\in \R^3\setminus\{(0,0,0)\},\quad\,\dfrac{\partial^3\,f}{\partial\,x\partial\,y\partial\,z}(x,y,z)=\dfrac{xyz}{x^2+y^2+z^2}.$$
Soit $\varphi\in \CC^3(\R_+^*,\R)$. On définit
$\fonct{f}{\R^3\setminus\{0\}}{\R}{(x,y,z)}{\varphi(x^2+y^2+z^2)}$, $f$ est de classe $\CC^3$ sur
$\R^3\setminus\{0\}$ (composition des fonctions de classe $\CC^3$).
En dérivant $f$, on trouve:
$$\forall (x,y,z)\neq (0,0,0),~~\dfrac{\partial
^3f}{\partial\,x\partial\,y\partial\,z}(x,y,z)=8xyz\varphi^{(3)}(x^2+y^2+z^2).$$
Ainsi, $f$ vérifie la relation de l'énoncé ssi $\varphi$ vérifie:
$$\forall t\in \R_+^*,~~\varphi^{(3)}(t)=\dfrac{1}{8t}.$$
En intégrant, on trouve:
$$\forall t>0,~~\varphi(t)=\dfrac{1}{16}t^2\ln(t)+At^2+Bt+c,~~~~A,B,C\in \R.$$
Soit $f\in \CC^2(\R^2,\R)$ tel que $\Delta f=0$. On pose: $$\forall (r,t)\in \R^2,\quad g(r,t)=f(r\cos(t),r\sin(t)),\text{ et }, \forall t\in \R,\quad M(r)=\int_0^{2\pi}g(r,t)\ud t.$$
- Montrer que $g$ est de classe $\CC^2$, puis calculer les dérivées partielles de $g$ en fonction de celles de $f$.
- Montrer que $\dsp\dfrac{\partial}{\partial r}\left(r\,\dfrac{\partial \,g}{\partial\,r}\right)=\dfrac{-1}{r}\dfrac{\partial^2\,g}{\partial\,t^2}$.
- Montrer que $M$ est de classe $\CC^2$ sur $\R$. On note $N(r)=rM'(r)$, calculer $N'$.
- En déduire que $M$ est une fonction constante.
- $g$ est de classe $\CC^2$ comme la composée des fonctions de classe $\CC^2$. $$\begin{array}{lcl} \dfrac{\partial g}{\partial\,r}&=&\cos(t)\dfrac{\partial f}{\partial\,x}+\sin(t)\dfrac{\partial f}{\partial\,y},~~~~ \dfrac{\partial g}{\partial\,t}=-r\sin(t)\dfrac{\partial f}{\partial\,x}+r\cos(t)\dfrac{\partial f}{\partial\,y}.\\ &&\\ \dfrac{\partial^2 g}{\partial\,r^2}&=&\cos^2(t)\dfrac{\partial^2 f}{\partial\,x^2}+2\cos(t)\sin(t)\dfrac{\partial^2 f}{\partial\,x\partial\,y}+\sin^2(t)\dfrac{\partial^2 f}{\partial\,y^2}\\ &&\\ \dfrac{\partial^2 g}{\partial\,t^2}&=&-r\dfrac{\partial g}{\partial\,r}+r^2\left(\sin^2(t)\dfrac{\partial^2 f}{\partial\,x^2}-2\cos(t)\sin(t)\dfrac{\partial^2 f}{\partial\,x\partial\,y}+\cos^2(t)\dfrac{\partial^2 f}{\partial\,y^2} \right).\end{array} $$ Ce qui donne, en tenant compte que $\Delta f=0$, $$r^2\Delta f=0=r^2\dfrac{\partial^2 g}{\partial\,r^2}+r\dfrac{\partial g}{\partial\,r}+\dfrac{\partial^2 g}{\partial\,t^2}\Longrightarrow\dfrac{\partial}{\partial\,r}\left(r\dfrac{\partial g}{\partial r}\right)=-\dfrac{1}{r}\dfrac{\partial^2 g}{\partial\,t^2}.$$
-
La fonction $g$ est de classe $\CC^2$, d'après le théorème sur les intégrale dépendant d'un
paramètre, on a $M$ est également de classe $\CC^2$. De plus,
$$\forall r\in \R,~~M'(r)=\int_0^{2\pi}\dfrac{\partial g}{\partial\,r}(r,t)\ud t\Longrightarrow
rM'(r)=\int_0^{2\pi}r\dfrac{\partial g}{\partial\,r}(r,t)\ud t.$$
La fonction $N$ est également dérivable, et on a:
$$\forall r\in \R,~~N'(r)=\int_0^{2\pi}\dfrac{\partial}{\partial\,r}\left(\dfrac{\partial
g}{\partial\,r}\right)(r,t)\ud t=\dfrac{-1}{r^2}\int_0^{2\pi}\dfrac{\partial^2
g}{\partial\,t^2}(r,t)\ud t=0.$$
Car la fonction $t\longmapsto \dfrac{\partial g}{\partial t}(r,t)$ est $2\pi$-périodique.
On en déduit que la fonction $N$ est constante, de plus comme $N(0)=0$, on trouve alors $N=0$. D'où, la fonction $M$ est constante sur $\R$.
On considère l'équation aux dérivées partielles : $$\dfrac{\partial f}{\partial u}(u,v)+2u\dfrac{\partial f}{\partial v}(u,v)=0 \quad(\EE)$$
- Montrer que l'application $\varphi: (x,y) \mapsto (x,y+x^2)$ est bijective de $\R^2$ sur $\R^2$ et que $\varphi$ et son inverse sont de classe $\CC^1$.
- À l'aide d'un changement de fonction inconnue, déterminer toutes les solutions de $(\EE)$ de classe $\CC^1$ sur $\R^2$.
- Il est clair que $\varphi$ est bijective donc la fonction inverse est $\fonct{\varphi^{-1}}{\R^2}{\R^2}{(u,v)}{(u,v-u^2)}$. De plus $\varphi$ et $\varphi^{-1}$ sont des fonctions de classe $\CC^1$ sur $\R^2$ (fonctions polynomiales par rapport aux coordonnées).
-
On pose $f^*(x,y)=f(\varphi(x,y))$.
$$\dfrac{\partial f^*}{\partial\,x}=\dfrac{\partial f}{\partial\,u}\dfrac{\partial
u}{\partial\,x}+\dfrac{\partial f}{\partial\,v}\dfrac{\partial v}{\partial\,x}=\dfrac{\partial
f}{\partial\,u}+2u\dfrac{\partial f}{\partial\,v}.$$
Ainsi, si $f$ est une solution de $(\EE)$ alors $f^*$ vérifie $\dfrac{\partial
f^*}{\partial\,x}=0$. En intégrant cette équation on trouve $f^*(x,y)=g(y)$ ou $g\in
\CC^1(\R)$.
On en déduit que l'ensemble de solution de $(\EE)$ est $\{(u,v)\longmapsto g(v-u^2),~~g\in \CC^1(\R,\R)\}$.
Trouver les applications de classe $\CC^1$, sur un ouvert de $\R^2$ à préciser, vérifiant: $$(\EE):\quad \quad z\left(x\dfrac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}\right)+x^2+y^2=0.$$ On pourra passer en coordonnées polaires.
Soit $\Omega=\R_2\setminus \{(x,0),~~x\leq 0\}$. On considère le changement de variable
$$\fonct{\varphi}{\Omega'=\R_+^*\times ]-\pi,\pi[}{\Omega}{(r,\theta)}{(r\cos(\theta),r\sin(\theta))}.$$
$\varphi$ est un difféomorphisme de $\Omega'$ dans $\Omega$.
Si $z\in \CC^1(\Omega,\R)$, on pose $z^*=z\circ\varphi$. $z^*\in \CC^1(\Omega',\R)$ et on a:
$$x\dfrac{\partial z}{\partial\,x}(x,y)+\dfrac{\partial z}{\partial\,y}(x,y)=r\dfrac{\partial
z^*}{\partial\,r}(r,\theta).$$
Donc l'équation $(\EE)$ est transformée en $(\EE'):~~z^*\dfrac{\partial z^*}{\partial\,r}+r=0$ sur
$\Omega'$.
On intègre l'équation $(\EE')$, ce qui donne $(z^*)^2+r^2=h(\theta)$ avec $h\in
\CC^1(]-\pi,\pi[,]r,\infty[)$.
On note pour $R\in \R_+^*$, $\Omega_R=\{(x,y)\in \R^2,~~x^2+y^2< R\}\setminus(\R_-\times\{0\})$. Les
solutions de $(\EE)$ sont donc de la forme:
$$z(x,y)=\epsilon\sqrt{h\left(\frac{y}{x+\sqrt{x^2+y^2}}\right)-(x^2+y^2)},\,\epsilon\in \{-1,1\},~~h\in
\CC^1(\R,]R,\infty[).$$
On note $U=\{(x,y)\in \R^2,\,y>\abs{x}\}$. Trouver les applications $f\in \CC^2(U,\R)$ telles que: $$\forall (x,y)\in U,~~\dfrac{\partial^2\,f}{\partial\,x^2}(x,y)-\dfrac{\partial^2\,f}{\partial\,y^2}(x,y)=\dfrac{1}{\sqrt{y^2-x^2}}.$$ En utilisant le changement de variable $u=x+y$ et $v=y-x$.
Considérons l'application $\fonct{\varphi}{U}{\R^2}{(x,y)}{(x+y,y-x)}$, d'après la définition de $U$, on
a $\varphi(U)=V=(\R_+^*)^2$.
Il est clair que $\varphi$ est $\CC^2$- difféomorphisme de $U$ sur $V$.
Soit $f\in \CC^2(U,\R)$, on définit $F\in \CC^2(V,\R)$ telle que $f(x,y)=F(u,v)$. On a
$$\left\{\begin{array}{lclcl}
\dfrac{\partial f}{\partial\,x}&=&
\dfrac{\partial F}{\partial\,u}\dfrac{\partial u}{\partial\,x}+\dfrac{\partial
F}{\partial\,v}\dfrac{\partial v}{\partial\,x}&=&\dfrac{\partial F}{\partial\,u}-\dfrac{\partial
F}{\partial\,v}.\\
&&&&\\
\dfrac{\partial f}{\partial\,y}&=&
\dfrac{\partial F}{\partial\,u}\dfrac{\partial u}{\partial\,y}+\dfrac{\partial
F}{\partial\,v}\dfrac{\partial v}{\partial\,y}&=&\dfrac{\partial F}{\partial\,u}+\dfrac{\partial
F}{\partial\,v}.
\end{array}
\right.$$
Ensuite, on calcul les dérivées partielles d'ordre 2 (on utilise aussi le théorème de Schwarz):
$$
\left\{\begin{array}{lclcl}
\dfrac{\partial^2 f}{\partial\,x^2}&=&
\dfrac{\partial^2 F}{\partial\,u^2}-\dfrac{\partial^2 F}{\partial v\,\partial\,u}-\dfrac{\partial^2
F}{\partial \,v\partial\,u}+\dfrac{\partial^2 F}{\partial\,v^2}&=&\dfrac{\partial^2
F}{\partial\,u^2}-2\dfrac{\partial^2 F}{\partial\,u\partial\,v}+\dfrac{\partial^2 F}{\partial\,v^2}\\
&&&&\\
\dfrac{\partial^2 f}{\partial\,y^2}&=&
\dfrac{\partial^2 F}{\partial\,u^2}+\dfrac{\partial^2 F}{\partial v\,\partial\,u}+\dfrac{\partial^2
F}{\partial \,v\partial\,u}+\dfrac{\partial^2 F}{\partial\,v^2}&=&\dfrac{\partial^2
F}{\partial\,u^2}+2\dfrac{\partial^2 F}{\partial\,u\partial\,v}+\dfrac{\partial^2 F}{\partial\,v^2}
\end{array}
\right.
$$
Ainsi, si $f$ est une solution de l'équation, on trouve que $F$ vérifie l'équation suivante:
$$\forall (u,v)\in V,~~~~-4\dfrac{\partial^2 F}{\partial\,u\partial\,v}=\dfrac{1}{\sqrt{uv}}.$$
En intégrant cette dernière équation par rapport à $u$ ($v$ est fixe), on trouve:
$$\forall (u,v)\in V,~~~~\dfrac{\partial
F}{\partial\,v}=\dfrac{-1}{2}\dfrac{\sqrt{u}}{\sqrt{v}}+h(v),~~h\in \CC^1(\R_+^*,\R).$$
On intègre à nouveau par rapport à $v$, on obtient,
$$\forall (u,v)\in V,~~F(u,v)=-\sqrt{uv}+H(v)+L(u),~~H,L\in \CC^2(\R_+^*,\R).$$
On en déduit l'ensemble de solutions de l'EDP est:
$$\boxed{\left\{(x,y)\in U\longmapsto -\sqrt{y^2-x^2}+A(x+y)+B(y-x),~~~~A,B\in
\CC^2(\R_+^*,\R)\right\}}.$$
On dit que $f$, continue de $\R^3$ dans $\R$, est $\alpha$-positivement homogène s'il existe $\alpha\in \R$, tel que $$\forall (x,y,z)\in \R^3,\forall \lambda\in \R_+^*,\quad f(\lambda x,\lambda y,\lambda z)=\lambda^\alpha f(x,y,z).$$ Montrer que $f$, de classe $\CC^1$ est $\alpha$-positivement homogène ssi $$\forall (x,y,z)\in \R^3,\quad x\dfrac{\partial f}{\partial x}(x,y,z)+y\dfrac{\partial f}{\partial y}(x,y,z)+z\dfrac{\partial f}{\partial z}(x,y,z)=\alpha f(x,y,z).$$
Soit $f\in \CC^1(\R^3,\R)$ vérifiant l'équation suivante:
$$\forall (x,y,z)\in \R^3,\quad x\dfrac{\partial f}{\partial x}(x,y,z)+y\dfrac{\partial f}{\partial
y}(x,y,z)+z\dfrac{\partial f}{\partial z}(x,y,z)=\alpha f(x,y,z).$$
Soit $(x,y,z)\in \R^3$. On définit alors sur $\R_+^*$ la fonction, $g(t)=f(tx,ty,tz)$,
$g$ est de classe $\CC^1$ sur $\R$ comme le produit et la composées des fonctions de classe $\CC^1$, de
plus,
$$\begin{array}{lcl}
\forall t>0,\quad g'(t)&=&\left(x\dfrac{\partial f}{\partial x}(tx,ty,tz)+y\dfrac{\partial f}{\partial
y}(tx,ty,tz)+z\dfrac{\partial f}{\partial z}(tx,ty,tz)\right)\\
&=&\dfrac{1}{t}\left(tx\dfrac{\partial f}{\partial x}(tx,ty,tz)+ty\dfrac{\partial f}{\partial
y}(tx,ty,tz)+tz\dfrac{\partial f}{\partial z}(tx,ty,tz)\right)\\
&=&\dfrac{\alpha f(tx,ty,tz)}{t}=\dfrac{\alpha}{t}g(t)
\end{array}$$
On en déduit, qu'il existe $K\in \R$ tel que $g(t)=K t^\alpha$, comme $g(1)=f(x,y,z)$ alors $K=f(x,y,z)$
ce qui donne,
$$\forall t>0,\, g(t)=t^\alpha f(x,y,z)=f(tx,ty,tz).$$
Ce qui prouve que $f$ est $\alpha$-positivement homogène.
Inversement, supposons que $f$ (de classe $\CC^1$) est $\alpha$-positivement homogène. Soit $(x,y,z)\in
\R^3$, on définit, $g(t)=f(tx,ty,tz)$ et $h(t)=t^\alpha f(x,y,z)$, $g$ et $h$ sont de classe $\CC^1$ sur
$\R_+^*$ et par hypothèse d=sur $f$, on a $g=h$.
En dérivant les deux fonction, on obtiens
$$g'(t)=\left(x\dfrac{\partial f}{\partial x}(tx,ty,tz)+y\dfrac{\partial f}{\partial
y}(tx,ty,tz)+z\dfrac{\partial f}{\partial z}(tx,ty,tz)\right)=h'(t)=\alpha t^{\alpha-1}f(x,y,z).$$
Ensuite, on prend $t=1$, ce qui donne
$$x\dfrac{\partial f}{\partial x}(x,y,z)+y\dfrac{\partial f}{\partial y}(x,y,z)+z\dfrac{\partial
f}{\partial z}(x,y,z)=\alpha f(x,y,z).$$
Théorème de fonction implicite
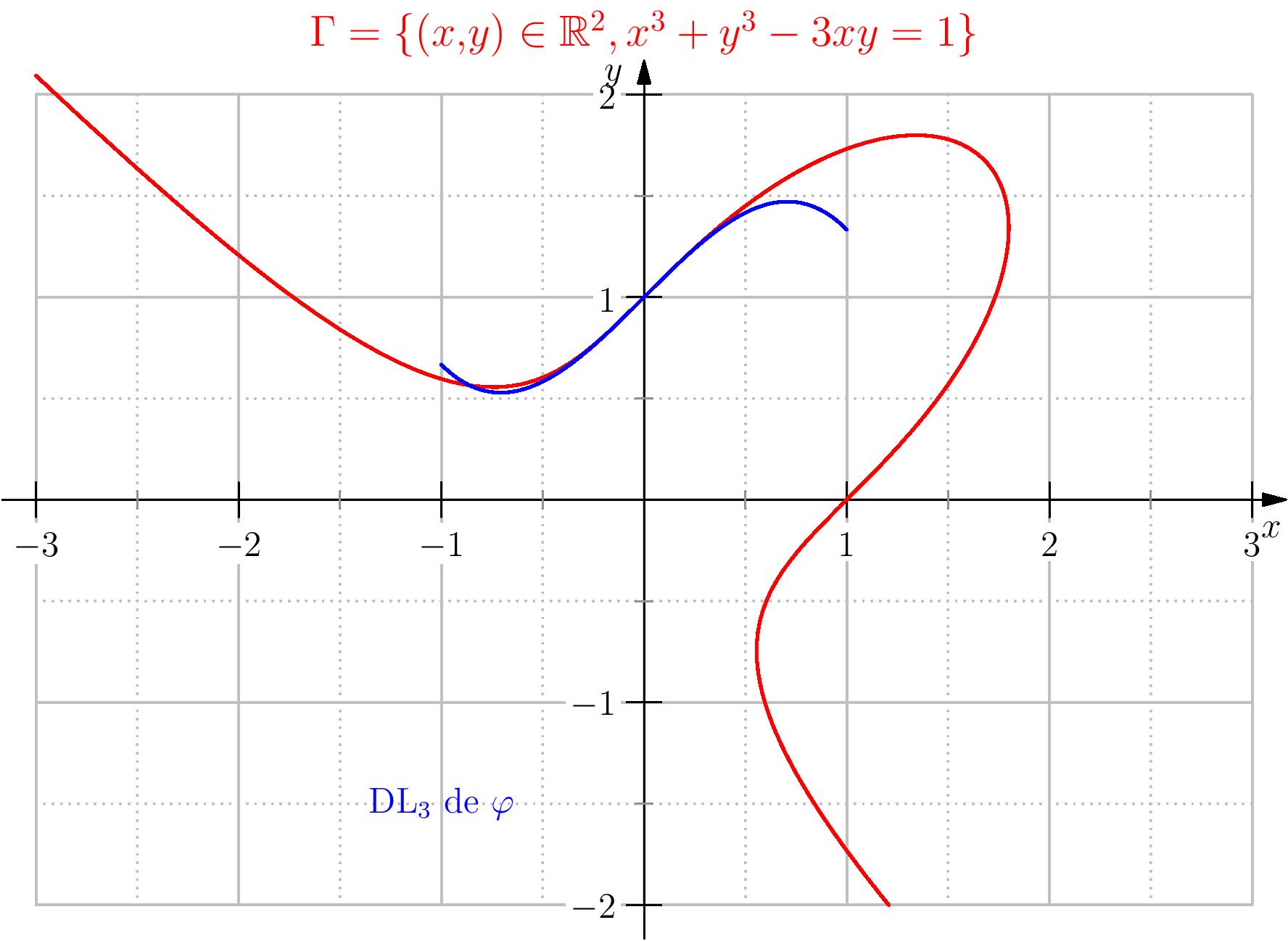
Montrer que l'équation $f(x,y)=x^3+y^3-3xy-1=0$ définit implicitement au voisinage de $0$ une fonction $\varphi$ telle que $\varphi(0)=1$ puis donner le développement limité à l'ordre $3$ de $\varphi$.
La fonction $f$ est de classe $\CC^\infty$ sur $\R^2$, et
$$\dfrac{\partial f}{\partial x}(x,y)=3x^2-3y,\quad \dfrac{\partial f}{\partial y}(x,y)=3y^2-3x.$$
Puisque $f(0,1)=1-1=0$ et $\dfrac{\partial f}{\partial y}(0,1)=3$.
Le théorème du cours, assure alors qu'il existe un voisinage $I$ de $0$ et une fonction $\varphi$ de $I$
dans $\R$, tel que
$$\varphi (0)=1,\, \,\forall x\in I,\quad f(x,\varphi(x))=0.$$
De plus, $\varphi$ est de dérivable sur $I$ et
$$\forall x\in I,\quad \varphi'(x)=\dfrac{-\partial_x f(x,\varphi(x))}{\partial_y f(x,\varphi(x))},\,
\,\text{ en particulier } \varphi'(0)=1.$$
On admet que $\varphi$ est de classe $\CC^\infty$ sur $I$, et on pose
$\varphi(x)=1+x+bx^2+cx^3+\mathrm{o}(x^3)$, on remplace dans la relation précédente,
$$
\begin{array}{lcl}
0&=&f(x,\varphi(x))\\
&=&x^3+(1+x+bx^2+cx^3+\mathrm{o}(x^3))^3-3x(1+x+bx^2+cx^3+\mathrm{o}(x^3))-1\\
&=&x^3+(1+3x+(3+3b)x^2+(1+6b+3c)x^3)-3x-3x^2-3bx^3-1+\mathrm{o}(x^3)\\
&=&3bx^2+(2+3b+3c)x^3+\mathrm{o}(x^3)
\end{array}
$$
Ainsi, $b=0,\, c=-\dfrac{2}{3}$, on en déduit alors
$$\varphi (x) = 1+x-\dfrac{2}{3}x^3+\underset{x\to 0}{\mathrm{o}}(x^3).$$
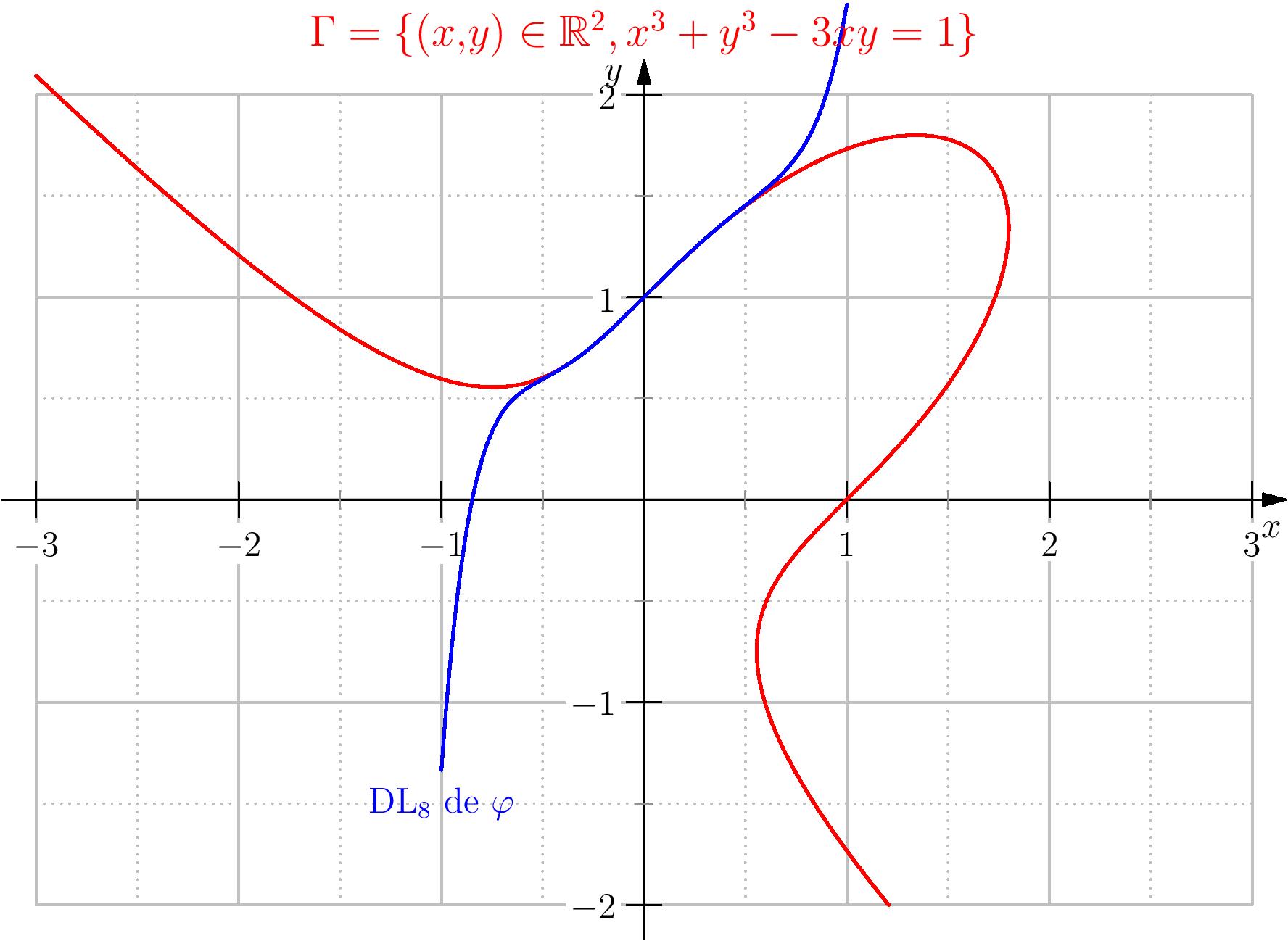
\textit{Remarque:} On peut (en utilisant la même méthode), trouver un DL de $\varphi$, pour les
courageux!
$$\varphi (x) = 1+x-\dfrac{2}{3}x^3+\dfrac{2}{3}x^4-\dfrac{10}{9}x^6+\dfrac{14}{9}x^7+\underset{x\to
0}{\mathrm{o}}(x^8).$$
|
|
$\quad$ |
|
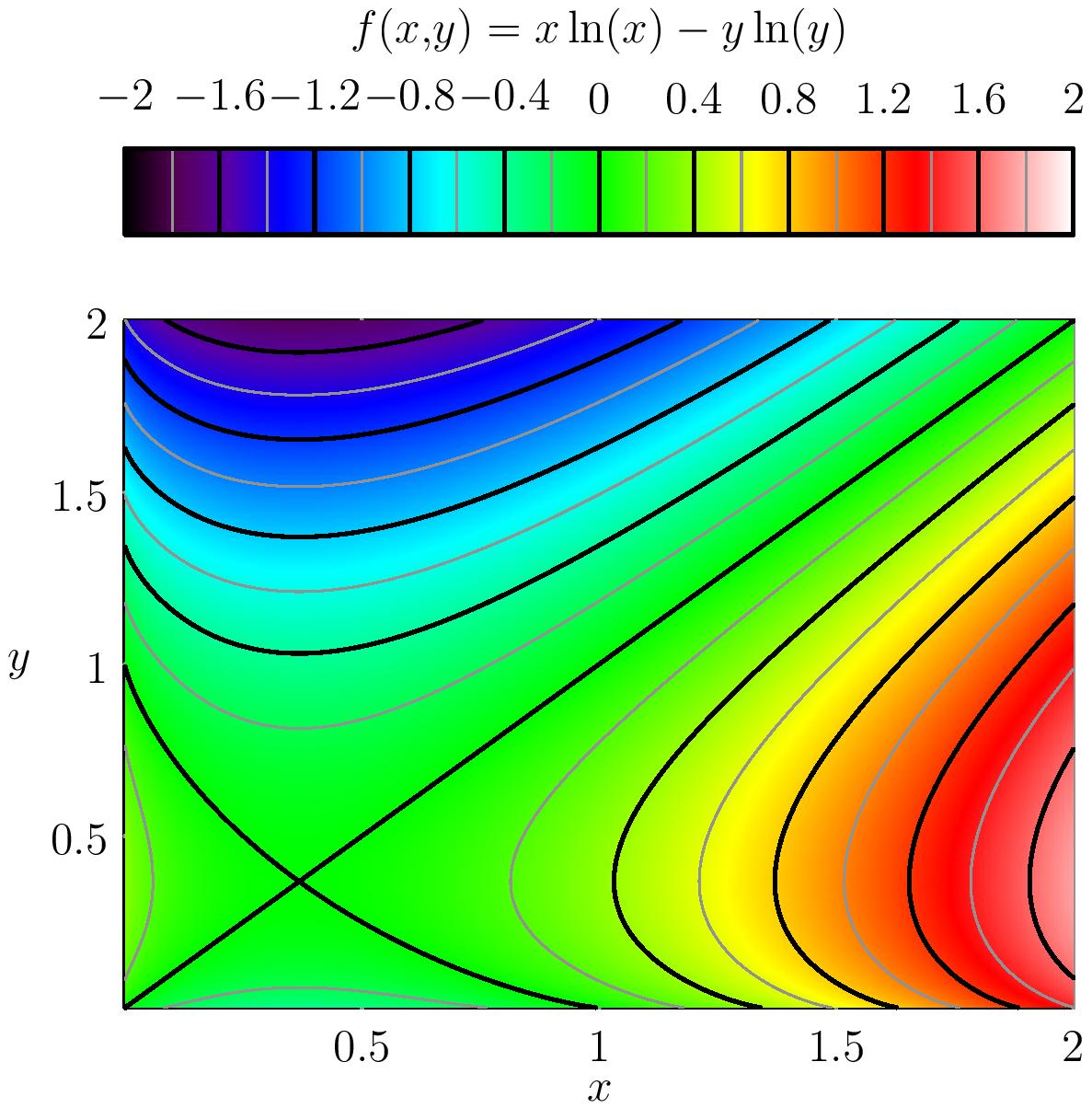
Soit $f(x,y) = x\ln x - y\ln y$ $(x,y > 0)$. Pour $k \in \R$, on considère la courbe $\mathcal{C}_k$ d'équation $f(x,y) = k$.
- Suivant la position de $(a,b) \in \mathcal{C}_k$, préciser l'orientation de la tangente à $\mathcal{C}_k$ en $(a,b)$.
- Dresser le tableau de variations de $\phi(t) = t\ln t$.
- Dessiner $\mathcal{C}_0$. (\'Etudier en particulier les points $(0,1), (1,0)$ et $\Bigl(\frac 1e,\frac 1e\Bigr)$ à l'aide de DL)
- Indiquer l'allure générale des courbes $\mathcal{C}_k$ suivant le signe de $k$.
voir fichiers Lniveau.pdf et XLNX.pdf sur Eclat
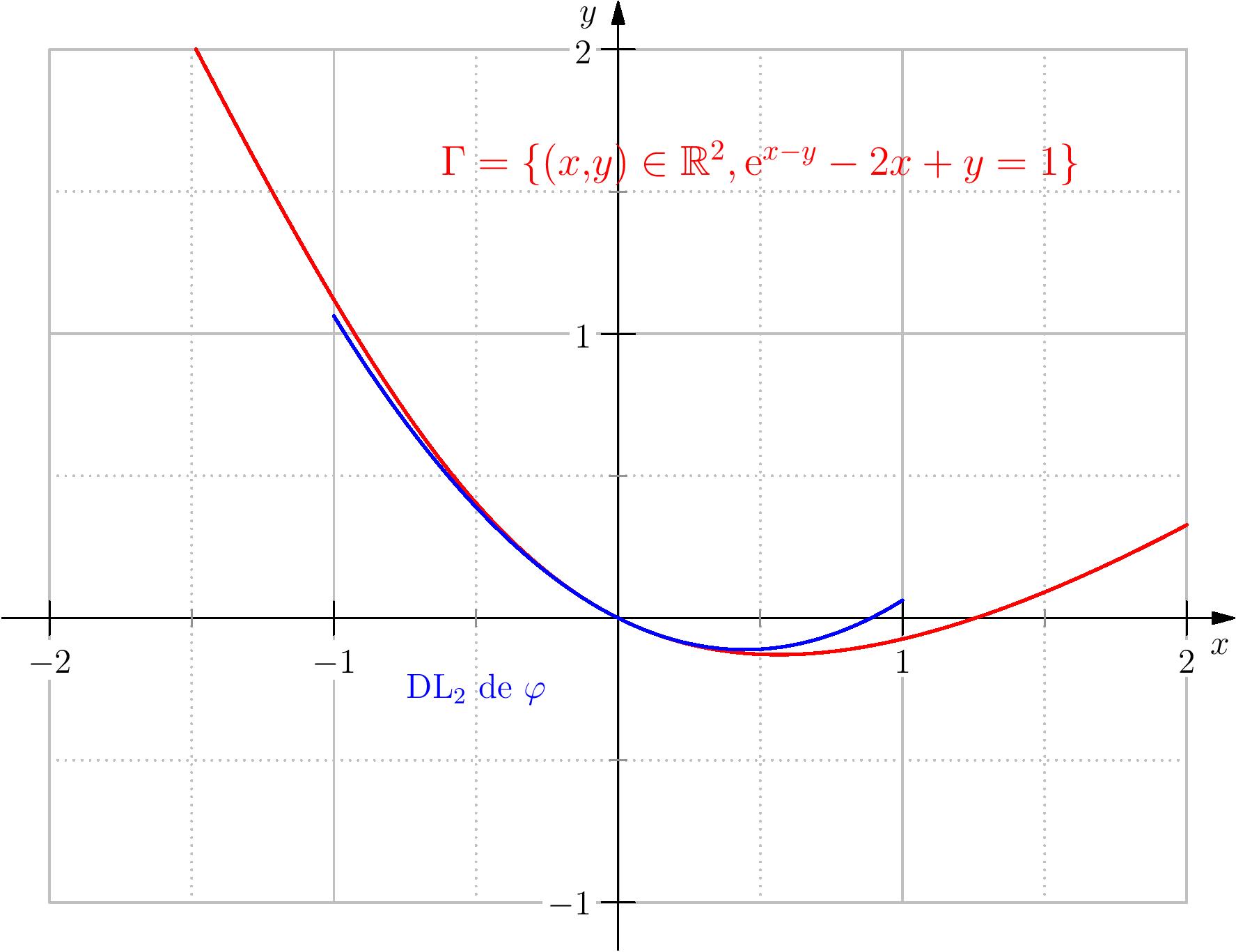
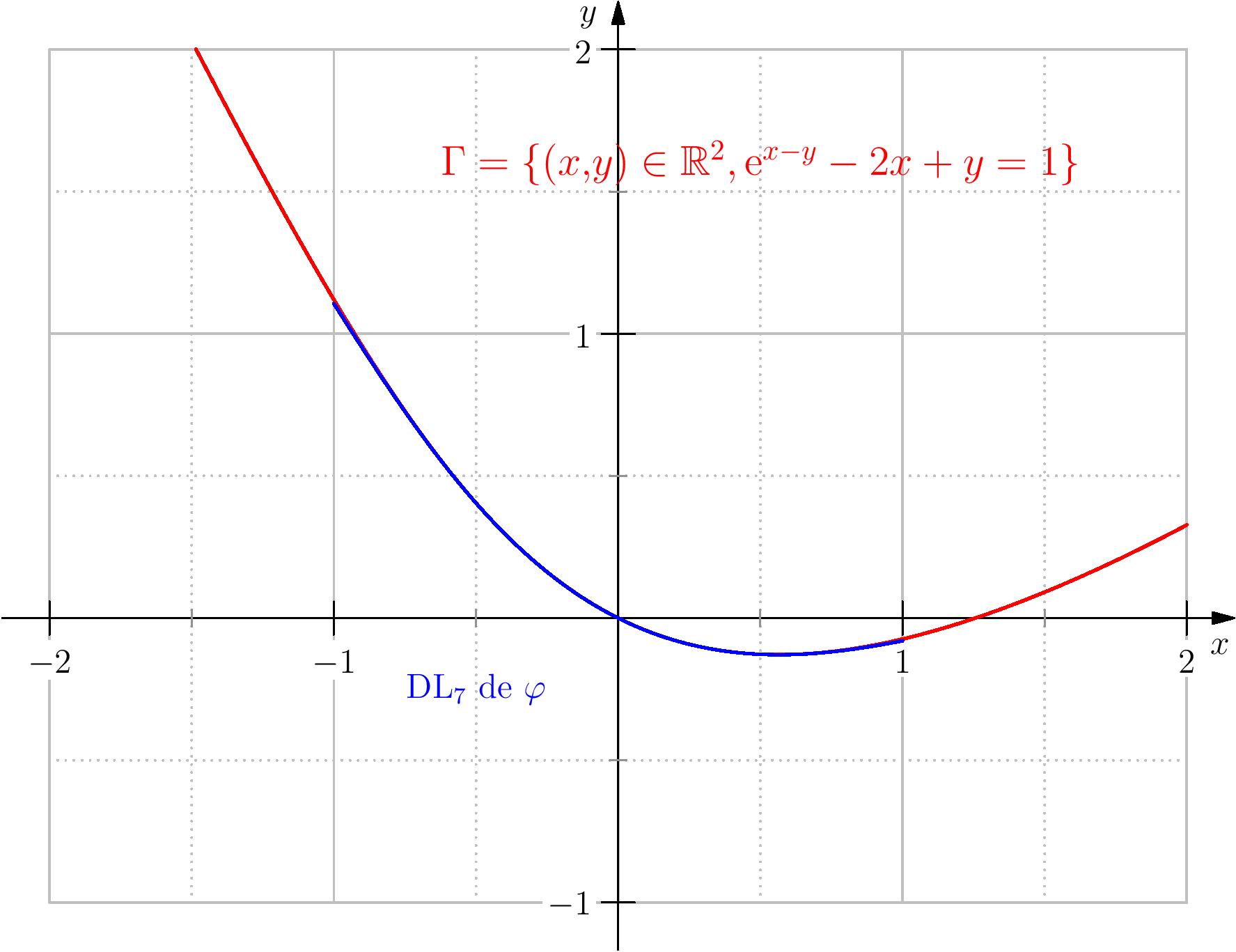
On considère la courbe d'équation $\ee^{x-y} = 1+2x+y$. Donner la tangente à cette courbe et la position par rapport à la tangente au point $(0,0)$.
On pose $f(x,y)=\ee^{x-y}-1-2x-y$, la fonction $f$ est de classe $\CC^\infty$ sur $\R^2$, et
$$\dfrac{\partial f}{\partial x}(x,y)=\ee^{x-y}-2,\quad \dfrac{\partial f}{\partial
y}(x,y)=-\ee^{x-y}-1.$$
Puisque $f(0,0)=0$ et $\dfrac{\partial f}{\partial y}(0,0)=-2\neq 0$, le théorème du cours, assure alors
qu'il existe un voisinage $I$ de $0$ et une fonction $\varphi$ de $I$ dans $\R$, tel que
$$\varphi (0)=0,\, \,\forall x\in I,\quad f(x,\varphi(x))=0.$$
De plus, $\varphi$ est de dérivable sur $I$ et
$$\forall x\in I,\quad \varphi'(x)=\dfrac{-\partial_x f(x,\varphi(x))}{\partial_y f(x,\varphi(x))},\,
\,\text{ en particulier } \varphi'(0)=\dfrac{-1}{2}.$$
On admet que $\varphi$ est de classe $\CC^\infty$ sur $I$, et on pose
$\varphi(x)=-x/2+bx^2+\mathrm{o}(x^2)$, on remplace dans la relation précédente,
$$
\begin{array}{lcl}
0&=&f(x,\varphi(x))\\
&=&\ee^{3x/2-bx^2+\mathrm{o}(x^2)}-1-2x+x/2-bx^2+\mathrm{o}(x^2)\\
&=&1+3x/2+(9/8-b)x^2-1-3/2x-bx^2+\mathrm{o}(x^2)\\
&=&(9/8-2b)x^2+\mathrm{o}(x^3)
\end{array}
$$
Donc $\varphi(x) = -\frac x2 + \frac {9x^2}{16} + o (x^2) \Rightarrow {}$
tangente de pente $-\frac 12$, au dessus.
|
|
$\quad$ |
|
Extremums
Déterminer les extremums (éventuels) de la fonction $f$ définie sur $\R^2$ par: $$\forall (x,y)\in\R^2,~~~~f(x,y)=x^3+3xy-15x-12y.$$
$f$ est de classe $\CC^\infty$ sur $\R^2$, donc les extremums (éventuels) sont parmi ses points
critiques.
Pour déterminer les points critiques, on calcule les dérivées partielles de $f$,
$$
\left.
\begin{array}{ll}
\dfrac{\partial f}{\partial x}(x,y)&=3x^2+3y-15\\
&\\
\dfrac{\partial f}{\partial y}(x,y)&=3x-12
\end{array}\right\}\Longrightarrow \dfrac{\partial f}{\partial x}(x,y)=\dfrac{\partial f}{\partial
y}(x,y)=0 \text{ ssi } x=4,y=-11.$$
Soient $u,v\in \R$ (assez proches de $0$), on a
$$
\begin{array}{lcl}
f(4+u,-11+v)-f(4,-11)&=&(4+u)^3+3(4+u)(-11+v)-15(4+u)-12(-11+v)-4\\
&=&12u^2+3uv+u^3\\
&=&3 \left(\left(2u+\frac{v}{4}\right)^2-\dfrac{v^2}{16}\right)+u^3.
\end{array}
$$
Pour $v=0$, on a
$$f(4+u,-11)-f(4,-11)=12u^2+u^3\geq 0 $$
et pour $v=-8u$, on a
$$f(4+u,-11-8u)-f(4,-11)=-12u^2+u^3\leq 0$$
On en déduit que le point $(4,-11)$ n'est pas un extremum de $f$. Donc $f$ n'a pas d'extremums.
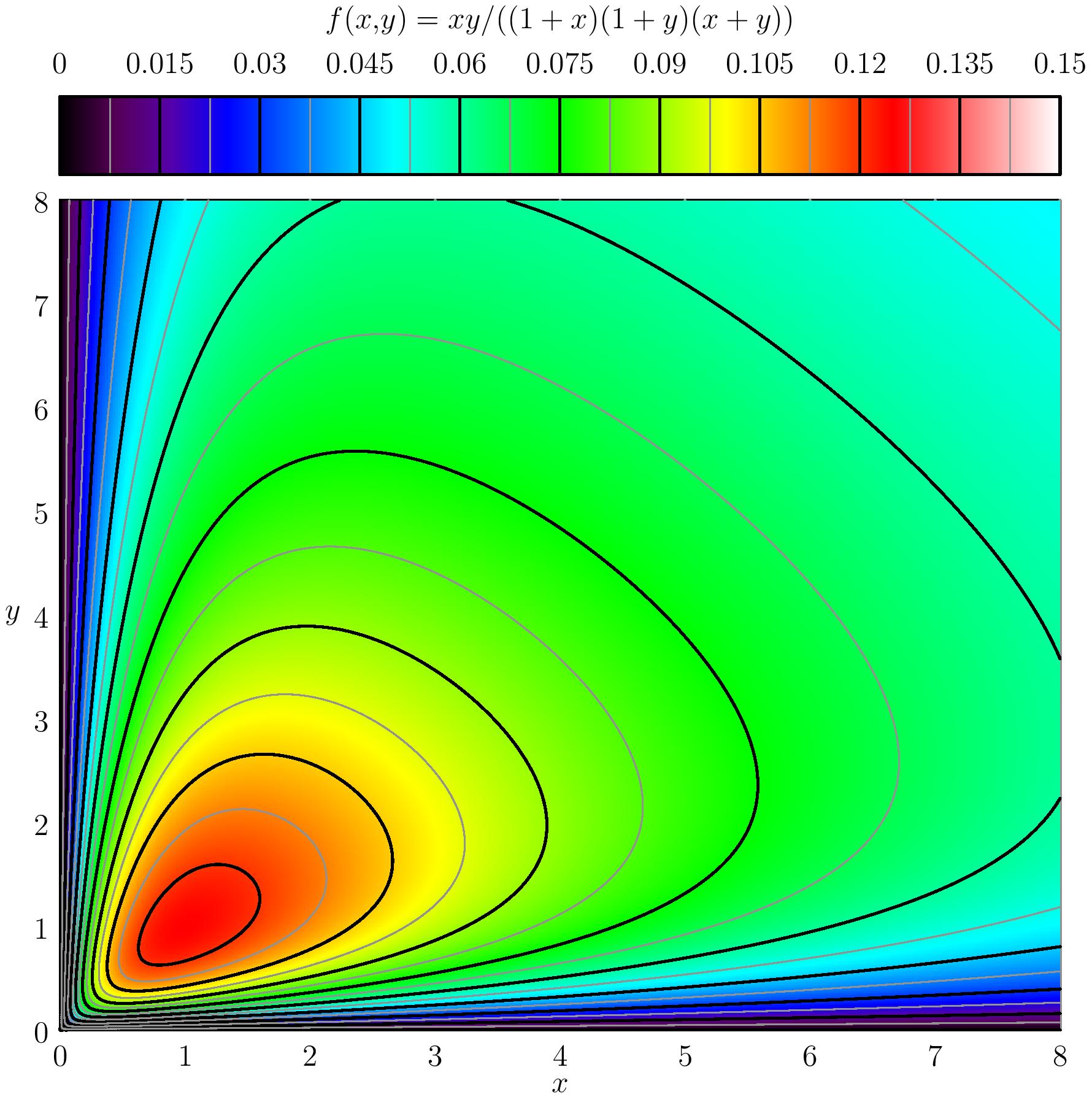
Montrer que $f(x,y)=\dfrac{xy}{(1+x)(1+y)(x+y)}$ pur $(x,y)\neq (0,0)$ et $f(0,0)=0$ est continue sur $(\R_+)^2$. Déterminer les extrema de $f$ sur $(\R_+)^2$.
Il est clair que $f$ est continue sur $\R_+^2\setminus\{(0,0)\}$ comme le quotient de deux fonctions
continues.
Il reste à montrer que $f$ est continue en $(0,0)$, pour cela il suffit de montrer que $\dsp\lim_{X\to
(0,0)} f(X)=0$
(avec $X=(x,y)$). On munit $\R^2$ de la norme $\norme{X}=\abs{x}+\abs{y}$.
Soit $X=(x,y)\in \R_+^2$ non nul, alors $1+x>1,\,1+y>1$, $x+y=\norme{X}$ et on a aussi $xy\leq
\norme{X}^2$, ce qui donne,
$$\abs{f(X)-f((0,0))}=\dfrac{xy}{(1+x)(1+y)(x+y)}\leq \dfrac{xy}{x+y}\leq
\norme{X}\tendvers{X}{(0,0)}\,0$$
Ce qui prouve la continuité de $f$ en $(0,0)$.
On remarque aussi que $f(x,y)\geq 0$ sur son domaine de définition, et
$$\forall x\geq 0,\,\forall y\geq 0,\quad f((x,0))=f((0,y))=0.$$
On en déduit que $f$ admet un minimum globale.
Notons $\Omega=(\R_+^*)^2$. L fonction $f$ est de classe $\CC^1$ sur $\Omega$, donc les éventuels
extremums de $f$ vérifient les conditions nécessaires $\dfrac{\partial f}{\partial
x}(x,y)=\dfrac{\partial f}{\partial y}(x,y)=0$, or
$$\dfrac{\partial f}{\partial
x}(x,y)=\dfrac{y}{1+y}\dfrac{(1+x)(x+y)-x(1+2x+y)}{(1+x)^2(x+y)^2}=\dfrac{y}{1+y}\dfrac{y-x^2}{(1+x)^2(x+y)^2}.$$
En remarquant que $f(y,x)=f(y,x)$, on trouve $\dfrac{\partial f}{\partial
y}(x,y)=\dfrac{x}{1+x}\dfrac{x-y^2}{(1+y)^2(x+y)^2}.$
Ainsi le seul point critique de $f$ dans $\Omega$ est le point $(1,1)$.Il faut maintenant regarder le
signe de $f(x,y)-f(1,1)$, on pose $x=1+a,\,y=1+b$ avec $a$ et $b$ au voisinage de $0$,
$$\begin{array}{lcl}
f(1+a,1+b)&=&\dfrac{(1+a)(1+b)}{(2+a)(2+b)(2+a+b)}=\dfrac{1+(a+b)+ab}{8(1+a/2)(1+b/2)(1+(a+b)/2)}\\
&=&\dfrac{1+(a+b)+ab}{8(1+(a+b)+ab/4+(a+b)^2/4+ab(a+b)/8)}\\
&=&\dfrac{1}{8}\left(1+(a+b)+ab\right)\left(1-(a+b)-ab/4-(a+b)^2/4+(a+b)^2+\mathrm{o}(r^2)\right)\\
&=&(1/8)\Big(1+(a+b)+ab-(a+b)-(a+b)^2-ab/4-(a+b)^2/4+(a+b)^2+\mathrm{o}(r^2)\Big)\\
&=&(1/8)\big(1+3ab/4-(a+b)^2/4+\mathrm{o}(r^2)\Big)
\end{array}$$
Remarque: Dans le DL on s'arrête à l'ordre 2, i.e. $a^2$, $ab$ ou $b^2$.
Il n'y pas de terme d'ordre $1$ ce qui est normal puisque le point $(1,1)$ et un point critique.
Enfin, j'ai noté $r^2=a^2+b^2$.
On en déduit,
$$f(1+a,1+b)-f(1,1)=\dfrac{-1}{32}\Big(a^2+b^2-ab\big)+\mathrm{o}(r^2)=\dfrac{-1}{32}\left(\left(a-\frac{b}{2}\right)^2+\frac{3b^2}{4}\right)+\mathrm{o}(r^2)\leq
0.$$
On en déduit que $f$ admet un maximum local en $(1,1)$. Reste à savoir s'il s'agit d'un maximum globale.
Pour cela, on considère $\Omega_1=\{(x,y)\in \R_+^2,\,x+y> 8\}$, on a pour tout $(x,y)\in \Omega_1$,
$$\,f(x,y)=\dfrac{x}{1+x}\dfrac{y}{1+y}\dfrac{1}{x+y}< \dfrac{1}{8}=f(1,1).$$
L'ensemble $\R_+^2\setminus\Omega_1$ est un fermé borné de $\R^2$, ainsi d'après le cours, $f$ admet un
maximum sur cet ensemble, et d'après l'étude précédente, ce maximum ne peut être atteint que au point
critique $(1,1)$.
Conclusion, $f$ admet un maximum globale en $(1,1)$.
Soit $a>0$, et $\fonct{f}{(\R_+^*)^2}{\R}{(x,y)}{\dfrac{a}{x}+\dfrac{a}{y}+\dfrac{xy}{a^2}}$. Montrer que $f$ possède un minimum global que l'on détermine(ra).
$f$ est de classe $\CC^1$ sur $]0,\infty[^2$, donc si $f$ admet un minimum globale en $(x,y)$, celui-ci
annule les dérivées partielles de $f$, soit:
$$\left\{
\begin{array}{ccc}
\dfrac{-a}{x^2}+\dfrac{y}{a^2}&=&0\\
&&\\
\dfrac{-a}{y^2}+\dfrac{x}{a^2}&=&0
\end{array}\right.
\Longleftrightarrow
\left\{
\begin{array}{ccc}
xy&=&\dfrac{a^3}{x}\\
&&\\
xy&=&\dfrac{a^3}{y}
\end{array}\right.\Longleftrightarrow x=y=a.
$$
Donc la valeur minimale de $f$, si elle existe, est atteinte en $(a,a)$ et vaut $f(a,a)=3$.
D'autre part,
- [$\diamondsuit$] Si $x\leq \dfrac{a}{3}$ alors $\dfrac{a}{x}\geq 3$ donc $f(x,y)\geq 3$.
- [$\diamondsuit$] Si $y\leq \dfrac{a}{3}$ alors $\dfrac{a}{y}\geq 3$ donc $f(x,y)\geq 3$.
- [$\diamondsuit$] Si $x\geq 9a$ et $y\geq \dfrac{a}{3}$ alors $\dfrac{xy}{a^2}\geq 3$ donc $f(x,y)\geq 3$.
- [$\diamondsuit$] Si $y\geq 9a$ et $x\geq \dfrac{a}{3}$ alors $\dfrac{xy}{a^2}\geq 3$ donc $f(x,y)\geq 3$.
On en déduit $\underset{(x,y)\in \R_+^2}{\inf}\,f=\underset{K}{\inf}\,f$ avec
$K=\left[\frac{a}{3},9a\right]$.
Comme $f$ est continue sur le compact $K$, alors $f$ atteint sa borne inférieure, et d'après ce qui
précède ce ne peut être qu'en $(a,a)$. D'où $\boxed{\min \,f=f(a,a)=3}$.
Déterminer les extremums (éventuels) de la fonction $f$ définie sur $(\R_+^*)^3$ par: $~~~~f(x,y,z)=xyz-\ln(x+y+z)$. Est-elle majorée? minorée?
$f$ est de classe $\CC^1$ sur $(\R_+^*)^3$, et on a
$$\dfrac{\partial f}{\partial x}(x,y,z)=yz-\dfrac{1}{x+y+z},$$
d'autre part, vu que $f(y,x,z)=f(z,y,x)=f(x,y,z)$, on en déduit alors
$$\dfrac{\partial f}{\partial y}(x,y,z)=xz-\dfrac{1}{x+y+z},\quad \dfrac{\partial f}{\partial
z}(x,y,z)=yx-\dfrac{1}{x+y+z}.$$
Ainsi $(x,y,z)$ est un point critique de $f$ ssi
$$yz-\dfrac{1}{x+y+z}=xz-\dfrac{1}{x+y+z}=xy-\dfrac{1}{x+y+z}=0$$
ce qui donne $x=y=z$ puis $x=y=z=1/\sqrt[3]{3}=\alpha$ (donc $\alpha^2=1/(3\alpha)$).
Pour connaître la nature de ce point, on pose $X=(u,v,w)$ et on étudie:
$$
\begin{array}{ll}
f(\alpha+u,\alpha+v,\alpha+w)-f(\alpha,\alpha,\alpha)&=
(\alpha+u)(\alpha+v)(\alpha+w)-\ln(3\alpha+u+v+w)-\alpha^3+\ln(3\alpha)\\
&=
(u+v+w)\alpha^2+(uv+uw+vw)\alpha+uvw -\ln(1+\frac{u+v+w}{3\alpha})\\
&=(u+v+w)\alpha^2+(uv+uw+vw)\alpha -\dfrac{u+v+w}{3\alpha}+\dfrac{(u+v+w)^2}{18\alpha^2}+o(\norme{X}^2)\\
&=(uv+uw+vw)\alpha +\dfrac{u^2+v^2+w^2+2uv+2uw+2vw}{18\alpha^2}+o(\norme{X}^2)\\
&=\frac{\alpha}{6}\left(u^2+v^2+w^2+8uv+8uw+8vw\right)+o(\norme{X}^2)
\end{array}
$$
Si on pose $u=v=w$ assez proche de $0$, on trouve
$$
f(\alpha+v,\alpha+v,\alpha+v)-f(\alpha,\alpha,\alpha)= \alpha\dfrac{9}{2}v^2+o(v^2)>0$$
Si on pose $u=-8v$ et $w=v$, on trouve
$$f(\alpha-8v,\alpha+v,\alpha+v)-f(\alpha,\alpha,\alpha)= -9\alpha v^2+o(v^2)< 0$$
Donc $f$ n'admet pas d'extremums.
$f$ n'est pas majorée puisque $f(x,x,x)\tendvers{x}{\infty}\,\infty$, et $f$ n'est pas minoré puisque
$f(x,1/x,1)=1-\ln(x+1/x+1)\tendvers{x}{-\infty}-\infty.$
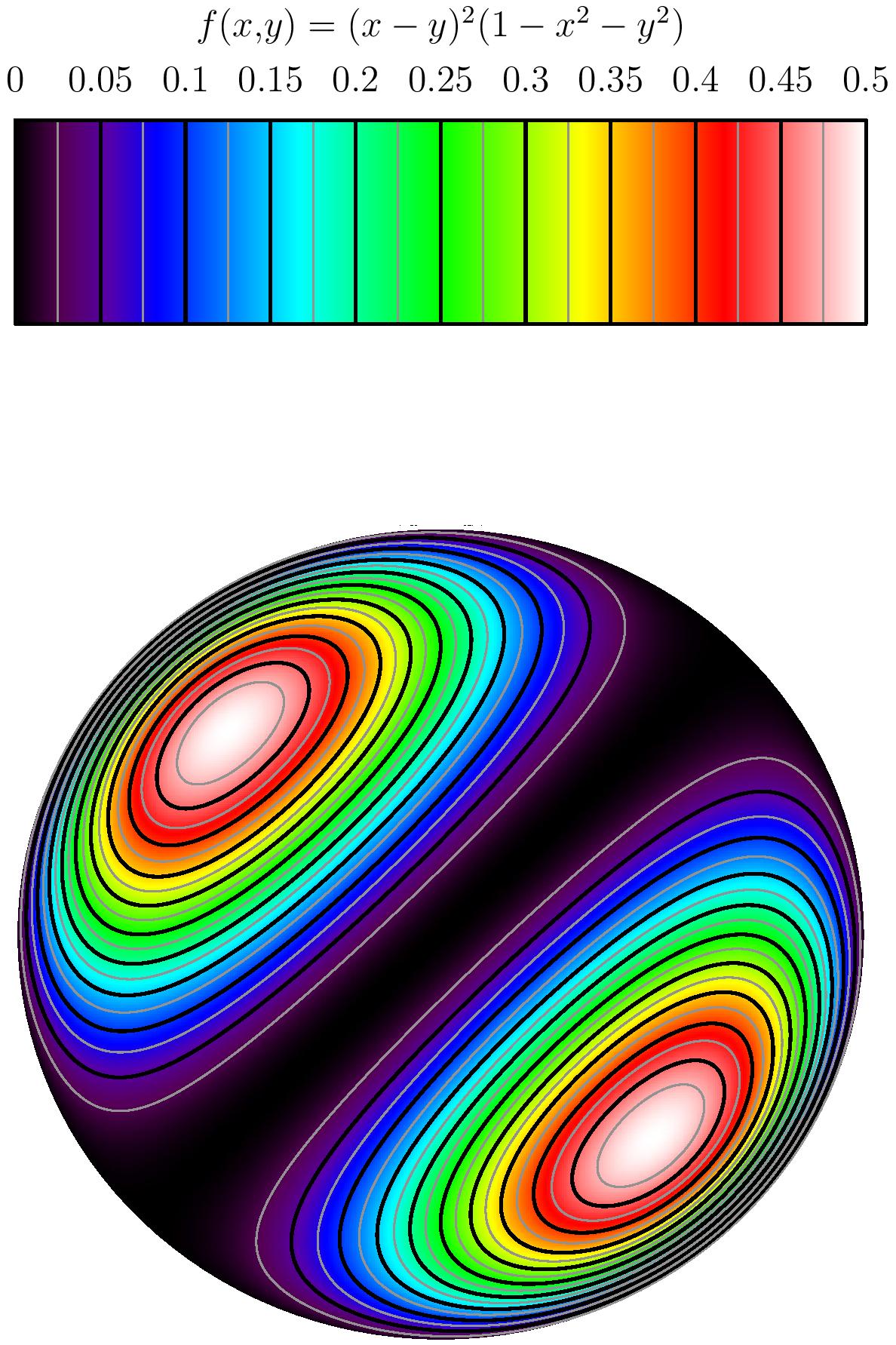
Posons $f(x,y)=(x-y)^2(1-x^2-y^2)$ pour $(x,y)\in\mathbb R^2$.
- Préciser le signe de $f$.
- Déterminer les points critiques de $f$.
- $f$ possède-t-elle un minimum global?
- Montrer que $f$ possède un maximum global et préciser les points où il est atteint.
- Préciser les extrema locaux de $f$.
-
On note $D$ la droite d'équation $y=x$, alors pour tout $(x,y)\in D$ on a $f(x,y)=0$, et pour tout
$(x,y)\in \R^2\setminus D,\,\,(x-y)^2>0$. Donc pour étudier le signe de $f$ il faut étudier le
signe de $1-x^2-y^2$.
Si $(x,y)\in \R^2\setminus D$ tel que $x^2+y^2< 1$ alors $f(x,y)>0$,
Si $(x,y)\in \R^2\setminus D$ tel que $x^2+y^2=1$ alors $f(x,y)=0$,
Si $(x,y)\in \R^2\setminus D$ tel que $x^2+y^2>1$ alors $f(x,y)< 0$. -
Le calculs des dérivées partielles de $f$ donne
$$\dfrac{\partial f}{\partial x}(x,y)=2(x-y)(-2x^2+yx-y^2+1),\,\,\dfrac{\partial f}{\partial
y}(x,y)=2(y-x)(-2y^2+yx-x^2+1).$$
Ainsi, $\dfrac{\partial f}{\partial x}(x,y)=\dfrac{\partial f}{\partial y}(x,y)=0$ ssi $x=y$ ou
$$x\neq y,\quad -2x^2+yx-y^2+1=-2y^2+yx-x^2+1=0$$
la résolution de la dernière relation donne $x=\frac{1}{2},y=\frac{-1}{2}$,
$x=\frac{-1}{2},y=\frac{1}{2}$.
Conclusion, les points critiques de $f$ sont, $$\{(x,y)\in \R^2,\,\, x=y\} \bigcup \left\{(\frac{1}{2},\frac{-1}{2}),\,(\frac{-1}{2},\frac{1}{2})\right\}.$$ -
Puisque $f(x,y)=f(- x,- y)$ il suffit alors d'étudier $f$ sur l'ensemble $\{(x,y)\in \R^2,\,x\geq
0\}$.
Comme $\dsp\lim_{x\to\infty}f(x,1)=-\infty$, on en déduit alors que $f$ n'admet pas un minimum global.
Si $f$ admet un maximum global, il sera parmi les points critiques de $f$.
Si $x=y$ alors $f(x,y)=0$ donc $(x,y)$ ne peut pas être un maximum (puisque $f>0$).
Donc seul possibilité $x=\frac{1}{2},\, y=\frac{-1}{2}$. On calcul alors
$$
\begin{array}{ll}
f(1/2+u,-1/2+v)-f(1/2,-1/2)&=(1-u+v)^2(1-(1/2+u)^2-(-1/2+v)^2)-1/2\\
&=(1+u-v)^2(1/2-u^2-v^2-u+v)-1/2\\
&=-\frac{5}{2}(u^2+v^2)+3uv +o(\norme{(u,v)}^2)
\end{array}
$$
On sait que $2uv\leq u^2+v^2$, donc
$$-\frac{5}{2}(u^2+v^2)+3uv \leq -\frac{5}{2}(u^2+v^2)+\frac{3}{2}(u^2+v^2)$$
soit
$$ -\frac{5}{2}(u^2+v^2)+3uv \leq-(u^2+v^2)\leq 0$$
on en déduit alors que pour $u,v$ assez proche de $0$,
$$f(1/2+u,-1/2+v)-f(1/2,-1/2)\leq 0$$
donc $f$ admet un maximum local au point $(1/2,-1/2)$ (et aussi au point $(-1/2,1/2)$).
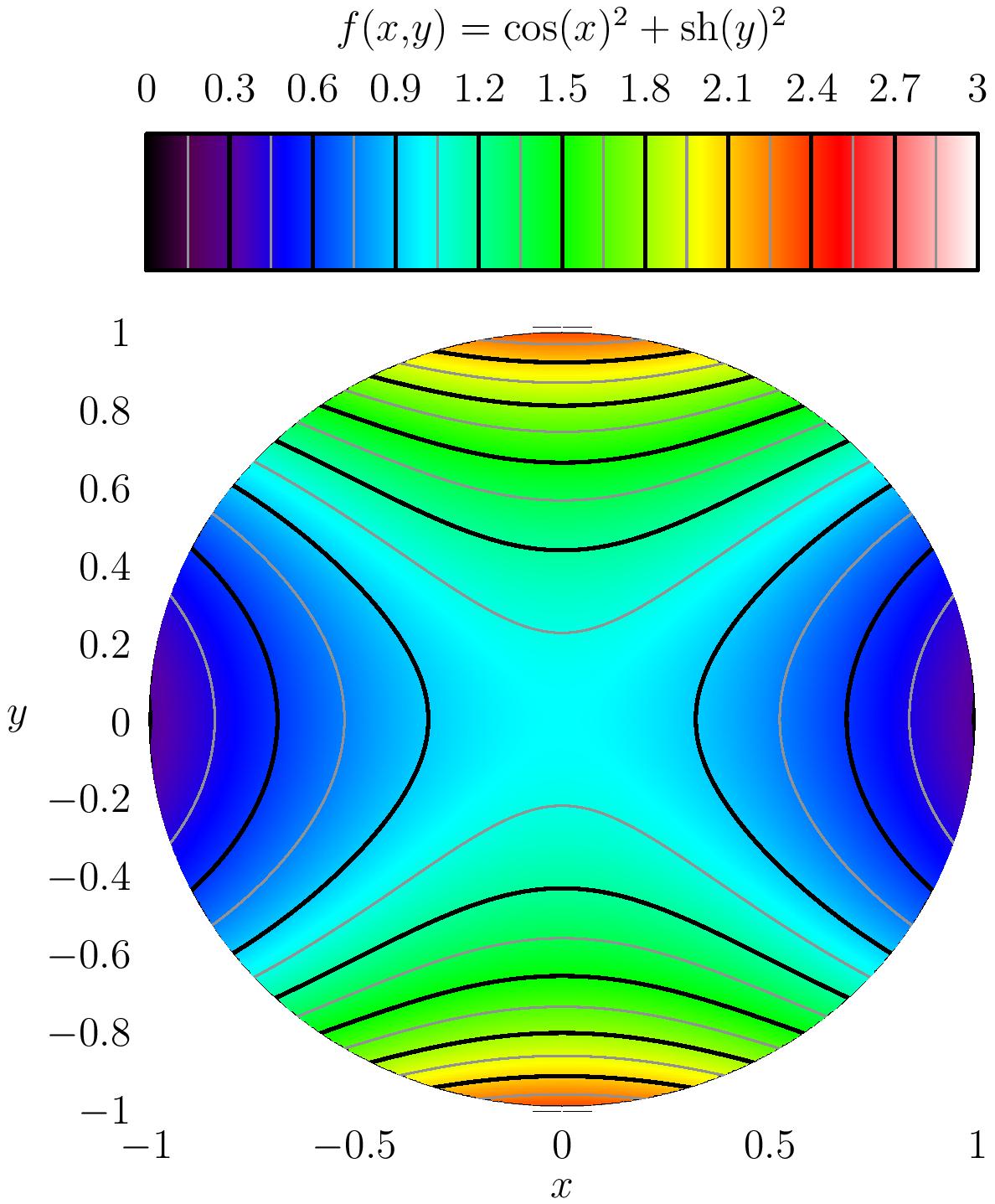
On note $D=\{z\in \mathbb{C} , |z|\leqslant 1\}$. Soit $f$ définie sur $D$ par: $\forall z \in D, f(z)=|\cos(z)|^2$.
- Montrer que $f$ est bornée sur $D$.
- Exprimer $f(z)$ en fonction de $\re(z)$ et de $\im (z)$. On rappelle que $\cos(z)=\frac1{2}(\ee^{\ii z}+\ee^{-\ii z})$.
- Déterminer le maximum et le minimum de $f$ sur $D$.
- La fonction $f$ est continue sur $D$ comme composées des fonctions continue, comme $D$ est un fermé borné de $\C$ et $f$ alors $f$ est bornée.
- On note $x=\re (z)$ et $y=\im (z)$, alors, $$ \begin{array}{lcl} \cos (z)&=& \dfrac{1}{2}\left(\ee^{\ii x-y}+\ee^{-\ii x+ y}\right)\\ &=& \dfrac{1}{2}\left(\ee^{- y}(\cos(x)+\ii \sin(x)+\ee^{y}(\cos(x)-\ii\sin(x))\right)\\ &=&\dfrac{1}{2}\left(\cos(x)\left(\ee^y+\ee^{-y}\right)+\ii \sin(x) \left(\ee^{-y}-\ee^y\right)\right)\\ &=&\cos(x)\ch(y)-\ii\sin(x)\sh(y) \end{array} $$ Donc, $$\forall z=x+\ii y\in D,\quad f(z)=\cos(x)^2\ch(y)^2+\sin(x)^2\sh(y)^2=\cos(x)^2+\sh(y)^2. $$
-
Cherchons les points critiques de $f$,
$$\dfrac{\partial f}{\partial x}(x,y)=\sin(2x),$$
$$\dfrac{\partial f}{\partial y}(x,y)=2\ch(y)\sh(y).$$
Donc $f$ admet $(0,0)$ comme point critique dans $D$.
Pour $u,v$ assez proche de $0$, on a $$f(u+\ii v) =1-\dfrac{u^2}{2}+v^2+\mathrm{o}(u^2+v^2).$$ On en déduit que $f$ n'admet pas un extremum en $(0,0)$.
Pour tout $z=x+\ii y\in D$, on a $\abs{x}\leq 1,\, \abs{y}\leq 1$ ce qui implique $ \cos(1)^2\leq \cos(x)^2\leq 1$, et $ 0\leq \sh^2(y)\leq \sh(1)^2.$
Donc $$\forall z\in D,\, \quad \cos(1)^2\leq f(z)\leq 1+\sh(1)^2.$$ Comme $f(1)=f(-1)=\cos(1)^2,\, f(-\ii)=f(\ii)=1+\sh(1)^2$, on en déduit que $\min f=\cos(1)^2,\,\max f=1+\sh(1)^2$.
Soit $\begin{array}{cccl}f: &\mathbb{R}^2&\to & \mathbb{R} \\& (x,y)&\mapsto & x^2+y^2-2x-4y\end{array}$.
- Déterminer les extremums de la fonction.
- $f$ admet-elle un maximum global sur $\mathbb{R}^2$ ?
- Préciser le minimum global sur $\mathbb{R}^2$.
-
Soit $D=\left \{ (x,y)\in\mathbb{R}^2,\, 0\leqslant x\leqslant 2\, ,\,0\leqslant y\leqslant x
\right \}$.
Représenter l'ensemble $D$. Quels sont les extremums globaux de $f$ sur $D$ ?
- On peut écrire $f$ sous la forme, $$\forall (x,y)\in \R^2,\quad f(x,y)=(x-1)^2+(y-2)^2-5.$$ Ainsi, $$\forall (x,y)\in \R^2,\,\,f(x,y)\geq -5 = f(1,2)\Longrightarrow \min_{\R^2} f=-5.$$ Donc $f$ admet un minimum globale atteint au point $(1,2)$.
- $f$ n'admet pas de maximum globale sur $\R^2$ puisque $\dsp\lim_{x\to \infty} f(x,0)=\infty.$
- $\min f= -5$.
-
Si $(x,y)\in D$ alors $0\leq x\leq 2$ et $0\leq y\leq x\leq 2$, donc
$$0-5\leq f(x,y)\leq 1^2+ 2^2 -5=0 =f(0,0)=f(2,0)$$
donc $f$ admet un maximum globale sur $D$, et il est atteint aux points $(0,0),\,(2,0)$.
Pour trouver le minimum de $f$ sur $D$ (on sait qu'il existe puisque $D$ est fermé borné et $f$ continue), c'est un peu plus compliqué!
Pour minimiser $f$ sur $D$ il faut que $x$ soit le plus proche à $1$ et $y$ le plus proche à $2$!
Puisque $0\leq y\leq x\leq 2$ alors $(2-y)^2\geq (2-x)^2$ et $-4x\leq -4y$, on en déduit alors $$\forall (x,y)\in D,\, f(x,y)\geq (x-1)^2+(x-2)^2-5=2x^2-6x\geq -4.5$$ d'autre par, $f(2/3,2/3)=-9/2$ donc $\dsp\min_D f=-9/2$.
On définit $f:(x,y)\mapsto x^3+y^3-3xy$. Étude des points critiques, puis des extremums éventuels.
$f$ est de classe $\CC^1$ sur $\R$, et on a
$$\dfrac{\partial f}{\partial x}(x,y)=3x^2-3y,\quad \dfrac{\partial f}{\partial y}(x,y)=3y^2-3x.$$
Un calcul simple nous donne
$$\dfrac{\partial f}{\partial x}(x,y)=\dfrac{\partial f}{\partial y}(x,y)=0\Longleftrightarrow (x,y)\in
\{(0,0),(1,1)\}.$$
Soit $h>0$ assez proche de $0$, on a
$$f(h,-h)=3h^2>f(0,0),\quad f(-h,-h)=-2h^3-3h^2< f(0,0).$$
On en déduit alors que le point $(0,0)$ n'est pas un extremum.
Soient $u,v\in \R$ assez proche de $0$, on a $$ \begin{array}{ll} f(1+u,1+v)-f(1,1)&=(1+u)^3+(1+v)^3-3(1+u)(1+v)+1\\ &= 3(u^2-uv+v^2)+u^3+v^3=3\left(\left(u-v/2\right)^2+\dfrac{3v^2}{4}\right)+u^3+v^3>0. \end{array} $$
On en déduit que $(1,1)$ est un extremum local (minimum locale) de $f$.
Par ailleurs, $f$ n'admet pas de minimum (ou maximum) globale puisque $\dsp\lim_{x\to \mp\infty}
f(x,1)=\mp \infty$.
- Soit $g:\R^*_-\longrightarrow \R, x\longrightarrow x\exp(\frac{1}{x})+\exp(x)$. Montrer que $g$ est croissante et calculer $g(-1)$.
- Soit $f:\R^2\longrightarrow\R, (x,y)\longrightarrow x\exp(y)+y\exp(x)$. Montrer que si $(x_0,y_0)$ est un point critique, alors $x_0< 0$ et $x_0y_0=1$ et $g(x_0)=0$. Déterminer le(s) point(s) critique(s).
- Soit $x\longrightarrow f(-1+ax,-1+x)$ où $a\in\R$. Donner un développement limité en 0 à l'ordre 2.
- Montrer que $f$ n'admet pas d'extremum local.
- Notons $D=\{(x,y)\in\mathbb R^2 / \mid x\mid\leq 1\ \text{et } \mid y\mid\leq 1\}$. Déterminer le minimum et le maximum de $f$ sur $D$ en justifiant leur existence.
- Pour tout $x< 0$, on a $$g'(x)=\ee^{\frac{1}{x}}-\frac{1}{x}\ee^{\frac{1}{x}}+\ee^x >0,$$ ce qui implique que $g$ est strictement croissante sur $\R_-^*$, et on a $g(-1)=-\ee^{-1}+\ee^{-1}=0$.
- Le calculs des dérivées partielles de $f$ donne: $$\dfrac{\partial f}{\partial x}(x,y)= \ee^y+y\ee^x,\,\, \dfrac{\partial f}{\partial y}(x,y)=x\ee^y+\ee^x.$$ Ainsi $(x_0,y_0)$ est un point critique ssi $$\left\{ \begin{array}{ll} \ee^{y_0}+y_0\ee^{x_0}&=0\\ x_0\ee^{y_0}+\ee^{x_0}&=0 \end{array} \right. \Longrightarrow \left\{\begin{array}{ll} \ee^{y_0}&=-y_0\ee^{x_0}\\ -x_0y_0\ee^{x_0}&=-\ee^{x_0} \end{array} \right. \Longrightarrow \left\{\begin{array}{l} y_0< 0 \quad (\ee^{x_0}>0,\,\ee^{y_0}>0)\\ x_0y_0=1 \quad (\ee^{x_0}>0) \end{array} \right. $$ Comme $y_0< 0$ alors $x_0< 0$, ainsi on obtient $$ 0= x_0\ee^{y_0}+\ee^{x_0} =x_0\ee^{-1/x_0}+\ee^{x_0}=g(x_0)$$ d'après la question précédente, le seule candidat est $x_0=-1$ ce qui implique $y_0=-1$, puis on vérifie facilement que le point $(-1,-1)$ est un point critique de $f$.
- Soit $a\in \R$, on pose $\varphi(x)= f(-1+ax,-1+x)$, pour $x$ au voisinage de $0$, on a $$ \begin{array}{lcl} \varphi(x)&=& \ee^{-1} \left((-1+ax)\ee^x+(-1+x)\ee^{ax}\right)\\ &=&\ee^{-1}\left((-1+ax)(1+x+\frac{x^2}{2})+(-1+x)(1+ax+\frac{a^2x^2}{2})\right)+\mathrm{o}(x^2)\\ &=&\ee^{-1}\left(-1+(a-1)x+(a-1/2)x^2-1+(1-a)x+(a-a^2/2) x^2\right)+\mathrm{o}(x^2)\\ &=&\ee^{-1}\left(-2-(a^2-4a+1)\frac{x^2}{2}\right) +\mathrm{o}(x^2) \end{array} $$
-
D'après la question précédente, on a
$$f(-1+ax,-1+x)-f(-1,-1)=-\ee^{-1}\left((a^2-4a+1)\frac{x^2}{2}\right) +\mathrm{o}(x^2)$$
Pour $x$ assez proche de $0$ et $a=2$, on trouve $f(-1+2x,-1+x)-f(-1,-1)\leq 0$.
Pour $a=1$, on trouve $f(-1+x,-1+x)-f(-1,-1)\geq 0$.
On en déduit alors que le point $(-1,-1)$ n'est pas un extremum de $f$, donc $f$ n'admet pas d'extremums. -
$D$ est un fermé borné de $\R^2$, $f$ est continue donc $f$ est bornée sur $D$ et atteints ses
bornes sur $D$.
D'autre part, il est claire que, $$\forall (x,y)\in D,\quad -2\ee^{-2}=f(-1,-1)\leq f(x,y)\leq f(1,1)=2\ee.$$ Ainsi, $\min_D f=-2\ee^{-1}$ et $\max_D f=2\ee$.
| $\,$ | ||
| $\,$ | $\,$ | $\,$ |
| $\,$ | ||
| $\,$ | $\,$ | $\,$ |