Etude locale des fonctions
Applications linéaires continues
($\star$)
Correction
Soient $E$ et $F$ deux espace vectoriels normés. On suppose qu'une suite $(f_n )$ d'éléments de
$\LL_\mathcal{C}(E,F)$ converge vers $f \in \LL_\mathcal{C}(E,F)$ (au sens de la norme subordonnée)
et qu'une suite $(x_n )$ d'éléments de $E$ converge vers $x \in E$. Établir que $f_n (x_n )
\tendversN f(x)$.
Correction
Notons $N$ la norme sur $\LL_\mathcal{C}(E,F)$, alors (rappelle de cours!)
$$\forall f\in \LL_\mathcal{C}(E,F),\,\,\forall x\in E,\quad \norme{f(x)}_F\leq N(f)\norme{x}_E.$$
Soit $(f_n)$ une suite d'éléments de $\LL_\mathcal{C}(E,F)$ qui converge vers $f\in
\LL_\mathcal{C}(E,F)$ et $(x_n)$ une suite d'éléments de $E$ qui converge vers $x$. Alors pour tout
$x\in E$, on a
$$\begin{array}{lcl}
\norme{f(x)-f_n(x_n)}&=& \norme{f(x)-f(x_n)+f(x_n)-f_n(x_n)}\\
&&\\
&\leq &\norme{f(x)-f(x_n)}+\norme{f(x_n)-f_n(x_n)}=\norme{f(x-x_n)}+\norme{(f-f_n)(x_n)}\\
&&\\
&\leq& N(f)\norme{x-x_n}_E+N(f-f_n)\norme{x_n}\tendversN\,0
\end{array}$$
La suite $(x_n)$ étant convergent donc bornée, donc $N(f-f_n)\norme{x_n}\tendversN\,0$, de même
$N(f)\norme{x-x_n}_E\tendversN\,0$.
On en déduit finalement que $f_n(x_n)\tendversN\,f(x)$.
($\star\star$)
Correction
Soient $E$ et $F$ deux espaces vectoriels normés et $f \in \LL(E,F)$. On suppose que, pour toute
suite $(u_n )$ tendant vers $0$, $f(u_n )$ est bornée. Montrer que $f$ est continue.
Correction
Supposons que $f$ n'est pas continue, alors
$$\forall n\in \N^*,\, \exists x_n \in E\setminus\{0\},\,\, \norme{f(x_n)}_F\geq n\norme{x_n}_E.$$
On pose alors $z_n=\dfrac{x_n}{\sqrt{n}\norme{x_n}_E}$, on a $\norme{z_n}=\dfrac{1}{\sqrt{n}}$ donc
$z_n\tendversN\,0$.
D'autre part, on a
$$\norme{f(z_n)}_F=
\norme{f\left(\dfrac{x_n}{\sqrt{n}\norme{x_n}_E}\right)}_F=\dfrac{1}{\sqrt{n}\norme{x_n}_E}\norme{f(x_n)}_F\geq
\dfrac{n\norme{x_n}_E}{\sqrt{n}\norme{x_n}_E}=\sqrt{n}\tendversN\,\infty$$
ce qui contredit l'hypothèse. Donc $f$ est continue.
(CCP )
Correction
Soient $E$ un espace vectoriel normé non réduit à $\left\{ 0 \right\}$ et $u,v \in \LL(E)$ continus
tels que
$$u \circ v - v \circ u = \alpha \mathrm{Id}e $$ pour un certain $\alpha \in \mathbb{R}$.
-
Établir que pour tout $n \in \N$, $u \circ v^{n + 1} - v^{n + 1} \circ u = (n + 1)\alpha
v^n$.
-
En déduire que $\alpha = 0$.
Correction
-
Par récurrence sur $n\in \N$, la relation est vraie pour $n=0$.
Soit $n\geq 0$ et supposons que la relation est vraie au rang $n$ i.e. $u \circ v^{n +1} -
v^{n +1} \circ u = (n+1) \alpha v^{n}$.
$$\begin{array}{lcl}
u \circ v^{n + 2} - v^{n + 2} \circ u& =&(u \circ v^{n+1})\circ v - v^{n+1} \circ (v \circ
u)\\
&=& ((n+1)\alpha v^{n} +v^{n+1}\circ u)\circ v- v^{n+1}(u\circ v-\alpha\mathrm{Id}e)\\
&=&(n+1)\alpha v^{n+1}+v^n\circ u\circ v-v^{n+1}\circ u\circ v+\alpha v^{n+1}=(n+2)v^{n+1}
\end{array}$$
Ceci montre que la relation est vraie au rang $n+1$.
-
Notons $\Norme{\phantom{f}}$ la norme subordonné sur $\LL_\mathcal{C}(E,F)$, (rappel..
$$\forall f\in \LL_\mathcal{C}(E,F),\quad \forall x\in E,\quad\norme{f(x)}_F\leq
\Norme{f}\,\norme{x}_E.$$
La relation précédente, implique que, pour tout $n\in \N$,
$$ \abs{\alpha}(n+1)\Norme{v^{n}}=\Norme{u \circ v^{n + 1} - v^{n + 1} \circ u }\leq
\Norme{u\circ v\circ v^n}+\Norme{v^n\circ v\circ u}\leq \left(\Norme{u\circ v}+\Norme{v\circ
u}\right) \Norme{v^{n}}$$
Ceci implique que $\abs{\alpha}\Norme{v^{n}}=0$ (il suffit de prendre $n\geq
\left(\Norme{u\circ v}+\Norme{v\circ u}\right)$ dans la dernière relation), donc soit
$\alpha=0$ ou $v^n=0$.
Si on suppose que $v^n=0$, alors en utilisant la relation de récurrence (au rang $n-1$) on
trouve que $v^{n-1}=0$ en répétant la même démarche, on trouve que $v=0$, ce qui donne
$\alpha\mathrm{Id}e =0$ donc $\alpha=0$.
Dans les deux cas, on trouve $\alpha=0$ CQFD.
($\star\star$)
Correction
On munit $\R[X]$ de la norme $\norme{\cdot}_{\infty}$. Étudier la continuité des applications
linéaires :
$$f_0:P \mapsto P(x_0) \ (x_0\in \R),\quad \qquad f_1:P \mapsto P',\quad \qquad f_2:P \mapsto
(X-1)P.$$
Lorsqu'elles sont continues, calculer leur norme.
Rappel: Si $P=\dsum_{k=0}^na_kX^k$, alors $\norme{P}=\dsp\max_{k\in \inter{0,n}}(|a_k|)$.
Correction
-
$f(P)=P(x_0)$.
Soit $P=\dsum_{k=0}^n a_kX^k\in \R[X]$ avec $n=\deg (P)$, alors
$$\abs{f(P)}=\abs{P(x_0)}=\abs{\dsum_{k=0}^n a_kx_0^k}\leq
\dsum_{k=0}^n\abs{a_k}\abs{x_0}^k\leq \norme{P}_\infty
\dsum_{k=0}^n\abs{x_0}^k=\norme{P}_\infty \dfrac{1-\abs{x_0}^{n+1}}{1-\abs{x_0}}.$$
Alors, on distingue deux cas,
- Si $x_0\in ]-1,1[$ alors $f$ est continue, et $\Norme{f}\leq
\dfrac{1}{1-\abs{x_0}}$, d'autre part, en posant pour $n\in \N$, $P=\dsum_{k=0}^n X^k $
(si $x_0\in [0,1[$) ou
$P=\dsum_{k=0}^n(-1)^kX^k$ si $x\in ]-1,0[$, on trouve
$$f(P)=\dsum_{k=0}^n\abs{x_0}^k=\dfrac{1-\abs{x_0}^{n+1}}{1-\abs{x_0}}\leq
\Norme{f}\norme{P}=\Norme{f} \Longrightarrow \Norme{f}\geq
\dfrac{1-\abs{x_0}^{n+1}}{1-\abs{x_0}}.$$
On en déduit alors que $\Norme{f}=\dfrac{1}{1-\abs{x_0}}$.
- Si $\abs{x_0}\geq 1$ alors $f$ n'est pas continue.
-
$f(P)=P'$.
On pose, pour $n\in \N^*$, $P_n=X^n$, alors $\norme{P_n}=1$ et
$\norme{f(P_n)}=\norme{nX^{n-1}}=n$, comme
$\dfrac{\norme{f(P_n)}}{\norme{P}}\tendversN\,\infty$, alors $f$ n'est pas continue.
-
$f(P)=(X-1)P$.
Soit $P=\dsum_{k=0}^na_kX^k$, alors
$$f(P)=\dsum_{k=0}^na_kX^{k+1}-\dsum_{k=0}^n
a_kX^k=-a_0+\dsum_{k=1}^n(a_{k-1}-a_k)X^k+a_nX^{n+1}\Longrightarrow \norme{f(P)}\leq
2\norme{P}$$
on en déduit que $f$ est continue et $\Norme{f}\leq 2$.
D'autre part, $f(1-X)=(X-1)(1-X)=-1+2X-X^2$, donc $\norme{f(1-X)}=2=2\norme{1-X}$ ce qui
implique que $\Norme{f}=2$.
($\star\star$)
Correction
Soit $E$ un $\R$ e.v.n, et $\varphi$ une forme linéaire non nulle sur $E$. Soit
$H=\Ker (\varphi)$.
-
Montrer que $\varphi$ est continue si et seulement si $H$ est fermé dans $E$.
-
On suppose $H$ fermé. Montrer que, pour tout $a \notin H \ , \ \|\varphi\|= \dsp
\frac{|\varphi(a)|}
{\ud (a,H)}$.
Correction
-
Puisque $\Ker (\varphi)=\varphi^{-1}(\{0\})$, donc si $\varphi$ est continue alors $\Ker
(\varphi)$ est un fermé de $E$
(image réciproque d'un fermé par une application continue).
Inversement, supposons que $H$ est un fermé de $E$, et montrons que $\varphi$ est
continue.
Supposons que $\varphi$ n'est pas continue, ce qui implique que $\varphi$ n'est pas bornée
sur la boule unité,
donc il existe une suite $(x_n)$ d'éléments de $B(0,1)$ tel que $\abs{\varphi(x_n)}$ tend
vers $\infty$ lorsque $n$ tend vers $\infty$. En particulier,
$$\exists N\geq 0,\, \forall n\geq N,\, \abs{\varphi(x_n)}>1\Longrightarrow\forall n\geq N,\,
x_n\not\in H.$$
On définit alors la suite $z_n=\dfrac{\varphi(x_N)}{\varphi(x_n)}x_n-x_N$ (pour $n\geq N$),
on vérifie
facilement que $z_n\in H$, de plus $z_n\tendversN -x_N$, comme $H$ est fermé alors $x_N\in H$
ce qui est absurde!
On en déduit alors que $\varphi$ est continue.
-
Soit $a\not\in H$, alors
$$\forall y\in H,\quad f(a)=f(a-y)\Longrightarrow \forall y\in
H,\,\abs{f(a)}=\abs{f(a-y)}\leq \norme{f}\norme{a-y}\Longrightarrow \abs{f(a)}\leq
\norme{f}\ud(a,H).$$
Ce qui donne $\dfrac{\abs{\varphi(a)}}{\ud (a,H)}\leq \norme{f}$.
D'autre part, pour tout $y\in E\setminus H$, on a
$$f\left(a-\frac{f(a)}{f(y)}y\right)=0\Longrightarrow a-\frac{f(a)}{f(y)}y\in H.$$
On obtient alors,
$$\norme{\frac{f(a)}{f(y)}y}=\norme{a-(a-\frac{f(a)}{f(y)}y)}\geq \ud (a,H)$$
ce qui donne, $\abs{f(y)}\leq \dfrac{\abs{f(a)}}{\ud (a,H)}\norme{y}$, cette dernière
relation reste vraie si $y\in H$, ainsi on a montré
$$\forall y\in E, \abs{f(y)}\leq \dfrac{\abs{f(a)}}{\ud (a,H)}\norme{y}\Longrightarrow
\norme{f}\leq \dfrac{\abs{f(a)}}{\ud (a,H)}$$
($\star\star$)
Correction
Soit $E = \CC(\left[ {0,1} \right],\mathbb{R})$ muni de $\left\| {\,.\,} \right\|_\infty $.
-
Montrer que pour toute fonction $f \in E$, il existe une unique primitive $F$ de $f$
vérifiant $\dsp\int_0^1 {F(t)\,{\mathrm{d}}t} = 0$.
-
Établir que l'application $u:f \mapsto F$ est un endomorphisme continu.
-
Justifier $\dsp F(x) = \int_0^1 {\left( {\int_t^x {f(u)\,{\mathrm{d}}u} }
\right)\,{\mathrm{d}}t} $.
-
Calculer $\left\| u \right\|$.
Correction
-
Pour l'unicité: Si $F_1,\,F_2$ sont deux primitives de $f$ alors il existe $\alpha\in \R$ tel
que $F_1=F_2+\alpha$, donc
$0=\dsp\int_0^1F_1=\dsp\int_0^1(F_2+\alpha)=\alpha$ ce qui donne $F_1=F_2$.
Pour l'existence: On pose $F(x)=\dsp\int_0^xf(t)\ud t -\int_0^1\left(\int_0^xf(u)\ud
u\right)\ud x$. Alors $F'=f$ et $\dsp\int_0^1F=0$ donc $F$ est une fonction qui convient.
-
Il est clair que $u\in \mathscr{L}(E)$, pour montrer que $u$ est continue il suffit de
montrer que
$$\exists k>0,\,\forall f\in E,\quad \norme{u(f)}_\infty\leq \norme{f}_\infty,\quad
\text{i.e. }, \forall x\in [0,1],\quad \abs{F(x)}\leq k\abs{f(x)}.$$
Soit $f\in E$, on a,
$$\begin{array}{lcl}
\forall x\in [0,1],\quad \abs{u(f)(x)}&=&\dsp \abs{\int_0^xf(u)\ud u -
\int_0^1\left(\int_0^uf(t)\ud t\right)\ud u}\\
&\leq &\dsp \norme{f}_\infty x+\int_0^1\norme{f}_\infty u\ud u \leq
\dfrac{3}{2}\norme{f}_\infty\\
&&\Longrightarrow\norme{u(f)}_\infty\leq \dfrac{3}{2}\norme{f}_\infty.
\end{array}$$
Ceci prouve la continuité de $u$.
-
Soient $f\in E,\,\,t,x\in [0,1]$, on a $\dsp\int_t^xf(u)\ud u=F(x)-F(t)$, donc
$$ \int_0^1\left( \int_t^x f(u)\,\ud u \right)\,\ud t=\int_0^1(F(x)-F(t))\ud
t=F(x)\int_0^1\ud t -\int_0^1F(t)\ud t=F(x).$$
-
Soit $f\in E$, en utilisant la relation précédente, on a pour tout $x\in [0,1]$
$$\begin{array}{lcl}
\abs{u(f)(x)}&=&\dsp \abs{\int_0^1\left( \int_t^x f(u)\,\ud u
\right)\,\ud t}\\
&&\\
&\leq &\dsp \int_0^1\abs{\int_t^xf(u)\ud u}\ud t\leq \int_0^1\norme{f}_\infty\abs{x-t}\ud t\\
&&\\
&=&\dsp \norme{f}_\infty\left(\int_0^x(x-t)\ud t+\int_x^1(t-x)\ud t\right)\\
&&\\
&=&\dsp \norme{f}_\infty\left(\frac{x^2}{2}+\frac{(1-x)^2}{2}\right)\leq
\frac{\norme{f}_\infty}{2}\Longrightarrow \norme{u(f)}_\infty\leq
\dfrac{1}{2}\norme{f}_\infty.
\end{array}$$
On en déduit que $\norme{u}\leq \frac{1}{2}$. D'autre part, en prenant $f=1$ on trouve que
$u(f)(x)=x-\frac{1}{2}$ ce qui donne $\norme{u(f)}_\infty=\frac{1}{2}\norme{f}_\infty$ donc
$\norme{u}\geq \frac{1}{2}$.
Conclusion, $\norme{u}=\dfrac{1}{2}$.
($\star\star$)
Correction
Soit $E$ un $\K$-espace vectoriel de dimension finie. Montrer que toutes les normes sur $E$ sont
équivalents.
Correction
Soient $N_1,\,N_2$ deux normes définies sur $E$. Puisque $E$ est de dimension finie, alors
$\mathrm{Id}e$ est continue de $(E,N_1)$ dans $(E,N_2)$, donc,
\begin{equation}
%\label{Eq22-1}
\exists K_1>0,\quad \forall x\in E,\, N_1(\mathrm{Id}e (x))=N_1(x)\leq K_1 N_2(x).\quad\quad (Eq-1)
\end{equation}
De même $\mathrm{Id}e$ est continue de $(E,N_2)$ dans $(E,N_1)$, donc,
\begin{equation}
% \label{Eq22-2}
\exists K_2>0,\quad \forall x\in E,\, N_2(\mathrm{Id}e (x))=N_2(x)\leq K_2 N_1(x). \quad\quad (Eq-2)
\end{equation}
Les relations (Eq-1) et (Eq-2) impliquent que les deux normes $N_1$ et $N_2$ sont
équivalentes.
($\star\star$)
Correction
Soit $E=\R_n[X]$ muni de la norme suivante $\norme{P}=\sup\{\abs{P(t)},\,t\in [0,1]\}.$
Montrer la relation suivante:
$$\exists c>0,\quad \forall P\in E,\, \abs{P(2019)+P(2020)} \leq c\int_0^1 \abs{P(t)}\ud t.$$
Correction
L'application $\fonct{\varphi}{E}{\R}{P}{P(2019)+P(2020)}$ est linéaire donc continue puisque $E$
est de dimension finie.
D'après la caractérisation des applications linéaires continues, il existe $K>0$, tel que pour tout
$P\in E$, on a
$\abs{\varphi(P)}\leq K\norme{P}$.
D'autre part, l'application qui à $P$ associé $\dsp\int_0^1\abs{P}$ définie une norme sur $E$ donc
équivalente à la norme déjà définie.
On en déduit alors
$$\exists \alpha>0,\quad \forall P\in E,\quad \norme{P}\leq \alpha \int_0^1\abs{P(t)}\ud t.$$
Il suffit alors de prendre $c=\alpha \times K$.
Continuité
E3A2018($\star$)
Correction
Soient $\Omega=\{\begin{pmatrix}
a&c\\b&d
\end{pmatrix}\in \MM_2(\R),\, (a-d)^2+4bc>0\}$ et $F=\{\begin{pmatrix}
a&c\\b&d
\end{pmatrix}\in \MM_2(\R),\, (a-d)^2+4bc\geq 0\}$.
Montrer que $\Omega$ est un ouvert de $\MM_2(\R)$ et $F$ est un fermé de $\MM_2(\R)$.
Correction
On définie la fonction $f$ de $\MM_2(\R)$ dans $\R$ par $f(A)= (a-d)^2+4bc$ si $A=\begin{pmatrix}
a&c\\b&d
\end{pmatrix}$. $f$ est une fonction polynomiale en les cordonnées de $A$ donc $f$ est continue sur
$\MM_2(\R)$.
Il suffit après d'écrire $\Omega=f^{-1}(\R_+^*)$ et $F=f^{-1}(\R_+)$.
($\star\star$)
Correction
-
Soit $f$ continue sur [0,1], à valeurs dans [0,1]. Montrer qu'il existe $c$ appartenant à
[0,1] tel que $f(c)=c$.
-
Soient $f$ et $g$, continues sur [0,1], à valeurs dans $[0,1]$, telles que $ f
\circ g = g \circ f$. Montrer qu'il existe $x$ appartenant à [0,1] tel que $f(x)=g(x)$.
Correction
-
On pose, pour $x\in [0,1],\,\,g(x)=f(x)-x$, alors $g\in \CC([0,1])$ de plus
$g(0)=f(0)\geq 1$ et $g(1)=f(1)-1\leq 0$ donc $g(1)g(0)\leq 0$, on en déduit d'après le TVI
qu'il existe $c\in [0,1]$ tel que $g(c)=0$ soit $f(c)=c$.
-
Supposons que, pour tout $x\in [0,1]$, $f(x)>g(x)$ alors il existe $\beta>0$ tel que $f\geq
\beta +g$. Ce qui donne:
$$\forall x\in [0,1],\,\,f^2(x)=f(f(x))\geq g(f(x))+\beta =f(g(x))+\beta\geq g(g(x))+2\beta
=g^2(x)+2\beta ,$$
puis on montre par récurrence sur $n\in \N^*$, que $f^n(x)\geq g^n(x)+n\beta$. Or $1\geq
f^n(x)-g^n(x)\geq n\beta$ ce qui est impossible.
De même en échangeant les rôles entre $f$ et $g$, on trouve que l'hypothèse $g>f$ est
impossible. On en déduit qu'il existe $c\in [0,1]$ tel que $f(c)=g(c)$.
($\star\star$)
Correction
Soit l'application $\fonct{G}{\R^2}{\R^2}{
(u,v)}{(\frac{u}{u+v},\frac{\sqrt{v(v+2u)}}{u+v})}$. On note
$\mathcal{D}$ l'ensemble de définition de $G$. Déterminer $G(\mathcal{D})$. $G$ est-elle continue sur $\mathcal{D}$?
Correction
Déterminons d'abord le domaine de définition de $f$. $f$ est définie pour $(u,v)\in \R^2$ tels que : $u+v\neq 0$ ET $v(v+2u)\geq 0$.
Soit $(u,v)\in \mathcal{D}$, on a:
$$ \left(\dfrac{u}{u+v}\right)^2 + \left(\dfrac{\sqrt{v(v+2u)}}{u+v}\right)^2=\dfrac{u^2+v(v+2u)}{(u+v)^2}=\dfrac{(u+v)^2}{(u+v)^2}=1.$$
On en déduit alors que $G(\mathcal{D})\subset \CC=\{(x,y)\in \R^2,\,x^2+y^2=1\}$.
Inversement, soit $(x,y)\in \CC$,
-
Si $x\neq 0$ et $xy\geq 0$, on pose
$$u =1,\, v=-1+\dfrac{1}{x},\,\, u+v=\dfrac{1}{x}\neq 0,\, v(v+2u)=(-1+\dfrac{1}{x})(1+\dfrac{1}{x})=-1+\dfrac{1}{x^2}=\dfrac{y^2}{x^2}>0$$
donc $(u,v)\in \mathcal{D}$, de plus;
$$F(u,v)=\left(\dfrac{1}{1-1+\dfrac{1}{x}}, \dfrac{\sqrt{(-1+\dfrac{1}{x})(1+\dfrac{1}{x})}}{1-1+\dfrac{1}{x}}\right) =
(x,x\dfrac{\abs{y}}{\abs{x}})=(x,x\dfrac{y}{x})=(x,y) $$
donc $(x,y)\in G(\mathcal{D})$
-
Si $x\neq 0$ et $xy\leq 0$, on pose
$$u =-1,\, v=1-\dfrac{1}{x},\,\, u+v=\dfrac{-1}{x}\neq 0,\, v(v+2u)=(1-\dfrac{1}{x})(-1-\dfrac{1}{x})=-1+\dfrac{1}{x^2}=\dfrac{y^2}{x^2}>0$$
donc $(u,v)\in \mathcal{D}$, et on vérifie que
$$F(u,v)=\left(\dfrac{-1}{1-1-\dfrac{1}{x}}, \dfrac{\sqrt{(-1-\dfrac{1}{x})(1-\dfrac{1}{x})}}{1-1+\dfrac{-1}{x}}\right)
=(x,-x\dfrac{\abs{y}}{\abs{x}})=(x,-x\dfrac{-y}{x})=(x,y) $$
donc $(x,y)\in G(\mathcal{D})$
-
Le cas $x=0,\, y=\mp 1$ ne pose aucun problème (puisque $(0,1)=G(0,1),\,(0,-1)=G(0,-1)$)
On en déduit alors que $G(\mathcal{D})=\CC$.
($\star$)
Correction
-
Soient $E$ est un espace vectoriel normé de dimension finie, $f : E \longmapsto \R$ une
application continue et $a\in \R$. Dire si les ensembles suivants sont ouverts ou
fermés :
$$A=\{x \in E\mid f (x) = a\}, B=\{x \in E \mid f (x) \leq a\},
C = \{x \in E \mid f (x) < a\}.$$
-
Montrer que $GL_n (\K)$ est ouvert dans $\MM_n (\K)$ .
-
Soit $f$ une fonction continue de $\R$ dans $\R$. Montrer que son graphe
$G = \{(x, f (x)) \mid x \in \R\}$ est fermé dans $\R^2$.
Correction
-
$A=f^{-1}(\{a\})$ donc $A$ est un fermé, $B=f^{-1}(]-\infty,a])$ donc $B$ aussi est un fermé.
En revanche, $C=f^{-1}(]-\infty,a[)$ donc $C$ est un ensemble ouvert.
-
L'application $\fonct{\det}{\MM_n(\R)}{\R}{A}{\det(A)}$ est une fonction continue, puisqu'il
s'agit d'une
fonction polynomiale en les coordonnées de $A$ (mais aussi une application $n$-linéaire donc
continue).
On sait que $GL_n(\R)=\det^{-1}(\R^*)$ donc $GL_n(\R)$ est un ensemble ouvert.
-
On définit sur $\R^2$ la fonction $\varphi$ par $\varphi (x,y)=y-f(x)$. $\varphi$ est
continue sur $\R^2$ comme la somme de deux fonctions continues, et on a
$G=\varphi^{-1}(\{0\})$ donc $G$ est un fermé de $\R^2$.
Remarque: On aurait pu aussi utiliser la caractérisation séquentielle de la continuité.
En effet, si $((x_n,y_n))_n$ une suite d'éléments de $G$ qui converge dans $\R^2$, alors $x_n\tendversN\, x$ puis
$y_n=f(x_n)$ (puisque $(x_n,y_n)\in G$) converge vers $f(x)$ puisque $f$ est continue.
Ainsi la limite de la suite $((x_n,y_n))_n$ est dans $G$ ce qui prouve que $G$ est un fermé.
($\star\star$)
Correction
Soient $E$ un espace vectoriel normé et $A$ une partie non vide de $E$. Pour $x \in E$, on pose
$$\ud(x,A) = \inf \left\{ \norme{x - a},\,\,a \in A \right\}$$
Montrer que l'application $x \mapsto \ud(x,A)$ est définie et continue sur $E$.
Correction
L'application $\ud$ est bien définie (c.f. cours). Soient $x,y\in E$, on a
$$\forall z\in A,~\ud(x,A)\leq \norme{x-z}\leq \norme{x-y}+\norme{y-z}$$
donc
$$\forall z\in A,~~\ud(x,A)- \norme{x-y}\leq \norme{y-z}\Longrightarrow \ud(x,A)- \norme{x-y}\leq
\ud(y,A)$$
En échangeant les rôles entre $x$ et $y$, on trouve
$$d(y,A)- \norme{y-x}\leq d(x,A)\Longrightarrow \boxed{\abs{\ud (x,A)-\ud (y,A)}\leq
\norme{x-y}}.$$
Donc l'application $\ud $ est $1$- lipschitzienne. On en déduit alors que $x \mapsto \ud(x,A)$ est
continue.
($\star\star$)
Correction
Soit $E$ un evn
-
Soient $A,\,B$ deux fermés non vides de $E$. Montrer que:
$$A\cap B =\emptyset \Longleftrightarrow \forall x\in E,\quad \ud (x,A)+\ud (x,B)\neq 0.$$
-
On suppose que $A\cap B=\emptyset$. Construire une application $f$ continue de $E$ dans $\R$
telle que $f_{\mid A}=0$ et $f_{\mid B}=1$.
En déduire l'existence de deux ouverts disjoints $U$ et $V$ tels que $A\subset U$ et
$B\subset V$.
Correction
-
On sait que $\ud (x,A)=0\Leftrightarrow x\in \overline{A}$, puisque $A$ et $B$ sont fermés
alors $\overline{A}=A$ et $\overline{B}=B$. Donc en utilisant la première remarque, on a:
$$\begin{array}{lcl}
\ud (x,A)+\ud (x,B)=0&\Longleftrightarrow & \ud (x,A)=0=\ud (x,B)\\
&\Longleftrightarrow & x\in A \text{ et }x\in B\\
& \Longleftrightarrow & x\in A\cap B
\end{array}$$
On en déduit donc, $A\cap B=\emptyset$ ssi pour tout $x\in E,\quad \ud (x,A)+\ud (x,B)>0$.
-
On définit $f$ par,
$$\forall x\in E,\,\,f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}.$$ $f$ est bien définie
puisque $\ud (x,B)+\ud (x,A)>0$. De plus $f$ est continue sur $E$, puisque $x\mapsto
\ud(x,A)$ (resp. $x\longmapsto \ud(x,B)$) sont continues sur $E$. D'autre part, on a:
$$\forall x\in A,\quad f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}=\dfrac{0}{\ud (x,B)}=0,$$
$$ \forall x\in B,\quad f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}=\dfrac{\ud (x,A)}{\ud
(x,A)}=1.$$
Posons maintenant $U=f^{-1}(]-\infty,\frac{1}{2}[),\,\, V=f^{-1}(]\frac{1}{2},\infty[)$, comme $f$
est continue on a $U,\,V$ sont des
ouverts de $E$ et clairement $U\cap V=\emptyset$ et $A\subset U,\,\,B\subset V$.
($\star\star$)
Correction
Soient $E$ un $\R$-evn de dimension finie et $F$ une partie bornée non vide de $E$.
On définie $\delta (F)=\underset{x,\,y\in F}{\sup}\norme{x-y}$.
-
Montrer que $\delta (F)$ est bien définie.
-
Peut-on avoir $\delta(F)=0$?
-
On suppose de plus que $F$ est fermé et $F$ n'est pas un singleton. Montrer qu'il existe $(x_0,y_0)\in F^2$ tel que $\delta (F)=\norme{x_0-y_0}$,
puis montrer que $x_0,\,y_0$ ne sont pas dans $\overset{\circ}{F}$.
Correction
-
Notons $A=\{\norme{x-y},\,x,y\in F\}\subset \R$, $A$ n'est pas vide car
$F\neq \emptyset$, de plus $A$ est borné, en effet comme $F$ est borné, alors
$$\exists M>0,\,\forall z\in F,\,\norme{z}\leq M\Longrightarrow \forall x,y\in F,\quad \norme{x-y}\leq \norme{x}+\norme{y}\leq 2M.$$
Ainsi, $A$ admet une borne supérieur, autrement dit, $\delta (F)$ est bien définie.
-
Si $F$ contient au moins 2 éléments $x\neq y$ alors
$\delta (F)>\norme{x-y}>0$.
Donc $\delta (F)=0$ ssi $F$ ne contient qu'un seul élément.
-
Considérons la fonction $\fonct{\varphi}{F\times F}{\R}{(x,y)}{\norme{x-y}}$.
$\varphi$ est continue sur $F^2$, de plus $F^2$ est un fermé borné de $E^2$,
donc d'après le cours $\varphi$ est borné sur $F^2$ et atteint ses bornes.
Ainsi, il existe $(x_0,y_0)\in F^2$ tel que $\varphi (x_0,y_0)=\dsp\sup_{F^2}\varphi=\delta (F)$.
Supposons que $x_0\in\overset{\circ}{F}$ alors il existe $r>0$ tel que $B(x_0,r)\subset F$.
On pose alors $z_0=x_0+\dfrac{r}{2}(x_0-y_0)$ de sorte que $z_0\in B(x_0,r)$ donc $z_0\in F$,
puis
$$\varphi(z_0,y_0)=\norme{x_0+\dfrac{r}{2}(x_0-y_0)-y_0}=\left(1+\dfrac{r}{2}\right)\norme{x_0-y_0}>\varphi(x_0,y_0)$$
ce qui est absurde, donc $x_0\not\in \overset{\circ}{F}$.
De même on montre que $y_0\not\in \overset{\circ}{F}$.
($\star\star$)
Correction
Soit $E$ un $\R$-espace vectoriel de dimension finie, $K$ un fermé borné de $E$ et $f:K\to K$
vérifiant :
$$
\forall x,y\in K,~~~~(x\not = y\Longrightarrow \norme{f(x)-f(y)}< \norme{x-y}).$$
-
Montrer que $f$ est continue sur $K$.
-
Montrer que $f$ admet un point fixe et un seul sur $K$. (On pourra considérer $g:K\to
\R,x\mapsto
\norme{f(x)-x}$.)
Correction
-
L'application $f$ est $1$- lipschitzienne donc $f$ est continue sur $K$.
-
On définit $\fonct{g}{K}{\R_+}{x}{\norme{f(x)-x}}$. La fonction $g$ est continue sur un fermé
bornée à valeur dans $\R_+$ donc elle atteint ses bornes (
cours), donc
$$\exists \ell\in K,\, g(\ell)=\norme{f(\ell)-\ell}=\underset{x\in K}{\min}(g(x)).$$
Montrons que $g(\ell)=0$ (ce qui donne $f(\ell)=\ell$). Pour cela, on va raisonner par
l'absurde, supposons que $g(\ell)>0$, alors d'après la définition de
$\ell$, on a
$$0< \norme{f(\ell)-\ell}=g(\ell)\leq g(f(\ell))=\norme{f(f(\ell))-f(\ell)}<
\norme{f(\ell)-\ell}\Longrightarrow \norme{f(\ell)-\ell}< \norme{f(\ell)-\ell},$$
ce qui est impossible donc $g(\ell)=0$ soit $\ell$ un point fixe de $f$.
Il reste à montrer l'unicité de $\ell$, supposons qu'il existe un autre point fixe $\ell'$ de
$f$ avec $\ell\neq \ell'$, alors
$$0< \norme{\ell-\ell'}=\norme{f(\ell)-f(\ell')}< \norme{\ell-\ell'} \Longrightarrow
\text{contradiction}.$$
Donc $\ell$ est le seul point fixe de $f$.
($\star$)
Correction
Soit $f$ la fonction définie sur $\R^2$ par:
$$\forall x\in \R^*,y\in \R,\quad f(x,y)=\dfrac{\sin(xy)}{x}, \text{ et }, \forall y\in \R,\quad f(0,y)=y.$$
Étudier la continuité de $f$.
Correction
On définit sur $\R$ la fonction $\varphi$ par,
$$\forall t\neq 0, \quad \varphi(t)=\dfrac{\sin(t)}{t},\text{ et } \varphi(0)=1.$$
Il est clair que $\varphi\in \CC(\R^*)$, de plus comme $\dfrac{\sin(t)}{t}\tendvers{t}{0}1$, on en déduit que $\varphi\in \CC(\R)$.
On remarque que, pour tout $(x,y)\in \R^2,\, f(x,y)=y\varphi(xy)$.
On en déduit alors que $f\in \CC(\R^2,\R)$ comme produit et composition des fonctions continues.
($\star\star$)
Correction
Soit $f\in \CC(\R)$. On définit la fonction $g$ sur $\R^*\times \R$ par:
$$\dsp\forall (x,y)\in \R^*\times \R,~~~~g(x,y)=\dfrac{1}{x}\int_x^{xy}f(t)\ud t.$$
Montrer que la fonction $g$ peut se prolonger par continuité sur $\R^2$.
Correction
Comme $f$ est continue sur $\R$, alors $f$ admet une primitive sur $\R$, qu'on note $F$ ($F\in
\CC^1(\R,\R)$ et $F'=f$).
On note aussi $\fonct{p_1}{\R^2}{\R}{(x,y)}{x}$ et $\fonct{p_2}{\R^2}{\R}{(x,y)}{y}$. Il est clair
que $p_1, p_2$ sont continues sur $D$,
de plus $p_1$ ne s'annule pas sur $D$ donc $1/p_1$ est aussi continue sur $D$.
On peut alors écrire $g=\dfrac{F\circ (p_1p_2)-F\circ p_1}{p_1}$, ceci prouve que $g$ est continue
sur $D$.
D'autre par, pour tout $x\neq 0$ et $y\neq 0$, on a
$$\begin{array}{lcl}
g(x,y)&=&\dfrac{F(yx)-F(x)}{x}=\dfrac{F(yx)-F(0)+F(0)-F(x)}{x-0}\\
&&\\
&=&y\dfrac{F(yx)-F(0)}{yx-0}-\dfrac{F(x)-F(0)}{x-0}\tendvers{x}{0}yF'(0)-F'(0)
\end{array}$$
Comme $F'(0)=f(0)$, alors $g(x,y)\tendvers{x}{0} (y-1)f(0)$. Ce résultat reste vrai si $y=0$
puisque
$$g(x,0)=\dfrac{-1}{x}\dsp\int_0^xf(t)\ud t\tendvers{x}{0}-f(0).$$
On en déduit qu'on peut prolonger $g$ par continuité sur $\R^2$, on posant
$g(0,y)=(y-1)f(0)$.
($\star-\star\star$)
Correction
Déterminer toutes les applications $f$ dans chacun des cas suivants:
-
$f:\R\to\R$, $f$ continue et $\forall x\in \R\ , \ f(2x+1)=f(x)$.
-
$f:\R\to\R$, $f$ continue et $\forall x,y\in \R\ , \ f(x+y)=f(x)+f(y)+xy$.
-
$f:\R_+^*\to\R$, $f$ continue et $\forall x,y\in \R_+^*\ , \ f(xy)=xf(y)+yf(x)$.
-
$f:\R\to\R$ , $f$ continue et $\forall x,y\in \R\ , \,
f\left(\dfrac{x+y}{2}\right)=\dfrac12\left(f(x)+f(y)\right)$.
Correction
-
Soit $x\in \R$, on a
$$\begin{array}{lcl}
f(x)&=&f\left(2\left(\frac{x}{2}-\frac{1}{2}\right)+1\right)=
f\left(\frac{x}{2}-\frac{1}{2}\right)\\
&&\\
&=&
f\left(2\left(\frac{x}{4}-\frac{1}{4}-\frac{1}{2}\right)+1\right)=f\left(\frac{x}{4}-\frac{1}{2}-\frac{1}{4}\right)\\
&&\\
&=&f\left(\frac{x}{4}-\frac{3}{4}\right).
\end{array}$$
Puis, on montre par récurrence sur $n\in \N$, que pour tout $n\in \N,\quad
f(x)=f\left(\frac{x}{2^n}-\frac{2^n-1}{2^n}\right)$. Comme $f$ est continue, et la suite
$\left(\frac{x}{2^n}-\frac{2^n-1}{2^n}\right)_{n\in \N}$ converge dans $\R$, alors
$$f(x)=\limiteX{n}{\infty}f\left(\frac{x}{2^n}-\frac{2^n-1}{2^n}\right)=f\left(\limiteX{n}{\infty}\left(\frac{x}{2^n}-\frac{2^n-1}{2^n}\right)\right)=f(-1)
,$$
car $\dsp \frac{x}{2^n}-\frac{2^n-1}{2^n}\tendversN -1$.
On en déduit alors que $f$ est une fonction constante.
Inversement, si $f$ est constante alors $f$ vérifie la condition $f(2x+1)=f(x)$.
-
Soit $f$ une fonction continue vérifiant la condition $f(x+y)=f(x)+f(y)+xy$. Alors, on a
$f(0)=2f(0)+0$ ce qui donne $f(0)=0$, puis
$$f(2)=f(1)+f(1)+1=2f(1)+1,\quad f(3)=f(2+1)=3f(1)+3,$$
$$f(4)=f(2+2)=4f(1)+7,\quad f(5)=f(3+2)=5f(1)+10,\cdots.$$
On montre alors que, pour tout $n\in \N,\quad f(n)=nf(1)+\dfrac{n(n-1)}{2}$ (démonstration
par récurrence).
Ensuite, pour $q\in \N^*$, on a
$$\begin{array}{lcl}
f(1)&=&f\left(\frac{q}{q}\right)=f\left(\frac{q-1}{q}+\frac{1}{q}\right)=f\left(\frac{q-1}{q}\right)+f\left(\frac{1}{q}\right)+\dfrac{q-1}{q^2}\\
&=&f\left(\frac{q-2}{q}\right)+f\left(\frac{1}{q}\right)+\dfrac{q-2}{q^2}+f\left(\frac{1}{q}\right)+\dfrac{q-1}{q^2}\\
&=&f\left(\frac{q-2}{q}\right)+2f\left(\frac{1}{q}\right)+\dfrac{q-2}{q^2}+\dfrac{q-1}{q^2}\\
&=&\cdots
=f(0)+qf\left(\frac{1}{q}\right)+\dfrac{1+2\cdots+(q-1)}{q^2}=qf\left(\frac{1}{q}\right)+\dfrac{q(q-1)}{2q^2}
\end{array}$$
Ce qui donne,
$f\left(\frac{1}{q}\right)=\frac{1}{q}f(1)+\frac{1}{2}\frac{1}{q}\left(\frac{1}{q}-1\right)$.
On montre après que pour tout $q\in \N^*$ et $p\in \N$,
$f\left(\frac{p}{q}\right)=pf\left(\frac{1}{q}\right)+\frac{p(p-1)}{2q^2}$.
On en déduit finalement que $f$ sur $\Q_+$ est de la forme $f(x)=xf(1)+\frac{x(x-1)}{2}$,
ensuite par densité de
$\Q_+$ dans $\R_+$ et vu que $f$ est continue, on trouve que $f$ est de la forme
$f(x)=\frac{x^2}{2}+\alpha x,\,\alpha\in \R$.
Pour $x\in \R_-$, on a $0=f(x-x)=f(x)+f(-x)-x^2$ donc $f(x)=x^2-f(-x)=\frac{x^2}{2}+\alpha
x$.
Inversement, si $f$ est définie par $f(x)=x^2/2+\alpha x$ on vérifie facilement que $f$ est
une solution de l'équation. On en déduit que l'ensemble de solution est
$\{f(x)=\frac{x^2}{2}+ax,\,\,a\in \R\}$.
-
On pose $g(z)=\frac{f(z)}{z}$, $g$ vérifie:
$$\forall x,y>0,\, g(xy)=g(x)+g(y),$$
comme $g$ est continue, on a $g(x)=k\ln(x)$ (avec $k\in \R$). On en déduit que
$f(x)=kx\ln(x)$.
-
Soit $f$ une fonction vérifiant la relation, alors $g=f-f(0)$ vérifie également la même
relation mais avec
$g(0)=0$.
Pour $x\in \R$, on a
$2g(x/2)=g(x)$ puis pour $x,y\in R$, on a
$g(\frac{x+y}{2})=\frac{1}{2}(g(x)+g(y))=g(x/2)+g(y/2)$.
Donc $g$ est de la forme $g(x)=\lambda x$ avec $\lambda\in \R$.
($\star\star$)
Correction
Soit $\varphi:\,(\MM_n(\R)\setminus\{0\})^2\mapsto\R$ définie par $\varphi(A,B)=\dfrac{\norme{AB}_1}{\norme{A}_1\norme{B}_1}$.
Montrer que $\varphi$ est continue, bornée puis trouver $\sup\varphi$.
Même question avec $g(A,B)=\dfrac{\norme{AB}_2}{\norme{A}_2\norme{B}_2}$ et
$h(A,B)=\dfrac{\norme{AB}_\infty}{\norme{A}_\infty\norme{B}_\infty}$.
Correction
L'application $\psi :(A,B)\in \MM_n(\R)^2\longmapsto AB $ est continue sur $\MM_n(\R)$ car $\psi$ est bilinéaire.
L'application $N:A\in \MM_n(\R)\setminus\{0\}\longmapsto \norme{A}_1$ est continue sur $\MM_n(\R)\setminus\{0\}$ (1-Lipschitzienne), de plus
ne s'annule pas sur $\MM_n(\R)\setminus\{0\}$.
L'application $\varphi$ est donc continue comme composé et produit des fonctions continues ($\varphi(A,B) =
N(\psi(A,B))/(N(A)\times N(B))$).
Soient $A=(a_{i\,j}), \, B=(b_{i\,j})$ deux matrices non nulles, on a
$$\forall (i,j)\in \inter{1,n}^2,\, (AB)_{i\,j}=c_{i\,j}=\dsum_{k=1}^n a_{i\,k}b_{k,j} \longrightarrow \abs{c_{i\,j}}\leq
\dsum_{k=1}^n \abs{a_{i\,k}}\abs{b_{k,j}}.$$
Notons, pour $i\in \inter{1,n},\, L_i(A)=\dsum_{k=1}^n\abs{a_{i\,k}}$,
On en déduit alors
$$\forall (i,j)\in \inter{1,n}^2,\, \abs{c_{i\,j}}\leq
L_i(A)\dsum_{k=1}^n \abs{b_{k,j}}$$
donc,
$$ \norme{AB}_1\leq \dsum_{i=1}^n \dsum_{j=1}^n\left(L_i(A) \dsum_{k=1}^n\abs{b_{k\,j}}\right)
= \dsum_{i=1}^n \left(L_i(A) \dsum_{j=1}^n\dsum_{k=1}^n\abs{b_{k\,j}}\right)=\norme{B}_1\dsum_i L_i(A)=\norme{B}_1\norme{A}_1.$$
Donc $\varphi(A,B)\leq 1$, ceci prouve que $\varphi$ est bornée et $\sup\varphi \leq 1$.
On pose $A=E_{1\,1}$ la matrice dont tous les coefficients sont nuls sauf $a_{1\,1}=1$, on a
$$A\neq 0,\,\,\norme{A}_1=1,\,\, A^2=A,\quad \varphi(A,A)=\dfrac{\norme{A^2}_1}{\norme{A}_1^2}=\dfrac{1}{1}=1 $$
donc $\sup\varphi \geq 1$. On en déduit alors que $\boxed{\sup\varphi =1 }$.
Pour la fonction $g$, soient $A=(a_{i\,j}), \, B=(b_{i\,j})$ deux matrices non nulles, on a
$$
\begin{array}{lcl}
\norme{AB}_2^2&=&\dsp \dsum_{1\leq i,j\leq n}\left(\dsum_{k=1}^n a_{i\,k}b_{k\,j}\right)^2\\
&&\\
&\leq & \dsp \dsum_{1\leq i,j\leq n}\left(\dsum_{\alpha =1}^n a_{i\,\alpha}^2\right)^2\left(\dsum_{\beta =1}^nb_{\beta \,j}^2\right)
\quad (\text{Cauchy-Schwarz})\\
&&\\
&=&\dsum_{1\leq i,j\leq n}\dsum_{1\leq \alpha ,\beta\leq n} a_{i\,\alpha}^2 b_{\beta\,j}^2=
\left( \dsum_{1\leq i,\alpha \leq n} a_{i\,\alpha}^2\right) \left( \dsum_{1\leq \beta ,j \leq n} b_{\beta\,j}^2\right) \\
&=& \norme{A}_2^2\norme{B}_2^2.
\end{array}
$$
Donc $g(A,B)\leq 1$, ceci prouve que $g$ est bornée et $\sup g\leq 1$. D'autre part, en considérant le même exemple $A=E_{1\,1}$ on trouve
$\boxed{\sup g =1 }$.
Pour la fonction $h$, l'estimation est plus simple.
$$ \norme{AB}_\infty =\max_{1\leq i,j\leq n}\abs{\dsum_{k=1}^na_{i\,k}b_{k\,j}}\leq \max_{1\leq i,j\leq n}\dsum_{k=1}^n\abs{a_{i\,k}}\abs{b_{k\,j}}
\leq \max_{1\leq i,j\leq n}\dsum_{k=1}^n\norme{A}_\infty\norme{B}_\infty =n\norme{A}_\infty\norme{B}_\infty.
$$
Donc $h(A,B)\leq n$, ceci prouve que $h$ est bornée et $\sup g\leq n$.
considérons la matrice $J$ dont tous les coefficients sont égaux à $1$, on a
$$J\neq 0,\, \norme{J}_\infty =1,\,\, J^2=nJ,\quad h(J,J)=\dfrac{\norme{J^2}_\infty}{\norme{J}_\infty^2}=\dfrac{n}{1}=n.
$$
On en déduit alors
$\boxed{\sup h =n }$.
($\star$)
Correction
Soit $(E,\norme{\cdot})$ un EVN. On définit l'application $f$ sur $E$ par
$f(x)=\dfrac{x}{1+\norme{x}^2}$ pour tout $x\in E$.
-
Montrer que $f$ est continue de $(E,\norme{\cdot})$ dans $(E,\norme{\cdot})$.
-
Montrer que $f(E)=\overline{B}(0,\frac{1}{2})$.
Correction
-
$f$ est la somme produit des fonctions continues
-
Pour tout $x\in E$, $\norme{f(x)}=\dfrac{\norme{x}}{1+\norme{x}^2}$. Une étude rapide de la
fonction $t\longmapsto\dfrac{t}{1+t^2}$, montre que,
$$\forall t\in \R,\,\abs{\dfrac{t}{1+t^2}}\leq \dfrac{1}{2} \Longrightarrow \forall x\in
E,\,f(x)\in \overline{B}(0,\frac{1}{2})$$
ceci montre que $f(E)\subset \overline{B}(0,\frac{1}{2})$.
Inversement, soit $y\in \overline{B}(0,\frac{1}{2})$ non nul. On pose,
$x=\dfrac{1+\sqrt{1-4\norme{y}^2}}{2\norme{y}^2}y$, alors
$$f(x)=\dfrac{\dfrac{1+\sqrt{1-4\norme{y}^2}}{2\norme{y}^2}y
}{1+\norme{\dfrac{1+\sqrt{1-4\norme{y}^2}}{2\norme{y}^2}y}^2}=\dfrac{2(1+\sqrt{1-4\norme{y}^2})}{4\norme{y}^2+(1+\sqrt{1-4\norme{y}^2})^2}y=\dfrac{2(1+\sqrt{1-4\norme{y}^2})}{2+2\sqrt{1-4\norme{y}^2}}y=y$$
ceci prouve que $y\in f(E)$, donc $\overline{B}(0,\frac{1}{2})\subset f(E)$ d'où
l'égalité.
Remarque.
Pour trouver un antécédent de $y$ par $f$, on résout l'équation
$$\norme{f(x)}=\norme{y}\Longrightarrow \norme{x}=\norme{y}(1+\norme{x}^2) \Longrightarrow
\norme{y}\norme{x}^2-\norme{x}+\norme{y}=0.$$
($\star$)
Correction
Soient $(E,\norme{\cdot})$ un EVN et $a\in E$ non nul, on considère l'application $f$ définie par:
$$\forall x\in E,\quad f(x)=\norme{x-a} \text{ si }\norme{x}\leq \norme{a}, \text{ et } f(x)=0
\text{ sinon }.$$
-
Montrer que $f$ est continue en $a$.
-
Montrer que $f$ n'est pas continue en $-a$.
Correction
-
Il est clair que $f(a)=0$.
Soit $(x_n)$ une suite d'éléments de $E$ qui converge vers $a$, donc
$$\forall \varepsilon>0,\,\exists n_0,\,\forall n\geq n_0,\,\norme{x_n-a}\leq \varepsilon.$$
Pour $n\geq n_0$, si $\norme{x_n}>\norme{a}$ alors $f(x_n)=0$, sinon
$f(x_n)=\norme{x_n-a}\leq \varepsilon$.
Dans les deux cas, pour tout $n\geq n_0$, on a $\abs{f(x_n)}\leq \varepsilon$, ce qui prouve
que
$f(x_n)\tendversN 0=f(a)$.
D'après la caractérisation séquentielle de la continuité, $f$ est continue en $a$.
-
Pour $n\geq 1$, on définit les deux suites : $ u_n=(-1-\frac{1}{n})a,\,
v_n=(-1+\frac{1}{n})a$, il est clair que $u_n\tendversN\,-a$ et $v_n\tendversN\,-a$. D'autre
part, on a
$$\forall n\in \N,\,\norme{u_n}=(1+\frac{1}{n})\norme{a}> \norme{a}\Longrightarrow
f(u_n)=0\tendversN\,0,$$
et
$$\forall n\in \N,\,\norme{v_n}=(1-\frac{1}{n})\norme{a}\leq \norme{a}\Longrightarrow
f(v_n)=\norme{v_n-a}=(2-\frac{1}{n})\norme{a}\tendversN\, 2\norme{a}$$
les deux limites étant différentes, ceci prouve que $f$ n'est pas continue en $-a$.
($\star$)
Correction
Soient $A,\,B$ deux parties d'un EVN de dimension finie, une application $f$ de $A$ dans $B$ est
appelée homéomorphisme de $A$ dans $B$ si elle est bijective, continue ainsi que sa réciproque.
-
Montrer que $f:x\longmapsto \dfrac{x}{1+\abs{x}}$ est un homéomorphisme de $\R$ dans
$]-1,1[$.
-
Montrer que tout EVN de dimension finie est homéomorphe à chacune de ses boules ouvertes.
Correction
-
il est facile de vérifie que $f$ est continue strictement croissante de $\R$ dans
$f(\R)=]-1,1[$. L'application réciproque $g(x)=\dfrac{x}{1-\abs{x}}$
-
Soit $a\in E$, $r\in \R_+^*$. On pose, pour $x\in E$, $f(x)=a+r\dfrac{x}{1+\norme{x}}$.
$f$ est continue sur comme la somme et le produit des fonctions continue.
D'autre par, $f(E)=B(a,r)$. En effet,
- Pour tout $x\in E$,
$$\norme{f(x)-a}=\norme{r\dfrac{x}{1+\norme{x}}} < r\Longrightarrow f(x)\in B(a,r).$$
- Inversement, si $z\in B(a,r)$ , on pose, $x=\dfrac{z-a}{r-\norme{z-a}}$ alors
$$f(x)=a + r\dfrac{\dfrac{z-a}{r-\norme{z-a}}}{1+\dfrac{\norme{z-a}}{r-\norme{z-a}}}=a+r
\dfrac{z-a}{(r-\norme{z-a})+\norme{z-a}}=a+z-a=z$$
ce qui prouve que $z\in f(E)$.
La démarche précédente, montre que $f$ est surjective, montrons maintenant que $f$ est
injective.
Soient $x,\,y\in E$ tels que $f(x)=f(y)$, ce qui donne $\norme{f(x)}=\norme{f(y)}$ donc
$\dfrac{\norme{x}}{1+\norme{x}}=\dfrac{\norme{y}}{1+\norme{y}}$. En utilisant la première
question de l'exercice, on trouve que $\norme{x}=\norme{y}$, on remplace dans la relation,
$$f(x)=f(y)\Longrightarrow \dfrac{x}{1+\norme{x}}
=\dfrac{y}{1+\norme{y}}=\dfrac{y}{1+\norme{x}} \Longrightarrow x=y$$
Ainsi $f$ est injective, donc bijective.
Le calcul de $f^{-1}$ (déjà fait), donne
$\fonct{f^{-1}}{B(a,r)}{E}{x}{\dfrac{x-a}{r-\norme{x-a}}}$, qui est une fonction continue (somme
et produit des fonctions continues).
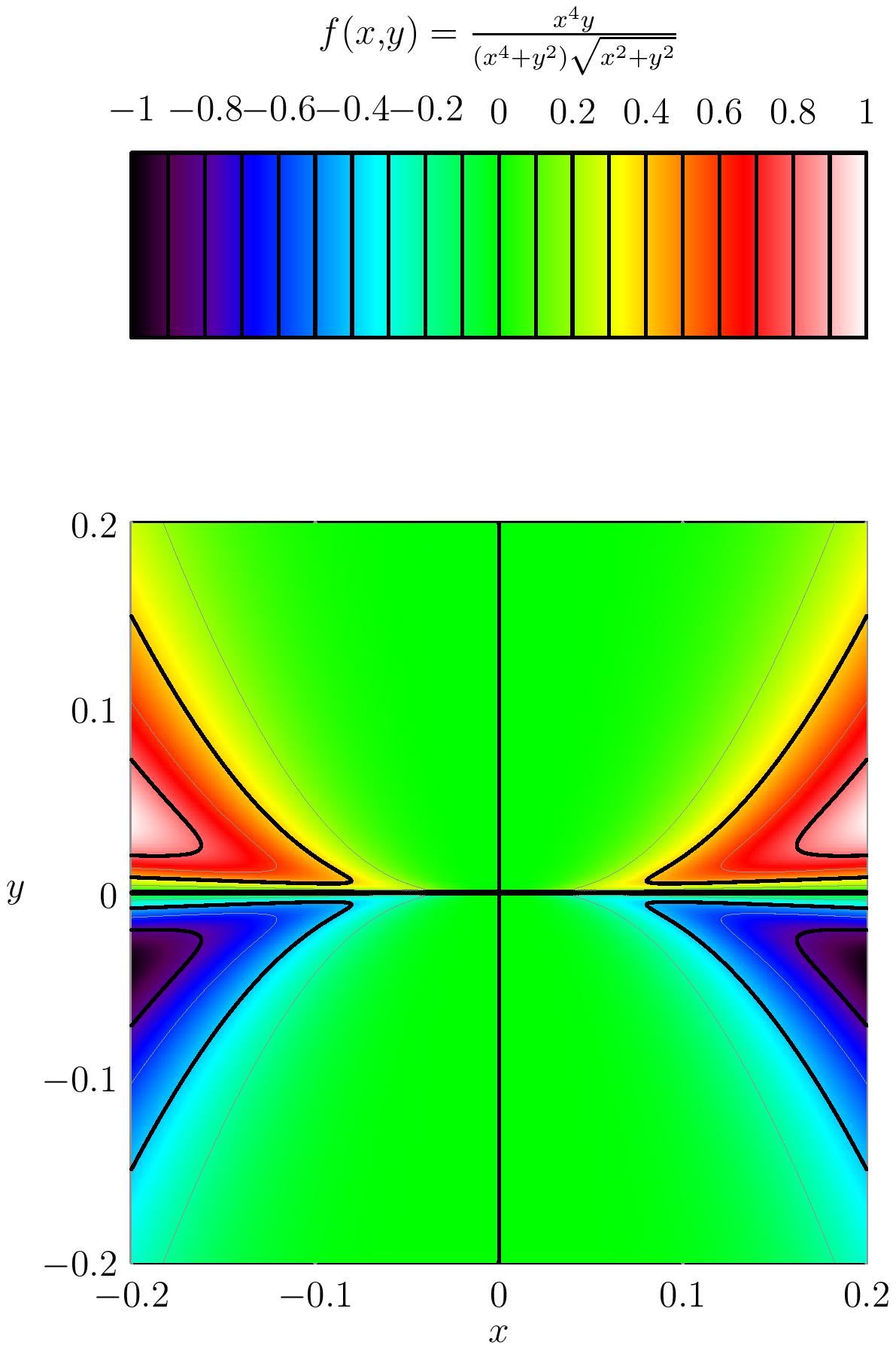
(Mines-Ponts PSI 2017)
Correction
$H$, définie par $H(0,0)=0$ et $H(x,y)=\dfrac{x^4y}{(x^4+y^2)\sqrt{x^2+y^2}}$ pour $(x,y)\neq (0,0)$
est-elle continue en $(0,0)$.
Correction
Soit $(x,y)\in \R^2\setminus \{(0,0)\}$, si $y=0$ alors $H(x,y)=0\tendvers{(x,0)}{(0,0)}0$.
Sinon, on pose $x=r\cos(\theta),\, y=r\sin(\theta)$ avec $r=\sqrt{x^2+y^2}$ et $\theta\in \R$, $\theta\neq 0[\pi]$.
Alors
$$H(x,y)=\dfrac{r^5 \cos(\theta)^4\sin(\theta)}{r^3 (r^2\cos(\theta)^4+\sin(\theta)^2)}=$$
($\star\star$)
Correction
Soit $E$ un $\R$-EVN et $A,\,B$ deux parties non vides de $E$. Soit $f$ une fonction définie sur $A\cup B$ dans
$\R$ telle que $f_{\mid_A}$ et $f_{\mid_B}$ sont continues.
-
On suppose que $A$ et $B$ sont des ouverts de $E$. Montrer que $f$ est
continue.
-
On suppose que $A$ et $B$ sont des fermés de $E$. Montrer que $f$ est continue.
-
Dans le cas générale, peut-on dire que $f$ est continue?
Correction
-
Soit $x\in A\cup B$, soit $x\in A$ ou $x\in B$. Supposons que $x\in A$, comme $A$ est un ouvert de $E$ alors
il existe $r>0$ tel que $B(x,r)\subset A$.
Considérons maintenant une suite $(x_n)$ d'élément de $A\cup B$ telle que $x_n\tendversN\,x$,
d'après la définition de la convergence d'une suite,
$$\exists n_0,\quad \forall n\geq n_0,\quad x_n\in B(x,r).$$
Or $B(x,r)\subset A$ et $f$ est continue sur $A$ donc $f(x_n)\tendversN\,f(x)$ ce qui prouve la continuité de
$f$ en $x$.
-
SSoient $x\in A\cup B$ et $(x_n)_n$ une suite d'éléments de $A\cup B$ telle que $x_n\tendversN\, x$.
On note $I_A=\{n\in \N,\, x_n\in A\}$ et $I_B=\{n\in \N,\, x_n\in B\}\setminus I_A$, de sorte que
$I_A\cap I_B=\emptyset $ et $I_A\cup I_B=\N$.
Si $I_A$ est fini, alors à partir d'un certain rang, tout les termes de la suite $(x_n)$ sont dans $B$, comme $B$ est fermé
alors $\dsp \lim_nx_n =x\in B$, $f$ est continue sur $B$ alors $f(x_n)\tendversN\,f(x)$.
Si $I_B$ est fini, avec le même raisonnement $f(x_n)\tendversN\,f(x)$.
Sinon ($I_A$ et $I_B$ sont infinis) la suite $(x_n)_{n\in I_A}\in A^\N$ converge vers $x$ donc $x\in A$ car $A$ est fermé,
$f$ étant continue sur $A$ alors $(f(x_n))_{n\in I_A}$ converge vers $f(x)$, de même la suite $(f(x_n))_{n\in I_B}$ converge
vers $f(x)$. Comme $I_A\cup I_B=\N$, on en déduit que $f(x_n)\tendversN\,f(x)$.
Conclusion $f(x_n)\tendversN\,f(x)$ ce qui prouve la continuité de $f$.
-
Soit $A=[-1,0]$ et $B=]0,1]$, $f$ définie par $f(x)=0$ si $x\in A$ et $1$ si $x\in B$.
Il est clair que $f_{A}$ est continue, de même pour $f_B$, mais $f$ n'est pas continue sur $A\cup B$.
Fonctions lipschitziennes
($\star\star$)
Correction
Soient $f,\,g$ deux fonctions de $\R$ dans $\R$.
-
On suppose que $f$ est dérivable sur $\R$. Montrer que $f$ est lipschitzienne sur $\R$ ssi
$f'$ est bornée sur $\R$.
-
On suppose que $f,\,g$ sont lipschitziennes et bornées sur $\R$. Montrer que $fg$ est
lipschitzienne sur $\R$. Ce résultats reste-t-il vrai si les fonctions $f,\,g$ ne sont pas
bornées?
-
On suppose que $f$ est lipschitzienne sur $\R$. Montrer qu'ils existe $A,\,B\in \R_+$ tels
que, pour tout $x\in \R$, $\abs{f(x)}\leq A\abs{x}+B$.
-
On suppose que $f$ vérifie la propriété suivante:
$$\exists M>0,\,\forall x,y\in \R,\quad 0\leq x-y\leq 1\Longrightarrow \abs{f(x)-f(y)}\leq
M\abs{x-y}.$$
Montrer que $f$ est lipschitzienne sur $\R$.
Correction
-
Supposons que $f$ lipschitzienne, alors il existe $k>0$ tel que, pour tout $(x,y)\in R^2$, on
a
$\abs{f(x)-f(y)}\leq k\abs{x-y}$.
Soit $x\in \R$, comme $f$ est dérivable en $x$ alors
$\dsp\limiteX{h}{0}\dfrac{f(x+h)-f(x)}{h}=f'(x)$ mais on a
$$\forall h\neq 0,\quad \abs{\dfrac{f(x+h)-f(x)}{h}}\leq k\Longrightarrow
\abs{f'(x)}=\abs{\limiteX{h}{0}\dfrac{f(x+h)-f(x)}{h}}\leq k$$
Ceci prouve que $f'$ est borné sur $\R$ et $\norme{f'}_\infty \leq k$.
-
Soit $x,y\in\R$, on a
$$
\begin{array}{lcl}
\abs{f(x)g(x)-f(y)g(y)}&=&\abs{f(x)g(x)-f(x)g(y)+f(x)g(y)-f(y)g(y)} =\abs{f(x)(g(x)-g(y)) +g(y)(f(x)-f(y))}\\
&&\\
&\leq& \abs{f(x)}\abs{g(x)-g(y)}+\abs{g(y)}\abs{f(x)-f(y)}\leq k_g \abs{f(x)}\abs{x-y}+k_f \abs{g(y)}\abs{x-y}\\
&&\\
&\leq & \left(k_g\norme{f}_\infty +k_f\norme{g}_\infty \right) \abs{x-y}
\end{array}
$$
Ce qui prouve que $fg$ est lipschitzienne.
L'hypothèse $f,\,g$ bornées est indispensable, comme le montre l'exemple $f(x)=g(x)=x$.
-
Supposons que $f$ est lipschitzienne, et soit $x\in \R$, on a
$$\abs{f(x)} =\abs{f(x)-f(0)+f(0)}\leq \abs{f(x)-f(0)}+\abs{f(0)} \leq k \abs{x-0}+\abs{f(0)}$$
ce qui donne le résultat avec $A=k$ et $B=\abs{f(0)}$.
-
Soient $x,y\in \R$, supposons que $x< y$, on note $K_x=\lfloor x \rfloor,\, K_y =\lfloor y \rfloor$. Ensuite, on écrit:
$$f(y)-f(x)=f(y)-f(K_y)+f(K_y)-f(K_x)- (f(x)-f(K_x))=f(y)-f(K_y)+\sum_{j=K_x}^{K_y-1}(f(j+1)-f(j))- (f(x)-f(K_x)).$$
Puis,
$$
\begin{array}{lcl}
\abs{f(y)-f(x)}&=& \abs{f(y)-f(K_y)+\dsum_{j=K_x}^{K_y-1}(f(j+1)-f(j))- (f(x)-f(K_x))}\\
&&\\
&\leq& \abs{f(y)-f(K_y)}+\dsum_{j=K_x}^{K_y-1}\abs{f(j+1)-f(j)}+\abs{f(x)-f(K_x)}\\
&&\\
&\leq & M \abs{y-K_y}+\dsum_{j=K_x}^{K_y-1}M+M\abs{x-K_x}\\
&&\\
&=& M (y-K_y)+M(K_y-K_x)+M(x-K_x)=M (y-x)=M\abs{y-x}
\end{array}
$$
($\star$)
Correction
Soient $E$ un $\K$-evn et $T:E \to E$ définie par $T(u) = \left\{ {
\begin{array}{ll}
u & {{\text{si }}\left\| u \right\| \leqslant 1} \\
{\frac{u}{{\left\| u \right\|}}} & {{\text{sinon}}} \\
\end{array}
} \right.$.
Montrer que $T$ est 2-lipschitzienne.
Correction
Soient $u,v\in E$,
-
Si $\norme{u}\leq 1$ et $\norme{v}\leq 1$, on a immédiatement
$$\norme{T(u)-T(v)}=\norme{u-v}\leq 2\norme{u-v}.$$
-
Si $\norme{u}> 1$ et $\norme{v}> 1$, en utilisant le résultat de l'exercice
\ref{Ex:InegaliteNorme}, on trouve:
$$\norme{T(u)-T(v)}= \norme{\dfrac{u}{\norme{u}}-\dfrac{v}{\norme{v}}}\leq
\max(\norme{u},\norme{v})\norme{\dfrac{u}{\norme{u}}-\dfrac{v}{\norme{v}}}\leq
2\norme{u-v}.$$
-
Si $\norme{u}\leq 1$ et $\norme{v}>1$, on a alors:
$$\begin{array}{lcl}
\norme{T(u)-T(v)}&=& \norme{u-\dfrac{v}{\norme{v}}}=\norme{u-v+v-\dfrac{v}{\norme{v}}}\\
&\leq & \norme{u-v}+\norme{\left(1-\frac{1}{\norme{v}}\right)v}=\norme{u-v}+\norme{v}-1\\
&\leq & \norme{u-v}+\norme{v}-\norme{u}\leq 2\norme{u-v}
\end{array}$$
-
Si $\norme{v}\leq 1$ et $\norme{u}>1$, ce cas est équivalent au cas précédent.
Donc, dans tous les cas, on a: $\norme{T(u)-T(v)}\leq 2\norme{u-v}$ ce qui prouve le résultat.
($\star$)
Correction
Soit $(a,b)\in (\R_+)^2$. On considère l'application $\fonct{F}{\R^2}{\R^2}{(x,y)}{(ay,bx)}$.
Montrer que $f$ est lipschitzienne.
Correction
On munit $\R^2$ de la norme $\norme{(x,y)}=\abs{x}+\abs{y}$. Il est clair que, pour tou $(x,y),\,(u,v)\in \R^2$,
$$\begin{array}{lcl}
\norme{f((x,y))-f((u,v))}&=&\norme{(a(y-v),b(x-u))}
=\abs{a}\abs{y-v}+\abs{b}\abs{x-u}\\
&&\\
&\leq& \max\{\abs{a},\abs{b}\}\norme{(x,y)-(u,v)}.
\end{array}$$
Ce qui prouve que $f$ est lipschitzienne.
Remarque: on aurait pu utiliser la linéarité de $f$, car toute application linéaire continue est
lipschitzienne.
($\star\star$)
Correction
Soit $f$ une fonction définie sur $\R_+$, $k$-lipschitzienne. On définie la fonction $F$ par
$$F(0)=f(0),\quad \text{ et pour } x>0,\, F(x)=\dfrac{1}{x}\int_0^xf(t)\ud t.$$
-
Montrer qu'on peut écrire $F(x)=\dsp\int_0^1f(xt)\ud t$.
-
En déduire que $F$ est $\frac{k}{2}$-lipschitzienne.
Correction
-
Si $x>0$, on définit le changement de variable $u=\dfrac{t}{x}$, ce qui donne $\ud t =x\ud u$
$$F(x)=\dfrac{1}{x}\int_0^xf(t)\ud t=\dfrac{1}{x}\int_0^1f(xu)(x\ud u)=\int_0^1f(xu)\ud u$$
Cette relation reste vrai pour $x=0$, puisque $F(0)=f(0)=\dsp\int_0^1f(0)\ud u$.
-
Soient $x,y\in \R_+$, on a
$$\abs{F(x)-F(y)}\leq \int_0^1\abs{f(xu)-f(yu)}\ud u\leq \int_0^1k\abs{xu-yu}\ud
u=k\abs{x-y}\int_0^1u\ud u =\dfrac{k}{2}\abs{x-y}.$$
Limites
($\star$)
Correction
Pour $a\in \R$, pour tout $x\in \R^*$, on pose $f(x)=\dfrac{a+\sin \left(1/x\right)}{x}$. Étudier,
en fonction de $a$, les limites à droite et à gauche de $f$ en $0$.
Correction
On distingue deux cas:
-
$\abs{a}>1$, dans cas pour tout $x\neq 0$, on a $\sin\left(\frac{1}{x}\right)+a$ de même
signe que $a$ car $\abs{\sin\left(\frac{1}{x}\right)}\leq 1$, on en déduit alors
$$\dfrac{a+\sin \left(1/x\right)}{x}\tendvers{x}{0^+}\,\varepsilon\,\infty,\quad
\dfrac{a+\sin \left(1/x\right)}{x}\tendvers{x}{0^-}\,-\varepsilon\,\infty,\quad\text{avec
}\varepsilon=\dfrac{a}{\abs{a}}.$$
-
$\abs{a}\leq 1$, dans ce cas on n'a pas de limite en $0$. En effet, considérons les deux
suites,
$$\forall n\geq 1,\quad u_n=\dfrac{1}{-\Arcsin(a)+2\pi n},\,\quad
u_n=\dfrac{1}{\Arcsin(a)+2\pi n}. \quad u_n\tendversN\,0,\,
v_n\tendversN 0.$$
et on a $f(u_n)=0\tendversN\,0$ et $f(v_n)=(2a)(\Arcsin(a)+2\pi n)\tendversN
\,\frac{a}{\abs{a}}\infty$. Donc les deux limites sont différentes. (si $a=0$, on peut
prendre $v_n=\dfrac{2}{\pi+4n\pi}$).
($\star$)
Correction
Soient $a,\,b\in \R_+^*$. Calculer les limites suivantes:
$$\limiteX{x}{0^+}\dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right),\quad
\limiteX{x}{0^+}\dfrac{b}{x}\mathrm{E}\left(\frac{x}{a}\right),\quad
\limiteX{x}{0^-}\dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right),\quad
\limiteX{x}{0^-}\dfrac{b}{x}\mathrm{E}\left(\frac{x}{a}\right).$$
Correction
Pour tout $x\in \R^*$, on a:
$$\frac{b}{x}\leq \mathrm{E}\left(\frac{b}{x}\right)< \frac{b}{x}+1\Longrightarrow
\left\{\begin{array}{lc}
\forall x>0,&\frac{b}{a}\leq \dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right) <
\frac{b}{a}+\dfrac{x}{a}\\
&\\
\forall x< 0,&\frac{b}{a}+\dfrac{x}{a}< \dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right)\leq
\frac{b}{a}
\end{array}
\right.\Longrightarrow
\limiteX{x}{0^+}\dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right)=\limiteX{x}{0^-}\dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right)=\dfrac{b}{a}.
$$
D'autre part pour $x$ assez proche de $0^+$ on va avoir $x< a$ donc
$\mathrm{E}\left(\frac{x}{a}\right)=0$ d'où
$\dsp\limiteX{x}{0^+}\dfrac{b}{x}\mathrm{E}\left(\frac{x}{a}\right)=0$.
En revanche, pour $x$ proche de $0^-$, on a $\mathrm{E}\left(\frac{x}{a}\right)=-1$ d'où
$\dsp\limiteX{x}{0^-}\dfrac{b}{x}\mathrm{E}\left(\frac{x}{a}\right)=\infty$.
($\star$)
Correction
-
Soit $f:\R \to \R$ une fonction périodique. Montrer que si $f$ admet une limite finie en
$+\infty$, alors $f$ est constante.
-
Montrer que la fonction $\sin$ n'a pas de limite en $+\infty$.
-
Montrer que l'application $\fonct{f}{\R^*}{\R}{x}{\sin\left(\dfrac{1}{x}\right)}$ n'a pas de
limite en $0^+$.
Correction
-
Supposons que $f$ est $T$-périodique avec $T>0$ et $f$ admet une limite $\ell$ en $\infty$.
Montrons que $f$ est constante.
D'après la caractérisation séquentielle de la limite, pour tout suite $(x_n)$ tel que
$x_n\tendversN\,\infty$, on a $f(x_n)\tendversN\,\ell$. Soit maintenant $x\in \R$, on définit
la suite $(x_n)$ par $x_n=x+n\times T$, alors $x_n\tendversN\infty$ donc
$f(x_n)\tendversN\ell$, or comme $f$ est $T$-périodique on a $f(x_n)=f(x)$, on en déduit que
$f(x)=\ell$ ce qui prouve que $f$ est constante.
-
Si la fonction $\sin$ admettait une limite en $\infty$ elle serait constante d'après la
question précédente (puisque $\sin$ est une fonction périodique). Or la fonction $\sin$ n'est
pas constate ( par exemple $\sin(0)=\cdots \neq \cdots =\sin(\pi/2)$.
On en déduit alors que limite $\sin$ en $\infty$ n'existe pas.
-
Si $x\mapsto \sin(1/x)$ admet une limite en $0^+$ alors en utilisant le résultat sur la
composition des limites on aurait $y\mapsto \sin(y)$ admet une limite en $+\infty$. Ce qui
n'est pas le cas!
($\star$)
Correction
Soient $E$ un $\K$-evn et $A\subset E$ non vide et $a\in E$. Soit $f:A\longmapsto \K$, on suppose
que $f$ admet une limite $\beta \neq 0$ en $a$.
-
Montrer qu'il existe $r>0$ tel que, pour tout $x\in B=B_f(a,r)\cap A$, on a $f(x)\neq 0$.
-
Montrer que $\dfrac{1}{f}$ est bien définie sur $B$ et que $\dfrac{1}{f}$ admet
$\dfrac{1}{\beta}$ au point $a$.
Correction
-
On applique la définition de la limite, avec $\varepsilon =\frac{\abs{\beta}}{2}$, ce qui
donne:
$$\exists r>0,\quad \forall x\in B_f(a,r)\cap A,\, \abs{f(x)-\beta}\leq
\dfrac{\abs{\beta}}{2},$$
or $\abs{\abs{f(x)}-\abs{\beta}}\leq \abs{f(x)-\beta}$, ce qui donne
$$\forall x\in B_f(a,r)\cap A,\, \abs{\abs{f(x)}-\abs{\beta}}\leq\abs{f(x)-\beta}\leq
\dfrac{\abs{\beta}}{2}\Longrightarrow \forall x\in B_f(a,r)\cap A,\,
\dfrac{\abs{\beta}}{2}\leq\abs{f(x)}\leq \dfrac{3\abs{\beta}}{2}.$$
Autrement dit, $\forall x\in B_f(a,r)\cap A,\quad f(x)\neq 0$.
-
Puisque $f$ ne s'annule pas sur $B=B_f(a,r)\cap A$, alors la fonction
$\fonct{g}{B}{\K}{x}{\frac{1}{f(x)}}$
est bien définie.
D'autre part, en utilisant l'hypothèse sur $f$, on a:
$$\forall \varepsilon>0, \exists \eta>0,\quad \forall x\in B_f(a,\eta)\cap A,\,
\abs{f(x)-\beta}\leq \dfrac{\abs{\beta}^2\varepsilon}{2}.$$
Posons $\alpha=\min (\eta,r)$, on a alors,
$$\forall x\in \left(B_f(a,\alpha)\cap A\right)\subset
B,\,\abs{g(x)-\dfrac{1}{\beta}}=\abs{\dfrac{\beta
-f(x)}{f(x)\beta}}=\dfrac{\abs{f(x)-\beta}}{\abs{\beta}\abs{f(x)}}\leq
\dfrac{2\abs{f(x)-\beta}}{\abs{\beta}^2}\leq \varepsilon.$$
Ce qui prouve que $g$ admet une limite en $a$ selon $B$.
($\star$)
Correction
Étudier la limite éventuelle en $(0,0)$ de :
a) $f(x,y)=\dfrac{x^3+xy^2-2xy}{x^2+y^2}\quad\quad$
b) $g(x,y)=\dfrac{x^4+y^4+2x^2y}{\sqrt{x^2+y^2}}\quad\quad$
c) $h(x,y)=\dfrac{x^3-y^3}{ (x^2+y^2)^{3/2}}$
Correction
-
Pour $x\in \R^*$, on a
$$f(x,x)=\dfrac{2x^3-2x^2}{2x^2}=x-\dfrac{1}{2}\tendvers{x}{0}\dfrac{-1}{2},\quad
f(x,0)=\dfrac{x^3}{x^2}=x\tendvers{x}{0}\,0.$$
Les deux limites étant différentes, on en déduit que $f$ n'admet pas de limite en $(0,0)$.
-
Pour tout $(x,y)\in \R^2\setminus\{(0,0)\}$, on a:
$$\abs{g(x,y)}\leq \dfrac{2\norme{(x,y)}_2^4+2\norme{(x,y)}_2^3}{\norme{(x,y)}_2}\leq
2\norme{(x,y)}_2^3+2\norme{(x,y)}_2^2\tendvers{(x,y)}{(0,0)}\,0.$$
Donc $g$ admet $0$ comme limite en $(0,0)$.
-
Pour $x\in \R^*$, on a
$$h(x,0)=\dfrac{x^3}{\sqrt{x^2}^3}=\dfrac{x^3}{\abs{x}^3}\Longrightarrow
h(x,0)\tendvers{x}{0^+}\,1 \text{ et }h(x,0)\tendvers{x}{0^-}\,-1,$$
donc $h$ n'admet pas de limite en $(0,0)$.
($\star$)
Correction
L'application $\fonct{f}{\R^3\setminus
\{0\}}{\R^3}{(x,y,z)}{\dfrac{(x,y,z)}{\sqrt{x^2+y^2+z^2}}-(x,y,z)}$ admet-t-elle une limite en $0$?
Correction
Rappelons que $\sqrt{x^2}=\abs{x}$...
-
[$\triangleright$] Soit $x\in \R_+^*$, on a:
$$f(x,x,x)=\dfrac{(x,x,x)}{\sqrt{x^2+x^2+x^2}}-x(1,1,1)=(\dfrac{1}{\sqrt{3}}-x)(1,1,1)\tendvers{x}{0^+}\dfrac{1}{\sqrt{3}}(1,1,1).$$
-
[$\triangleright$] Soit $x\in \R_-^*$, on a:
$$f(x,x,x)=\dfrac{(x,x,x)}{\sqrt{x^2+x^2+x^2}}-x(1,1,1)=(\dfrac{-1}{\sqrt{3}}-x)(1,1,1)\tendvers{x}{0^-}\dfrac{-1}{\sqrt{3}}(1,1,1).$$
On en déduit que $\dsp\lim_{(x,y,z)\to(0,0,0)} f(x,y,z)$ n'existe pas.
($\star$)
Correction
Soit $f \colon \R^2 \setminus \{(0,0)\} \to \R\,$ la fonction définie par: $\dsp f(x,y) =
\frac{x^2y^2}{x^2y^2 + (x-y)^2}$. Montrer que $\dsp \lim_{x\to 0}\lim_{y\to 0}f(x,y) = \lim_{y\to
0}\lim_{x\to 0}f(x,y) = 0$, et que $\dsp \lim_{(x,y)\to (0,0)} f(x,y)$ n'existe pas.
Correction
On a, pour $x\neq 0$,
\[
\lim_{y\to 0}f(x,y) = \lim_{y\to 0}\frac{y^2}{y^2 + (1-y/x)^2}
=\dsp\frac{\dsp\lim_{y\to 0} y^2}{\dsp\lim_{y\to 0} y^2 + (1-y/x)^2}
=\frac{0}{1} =0,
\]
donc $\dsp \lim_{x\to 0}\lim_{y\to 0}f(x,y)=0$.
De même $\lim_{y\to 0}\lim_{x\to 0}f(x,y) = 0$ puisque $f(x,y)=f(y,x)$ d'où le résultat.
D'autre part, pour $x\neq 0$, $f(x,x) = \dfrac{x^4}{x^4} =1$ d'où
$\dsp\lim_{x\to 0}f(x,x) = 1$ et $f(x,2x)=\dfrac{x^4}{5x^4} =4/5$. Donc
$\dsp\lim_{(x,y)\to (0,0)} f(x,y)$ ne peut pas exister.
(www)
Correction
Soit $f : \R^2 \to \R$, définie par $ f(x,y) = \left\{\begin{array}{cc}
(x+y)\sin \frac{1}{x} \sin \frac{1}{y} & \text{ si }xy \neq 0 \\
0 & \text{ si } xy = 0
\end{array}\right .$.
Démontrer que les deux limites itérées $\dsp\lim_{x\to 0}\lim_{y\to 0}f(x,y)$ et $\dsp \lim_{y\to
0}\lim_{x\to 0}f(x,y)$ n'existent pas, et que $\dsp \lim_{(x,y)\to (0,0)}f(x,y)$ existe et est
égale à $0$.
Correction
Soient $x,y\in \R$ tels que $xy\neq 0$, on a
$$f(x,y)= x\left(\sin \frac{1}{x} \sin \frac{1}{y}\right) +y\left(\sin \frac{1}{x} \sin
\frac{1}{y}\right) =xb(x,y)+yb(x,y),\,\text{ avec } b(x,y)=\sin \frac{1}{x} \sin \frac{1}{y}.$$
La fonction $b$ est bornée mais elle n'admet pas de limite lorsque $y$ tend vers $0$ (c.f.
cours). On en déduit que $\dsp\lim_{y\to 0} xb(x,y)$ n'existe pas donc $\dsp\lim_{y\to 0} f(x,y)$
n'existe pas (
bien que $\dsp\lim_{y\to 0} yb(x,y)$ existe!).
Donc $\dsp\lim_{x\to 0}\lim_{y\to 0}f(x,y)$ n'existe pas ! De même pour $\dsp \lim_{y\to
0}\lim_{x\to 0}f(x,y)$ puisque $f(x,y)=f(y,x)$.
En revanche, on a pour tout $(x,y)\in \R^2$, avec $xy\neq 0$,
$$\abs{f(x,y)}\leq \abs{b(x,y)}(\abs{x}+\abs{y})\leq
2\norme{(x,y)}_\infty\tendvers{(x,y)}{(0,0)}\,0 $$
Pour $(x,y)\in \R^2$ tels que $xy=0$, on a $f(x,y)=0$. On en déduit alors $\dsp \lim_{(x,y)\to
(0,0)}f(x,y)=0$
Soient $E$ et $F$ deux espace vectoriels normés. On suppose qu'une suite $(f_n )$ d'éléments de $\LL_\mathcal{C}(E,F)$ converge vers $f \in \LL_\mathcal{C}(E,F)$ (au sens de la norme subordonnée) et qu'une suite $(x_n )$ d'éléments de $E$ converge vers $x \in E$. Établir que $f_n (x_n ) \tendversN f(x)$.
Notons $N$ la norme sur $\LL_\mathcal{C}(E,F)$, alors (rappelle de cours!) $$\forall f\in \LL_\mathcal{C}(E,F),\,\,\forall x\in E,\quad \norme{f(x)}_F\leq N(f)\norme{x}_E.$$ Soit $(f_n)$ une suite d'éléments de $\LL_\mathcal{C}(E,F)$ qui converge vers $f\in \LL_\mathcal{C}(E,F)$ et $(x_n)$ une suite d'éléments de $E$ qui converge vers $x$. Alors pour tout $x\in E$, on a $$\begin{array}{lcl} \norme{f(x)-f_n(x_n)}&=& \norme{f(x)-f(x_n)+f(x_n)-f_n(x_n)}\\ &&\\ &\leq &\norme{f(x)-f(x_n)}+\norme{f(x_n)-f_n(x_n)}=\norme{f(x-x_n)}+\norme{(f-f_n)(x_n)}\\ &&\\ &\leq& N(f)\norme{x-x_n}_E+N(f-f_n)\norme{x_n}\tendversN\,0 \end{array}$$ La suite $(x_n)$ étant convergent donc bornée, donc $N(f-f_n)\norme{x_n}\tendversN\,0$, de même $N(f)\norme{x-x_n}_E\tendversN\,0$. On en déduit finalement que $f_n(x_n)\tendversN\,f(x)$.
Soient $E$ et $F$ deux espaces vectoriels normés et $f \in \LL(E,F)$. On suppose que, pour toute suite $(u_n )$ tendant vers $0$, $f(u_n )$ est bornée. Montrer que $f$ est continue.
Supposons que $f$ n'est pas continue, alors $$\forall n\in \N^*,\, \exists x_n \in E\setminus\{0\},\,\, \norme{f(x_n)}_F\geq n\norme{x_n}_E.$$ On pose alors $z_n=\dfrac{x_n}{\sqrt{n}\norme{x_n}_E}$, on a $\norme{z_n}=\dfrac{1}{\sqrt{n}}$ donc $z_n\tendversN\,0$. D'autre part, on a $$\norme{f(z_n)}_F= \norme{f\left(\dfrac{x_n}{\sqrt{n}\norme{x_n}_E}\right)}_F=\dfrac{1}{\sqrt{n}\norme{x_n}_E}\norme{f(x_n)}_F\geq \dfrac{n\norme{x_n}_E}{\sqrt{n}\norme{x_n}_E}=\sqrt{n}\tendversN\,\infty$$ ce qui contredit l'hypothèse. Donc $f$ est continue.
Soient $E$ un espace vectoriel normé non réduit à $\left\{ 0 \right\}$ et $u,v \in \LL(E)$ continus tels que $$u \circ v - v \circ u = \alpha \mathrm{Id}e $$ pour un certain $\alpha \in \mathbb{R}$.
- Établir que pour tout $n \in \N$, $u \circ v^{n + 1} - v^{n + 1} \circ u = (n + 1)\alpha v^n$.
- En déduire que $\alpha = 0$.
- Par récurrence sur $n\in \N$, la relation est vraie pour $n=0$. Soit $n\geq 0$ et supposons que la relation est vraie au rang $n$ i.e. $u \circ v^{n +1} - v^{n +1} \circ u = (n+1) \alpha v^{n}$. $$\begin{array}{lcl} u \circ v^{n + 2} - v^{n + 2} \circ u& =&(u \circ v^{n+1})\circ v - v^{n+1} \circ (v \circ u)\\ &=& ((n+1)\alpha v^{n} +v^{n+1}\circ u)\circ v- v^{n+1}(u\circ v-\alpha\mathrm{Id}e)\\ &=&(n+1)\alpha v^{n+1}+v^n\circ u\circ v-v^{n+1}\circ u\circ v+\alpha v^{n+1}=(n+2)v^{n+1} \end{array}$$ Ceci montre que la relation est vraie au rang $n+1$.
- Notons $\Norme{\phantom{f}}$ la norme subordonné sur $\LL_\mathcal{C}(E,F)$, (rappel.. $$\forall f\in \LL_\mathcal{C}(E,F),\quad \forall x\in E,\quad\norme{f(x)}_F\leq \Norme{f}\,\norme{x}_E.$$ La relation précédente, implique que, pour tout $n\in \N$, $$ \abs{\alpha}(n+1)\Norme{v^{n}}=\Norme{u \circ v^{n + 1} - v^{n + 1} \circ u }\leq \Norme{u\circ v\circ v^n}+\Norme{v^n\circ v\circ u}\leq \left(\Norme{u\circ v}+\Norme{v\circ u}\right) \Norme{v^{n}}$$ Ceci implique que $\abs{\alpha}\Norme{v^{n}}=0$ (il suffit de prendre $n\geq \left(\Norme{u\circ v}+\Norme{v\circ u}\right)$ dans la dernière relation), donc soit $\alpha=0$ ou $v^n=0$. Si on suppose que $v^n=0$, alors en utilisant la relation de récurrence (au rang $n-1$) on trouve que $v^{n-1}=0$ en répétant la même démarche, on trouve que $v=0$, ce qui donne $\alpha\mathrm{Id}e =0$ donc $\alpha=0$. Dans les deux cas, on trouve $\alpha=0$ CQFD.
On munit $\R[X]$ de la norme $\norme{\cdot}_{\infty}$. Étudier la continuité des applications linéaires : $$f_0:P \mapsto P(x_0) \ (x_0\in \R),\quad \qquad f_1:P \mapsto P',\quad \qquad f_2:P \mapsto (X-1)P.$$ Lorsqu'elles sont continues, calculer leur norme. Rappel: Si $P=\dsum_{k=0}^na_kX^k$, alors $\norme{P}=\dsp\max_{k\in \inter{0,n}}(|a_k|)$.
-
$f(P)=P(x_0)$.
Soit $P=\dsum_{k=0}^n a_kX^k\in \R[X]$ avec $n=\deg (P)$, alors
$$\abs{f(P)}=\abs{P(x_0)}=\abs{\dsum_{k=0}^n a_kx_0^k}\leq
\dsum_{k=0}^n\abs{a_k}\abs{x_0}^k\leq \norme{P}_\infty
\dsum_{k=0}^n\abs{x_0}^k=\norme{P}_\infty \dfrac{1-\abs{x_0}^{n+1}}{1-\abs{x_0}}.$$
Alors, on distingue deux cas,
- Si $x_0\in ]-1,1[$ alors $f$ est continue, et $\Norme{f}\leq \dfrac{1}{1-\abs{x_0}}$, d'autre part, en posant pour $n\in \N$, $P=\dsum_{k=0}^n X^k $ (si $x_0\in [0,1[$) ou $P=\dsum_{k=0}^n(-1)^kX^k$ si $x\in ]-1,0[$, on trouve $$f(P)=\dsum_{k=0}^n\abs{x_0}^k=\dfrac{1-\abs{x_0}^{n+1}}{1-\abs{x_0}}\leq \Norme{f}\norme{P}=\Norme{f} \Longrightarrow \Norme{f}\geq \dfrac{1-\abs{x_0}^{n+1}}{1-\abs{x_0}}.$$ On en déduit alors que $\Norme{f}=\dfrac{1}{1-\abs{x_0}}$.
- Si $\abs{x_0}\geq 1$ alors $f$ n'est pas continue.
- $f(P)=P'$. On pose, pour $n\in \N^*$, $P_n=X^n$, alors $\norme{P_n}=1$ et $\norme{f(P_n)}=\norme{nX^{n-1}}=n$, comme $\dfrac{\norme{f(P_n)}}{\norme{P}}\tendversN\,\infty$, alors $f$ n'est pas continue.
- $f(P)=(X-1)P$. Soit $P=\dsum_{k=0}^na_kX^k$, alors $$f(P)=\dsum_{k=0}^na_kX^{k+1}-\dsum_{k=0}^n a_kX^k=-a_0+\dsum_{k=1}^n(a_{k-1}-a_k)X^k+a_nX^{n+1}\Longrightarrow \norme{f(P)}\leq 2\norme{P}$$ on en déduit que $f$ est continue et $\Norme{f}\leq 2$. D'autre part, $f(1-X)=(X-1)(1-X)=-1+2X-X^2$, donc $\norme{f(1-X)}=2=2\norme{1-X}$ ce qui implique que $\Norme{f}=2$.
Soit $E$ un $\R$ e.v.n, et $\varphi$ une forme linéaire non nulle sur $E$. Soit $H=\Ker (\varphi)$.
- Montrer que $\varphi$ est continue si et seulement si $H$ est fermé dans $E$.
- On suppose $H$ fermé. Montrer que, pour tout $a \notin H \ , \ \|\varphi\|= \dsp \frac{|\varphi(a)|} {\ud (a,H)}$.
- Puisque $\Ker (\varphi)=\varphi^{-1}(\{0\})$, donc si $\varphi$ est continue alors $\Ker (\varphi)$ est un fermé de $E$ (image réciproque d'un fermé par une application continue). Inversement, supposons que $H$ est un fermé de $E$, et montrons que $\varphi$ est continue. Supposons que $\varphi$ n'est pas continue, ce qui implique que $\varphi$ n'est pas bornée sur la boule unité, donc il existe une suite $(x_n)$ d'éléments de $B(0,1)$ tel que $\abs{\varphi(x_n)}$ tend vers $\infty$ lorsque $n$ tend vers $\infty$. En particulier, $$\exists N\geq 0,\, \forall n\geq N,\, \abs{\varphi(x_n)}>1\Longrightarrow\forall n\geq N,\, x_n\not\in H.$$ On définit alors la suite $z_n=\dfrac{\varphi(x_N)}{\varphi(x_n)}x_n-x_N$ (pour $n\geq N$), on vérifie facilement que $z_n\in H$, de plus $z_n\tendversN -x_N$, comme $H$ est fermé alors $x_N\in H$ ce qui est absurde! On en déduit alors que $\varphi$ est continue.
- Soit $a\not\in H$, alors $$\forall y\in H,\quad f(a)=f(a-y)\Longrightarrow \forall y\in H,\,\abs{f(a)}=\abs{f(a-y)}\leq \norme{f}\norme{a-y}\Longrightarrow \abs{f(a)}\leq \norme{f}\ud(a,H).$$ Ce qui donne $\dfrac{\abs{\varphi(a)}}{\ud (a,H)}\leq \norme{f}$. D'autre part, pour tout $y\in E\setminus H$, on a $$f\left(a-\frac{f(a)}{f(y)}y\right)=0\Longrightarrow a-\frac{f(a)}{f(y)}y\in H.$$ On obtient alors, $$\norme{\frac{f(a)}{f(y)}y}=\norme{a-(a-\frac{f(a)}{f(y)}y)}\geq \ud (a,H)$$ ce qui donne, $\abs{f(y)}\leq \dfrac{\abs{f(a)}}{\ud (a,H)}\norme{y}$, cette dernière relation reste vraie si $y\in H$, ainsi on a montré $$\forall y\in E, \abs{f(y)}\leq \dfrac{\abs{f(a)}}{\ud (a,H)}\norme{y}\Longrightarrow \norme{f}\leq \dfrac{\abs{f(a)}}{\ud (a,H)}$$
Soit $E = \CC(\left[ {0,1} \right],\mathbb{R})$ muni de $\left\| {\,.\,} \right\|_\infty $.
- Montrer que pour toute fonction $f \in E$, il existe une unique primitive $F$ de $f$ vérifiant $\dsp\int_0^1 {F(t)\,{\mathrm{d}}t} = 0$.
- Établir que l'application $u:f \mapsto F$ est un endomorphisme continu.
- Justifier $\dsp F(x) = \int_0^1 {\left( {\int_t^x {f(u)\,{\mathrm{d}}u} } \right)\,{\mathrm{d}}t} $.
- Calculer $\left\| u \right\|$.
- Pour l'unicité: Si $F_1,\,F_2$ sont deux primitives de $f$ alors il existe $\alpha\in \R$ tel que $F_1=F_2+\alpha$, donc $0=\dsp\int_0^1F_1=\dsp\int_0^1(F_2+\alpha)=\alpha$ ce qui donne $F_1=F_2$. Pour l'existence: On pose $F(x)=\dsp\int_0^xf(t)\ud t -\int_0^1\left(\int_0^xf(u)\ud u\right)\ud x$. Alors $F'=f$ et $\dsp\int_0^1F=0$ donc $F$ est une fonction qui convient.
- Il est clair que $u\in \mathscr{L}(E)$, pour montrer que $u$ est continue il suffit de montrer que $$\exists k>0,\,\forall f\in E,\quad \norme{u(f)}_\infty\leq \norme{f}_\infty,\quad \text{i.e. }, \forall x\in [0,1],\quad \abs{F(x)}\leq k\abs{f(x)}.$$ Soit $f\in E$, on a, $$\begin{array}{lcl} \forall x\in [0,1],\quad \abs{u(f)(x)}&=&\dsp \abs{\int_0^xf(u)\ud u - \int_0^1\left(\int_0^uf(t)\ud t\right)\ud u}\\ &\leq &\dsp \norme{f}_\infty x+\int_0^1\norme{f}_\infty u\ud u \leq \dfrac{3}{2}\norme{f}_\infty\\ &&\Longrightarrow\norme{u(f)}_\infty\leq \dfrac{3}{2}\norme{f}_\infty. \end{array}$$ Ceci prouve la continuité de $u$.
- Soient $f\in E,\,\,t,x\in [0,1]$, on a $\dsp\int_t^xf(u)\ud u=F(x)-F(t)$, donc $$ \int_0^1\left( \int_t^x f(u)\,\ud u \right)\,\ud t=\int_0^1(F(x)-F(t))\ud t=F(x)\int_0^1\ud t -\int_0^1F(t)\ud t=F(x).$$
- Soit $f\in E$, en utilisant la relation précédente, on a pour tout $x\in [0,1]$ $$\begin{array}{lcl} \abs{u(f)(x)}&=&\dsp \abs{\int_0^1\left( \int_t^x f(u)\,\ud u \right)\,\ud t}\\ &&\\ &\leq &\dsp \int_0^1\abs{\int_t^xf(u)\ud u}\ud t\leq \int_0^1\norme{f}_\infty\abs{x-t}\ud t\\ &&\\ &=&\dsp \norme{f}_\infty\left(\int_0^x(x-t)\ud t+\int_x^1(t-x)\ud t\right)\\ &&\\ &=&\dsp \norme{f}_\infty\left(\frac{x^2}{2}+\frac{(1-x)^2}{2}\right)\leq \frac{\norme{f}_\infty}{2}\Longrightarrow \norme{u(f)}_\infty\leq \dfrac{1}{2}\norme{f}_\infty. \end{array}$$ On en déduit que $\norme{u}\leq \frac{1}{2}$. D'autre part, en prenant $f=1$ on trouve que $u(f)(x)=x-\frac{1}{2}$ ce qui donne $\norme{u(f)}_\infty=\frac{1}{2}\norme{f}_\infty$ donc $\norme{u}\geq \frac{1}{2}$. Conclusion, $\norme{u}=\dfrac{1}{2}$.
Soit $E$ un $\K$-espace vectoriel de dimension finie. Montrer que toutes les normes sur $E$ sont équivalents.
Soient $N_1,\,N_2$ deux normes définies sur $E$. Puisque $E$ est de dimension finie, alors $\mathrm{Id}e$ est continue de $(E,N_1)$ dans $(E,N_2)$, donc, \begin{equation} %\label{Eq22-1} \exists K_1>0,\quad \forall x\in E,\, N_1(\mathrm{Id}e (x))=N_1(x)\leq K_1 N_2(x).\quad\quad (Eq-1) \end{equation} De même $\mathrm{Id}e$ est continue de $(E,N_2)$ dans $(E,N_1)$, donc, \begin{equation} % \label{Eq22-2} \exists K_2>0,\quad \forall x\in E,\, N_2(\mathrm{Id}e (x))=N_2(x)\leq K_2 N_1(x). \quad\quad (Eq-2) \end{equation} Les relations (Eq-1) et (Eq-2) impliquent que les deux normes $N_1$ et $N_2$ sont équivalentes.
Soit $E=\R_n[X]$ muni de la norme suivante $\norme{P}=\sup\{\abs{P(t)},\,t\in [0,1]\}.$ Montrer la relation suivante: $$\exists c>0,\quad \forall P\in E,\, \abs{P(2019)+P(2020)} \leq c\int_0^1 \abs{P(t)}\ud t.$$
L'application $\fonct{\varphi}{E}{\R}{P}{P(2019)+P(2020)}$ est linéaire donc continue puisque $E$ est de dimension finie. D'après la caractérisation des applications linéaires continues, il existe $K>0$, tel que pour tout $P\in E$, on a $\abs{\varphi(P)}\leq K\norme{P}$. D'autre part, l'application qui à $P$ associé $\dsp\int_0^1\abs{P}$ définie une norme sur $E$ donc équivalente à la norme déjà définie. On en déduit alors $$\exists \alpha>0,\quad \forall P\in E,\quad \norme{P}\leq \alpha \int_0^1\abs{P(t)}\ud t.$$ Il suffit alors de prendre $c=\alpha \times K$.
Soient $\Omega=\{\begin{pmatrix} a&c\\b&d \end{pmatrix}\in \MM_2(\R),\, (a-d)^2+4bc>0\}$ et $F=\{\begin{pmatrix} a&c\\b&d \end{pmatrix}\in \MM_2(\R),\, (a-d)^2+4bc\geq 0\}$. Montrer que $\Omega$ est un ouvert de $\MM_2(\R)$ et $F$ est un fermé de $\MM_2(\R)$.
On définie la fonction $f$ de $\MM_2(\R)$ dans $\R$ par $f(A)= (a-d)^2+4bc$ si $A=\begin{pmatrix} a&c\\b&d \end{pmatrix}$. $f$ est une fonction polynomiale en les cordonnées de $A$ donc $f$ est continue sur $\MM_2(\R)$. Il suffit après d'écrire $\Omega=f^{-1}(\R_+^*)$ et $F=f^{-1}(\R_+)$.
- Soit $f$ continue sur [0,1], à valeurs dans [0,1]. Montrer qu'il existe $c$ appartenant à [0,1] tel que $f(c)=c$.
- Soient $f$ et $g$, continues sur [0,1], à valeurs dans $[0,1]$, telles que $ f \circ g = g \circ f$. Montrer qu'il existe $x$ appartenant à [0,1] tel que $f(x)=g(x)$.
- On pose, pour $x\in [0,1],\,\,g(x)=f(x)-x$, alors $g\in \CC([0,1])$ de plus $g(0)=f(0)\geq 1$ et $g(1)=f(1)-1\leq 0$ donc $g(1)g(0)\leq 0$, on en déduit d'après le TVI qu'il existe $c\in [0,1]$ tel que $g(c)=0$ soit $f(c)=c$.
- Supposons que, pour tout $x\in [0,1]$, $f(x)>g(x)$ alors il existe $\beta>0$ tel que $f\geq \beta +g$. Ce qui donne: $$\forall x\in [0,1],\,\,f^2(x)=f(f(x))\geq g(f(x))+\beta =f(g(x))+\beta\geq g(g(x))+2\beta =g^2(x)+2\beta ,$$ puis on montre par récurrence sur $n\in \N^*$, que $f^n(x)\geq g^n(x)+n\beta$. Or $1\geq f^n(x)-g^n(x)\geq n\beta$ ce qui est impossible. De même en échangeant les rôles entre $f$ et $g$, on trouve que l'hypothèse $g>f$ est impossible. On en déduit qu'il existe $c\in [0,1]$ tel que $f(c)=g(c)$.
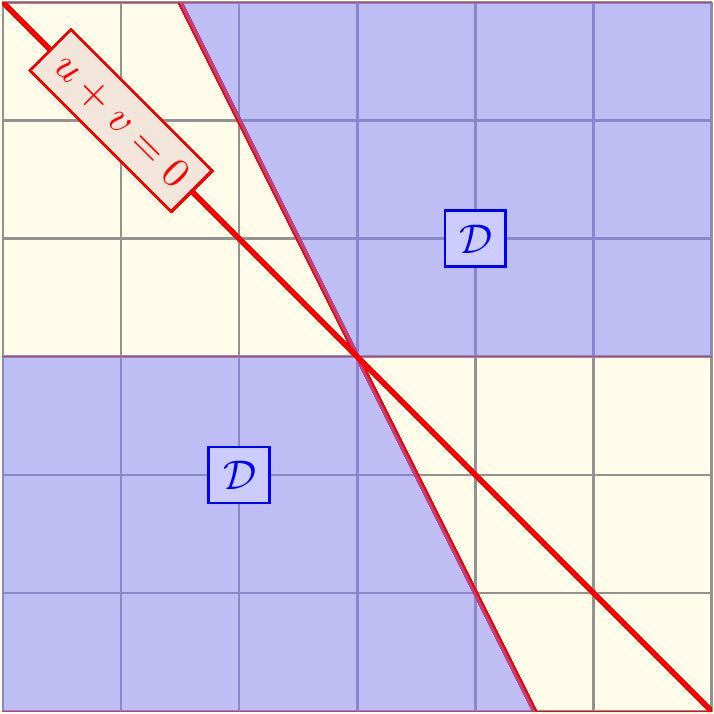
Soit l'application $\fonct{G}{\R^2}{\R^2}{ (u,v)}{(\frac{u}{u+v},\frac{\sqrt{v(v+2u)}}{u+v})}$. On note $\mathcal{D}$ l'ensemble de définition de $G$. Déterminer $G(\mathcal{D})$. $G$ est-elle continue sur $\mathcal{D}$?
Déterminons d'abord le domaine de définition de $f$. $f$ est définie pour $(u,v)\in \R^2$ tels que : $u+v\neq 0$ ET $v(v+2u)\geq 0$.
Soit $(u,v)\in \mathcal{D}$, on a: $$ \left(\dfrac{u}{u+v}\right)^2 + \left(\dfrac{\sqrt{v(v+2u)}}{u+v}\right)^2=\dfrac{u^2+v(v+2u)}{(u+v)^2}=\dfrac{(u+v)^2}{(u+v)^2}=1.$$ On en déduit alors que $G(\mathcal{D})\subset \CC=\{(x,y)\in \R^2,\,x^2+y^2=1\}$.
Inversement, soit $(x,y)\in \CC$,
- Si $x\neq 0$ et $xy\geq 0$, on pose $$u =1,\, v=-1+\dfrac{1}{x},\,\, u+v=\dfrac{1}{x}\neq 0,\, v(v+2u)=(-1+\dfrac{1}{x})(1+\dfrac{1}{x})=-1+\dfrac{1}{x^2}=\dfrac{y^2}{x^2}>0$$ donc $(u,v)\in \mathcal{D}$, de plus; $$F(u,v)=\left(\dfrac{1}{1-1+\dfrac{1}{x}}, \dfrac{\sqrt{(-1+\dfrac{1}{x})(1+\dfrac{1}{x})}}{1-1+\dfrac{1}{x}}\right) = (x,x\dfrac{\abs{y}}{\abs{x}})=(x,x\dfrac{y}{x})=(x,y) $$ donc $(x,y)\in G(\mathcal{D})$
- Si $x\neq 0$ et $xy\leq 0$, on pose $$u =-1,\, v=1-\dfrac{1}{x},\,\, u+v=\dfrac{-1}{x}\neq 0,\, v(v+2u)=(1-\dfrac{1}{x})(-1-\dfrac{1}{x})=-1+\dfrac{1}{x^2}=\dfrac{y^2}{x^2}>0$$ donc $(u,v)\in \mathcal{D}$, et on vérifie que $$F(u,v)=\left(\dfrac{-1}{1-1-\dfrac{1}{x}}, \dfrac{\sqrt{(-1-\dfrac{1}{x})(1-\dfrac{1}{x})}}{1-1+\dfrac{-1}{x}}\right) =(x,-x\dfrac{\abs{y}}{\abs{x}})=(x,-x\dfrac{-y}{x})=(x,y) $$ donc $(x,y)\in G(\mathcal{D})$
- Le cas $x=0,\, y=\mp 1$ ne pose aucun problème (puisque $(0,1)=G(0,1),\,(0,-1)=G(0,-1)$)
On en déduit alors que $G(\mathcal{D})=\CC$.
- Soient $E$ est un espace vectoriel normé de dimension finie, $f : E \longmapsto \R$ une application continue et $a\in \R$. Dire si les ensembles suivants sont ouverts ou fermés : $$A=\{x \in E\mid f (x) = a\}, B=\{x \in E \mid f (x) \leq a\}, C = \{x \in E \mid f (x) < a\}.$$
- Montrer que $GL_n (\K)$ est ouvert dans $\MM_n (\K)$ .
- Soit $f$ une fonction continue de $\R$ dans $\R$. Montrer que son graphe $G = \{(x, f (x)) \mid x \in \R\}$ est fermé dans $\R^2$.
- $A=f^{-1}(\{a\})$ donc $A$ est un fermé, $B=f^{-1}(]-\infty,a])$ donc $B$ aussi est un fermé. En revanche, $C=f^{-1}(]-\infty,a[)$ donc $C$ est un ensemble ouvert.
-
L'application $\fonct{\det}{\MM_n(\R)}{\R}{A}{\det(A)}$ est une fonction continue, puisqu'il
s'agit d'une
fonction polynomiale en les coordonnées de $A$ (mais aussi une application $n$-linéaire donc
continue).
On sait que $GL_n(\R)=\det^{-1}(\R^*)$ donc $GL_n(\R)$ est un ensemble ouvert. -
On définit sur $\R^2$ la fonction $\varphi$ par $\varphi (x,y)=y-f(x)$. $\varphi$ est
continue sur $\R^2$ comme la somme de deux fonctions continues, et on a
$G=\varphi^{-1}(\{0\})$ donc $G$ est un fermé de $\R^2$.
Remarque: On aurait pu aussi utiliser la caractérisation séquentielle de la continuité. En effet, si $((x_n,y_n))_n$ une suite d'éléments de $G$ qui converge dans $\R^2$, alors $x_n\tendversN\, x$ puis $y_n=f(x_n)$ (puisque $(x_n,y_n)\in G$) converge vers $f(x)$ puisque $f$ est continue. Ainsi la limite de la suite $((x_n,y_n))_n$ est dans $G$ ce qui prouve que $G$ est un fermé.
Soient $E$ un espace vectoriel normé et $A$ une partie non vide de $E$. Pour $x \in E$, on pose $$\ud(x,A) = \inf \left\{ \norme{x - a},\,\,a \in A \right\}$$ Montrer que l'application $x \mapsto \ud(x,A)$ est définie et continue sur $E$.
L'application $\ud$ est bien définie (c.f. cours). Soient $x,y\in E$, on a $$\forall z\in A,~\ud(x,A)\leq \norme{x-z}\leq \norme{x-y}+\norme{y-z}$$ donc $$\forall z\in A,~~\ud(x,A)- \norme{x-y}\leq \norme{y-z}\Longrightarrow \ud(x,A)- \norme{x-y}\leq \ud(y,A)$$ En échangeant les rôles entre $x$ et $y$, on trouve $$d(y,A)- \norme{y-x}\leq d(x,A)\Longrightarrow \boxed{\abs{\ud (x,A)-\ud (y,A)}\leq \norme{x-y}}.$$ Donc l'application $\ud $ est $1$- lipschitzienne. On en déduit alors que $x \mapsto \ud(x,A)$ est continue.
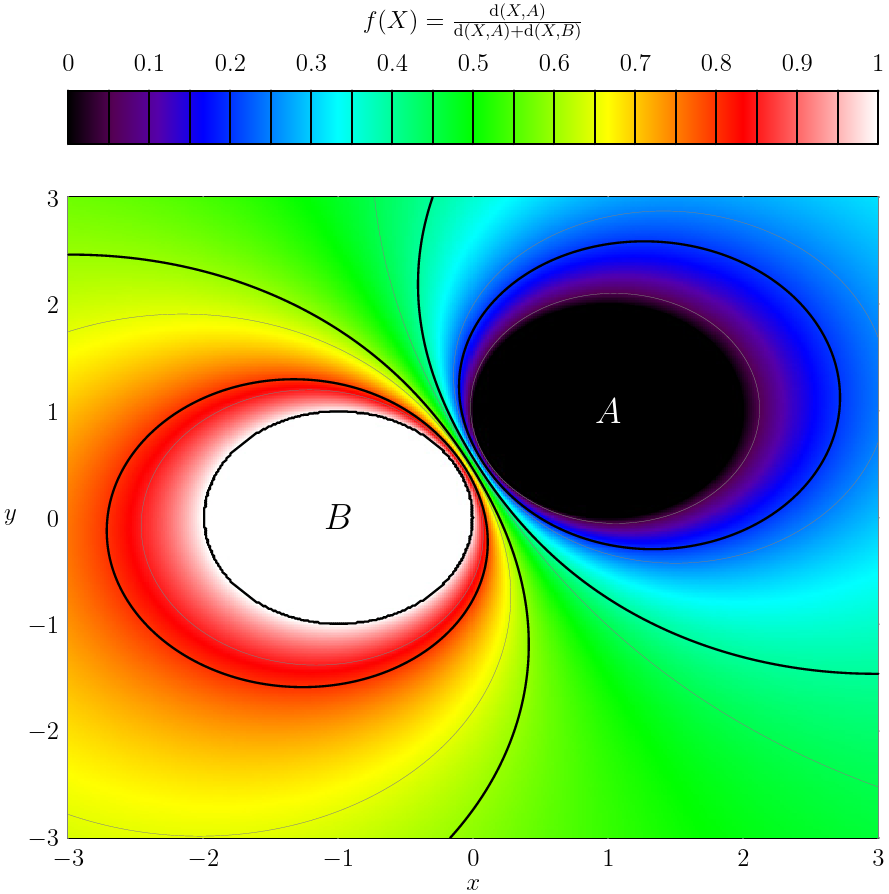
Soit $E$ un evn
- Soient $A,\,B$ deux fermés non vides de $E$. Montrer que: $$A\cap B =\emptyset \Longleftrightarrow \forall x\in E,\quad \ud (x,A)+\ud (x,B)\neq 0.$$
- On suppose que $A\cap B=\emptyset$. Construire une application $f$ continue de $E$ dans $\R$ telle que $f_{\mid A}=0$ et $f_{\mid B}=1$. En déduire l'existence de deux ouverts disjoints $U$ et $V$ tels que $A\subset U$ et $B\subset V$.
- On sait que $\ud (x,A)=0\Leftrightarrow x\in \overline{A}$, puisque $A$ et $B$ sont fermés alors $\overline{A}=A$ et $\overline{B}=B$. Donc en utilisant la première remarque, on a: $$\begin{array}{lcl} \ud (x,A)+\ud (x,B)=0&\Longleftrightarrow & \ud (x,A)=0=\ud (x,B)\\ &\Longleftrightarrow & x\in A \text{ et }x\in B\\ & \Longleftrightarrow & x\in A\cap B \end{array}$$ On en déduit donc, $A\cap B=\emptyset$ ssi pour tout $x\in E,\quad \ud (x,A)+\ud (x,B)>0$.
- On définit $f$ par, $$\forall x\in E,\,\,f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}.$$ $f$ est bien définie puisque $\ud (x,B)+\ud (x,A)>0$. De plus $f$ est continue sur $E$, puisque $x\mapsto \ud(x,A)$ (resp. $x\longmapsto \ud(x,B)$) sont continues sur $E$. D'autre part, on a: $$\forall x\in A,\quad f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}=\dfrac{0}{\ud (x,B)}=0,$$ $$ \forall x\in B,\quad f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}=\dfrac{\ud (x,A)}{\ud (x,A)}=1.$$
Posons maintenant $U=f^{-1}(]-\infty,\frac{1}{2}[),\,\, V=f^{-1}(]\frac{1}{2},\infty[)$, comme $f$ est continue on a $U,\,V$ sont des ouverts de $E$ et clairement $U\cap V=\emptyset$ et $A\subset U,\,\,B\subset V$.
Soient $E$ un $\R$-evn de dimension finie et $F$ une partie bornée non vide de $E$. On définie $\delta (F)=\underset{x,\,y\in F}{\sup}\norme{x-y}$.
- Montrer que $\delta (F)$ est bien définie.
- Peut-on avoir $\delta(F)=0$?
- On suppose de plus que $F$ est fermé et $F$ n'est pas un singleton. Montrer qu'il existe $(x_0,y_0)\in F^2$ tel que $\delta (F)=\norme{x_0-y_0}$, puis montrer que $x_0,\,y_0$ ne sont pas dans $\overset{\circ}{F}$.
- Notons $A=\{\norme{x-y},\,x,y\in F\}\subset \R$, $A$ n'est pas vide car $F\neq \emptyset$, de plus $A$ est borné, en effet comme $F$ est borné, alors $$\exists M>0,\,\forall z\in F,\,\norme{z}\leq M\Longrightarrow \forall x,y\in F,\quad \norme{x-y}\leq \norme{x}+\norme{y}\leq 2M.$$ Ainsi, $A$ admet une borne supérieur, autrement dit, $\delta (F)$ est bien définie.
-
Si $F$ contient au moins 2 éléments $x\neq y$ alors
$\delta (F)>\norme{x-y}>0$.
Donc $\delta (F)=0$ ssi $F$ ne contient qu'un seul élément. -
Considérons la fonction $\fonct{\varphi}{F\times F}{\R}{(x,y)}{\norme{x-y}}$.
$\varphi$ est continue sur $F^2$, de plus $F^2$ est un fermé borné de $E^2$,
donc d'après le cours $\varphi$ est borné sur $F^2$ et atteint ses bornes.
Ainsi, il existe $(x_0,y_0)\in F^2$ tel que $\varphi (x_0,y_0)=\dsp\sup_{F^2}\varphi=\delta (F)$.
Supposons que $x_0\in\overset{\circ}{F}$ alors il existe $r>0$ tel que $B(x_0,r)\subset F$. On pose alors $z_0=x_0+\dfrac{r}{2}(x_0-y_0)$ de sorte que $z_0\in B(x_0,r)$ donc $z_0\in F$, puis $$\varphi(z_0,y_0)=\norme{x_0+\dfrac{r}{2}(x_0-y_0)-y_0}=\left(1+\dfrac{r}{2}\right)\norme{x_0-y_0}>\varphi(x_0,y_0)$$ ce qui est absurde, donc $x_0\not\in \overset{\circ}{F}$.
De même on montre que $y_0\not\in \overset{\circ}{F}$.
Soit $E$ un $\R$-espace vectoriel de dimension finie, $K$ un fermé borné de $E$ et $f:K\to K$ vérifiant : $$ \forall x,y\in K,~~~~(x\not = y\Longrightarrow \norme{f(x)-f(y)}< \norme{x-y}).$$
- Montrer que $f$ est continue sur $K$.
- Montrer que $f$ admet un point fixe et un seul sur $K$. (On pourra considérer $g:K\to \R,x\mapsto \norme{f(x)-x}$.)
- L'application $f$ est $1$- lipschitzienne donc $f$ est continue sur $K$.
- On définit $\fonct{g}{K}{\R_+}{x}{\norme{f(x)-x}}$. La fonction $g$ est continue sur un fermé bornée à valeur dans $\R_+$ donc elle atteint ses bornes ( cours), donc $$\exists \ell\in K,\, g(\ell)=\norme{f(\ell)-\ell}=\underset{x\in K}{\min}(g(x)).$$ Montrons que $g(\ell)=0$ (ce qui donne $f(\ell)=\ell$). Pour cela, on va raisonner par l'absurde, supposons que $g(\ell)>0$, alors d'après la définition de $\ell$, on a $$0< \norme{f(\ell)-\ell}=g(\ell)\leq g(f(\ell))=\norme{f(f(\ell))-f(\ell)}< \norme{f(\ell)-\ell}\Longrightarrow \norme{f(\ell)-\ell}< \norme{f(\ell)-\ell},$$ ce qui est impossible donc $g(\ell)=0$ soit $\ell$ un point fixe de $f$. Il reste à montrer l'unicité de $\ell$, supposons qu'il existe un autre point fixe $\ell'$ de $f$ avec $\ell\neq \ell'$, alors $$0< \norme{\ell-\ell'}=\norme{f(\ell)-f(\ell')}< \norme{\ell-\ell'} \Longrightarrow \text{contradiction}.$$ Donc $\ell$ est le seul point fixe de $f$.
Soit $f$ la fonction définie sur $\R^2$ par: $$\forall x\in \R^*,y\in \R,\quad f(x,y)=\dfrac{\sin(xy)}{x}, \text{ et }, \forall y\in \R,\quad f(0,y)=y.$$ Étudier la continuité de $f$.
On définit sur $\R$ la fonction $\varphi$ par, $$\forall t\neq 0, \quad \varphi(t)=\dfrac{\sin(t)}{t},\text{ et } \varphi(0)=1.$$ Il est clair que $\varphi\in \CC(\R^*)$, de plus comme $\dfrac{\sin(t)}{t}\tendvers{t}{0}1$, on en déduit que $\varphi\in \CC(\R)$.
On remarque que, pour tout $(x,y)\in \R^2,\, f(x,y)=y\varphi(xy)$. On en déduit alors que $f\in \CC(\R^2,\R)$ comme produit et composition des fonctions continues.
Soit $f\in \CC(\R)$. On définit la fonction $g$ sur $\R^*\times \R$ par: $$\dsp\forall (x,y)\in \R^*\times \R,~~~~g(x,y)=\dfrac{1}{x}\int_x^{xy}f(t)\ud t.$$ Montrer que la fonction $g$ peut se prolonger par continuité sur $\R^2$.
Comme $f$ est continue sur $\R$, alors $f$ admet une primitive sur $\R$, qu'on note $F$ ($F\in \CC^1(\R,\R)$ et $F'=f$). On note aussi $\fonct{p_1}{\R^2}{\R}{(x,y)}{x}$ et $\fonct{p_2}{\R^2}{\R}{(x,y)}{y}$. Il est clair que $p_1, p_2$ sont continues sur $D$, de plus $p_1$ ne s'annule pas sur $D$ donc $1/p_1$ est aussi continue sur $D$. On peut alors écrire $g=\dfrac{F\circ (p_1p_2)-F\circ p_1}{p_1}$, ceci prouve que $g$ est continue sur $D$. D'autre par, pour tout $x\neq 0$ et $y\neq 0$, on a $$\begin{array}{lcl} g(x,y)&=&\dfrac{F(yx)-F(x)}{x}=\dfrac{F(yx)-F(0)+F(0)-F(x)}{x-0}\\ &&\\ &=&y\dfrac{F(yx)-F(0)}{yx-0}-\dfrac{F(x)-F(0)}{x-0}\tendvers{x}{0}yF'(0)-F'(0) \end{array}$$ Comme $F'(0)=f(0)$, alors $g(x,y)\tendvers{x}{0} (y-1)f(0)$. Ce résultat reste vrai si $y=0$ puisque $$g(x,0)=\dfrac{-1}{x}\dsp\int_0^xf(t)\ud t\tendvers{x}{0}-f(0).$$ On en déduit qu'on peut prolonger $g$ par continuité sur $\R^2$, on posant $g(0,y)=(y-1)f(0)$.
Déterminer toutes les applications $f$ dans chacun des cas suivants:
- $f:\R\to\R$, $f$ continue et $\forall x\in \R\ , \ f(2x+1)=f(x)$.
- $f:\R\to\R$, $f$ continue et $\forall x,y\in \R\ , \ f(x+y)=f(x)+f(y)+xy$.
- $f:\R_+^*\to\R$, $f$ continue et $\forall x,y\in \R_+^*\ , \ f(xy)=xf(y)+yf(x)$.
- $f:\R\to\R$ , $f$ continue et $\forall x,y\in \R\ , \, f\left(\dfrac{x+y}{2}\right)=\dfrac12\left(f(x)+f(y)\right)$.
- Soit $x\in \R$, on a $$\begin{array}{lcl} f(x)&=&f\left(2\left(\frac{x}{2}-\frac{1}{2}\right)+1\right)= f\left(\frac{x}{2}-\frac{1}{2}\right)\\ &&\\ &=& f\left(2\left(\frac{x}{4}-\frac{1}{4}-\frac{1}{2}\right)+1\right)=f\left(\frac{x}{4}-\frac{1}{2}-\frac{1}{4}\right)\\ &&\\ &=&f\left(\frac{x}{4}-\frac{3}{4}\right). \end{array}$$ Puis, on montre par récurrence sur $n\in \N$, que pour tout $n\in \N,\quad f(x)=f\left(\frac{x}{2^n}-\frac{2^n-1}{2^n}\right)$. Comme $f$ est continue, et la suite $\left(\frac{x}{2^n}-\frac{2^n-1}{2^n}\right)_{n\in \N}$ converge dans $\R$, alors $$f(x)=\limiteX{n}{\infty}f\left(\frac{x}{2^n}-\frac{2^n-1}{2^n}\right)=f\left(\limiteX{n}{\infty}\left(\frac{x}{2^n}-\frac{2^n-1}{2^n}\right)\right)=f(-1) ,$$ car $\dsp \frac{x}{2^n}-\frac{2^n-1}{2^n}\tendversN -1$. On en déduit alors que $f$ est une fonction constante. Inversement, si $f$ est constante alors $f$ vérifie la condition $f(2x+1)=f(x)$.
-
Soit $f$ une fonction continue vérifiant la condition $f(x+y)=f(x)+f(y)+xy$. Alors, on a
$f(0)=2f(0)+0$ ce qui donne $f(0)=0$, puis
$$f(2)=f(1)+f(1)+1=2f(1)+1,\quad f(3)=f(2+1)=3f(1)+3,$$
$$f(4)=f(2+2)=4f(1)+7,\quad f(5)=f(3+2)=5f(1)+10,\cdots.$$
On montre alors que, pour tout $n\in \N,\quad f(n)=nf(1)+\dfrac{n(n-1)}{2}$ (démonstration
par récurrence).
Ensuite, pour $q\in \N^*$, on a
$$\begin{array}{lcl}
f(1)&=&f\left(\frac{q}{q}\right)=f\left(\frac{q-1}{q}+\frac{1}{q}\right)=f\left(\frac{q-1}{q}\right)+f\left(\frac{1}{q}\right)+\dfrac{q-1}{q^2}\\
&=&f\left(\frac{q-2}{q}\right)+f\left(\frac{1}{q}\right)+\dfrac{q-2}{q^2}+f\left(\frac{1}{q}\right)+\dfrac{q-1}{q^2}\\
&=&f\left(\frac{q-2}{q}\right)+2f\left(\frac{1}{q}\right)+\dfrac{q-2}{q^2}+\dfrac{q-1}{q^2}\\
&=&\cdots
=f(0)+qf\left(\frac{1}{q}\right)+\dfrac{1+2\cdots+(q-1)}{q^2}=qf\left(\frac{1}{q}\right)+\dfrac{q(q-1)}{2q^2}
\end{array}$$
Ce qui donne,
$f\left(\frac{1}{q}\right)=\frac{1}{q}f(1)+\frac{1}{2}\frac{1}{q}\left(\frac{1}{q}-1\right)$.
On montre après que pour tout $q\in \N^*$ et $p\in \N$,
$f\left(\frac{p}{q}\right)=pf\left(\frac{1}{q}\right)+\frac{p(p-1)}{2q^2}$.
On en déduit finalement que $f$ sur $\Q_+$ est de la forme $f(x)=xf(1)+\frac{x(x-1)}{2}$,
ensuite par densité de
$\Q_+$ dans $\R_+$ et vu que $f$ est continue, on trouve que $f$ est de la forme
$f(x)=\frac{x^2}{2}+\alpha x,\,\alpha\in \R$.
Pour $x\in \R_-$, on a $0=f(x-x)=f(x)+f(-x)-x^2$ donc $f(x)=x^2-f(-x)=\frac{x^2}{2}+\alpha x$. Inversement, si $f$ est définie par $f(x)=x^2/2+\alpha x$ on vérifie facilement que $f$ est une solution de l'équation. On en déduit que l'ensemble de solution est $\{f(x)=\frac{x^2}{2}+ax,\,\,a\in \R\}$. - On pose $g(z)=\frac{f(z)}{z}$, $g$ vérifie: $$\forall x,y>0,\, g(xy)=g(x)+g(y),$$ comme $g$ est continue, on a $g(x)=k\ln(x)$ (avec $k\in \R$). On en déduit que $f(x)=kx\ln(x)$.
-
Soit $f$ une fonction vérifiant la relation, alors $g=f-f(0)$ vérifie également la même
relation mais avec
$g(0)=0$.
Pour $x\in \R$, on a $2g(x/2)=g(x)$ puis pour $x,y\in R$, on a $g(\frac{x+y}{2})=\frac{1}{2}(g(x)+g(y))=g(x/2)+g(y/2)$. Donc $g$ est de la forme $g(x)=\lambda x$ avec $\lambda\in \R$.
Soit $\varphi:\,(\MM_n(\R)\setminus\{0\})^2\mapsto\R$ définie par $\varphi(A,B)=\dfrac{\norme{AB}_1}{\norme{A}_1\norme{B}_1}$. Montrer que $\varphi$ est continue, bornée puis trouver $\sup\varphi$.
Même question avec $g(A,B)=\dfrac{\norme{AB}_2}{\norme{A}_2\norme{B}_2}$ et $h(A,B)=\dfrac{\norme{AB}_\infty}{\norme{A}_\infty\norme{B}_\infty}$.
L'application $\psi :(A,B)\in \MM_n(\R)^2\longmapsto AB $ est continue sur $\MM_n(\R)$ car $\psi$ est bilinéaire.
L'application $N:A\in \MM_n(\R)\setminus\{0\}\longmapsto \norme{A}_1$ est continue sur $\MM_n(\R)\setminus\{0\}$ (1-Lipschitzienne), de plus
ne s'annule pas sur $\MM_n(\R)\setminus\{0\}$.
L'application $\varphi$ est donc continue comme composé et produit des fonctions continues ($\varphi(A,B) =
N(\psi(A,B))/(N(A)\times N(B))$).
Soient $A=(a_{i\,j}), \, B=(b_{i\,j})$ deux matrices non nulles, on a $$\forall (i,j)\in \inter{1,n}^2,\, (AB)_{i\,j}=c_{i\,j}=\dsum_{k=1}^n a_{i\,k}b_{k,j} \longrightarrow \abs{c_{i\,j}}\leq \dsum_{k=1}^n \abs{a_{i\,k}}\abs{b_{k,j}}.$$ Notons, pour $i\in \inter{1,n},\, L_i(A)=\dsum_{k=1}^n\abs{a_{i\,k}}$, On en déduit alors $$\forall (i,j)\in \inter{1,n}^2,\, \abs{c_{i\,j}}\leq L_i(A)\dsum_{k=1}^n \abs{b_{k,j}}$$ donc, $$ \norme{AB}_1\leq \dsum_{i=1}^n \dsum_{j=1}^n\left(L_i(A) \dsum_{k=1}^n\abs{b_{k\,j}}\right) = \dsum_{i=1}^n \left(L_i(A) \dsum_{j=1}^n\dsum_{k=1}^n\abs{b_{k\,j}}\right)=\norme{B}_1\dsum_i L_i(A)=\norme{B}_1\norme{A}_1.$$ Donc $\varphi(A,B)\leq 1$, ceci prouve que $\varphi$ est bornée et $\sup\varphi \leq 1$.
On pose $A=E_{1\,1}$ la matrice dont tous les coefficients sont nuls sauf $a_{1\,1}=1$, on a $$A\neq 0,\,\,\norme{A}_1=1,\,\, A^2=A,\quad \varphi(A,A)=\dfrac{\norme{A^2}_1}{\norme{A}_1^2}=\dfrac{1}{1}=1 $$ donc $\sup\varphi \geq 1$. On en déduit alors que $\boxed{\sup\varphi =1 }$.
Pour la fonction $g$, soient $A=(a_{i\,j}), \, B=(b_{i\,j})$ deux matrices non nulles, on a $$ \begin{array}{lcl} \norme{AB}_2^2&=&\dsp \dsum_{1\leq i,j\leq n}\left(\dsum_{k=1}^n a_{i\,k}b_{k\,j}\right)^2\\ &&\\ &\leq & \dsp \dsum_{1\leq i,j\leq n}\left(\dsum_{\alpha =1}^n a_{i\,\alpha}^2\right)^2\left(\dsum_{\beta =1}^nb_{\beta \,j}^2\right) \quad (\text{Cauchy-Schwarz})\\ &&\\ &=&\dsum_{1\leq i,j\leq n}\dsum_{1\leq \alpha ,\beta\leq n} a_{i\,\alpha}^2 b_{\beta\,j}^2= \left( \dsum_{1\leq i,\alpha \leq n} a_{i\,\alpha}^2\right) \left( \dsum_{1\leq \beta ,j \leq n} b_{\beta\,j}^2\right) \\ &=& \norme{A}_2^2\norme{B}_2^2. \end{array} $$ Donc $g(A,B)\leq 1$, ceci prouve que $g$ est bornée et $\sup g\leq 1$. D'autre part, en considérant le même exemple $A=E_{1\,1}$ on trouve $\boxed{\sup g =1 }$.
Pour la fonction $h$, l'estimation est plus simple. $$ \norme{AB}_\infty =\max_{1\leq i,j\leq n}\abs{\dsum_{k=1}^na_{i\,k}b_{k\,j}}\leq \max_{1\leq i,j\leq n}\dsum_{k=1}^n\abs{a_{i\,k}}\abs{b_{k\,j}} \leq \max_{1\leq i,j\leq n}\dsum_{k=1}^n\norme{A}_\infty\norme{B}_\infty =n\norme{A}_\infty\norme{B}_\infty. $$ Donc $h(A,B)\leq n$, ceci prouve que $h$ est bornée et $\sup g\leq n$.
considérons la matrice $J$ dont tous les coefficients sont égaux à $1$, on a $$J\neq 0,\, \norme{J}_\infty =1,\,\, J^2=nJ,\quad h(J,J)=\dfrac{\norme{J^2}_\infty}{\norme{J}_\infty^2}=\dfrac{n}{1}=n. $$ On en déduit alors $\boxed{\sup h =n }$.
Soit $(E,\norme{\cdot})$ un EVN. On définit l'application $f$ sur $E$ par $f(x)=\dfrac{x}{1+\norme{x}^2}$ pour tout $x\in E$.
- Montrer que $f$ est continue de $(E,\norme{\cdot})$ dans $(E,\norme{\cdot})$.
- Montrer que $f(E)=\overline{B}(0,\frac{1}{2})$.
- $f$ est la somme produit des fonctions continues
-
Pour tout $x\in E$, $\norme{f(x)}=\dfrac{\norme{x}}{1+\norme{x}^2}$. Une étude rapide de la
fonction $t\longmapsto\dfrac{t}{1+t^2}$, montre que,
$$\forall t\in \R,\,\abs{\dfrac{t}{1+t^2}}\leq \dfrac{1}{2} \Longrightarrow \forall x\in
E,\,f(x)\in \overline{B}(0,\frac{1}{2})$$
ceci montre que $f(E)\subset \overline{B}(0,\frac{1}{2})$.
Inversement, soit $y\in \overline{B}(0,\frac{1}{2})$ non nul. On pose, $x=\dfrac{1+\sqrt{1-4\norme{y}^2}}{2\norme{y}^2}y$, alors $$f(x)=\dfrac{\dfrac{1+\sqrt{1-4\norme{y}^2}}{2\norme{y}^2}y }{1+\norme{\dfrac{1+\sqrt{1-4\norme{y}^2}}{2\norme{y}^2}y}^2}=\dfrac{2(1+\sqrt{1-4\norme{y}^2})}{4\norme{y}^2+(1+\sqrt{1-4\norme{y}^2})^2}y=\dfrac{2(1+\sqrt{1-4\norme{y}^2})}{2+2\sqrt{1-4\norme{y}^2}}y=y$$ ceci prouve que $y\in f(E)$, donc $\overline{B}(0,\frac{1}{2})\subset f(E)$ d'où l'égalité.
Soient $(E,\norme{\cdot})$ un EVN et $a\in E$ non nul, on considère l'application $f$ définie par: $$\forall x\in E,\quad f(x)=\norme{x-a} \text{ si }\norme{x}\leq \norme{a}, \text{ et } f(x)=0 \text{ sinon }.$$
- Montrer que $f$ est continue en $a$.
- Montrer que $f$ n'est pas continue en $-a$.
-
Il est clair que $f(a)=0$.
Soit $(x_n)$ une suite d'éléments de $E$ qui converge vers $a$, donc
$$\forall \varepsilon>0,\,\exists n_0,\,\forall n\geq n_0,\,\norme{x_n-a}\leq \varepsilon.$$
Pour $n\geq n_0$, si $\norme{x_n}>\norme{a}$ alors $f(x_n)=0$, sinon
$f(x_n)=\norme{x_n-a}\leq \varepsilon$.
Dans les deux cas, pour tout $n\geq n_0$, on a $\abs{f(x_n)}\leq \varepsilon$, ce qui prouve que $f(x_n)\tendversN 0=f(a)$.
D'après la caractérisation séquentielle de la continuité, $f$ est continue en $a$. - Pour $n\geq 1$, on définit les deux suites : $ u_n=(-1-\frac{1}{n})a,\, v_n=(-1+\frac{1}{n})a$, il est clair que $u_n\tendversN\,-a$ et $v_n\tendversN\,-a$. D'autre part, on a $$\forall n\in \N,\,\norme{u_n}=(1+\frac{1}{n})\norme{a}> \norme{a}\Longrightarrow f(u_n)=0\tendversN\,0,$$ et $$\forall n\in \N,\,\norme{v_n}=(1-\frac{1}{n})\norme{a}\leq \norme{a}\Longrightarrow f(v_n)=\norme{v_n-a}=(2-\frac{1}{n})\norme{a}\tendversN\, 2\norme{a}$$ les deux limites étant différentes, ceci prouve que $f$ n'est pas continue en $-a$.
Soient $A,\,B$ deux parties d'un EVN de dimension finie, une application $f$ de $A$ dans $B$ est appelée homéomorphisme de $A$ dans $B$ si elle est bijective, continue ainsi que sa réciproque.
- Montrer que $f:x\longmapsto \dfrac{x}{1+\abs{x}}$ est un homéomorphisme de $\R$ dans $]-1,1[$.
- Montrer que tout EVN de dimension finie est homéomorphe à chacune de ses boules ouvertes.
- il est facile de vérifie que $f$ est continue strictement croissante de $\R$ dans $f(\R)=]-1,1[$. L'application réciproque $g(x)=\dfrac{x}{1-\abs{x}}$
-
Soit $a\in E$, $r\in \R_+^*$. On pose, pour $x\in E$, $f(x)=a+r\dfrac{x}{1+\norme{x}}$.
$f$ est continue sur comme la somme et le produit des fonctions continue.
D'autre par, $f(E)=B(a,r)$. En effet,
- Pour tout $x\in E$, $$\norme{f(x)-a}=\norme{r\dfrac{x}{1+\norme{x}}} < r\Longrightarrow f(x)\in B(a,r).$$
- Inversement, si $z\in B(a,r)$ , on pose, $x=\dfrac{z-a}{r-\norme{z-a}}$ alors $$f(x)=a + r\dfrac{\dfrac{z-a}{r-\norme{z-a}}}{1+\dfrac{\norme{z-a}}{r-\norme{z-a}}}=a+r \dfrac{z-a}{(r-\norme{z-a})+\norme{z-a}}=a+z-a=z$$ ce qui prouve que $z\in f(E)$.
$H$, définie par $H(0,0)=0$ et $H(x,y)=\dfrac{x^4y}{(x^4+y^2)\sqrt{x^2+y^2}}$ pour $(x,y)\neq (0,0)$ est-elle continue en $(0,0)$.
Soit $(x,y)\in \R^2\setminus \{(0,0)\}$, si $y=0$ alors $H(x,y)=0\tendvers{(x,0)}{(0,0)}0$.
Sinon, on pose $x=r\cos(\theta),\, y=r\sin(\theta)$ avec $r=\sqrt{x^2+y^2}$ et $\theta\in \R$, $\theta\neq 0[\pi]$. Alors $$H(x,y)=\dfrac{r^5 \cos(\theta)^4\sin(\theta)}{r^3 (r^2\cos(\theta)^4+\sin(\theta)^2)}=$$
Soit $E$ un $\R$-EVN et $A,\,B$ deux parties non vides de $E$. Soit $f$ une fonction définie sur $A\cup B$ dans $\R$ telle que $f_{\mid_A}$ et $f_{\mid_B}$ sont continues.
- On suppose que $A$ et $B$ sont des ouverts de $E$. Montrer que $f$ est continue.
- On suppose que $A$ et $B$ sont des fermés de $E$. Montrer que $f$ est continue.
- Dans le cas générale, peut-on dire que $f$ est continue?
-
Soit $x\in A\cup B$, soit $x\in A$ ou $x\in B$. Supposons que $x\in A$, comme $A$ est un ouvert de $E$ alors
il existe $r>0$ tel que $B(x,r)\subset A$.
Considérons maintenant une suite $(x_n)$ d'élément de $A\cup B$ telle que $x_n\tendversN\,x$, d'après la définition de la convergence d'une suite, $$\exists n_0,\quad \forall n\geq n_0,\quad x_n\in B(x,r).$$ Or $B(x,r)\subset A$ et $f$ est continue sur $A$ donc $f(x_n)\tendversN\,f(x)$ ce qui prouve la continuité de $f$ en $x$. -
SSoient $x\in A\cup B$ et $(x_n)_n$ une suite d'éléments de $A\cup B$ telle que $x_n\tendversN\, x$.
On note $I_A=\{n\in \N,\, x_n\in A\}$ et $I_B=\{n\in \N,\, x_n\in B\}\setminus I_A$, de sorte que
$I_A\cap I_B=\emptyset $ et $I_A\cup I_B=\N$.
Si $I_A$ est fini, alors à partir d'un certain rang, tout les termes de la suite $(x_n)$ sont dans $B$, comme $B$ est fermé alors $\dsp \lim_nx_n =x\in B$, $f$ est continue sur $B$ alors $f(x_n)\tendversN\,f(x)$.
Si $I_B$ est fini, avec le même raisonnement $f(x_n)\tendversN\,f(x)$.
Sinon ($I_A$ et $I_B$ sont infinis) la suite $(x_n)_{n\in I_A}\in A^\N$ converge vers $x$ donc $x\in A$ car $A$ est fermé, $f$ étant continue sur $A$ alors $(f(x_n))_{n\in I_A}$ converge vers $f(x)$, de même la suite $(f(x_n))_{n\in I_B}$ converge vers $f(x)$. Comme $I_A\cup I_B=\N$, on en déduit que $f(x_n)\tendversN\,f(x)$.
Conclusion $f(x_n)\tendversN\,f(x)$ ce qui prouve la continuité de $f$. -
Soit $A=[-1,0]$ et $B=]0,1]$, $f$ définie par $f(x)=0$ si $x\in A$ et $1$ si $x\in B$.
Il est clair que $f_{A}$ est continue, de même pour $f_B$, mais $f$ n'est pas continue sur $A\cup B$.
Soient $f,\,g$ deux fonctions de $\R$ dans $\R$.
- On suppose que $f$ est dérivable sur $\R$. Montrer que $f$ est lipschitzienne sur $\R$ ssi $f'$ est bornée sur $\R$.
- On suppose que $f,\,g$ sont lipschitziennes et bornées sur $\R$. Montrer que $fg$ est lipschitzienne sur $\R$. Ce résultats reste-t-il vrai si les fonctions $f,\,g$ ne sont pas bornées?
- On suppose que $f$ est lipschitzienne sur $\R$. Montrer qu'ils existe $A,\,B\in \R_+$ tels que, pour tout $x\in \R$, $\abs{f(x)}\leq A\abs{x}+B$.
- On suppose que $f$ vérifie la propriété suivante: $$\exists M>0,\,\forall x,y\in \R,\quad 0\leq x-y\leq 1\Longrightarrow \abs{f(x)-f(y)}\leq M\abs{x-y}.$$ Montrer que $f$ est lipschitzienne sur $\R$.
-
Supposons que $f$ lipschitzienne, alors il existe $k>0$ tel que, pour tout $(x,y)\in R^2$, on
a
$\abs{f(x)-f(y)}\leq k\abs{x-y}$.
Soit $x\in \R$, comme $f$ est dérivable en $x$ alors $\dsp\limiteX{h}{0}\dfrac{f(x+h)-f(x)}{h}=f'(x)$ mais on a $$\forall h\neq 0,\quad \abs{\dfrac{f(x+h)-f(x)}{h}}\leq k\Longrightarrow \abs{f'(x)}=\abs{\limiteX{h}{0}\dfrac{f(x+h)-f(x)}{h}}\leq k$$ Ceci prouve que $f'$ est borné sur $\R$ et $\norme{f'}_\infty \leq k$. -
Soit $x,y\in\R$, on a
$$
\begin{array}{lcl}
\abs{f(x)g(x)-f(y)g(y)}&=&\abs{f(x)g(x)-f(x)g(y)+f(x)g(y)-f(y)g(y)} =\abs{f(x)(g(x)-g(y)) +g(y)(f(x)-f(y))}\\
&&\\
&\leq& \abs{f(x)}\abs{g(x)-g(y)}+\abs{g(y)}\abs{f(x)-f(y)}\leq k_g \abs{f(x)}\abs{x-y}+k_f \abs{g(y)}\abs{x-y}\\
&&\\
&\leq & \left(k_g\norme{f}_\infty +k_f\norme{g}_\infty \right) \abs{x-y}
\end{array}
$$
Ce qui prouve que $fg$ est lipschitzienne.
L'hypothèse $f,\,g$ bornées est indispensable, comme le montre l'exemple $f(x)=g(x)=x$. - Supposons que $f$ est lipschitzienne, et soit $x\in \R$, on a $$\abs{f(x)} =\abs{f(x)-f(0)+f(0)}\leq \abs{f(x)-f(0)}+\abs{f(0)} \leq k \abs{x-0}+\abs{f(0)}$$ ce qui donne le résultat avec $A=k$ et $B=\abs{f(0)}$.
- Soient $x,y\in \R$, supposons que $x< y$, on note $K_x=\lfloor x \rfloor,\, K_y =\lfloor y \rfloor$. Ensuite, on écrit: $$f(y)-f(x)=f(y)-f(K_y)+f(K_y)-f(K_x)- (f(x)-f(K_x))=f(y)-f(K_y)+\sum_{j=K_x}^{K_y-1}(f(j+1)-f(j))- (f(x)-f(K_x)).$$ Puis, $$ \begin{array}{lcl} \abs{f(y)-f(x)}&=& \abs{f(y)-f(K_y)+\dsum_{j=K_x}^{K_y-1}(f(j+1)-f(j))- (f(x)-f(K_x))}\\ &&\\ &\leq& \abs{f(y)-f(K_y)}+\dsum_{j=K_x}^{K_y-1}\abs{f(j+1)-f(j)}+\abs{f(x)-f(K_x)}\\ &&\\ &\leq & M \abs{y-K_y}+\dsum_{j=K_x}^{K_y-1}M+M\abs{x-K_x}\\ &&\\ &=& M (y-K_y)+M(K_y-K_x)+M(x-K_x)=M (y-x)=M\abs{y-x} \end{array} $$
Soient $E$ un $\K$-evn et $T:E \to E$ définie par $T(u) = \left\{ { \begin{array}{ll} u & {{\text{si }}\left\| u \right\| \leqslant 1} \\ {\frac{u}{{\left\| u \right\|}}} & {{\text{sinon}}} \\ \end{array} } \right.$. Montrer que $T$ est 2-lipschitzienne.
Soient $u,v\in E$,
- Si $\norme{u}\leq 1$ et $\norme{v}\leq 1$, on a immédiatement $$\norme{T(u)-T(v)}=\norme{u-v}\leq 2\norme{u-v}.$$
- Si $\norme{u}> 1$ et $\norme{v}> 1$, en utilisant le résultat de l'exercice \ref{Ex:InegaliteNorme}, on trouve: $$\norme{T(u)-T(v)}= \norme{\dfrac{u}{\norme{u}}-\dfrac{v}{\norme{v}}}\leq \max(\norme{u},\norme{v})\norme{\dfrac{u}{\norme{u}}-\dfrac{v}{\norme{v}}}\leq 2\norme{u-v}.$$
- Si $\norme{u}\leq 1$ et $\norme{v}>1$, on a alors: $$\begin{array}{lcl} \norme{T(u)-T(v)}&=& \norme{u-\dfrac{v}{\norme{v}}}=\norme{u-v+v-\dfrac{v}{\norme{v}}}\\ &\leq & \norme{u-v}+\norme{\left(1-\frac{1}{\norme{v}}\right)v}=\norme{u-v}+\norme{v}-1\\ &\leq & \norme{u-v}+\norme{v}-\norme{u}\leq 2\norme{u-v} \end{array}$$
- Si $\norme{v}\leq 1$ et $\norme{u}>1$, ce cas est équivalent au cas précédent.
Donc, dans tous les cas, on a: $\norme{T(u)-T(v)}\leq 2\norme{u-v}$ ce qui prouve le résultat.
Soit $(a,b)\in (\R_+)^2$. On considère l'application $\fonct{F}{\R^2}{\R^2}{(x,y)}{(ay,bx)}$. Montrer que $f$ est lipschitzienne.
On munit $\R^2$ de la norme $\norme{(x,y)}=\abs{x}+\abs{y}$. Il est clair que, pour tou $(x,y),\,(u,v)\in \R^2$, $$\begin{array}{lcl} \norme{f((x,y))-f((u,v))}&=&\norme{(a(y-v),b(x-u))} =\abs{a}\abs{y-v}+\abs{b}\abs{x-u}\\ &&\\ &\leq& \max\{\abs{a},\abs{b}\}\norme{(x,y)-(u,v)}. \end{array}$$ Ce qui prouve que $f$ est lipschitzienne.
Soit $f$ une fonction définie sur $\R_+$, $k$-lipschitzienne. On définie la fonction $F$ par $$F(0)=f(0),\quad \text{ et pour } x>0,\, F(x)=\dfrac{1}{x}\int_0^xf(t)\ud t.$$
- Montrer qu'on peut écrire $F(x)=\dsp\int_0^1f(xt)\ud t$.
- En déduire que $F$ est $\frac{k}{2}$-lipschitzienne.
- Si $x>0$, on définit le changement de variable $u=\dfrac{t}{x}$, ce qui donne $\ud t =x\ud u$ $$F(x)=\dfrac{1}{x}\int_0^xf(t)\ud t=\dfrac{1}{x}\int_0^1f(xu)(x\ud u)=\int_0^1f(xu)\ud u$$ Cette relation reste vrai pour $x=0$, puisque $F(0)=f(0)=\dsp\int_0^1f(0)\ud u$.
- Soient $x,y\in \R_+$, on a $$\abs{F(x)-F(y)}\leq \int_0^1\abs{f(xu)-f(yu)}\ud u\leq \int_0^1k\abs{xu-yu}\ud u=k\abs{x-y}\int_0^1u\ud u =\dfrac{k}{2}\abs{x-y}.$$
Pour $a\in \R$, pour tout $x\in \R^*$, on pose $f(x)=\dfrac{a+\sin \left(1/x\right)}{x}$. Étudier, en fonction de $a$, les limites à droite et à gauche de $f$ en $0$.
On distingue deux cas:
- $\abs{a}>1$, dans cas pour tout $x\neq 0$, on a $\sin\left(\frac{1}{x}\right)+a$ de même signe que $a$ car $\abs{\sin\left(\frac{1}{x}\right)}\leq 1$, on en déduit alors $$\dfrac{a+\sin \left(1/x\right)}{x}\tendvers{x}{0^+}\,\varepsilon\,\infty,\quad \dfrac{a+\sin \left(1/x\right)}{x}\tendvers{x}{0^-}\,-\varepsilon\,\infty,\quad\text{avec }\varepsilon=\dfrac{a}{\abs{a}}.$$
- $\abs{a}\leq 1$, dans ce cas on n'a pas de limite en $0$. En effet, considérons les deux suites, $$\forall n\geq 1,\quad u_n=\dfrac{1}{-\Arcsin(a)+2\pi n},\,\quad u_n=\dfrac{1}{\Arcsin(a)+2\pi n}. \quad u_n\tendversN\,0,\, v_n\tendversN 0.$$ et on a $f(u_n)=0\tendversN\,0$ et $f(v_n)=(2a)(\Arcsin(a)+2\pi n)\tendversN \,\frac{a}{\abs{a}}\infty$. Donc les deux limites sont différentes. (si $a=0$, on peut prendre $v_n=\dfrac{2}{\pi+4n\pi}$).
Soient $a,\,b\in \R_+^*$. Calculer les limites suivantes: $$\limiteX{x}{0^+}\dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right),\quad \limiteX{x}{0^+}\dfrac{b}{x}\mathrm{E}\left(\frac{x}{a}\right),\quad \limiteX{x}{0^-}\dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right),\quad \limiteX{x}{0^-}\dfrac{b}{x}\mathrm{E}\left(\frac{x}{a}\right).$$
Pour tout $x\in \R^*$, on a: $$\frac{b}{x}\leq \mathrm{E}\left(\frac{b}{x}\right)< \frac{b}{x}+1\Longrightarrow \left\{\begin{array}{lc} \forall x>0,&\frac{b}{a}\leq \dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right) < \frac{b}{a}+\dfrac{x}{a}\\ &\\ \forall x< 0,&\frac{b}{a}+\dfrac{x}{a}< \dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right)\leq \frac{b}{a} \end{array} \right.\Longrightarrow \limiteX{x}{0^+}\dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right)=\limiteX{x}{0^-}\dfrac{x}{a}\mathrm{E}\left(\frac{b}{x}\right)=\dfrac{b}{a}. $$ D'autre part pour $x$ assez proche de $0^+$ on va avoir $x< a$ donc $\mathrm{E}\left(\frac{x}{a}\right)=0$ d'où $\dsp\limiteX{x}{0^+}\dfrac{b}{x}\mathrm{E}\left(\frac{x}{a}\right)=0$. En revanche, pour $x$ proche de $0^-$, on a $\mathrm{E}\left(\frac{x}{a}\right)=-1$ d'où $\dsp\limiteX{x}{0^-}\dfrac{b}{x}\mathrm{E}\left(\frac{x}{a}\right)=\infty$.
- Soit $f:\R \to \R$ une fonction périodique. Montrer que si $f$ admet une limite finie en $+\infty$, alors $f$ est constante.
- Montrer que la fonction $\sin$ n'a pas de limite en $+\infty$.
- Montrer que l'application $\fonct{f}{\R^*}{\R}{x}{\sin\left(\dfrac{1}{x}\right)}$ n'a pas de limite en $0^+$.
- Supposons que $f$ est $T$-périodique avec $T>0$ et $f$ admet une limite $\ell$ en $\infty$. Montrons que $f$ est constante. D'après la caractérisation séquentielle de la limite, pour tout suite $(x_n)$ tel que $x_n\tendversN\,\infty$, on a $f(x_n)\tendversN\,\ell$. Soit maintenant $x\in \R$, on définit la suite $(x_n)$ par $x_n=x+n\times T$, alors $x_n\tendversN\infty$ donc $f(x_n)\tendversN\ell$, or comme $f$ est $T$-périodique on a $f(x_n)=f(x)$, on en déduit que $f(x)=\ell$ ce qui prouve que $f$ est constante.
- Si la fonction $\sin$ admettait une limite en $\infty$ elle serait constante d'après la question précédente (puisque $\sin$ est une fonction périodique). Or la fonction $\sin$ n'est pas constate ( par exemple $\sin(0)=\cdots \neq \cdots =\sin(\pi/2)$. On en déduit alors que limite $\sin$ en $\infty$ n'existe pas.
- Si $x\mapsto \sin(1/x)$ admet une limite en $0^+$ alors en utilisant le résultat sur la composition des limites on aurait $y\mapsto \sin(y)$ admet une limite en $+\infty$. Ce qui n'est pas le cas!
Soient $E$ un $\K$-evn et $A\subset E$ non vide et $a\in E$. Soit $f:A\longmapsto \K$, on suppose que $f$ admet une limite $\beta \neq 0$ en $a$.
- Montrer qu'il existe $r>0$ tel que, pour tout $x\in B=B_f(a,r)\cap A$, on a $f(x)\neq 0$.
- Montrer que $\dfrac{1}{f}$ est bien définie sur $B$ et que $\dfrac{1}{f}$ admet $\dfrac{1}{\beta}$ au point $a$.
- On applique la définition de la limite, avec $\varepsilon =\frac{\abs{\beta}}{2}$, ce qui donne: $$\exists r>0,\quad \forall x\in B_f(a,r)\cap A,\, \abs{f(x)-\beta}\leq \dfrac{\abs{\beta}}{2},$$ or $\abs{\abs{f(x)}-\abs{\beta}}\leq \abs{f(x)-\beta}$, ce qui donne $$\forall x\in B_f(a,r)\cap A,\, \abs{\abs{f(x)}-\abs{\beta}}\leq\abs{f(x)-\beta}\leq \dfrac{\abs{\beta}}{2}\Longrightarrow \forall x\in B_f(a,r)\cap A,\, \dfrac{\abs{\beta}}{2}\leq\abs{f(x)}\leq \dfrac{3\abs{\beta}}{2}.$$ Autrement dit, $\forall x\in B_f(a,r)\cap A,\quad f(x)\neq 0$.
-
Puisque $f$ ne s'annule pas sur $B=B_f(a,r)\cap A$, alors la fonction
$\fonct{g}{B}{\K}{x}{\frac{1}{f(x)}}$
est bien définie.
D'autre part, en utilisant l'hypothèse sur $f$, on a: $$\forall \varepsilon>0, \exists \eta>0,\quad \forall x\in B_f(a,\eta)\cap A,\, \abs{f(x)-\beta}\leq \dfrac{\abs{\beta}^2\varepsilon}{2}.$$ Posons $\alpha=\min (\eta,r)$, on a alors, $$\forall x\in \left(B_f(a,\alpha)\cap A\right)\subset B,\,\abs{g(x)-\dfrac{1}{\beta}}=\abs{\dfrac{\beta -f(x)}{f(x)\beta}}=\dfrac{\abs{f(x)-\beta}}{\abs{\beta}\abs{f(x)}}\leq \dfrac{2\abs{f(x)-\beta}}{\abs{\beta}^2}\leq \varepsilon.$$ Ce qui prouve que $g$ admet une limite en $a$ selon $B$.
Étudier la limite éventuelle en $(0,0)$ de : a) $f(x,y)=\dfrac{x^3+xy^2-2xy}{x^2+y^2}\quad\quad$ b) $g(x,y)=\dfrac{x^4+y^4+2x^2y}{\sqrt{x^2+y^2}}\quad\quad$ c) $h(x,y)=\dfrac{x^3-y^3}{ (x^2+y^2)^{3/2}}$
- Pour $x\in \R^*$, on a $$f(x,x)=\dfrac{2x^3-2x^2}{2x^2}=x-\dfrac{1}{2}\tendvers{x}{0}\dfrac{-1}{2},\quad f(x,0)=\dfrac{x^3}{x^2}=x\tendvers{x}{0}\,0.$$ Les deux limites étant différentes, on en déduit que $f$ n'admet pas de limite en $(0,0)$.
- Pour tout $(x,y)\in \R^2\setminus\{(0,0)\}$, on a: $$\abs{g(x,y)}\leq \dfrac{2\norme{(x,y)}_2^4+2\norme{(x,y)}_2^3}{\norme{(x,y)}_2}\leq 2\norme{(x,y)}_2^3+2\norme{(x,y)}_2^2\tendvers{(x,y)}{(0,0)}\,0.$$ Donc $g$ admet $0$ comme limite en $(0,0)$.
- Pour $x\in \R^*$, on a $$h(x,0)=\dfrac{x^3}{\sqrt{x^2}^3}=\dfrac{x^3}{\abs{x}^3}\Longrightarrow h(x,0)\tendvers{x}{0^+}\,1 \text{ et }h(x,0)\tendvers{x}{0^-}\,-1,$$ donc $h$ n'admet pas de limite en $(0,0)$.
L'application $\fonct{f}{\R^3\setminus \{0\}}{\R^3}{(x,y,z)}{\dfrac{(x,y,z)}{\sqrt{x^2+y^2+z^2}}-(x,y,z)}$ admet-t-elle une limite en $0$?
Rappelons que $\sqrt{x^2}=\abs{x}$...
- [$\triangleright$] Soit $x\in \R_+^*$, on a: $$f(x,x,x)=\dfrac{(x,x,x)}{\sqrt{x^2+x^2+x^2}}-x(1,1,1)=(\dfrac{1}{\sqrt{3}}-x)(1,1,1)\tendvers{x}{0^+}\dfrac{1}{\sqrt{3}}(1,1,1).$$
- [$\triangleright$] Soit $x\in \R_-^*$, on a: $$f(x,x,x)=\dfrac{(x,x,x)}{\sqrt{x^2+x^2+x^2}}-x(1,1,1)=(\dfrac{-1}{\sqrt{3}}-x)(1,1,1)\tendvers{x}{0^-}\dfrac{-1}{\sqrt{3}}(1,1,1).$$
On en déduit que $\dsp\lim_{(x,y,z)\to(0,0,0)} f(x,y,z)$ n'existe pas.
Soit $f \colon \R^2 \setminus \{(0,0)\} \to \R\,$ la fonction définie par: $\dsp f(x,y) = \frac{x^2y^2}{x^2y^2 + (x-y)^2}$. Montrer que $\dsp \lim_{x\to 0}\lim_{y\to 0}f(x,y) = \lim_{y\to 0}\lim_{x\to 0}f(x,y) = 0$, et que $\dsp \lim_{(x,y)\to (0,0)} f(x,y)$ n'existe pas.
On a, pour $x\neq 0$, \[ \lim_{y\to 0}f(x,y) = \lim_{y\to 0}\frac{y^2}{y^2 + (1-y/x)^2} =\dsp\frac{\dsp\lim_{y\to 0} y^2}{\dsp\lim_{y\to 0} y^2 + (1-y/x)^2} =\frac{0}{1} =0, \] donc $\dsp \lim_{x\to 0}\lim_{y\to 0}f(x,y)=0$.
De même $\lim_{y\to 0}\lim_{x\to 0}f(x,y) = 0$ puisque $f(x,y)=f(y,x)$ d'où le résultat. D'autre part, pour $x\neq 0$, $f(x,x) = \dfrac{x^4}{x^4} =1$ d'où $\dsp\lim_{x\to 0}f(x,x) = 1$ et $f(x,2x)=\dfrac{x^4}{5x^4} =4/5$. Donc $\dsp\lim_{(x,y)\to (0,0)} f(x,y)$ ne peut pas exister.
Soit $f : \R^2 \to \R$, définie par $ f(x,y) = \left\{\begin{array}{cc} (x+y)\sin \frac{1}{x} \sin \frac{1}{y} & \text{ si }xy \neq 0 \\ 0 & \text{ si } xy = 0 \end{array}\right .$. Démontrer que les deux limites itérées $\dsp\lim_{x\to 0}\lim_{y\to 0}f(x,y)$ et $\dsp \lim_{y\to 0}\lim_{x\to 0}f(x,y)$ n'existent pas, et que $\dsp \lim_{(x,y)\to (0,0)}f(x,y)$ existe et est égale à $0$.
Soient $x,y\in \R$ tels que $xy\neq 0$, on a $$f(x,y)= x\left(\sin \frac{1}{x} \sin \frac{1}{y}\right) +y\left(\sin \frac{1}{x} \sin \frac{1}{y}\right) =xb(x,y)+yb(x,y),\,\text{ avec } b(x,y)=\sin \frac{1}{x} \sin \frac{1}{y}.$$ La fonction $b$ est bornée mais elle n'admet pas de limite lorsque $y$ tend vers $0$ (c.f. cours). On en déduit que $\dsp\lim_{y\to 0} xb(x,y)$ n'existe pas donc $\dsp\lim_{y\to 0} f(x,y)$ n'existe pas ( bien que $\dsp\lim_{y\to 0} yb(x,y)$ existe!). Donc $\dsp\lim_{x\to 0}\lim_{y\to 0}f(x,y)$ n'existe pas ! De même pour $\dsp \lim_{y\to 0}\lim_{x\to 0}f(x,y)$ puisque $f(x,y)=f(y,x)$. En revanche, on a pour tout $(x,y)\in \R^2$, avec $xy\neq 0$, $$\abs{f(x,y)}\leq \abs{b(x,y)}(\abs{x}+\abs{y})\leq 2\norme{(x,y)}_\infty\tendvers{(x,y)}{(0,0)}\,0 $$ Pour $(x,y)\in \R^2$ tels que $xy=0$, on a $f(x,y)=0$. On en déduit alors $\dsp \lim_{(x,y)\to (0,0)}f(x,y)=0$