Espaces vectoriels normés
Normes
Sur $\R^3$, parmi les applications suivantes, la quelle n'est pas une norme
- $N_1(x,y,z)=\abs{x}+\abs{y}+2\abs{z}$
- $N_2(x,y,z)=\abs{x}+\abs{y}-2\abs{z}$
- $N_3(x,y,z)=\sqrt{x^2+y^2+z^2}$
- $N_4(x,y,z)= \abs{x}+\abs{y}+2\abs{z}+2\sqrt{x^2+y^2+z^2} $
L'application $N_2$ n'est pas une norme, il suffit de calculer $N_2(0,0,1)$.
Soient $E$ un $\K$-e-v et $N_1,\,N_2$ deux normes sur $E$. La quelles des applications suivantes n'est pas une norme sur $E$.
- $N_1+N_2$
- $N_1N_2$
- $\max(N_1,N_2)$
- $2N_1+N_2$
L'application $N_1N_2$ n'est pas une norme, en effet pour $\lambda=2$, on a $$\forall x\in E\setminus\{0\},\,N_1(2x)N_2(2x)=2N_1(x)\times 2N_2(x)=4N_1(x)N_2(x)\neq 2N_1(x)N_2(x).$$
Soient $$\fonct{\psi}{\R_2[X]}{\R}{P}{P(0)^2+P(1)^2},\quad\fonct{\varphi}{\R_2[X]}{\R}{P}{\abs{P(0)}+\abs{P(1)}+\abs{P(2)}}.$$ Montrer que $\psi$ n'est pas une norme. $\varphi$ est-elle une norme?
Soit $P=X(X-1)\in \R_2[X]$, on a $P\neq 0$ et $\psi(P)=P(0)^2+P(1)^2=0$ donc $\psi $ n'est pas une norme. Il est clair que pour tout $P\in \R_2[X]$ et $\lambda\in \R$, $\varphi(P)\geq 0$ et $\varphi (\lambda P)=\abs{\lambda}\varphi (P)$. D'autre part, si $\varphi(P)=0$ alors $P(0)=P(1)=P(2)=0$ ce qui implique que $P$ a trois racines distincts or $\deg (P)\leq 2$ donc $P=0$. Il reste à vérifier l'inégalité triangulaire. Soient $P,Q\in \R_2[X]$, on a: $$\begin{array}{lcl} \varphi (P+Q)&=&\abs{(P+Q)(0)}+\abs{(P+Q)(1)}+\abs{(P+Q)(2)}\\ &=&\abs{P(0)+Q(0)}+\abs{P(1)+Q(1)}+\abs{P(2)+Q(2)}\\ &\leq& \abs{P(0)}+\abs{Q(0)}+\abs{P(1)}+\abs{Q(1)}+\abs{P(2)}+\abs{Q(2)}=\varphi(P)+\varphi(Q). \end{array}$$ On en déduit alors que $\varphi$ définit une norme sur $\R_2[X]$.
Soient $f_1,f_2,f_3\in \CC([0,1],\R)$, on considère l'application $$\fonct{\varphi}{\R^3}{\R}{(x,y,z)}{\norme{xf_1+yf_2+zf_3}_\infty}.$$ Donner CNS sur $f_1,f_2$ et $f_3$ pour que $\varphi$ soit une norme sur $\R^3$.
Il faut et il suffit que la famille $(f_1,f_2,f_3)$ soit libre dans $\CC([0,1],\R)$.
Soit $E$ un $\K$-evn, montrer que: $$\forall (x,y)\in (E\setminus\{0\})^2,\quad \max\left(\norme{x},\norme{y}\right)\norme{\dfrac{x}{\norme{x}}-\dfrac{y}{\norme{y}}}\leq 2\norme{x-y}.$$
Quitte à remplacer $x$ par $y$, on peut supposer que $\norme{x}\geq \norme{y}$. Ainsi, $$\begin{array}{lcl} \max\left(\norme{x},\norme{y}\right)\norme{\dfrac{x}{\norme{x}}-\dfrac{y}{\norme{y}}}&=&\norme{x-\dfrac{\norme{x}}{\norme{y}}y}=\norme{x-y+y-\dfrac{\norme{x}}{\norme{y}}y}\\ &&\\ &\leq& \norme{x-y}+\norme{y-\dfrac{\norme{x}}{\norme{y}}y}= \norme{x-y}+\left(\dfrac{\norme{x}}{\norme{y}}-1\right)\norme{y}\\ &&\\ &\leq& \norme{x-y}+\left(\dfrac{\norme{x}-\norme{y}}{\norme{y}}\right)\norme{y}\leq \norme{x-y}+\norme{x-y} \end{array}$$
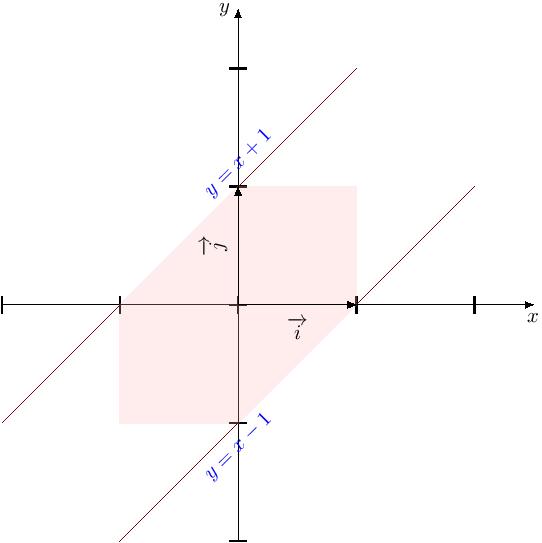
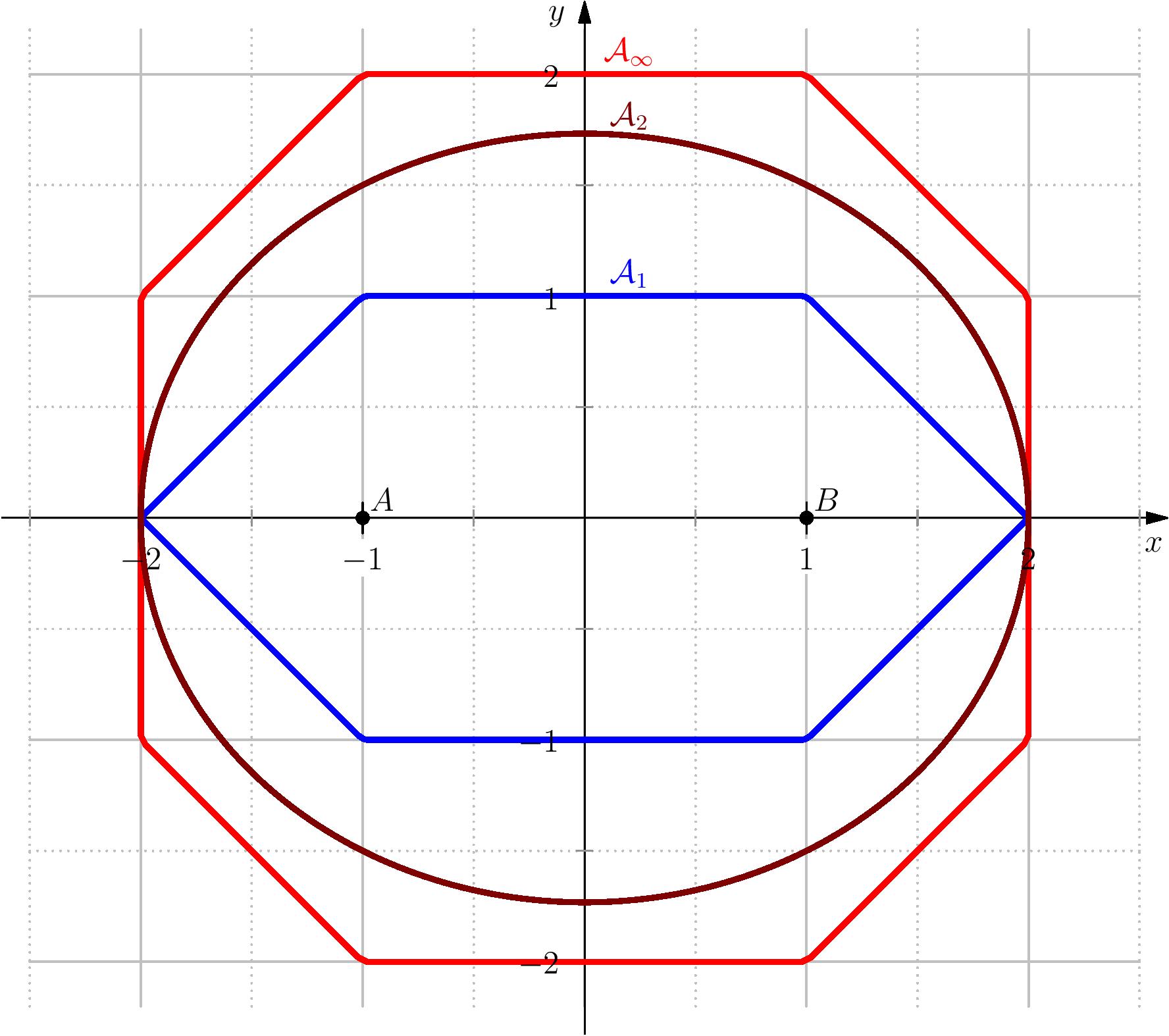
Montrer que $N$, définie sur $\R^2$ par $N(x,y)=\max\left(\abs{x},\abs{y},\abs{x-y}\right)$, est une norme sur $\R^2$ puis représenter la boule unité ouverte.
Il est clair que $N$ définie une norme sur $\R^2$. Pour déterminer la boule unité $B_1$, on remarque que $(x,y)\in B_1$ ssi $\abs{x}< 1$ et $\abs{y}< 1$ et $\abs{x-y}< 1$. Ce qui implique, $x\in ]-1,1[,\,y\in ]-1,1[$ et $x-y\in ]-1,1[$, la dernière relation se traduit par $x-1< y< x+1$.
Soit $(E,\norme{\cdot})$ un $\K$-evn. Montrer: $$\forall x,\,y\in E,\quad \norme{x}+\norme{y}\leq \norme{x+y}+\norme{x-y}.$$
Soient $x,y\in E$, on a $$\norme{2x}=\norme{x+x}=\norme{x+y+x-y}\leq \norme{x+y}+\norme{x-y},$$ $$\norme{2y}=\norme{y+y}=\norme{y+x+y-x}\leq \norme{x+y}+\norme{x-y},$$ en additionnant ces deux relation on obtient la relation demandée.
Soient $n \in \mathbb{N}$ et $E$ l'espace des polynômes réels de degrés inférieurs à $n$. Montrer qu'il existe $\lambda > 0$ vérifiant $$\forall P \in E,\int_0^1 {\left| {P(t)} \right|\,{\mathrm{d}}t} \geqslant \lambda \mathop {\sup }\limits_{t \in \left[ {0,1} \right]} \left| {P(t)} \right|$$
Les application $\fonct{N_1}{E}{\R}{P}{\dsp\int_0^1\abs{P(t)}\ud t}$ et $\fonct{N_2}{E}{\R}{P}{\dsp\mathop {\sup }\limits_{t \in \left[ {0,1} \right]} \left| {P(t)} \right|}$ définissent des normes sur $E$ (je vous laisse la vérification). $E$ étant de dimension finie donc les deux normes sont équivalentes, i.e $$\exists 0< \lambda< \beta\in \R_+,~~\forall P\in E,~~ \lambda N_2(P)\leq N_1(P)\leq \beta N_1(P).$$
Soit $E=\R_1[X]$. On considère les trois normes suivantes: $$N_1(aX+b)=\abs{a}+\abs{b},\quad N_2(aX+b)=\underset{t\in [0,1]}{\max}(\abs{at+b}),\,\text{ et }N_3(aX+b)=\underset{t\in \R}{\max}(\abs{a\ee^{\ii t}+b})$$ Déterminer les plus petits réels $\alpha,\,\beta$ tels que $N_2\leq \alpha N_1\leq \beta N_2$ sur $\R_1[X]$. Faire de même avec $N_1$ et $N_3$.
Comparaison entre $N_1$ et $N_2$.
Soit $P=aX+b\in \R_1[X]$, on a
$$\forall t\in [0,1],\,\abs{at+b}\leq t\abs{a}+\abs{b}\leq \abs{a}+\abs{b} \Longrightarrow N_2(P)\leq N_1(P)$$
On peut alors prendre $\alpha=1$.
D'autre part,
$$\abs{a}=\abs{a+b-b}\leq \abs{a+b}+\abs{b}=\abs{a\times 1+b}+\abs{a\times 0+b}\leq 2N_2(P)$$
et
$\abs{b}=\abs{a \times 0+b}\leq N_2(P)$.
On en déduit alors que $N_1(P)\leq 3N_2(P)$, on peut alors prendre $\beta =3$ (la valeur la plus petite, essayer avec $P=2X-1$).
Comparaison entre $N_1$ et $N_3$.
$$\forall t\in \R,\, \abs{a\ee^{\ii t}+b}\leq \abs{a}\abs{\ee^{\ii t}}+\abs{b}\leq \abs{a}+\abs{b}$$
ce qui donne $N_3\leq N_1$.
D'autre part, pour $t=0 $ si $ab\geq 0$ et $\pi $ sinon, on a
$$\abs{a\ee^{\ii t}+b} =\sqrt{a^2+b^2+2ab\cos(t)} =\sqrt{ (\abs{a}+\abs{b})^2}=N_1(P)$$
donc $N_1\leq N_3$. On en déduit alors que $N_1=N_3$.
- Quelles sont les valeurs de $a \in \R$ pour lesquelles l'application $(x,y) \mapsto N_a (x,y) = \sqrt {x^2 + 2axy + y^2 } $ définit une norme sur $\R^2 $.
- Si $N_a $ et $N_b $ sont des normes, calculer $\mathop {\inf }\limits_{(x,y) \ne 0} \dfrac{{N_a (x,y)}}{{N_b (x,y)}}\text{ et }\mathop {\sup }\limits_{(x,y) \ne 0} \dfrac{{N_a (x,y)}}{{N_b (x,y)}}$
-
On peut écrire $N_a(x,y)=\sqrt{(x+ay)^2+(1-a^2)y^2}$, ainsi pour que $N_a$ soit définie sur $\R^2$ il faut que
$\abs{a}\leq 1$, puis pour que $N_a$ soit une norme il faut que $a\in ]-1,1[$.
supposons maintenant que $a\in ]-1,1[$ et montrons que $N_a$ est une norme.- Il est claire que, pour tout $(x,y)\in \R^2$, $(x+ay)^2+(1-a^2)y^2\geq 0$, donc $N_a\geq 0$.
- Soit $(x,y)\in \R^2$ tel que $N_a(x,y)=0$ alors $(x+ay)^2+(1-a^2)y^2= 0$ soit $x=-ay$ et $y=0$ donc $(x,y)=(0,0)$.
- Soit $(x,y)\in \R^2$ et $\lambda\in \R$, on a $$N_a(\lambda x,\lambda y)=\sqrt{ \lambda^2x^2+2a\lambda^2 xy+\lambda^2y^2} =\abs{\lambda}\sqrt{x^2+2axy+y^2}=\abs{\lambda}N_a(x,y).$$
- Reste à montrer l'inégalité triangulaire. Soient $(x,y),\, (u,v)\in \R^2$, on a $$ \begin{array}{lcl} N_a(x+u,y+v)^2&=& \left( (x+u)^2+2a(x+u)(y+v)+(y+v)^2\right)\\ &=& x^2+2xu+u^2+2a(xy+xv+uy+uv)+y^2+2yv+v^2\\ &=& N_a(x,y)^2 +N_a(u,v)^2 + 2(xu+axv+auy+yv)\quad\quad (\star) \end{array} $$ Puis, $$ \begin{array}{lcl} (xu+axv+auy+yv)^2-N_a(x,y)^2N_a(u,v)^2&=&(xu+axv+auy+yv)^2\\ && - (x^2+2axy+y^2)(u^2+2auv+v^2)\\ &=& -x^2v^2+2xuyv-y^2u^2+a^2 (u^2y^2-2axvuy+x^2v^2)\\ &=&(1-a^2)(xv+uy)^2\leq 0 \end{array} $$ On en déduit alors que $$\abs{xu+axv+auy+yv}\leq N_a(x,y)N_a(u,v)$$ En remplaçant dans la relation $(\star$), on trouve $$N_a(x+u,y+v)^2\leq N_a(x,y)^2+N_a(u,v)^2+2N_a(x,y)N_a(u,v)= \left(N_a(x,y)+N_a(u,v)\right)^2.$$ d'où le résultat (la fonction $x\longmapsto x^2$ est croissante sur $\R_+$).
Remarque On aurait pu montrer que $N_a$ est une norme en utilisant le produit scalire. -
Soient $a,b\in ]-1,1[$, et $(x,y)\in \R^2\setminus \{(0,0)\}$. Si $x=0$ (donc $y\neq 0$) alors $N_a(0,y)=\abs{y}=N_b(0,y)$.
Supposons dans la suite que $x\neq 0$, alors $$\dfrac{N_a(x,y)}{N_b(x,y)}=\sqrt{\dfrac{x^2+2axy+y^2}{x^2+2bxy+y^2}}=\sqrt{\dfrac{1+2a(y/x)+(y/x)^2}{1+2b(y/x)+(y/x)^2}} =\varphi (y/x),$$ avec $\varphi(t)=\sqrt{\dfrac{1+2at+t^2}{1+2bt+t^2}}$, une étude rapide de $\varphi$, donne $$\varphi'(t)=\dfrac{1}{2\varphi(t)}\dfrac{2(b-a)(t^2-1)}{(1+2bt+t^2)^2}\Longrightarrow \varphi'(t)=0 \text{ pour } t=\mp 1.$$ Si $b-a>0$ alors $$\sup_\R \varphi=\varphi (-1) =\sqrt{\dfrac{1-a}{1-b}},\quad \inf_\R\varphi =\varphi(1)=\sqrt{\dfrac{1+a}{1+b}}.$$ Sinon ($b-a < 0$) alors $$\sup_\R \varphi=\varphi (1) =\sqrt{\dfrac{1+a}{1+b}},\quad \inf_\R\varphi =\varphi(-1)=\sqrt{\dfrac{1-a}{1-b}}.$$
Soit $K$ une partie convexe d'un $\R$-e.v $E$, admettant $0_E$ comme centre de symétrie, ne contenant aucune droite vectorielle mais telle que tout droite vectorielle la rencontre en au moins un point distinct de $0_E$.
- Montrer que $N:x\longmapsto \inf\big\{\lambda\in \R_+^*,\, \dfrac{x}{\lambda}\in K\big\}$ est une norme de $E$.
- Montrer que pour cette norme, $B_o(0_E,1)=\overset{\circ}{K}$ et $B_f(0_E,1)=\overline{K}$.
-
Soit $x\in E,\, x\neq 0$, la droite $D=\R x$ rencontre $K$ en un point (au moins) $a\neq 0$, on peut alors écrire
$a=\frac{x}{\alpha}$ avec $\alpha\in \R^*$. Par symétrie, $-a\in K$, mais $-a\in D$, donc
$a,\,-a\in K\cap D$, on en déduit alors que l'ensemble $A_x=\{\lambda\in \R_+^*,\, \frac{x}{\lambda}\in K\}$ est non vide.
(puisque l'un de deux réels $\alpha$ ou $-\alpha$ est strictement positive).
D'autre part, $A_x$ est minoré par $0$, donc $A_x$ admet une borne inférieur.
Ceci prouve déjà que $N(x)$ est bien définie.
Montrons que $N(x)>0$, comme $K$ ne contient pas $D$, alors il existe $y=\beta x\not \in K$ , avec $\beta>0$, ainsi par symétrie $-y=-\beta x\not \in K$. Quitte à changer $\beta$ par $-\beta$, on peut supposer que $\beta>0$, montons que pour tout $\beta'\geq \beta,\, \beta'x\not \in K$.
En effet, soit $\beta'\geq 0$, si on suppose que $\beta' x\in K$, alors par symétrie $-\beta' x\in K$, puis par convexité de $K$, $[-\beta ' x,\beta ' x]\subset K$, ce qui implique que $y=\beta x\in K$ puisque $y\in [-\beta' x,\beta 'x]$, contradiction.
Conclusion, $\forall \beta'\geq \beta,\,\dfrac{1}{\beta'}\not\in A_x$, autrement dit, $N(x)\geq \dfrac{1}{\beta}>0$.
Il est clair que $N(0)=0$, en effet, pour tout $\lambda>0$, $\dfrac{0}{\lambda}=0\in K$, donc $A_0=\R_+^*$ et $\inf (\R_+^*)=0$.
Inversement, si $x\in E$ tel que $N(x)=0$ alors $x=0$, sinon on aurait la droite vectorielle engendré par $x$ inclus dans $K$ ce qui impossible.
Montrons que $N(\beta x)=\abs{\beta}N(x)$.
La relation est évidente pour $x=0$ ou $\beta =0$, supposons alors que $x\neq 0$ et $\beta \neq 0$.
Comme $K$ est symétrique par rapport à $0$, alors on a $$A_{\beta x}=\{\lambda\in \R_+^*,\, \dfrac{\beta x}{\lambda}\in K\} =\{\lambda\in \R_+^*,\, \dfrac{\abs{\beta }x}{\lambda}\in K\}=\{\abs{\beta} \delta, \, \delta >0,\, \dfrac{x}{\delta}\in K\}.$$ Ce qui donne $$N(\beta x)=\inf A_{\beta x}=\abs{\beta}\inf A_x=\abs{\beta}N(x).$$ Il reste à montrer l'inégalité triangulaire.
Soient $x,y\in E$, soient $a\in A_x,\, b\in A_y$, on a $$\dfrac{x}{a}\in \K,\, \dfrac{y}{b}\in K\Longrightarrow \forall t\in [0,1],\quad t \dfrac{x}{a}+(1-t) \dfrac{y}{b}\in K$$ puisque $K$ est convexe. En particulier, si on pose $t = \dfrac{a}{a+b}\in ]0,1[$, on obtient: $$ \dfrac{a}{a+b} \dfrac{x}{a}+\dfrac{b}{a+b} \dfrac{y}{b}= \dfrac{x+y}{a+b}\in K \Longrightarrow a+b\in A_{x+y}, $$ En utilisant la définition de $N$, on obtient $N(x+y)\leq a+b$, ceci étant vrai pour tout $ (a,b)\in A_x\times A_y$, on conclut alors: $N(x+y)\leq N(x)+N(y).$
On fixe maintenant $a\in A_x$, la démarche précédent, nous donne: $$\forall b\in A_y,\quad N(x+y)\leq a+b\Longrightarrow N(x+y)-a\leq N(y)$$ $a$ étant arbitrairement choisi, on a alors, $$\forall a\in A_x,\, N(x+y)-N(y)\leq a \Longrightarrow N(x+y)-N(y)\leq N(x)$$ Ce qui donne la relation demandée.
On trouve finalement que $N$ définie une norme sur $E$. -
Soit $x\in K$, on a $\dfrac{x}{1}\in K$ donc $1\in A_x$ soit $N(x)\leq 1$, autrement dit $K\subset B_f(0,1)$.
Soit $x\in B_o(0,1)$ alors $N(x)< 1$ donc il existe $N(x)\leq a < 1$ tel que $\dfrac{x}{a}\in K$, puis le segment $[0,\dfrac{x}{a}]\subset K$, puisque $a< 1$ alors $x\in [0,\dfrac{x}{a}]$, autrement dit, $x\in K$ soit $B_o(0,1)\subset K$.
On en déduit alors $$B_0(0,1)\subset K\subset B_f(0,1) \Longrightarrow \overline{B_o(0,1)}\subset\overline{K}\subset \overline{B_f(0,1)}$$ Vu que $ \overline{B_o(0,1)}=\overline{B_f(0,1)}=B_f(0,1)$, on déduit alors que $\overline{K}=B_f(0,1)$.
Distance
($\star\star$)
Correction
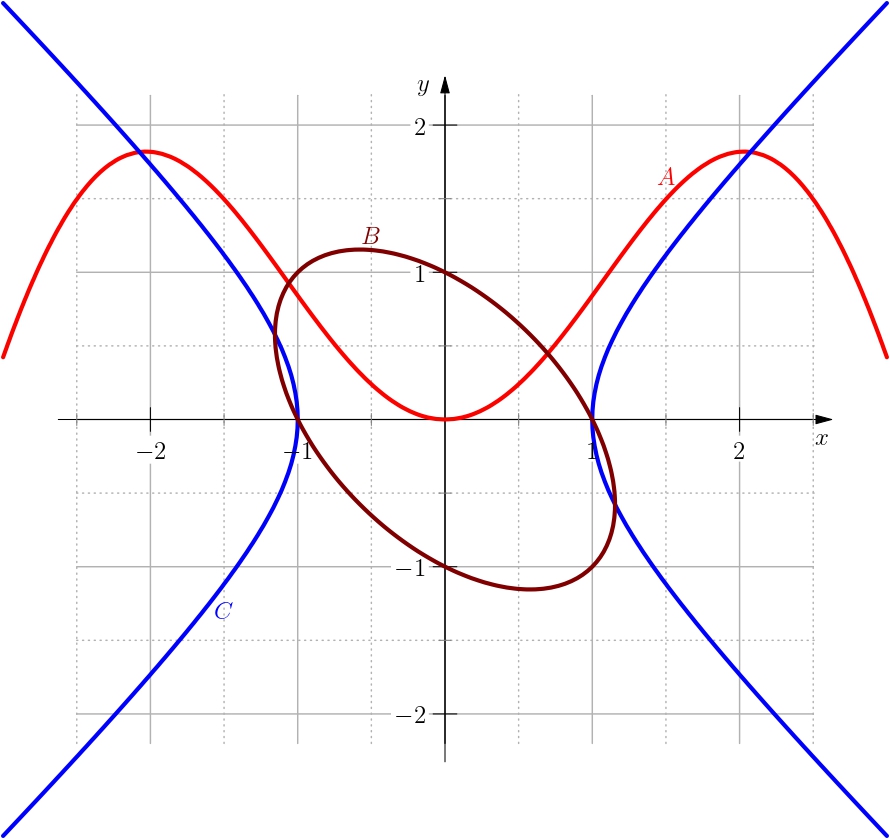
Dans $\R^2$, on considère les points $A=(-1,0)$ et $B=(1,0)$. On note aussi
$\mathcal{A}=\{C=(x,y)\in \R^2,\, N(C-A)+N(C-B)=4\}$ où $N$ désigne la norme sur $\R^2$.
Déterminer et tracer $\mathcal{A}$ dans les cas suivants:
$$ N(x,y)=\norme{(x,y)}_2=\sqrt{x^2+y^2},\quad N(x,y)=\norme{(x,y)}_1=\abs{x}+\abs{y},\quad
N(x,y)=\norme{(x,y)}_\infty= \max (\abs{x},\abs{y}).$$
Correction
On remarque que si $(x,y)\in \mathcal{A}$ alors les points $(-x,y),\, (x,-y),\,(-x,-y)$ sont aussi dans $\mathcal{A}$, puisque
$$ \norme{(x,y)-A}=\norme{(x,-y)-A}=\norme{(-x,y)-B}=\norme{(-x,-y)-B},\, ....$$
( cela marche dans ce cas grâce à la symétrie des points $A$ et $B$ par rapport à l'origine), on peut alors limiter l'étude
sur l'ensembe $\R_+^2$ puis compléter par symétrie.
1ère cas: $N=\norme{\cdot}_2$.
soient $x,y\geq 0$, on a:
$$
\begin{array}{lcl}
(x,y)\in \mathcal{A}_2 &\Longleftrightarrow& (x-1)^2+y^2 = 16 +(x+1)^2+y^2-8\sqrt{(x+1)^2+y^2 }\\
&\Longleftrightarrow& -2x=16+2x -8\sqrt{(x+1)^2+y^2 }\\
&\Longleftrightarrow& (4x+16)^2=64 ((x+1)^2+y^2)\\
&\Longleftrightarrow& 16x^2+128x+256=64x^2+128x+64+64y^2\\
&\Longleftrightarrow& 48x^2+64y^2=192
\end{array}
$$
Donc (en utilsant les symétries) $\mathcal{A}_2=\{(x,y)\in \R^2,\, \dfrac{x^4}{4}+\dfrac{y^2}{3}=1\}$.
2ème cas: $N=\norme{\cdot}_1$.
soient $x,y\geq 0$, on a:
$\quad 2-1$ si $x\leq 1$ alors
$$
\begin{array}{lcl}
\abs{x-1}+\abs{y}+\abs{x+1}+\abs{y}=4&\Longleftrightarrow& 1-x+y+x+1+y=4 \\
&\Longleftrightarrow& 2y+2=4 \Longleftrightarrow y=1.
\end{array}
$$
$\quad 2-2$ si $1\leq x\leq 2$ alors
$$
\begin{array}{lcl}
\abs{x-1}+\abs{y}+\abs{x+1}+\abs{y}=4&\Longleftrightarrow& x-1+y+x+1+y=4 \\
&\Longleftrightarrow& 2y+2x=4 \Longleftrightarrow y=2-x.
\end{array}
$$
$\quad 2-2$ si $2 < x$ alors dans ce cas il n'y a pas de solutions.
3ème cas: $N=\norme{\cdot}_\infty$.
soient $x,y\geq 0$, on a:
$\quad 3-1-a) $ si $x\geq 1$ et $y\leq x-1 $ alors
$$
\begin{array}{lcl}
\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4&\Longleftrightarrow& x-1+x+1=4 \\
&\Longleftrightarrow& x=2.
\end{array}
$$
$\quad 3-1-b)$ si $x\geq 1$ et $ x-1 \leq y \leq x+1$ alors
$$
\begin{array}{lcl}
\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4&\Longleftrightarrow& y+x+1=4 \\
&\Longleftrightarrow& y=3-2x.
\end{array}
$$
$\quad 3-1-c)$ si $x\geq 1$ et $ x+1 < y$ alors dans ce cas il n'y a pas de solutions.
$\quad 3-2-a)$ si $x < 1$ et $y\leq 1-x$, alors
$$\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4 \Longleftrightarrow 1-x+1+x=4\Longleftrightarrow 2=4.$$
Ce qui est impossible, donc il n'y a pas de solutions dans ce cas.
$\quad 3-2-a)$ si $x < 1$ et $1-x \leq y \leq 1+x $, alors
$$\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4 \Longleftrightarrow y +1+x=4\Longleftrightarrow x+y=3 \Longleftrightarrow (x,y)=(1,2).$$
$\quad 3-2-c)$ si $x < 1$ et $ 1+x < y $, alors
$$\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4 \Longleftrightarrow 2y=4 \Longleftrightarrow y=2.$$
En résumé,
($\star\star$)
Correction
Soit $A$ une partie non vide d'un e.v.n $E$.
- Montrer que l'application $x \mapsto \ud (x,A)$ est lipschitzienne de rapport 1.
- Montrer que : $x \in \overline{A} \Longleftrightarrow \ud (x,A) = 0$.
- Montrer que : $ \forall x \in E, \ \ud (x,A) = \ud (x,\overline{A})$.
- Pour $x \in E$, comparer $\ud(x,A)$ à $\ud (x,\overset{\circ}{A})$.
Correction
- L'application $\ud$ est bien définie (c.f. cours). Soient $x,y\in E$, on a
$$\forall z\in A,~\ud(x,A)\leq \norme{x-z}\leq \norme{x-y}+\norme{y-z}$$
ce qui donne:
$$\forall z\in A,~~\ud(x,A)- \norme{x-y}\leq \norme{y-z}\Longrightarrow \ud(x,A)-
\norme{x-y}\leq \ud(y,A)$$
En échangeant les rôles entre $x$ et $y$, on trouve
$$\ud(y,A)- \norme{y-x}\leq \ud(x,A)\Longrightarrow \boxed{\abs{\ud (x,A)-\ud (y,A)}\leq
\norme{x-y}}.$$
Donc l'application $\ud $ est $1$- lipschitzienne.
- Supposons que $\ud (x,A)=0$. Soit $V\in \mathcal{V} (x)$ alors il existe $r>0$ tel que
$B(x,r)\subset V$.
Comme $\ud (x,A)=0< r$ alors il existe $a\in A$ tel que $\ud (x,a)< r$ donc $a\in
B(x,r)$ ce qui
donne $A\cap V\neq \emptyset$.
On a alors
$$\forall V\in \mathcal{V} (x),~~ A\cap V\neq \emptyset \Longrightarrow x\in
\overline{A}.$$
Inversement, supposons que $x\in \overline{A}$. Alors pour tout $\varepsilon >0$, $A\cap
B(x,\varepsilon)\neq \emptyset$, donc il
existe $a\in A$ tel que $\norme{x-a}< \varepsilon$.
Soit $0\leq \ud (x,A)\leq \varepsilon$, en faisant $\varepsilon$ tendre vers $0$ on
trouve $\ud (x,A)=0$.
- Comme $A\subset \overline{A}\,$ on a $\ud (\cdot,\overline{A})\leq \ud (\cdot,A)$.
D'autre part, pour tout $x\in E$ et pour tout $\varepsilon>0$, on a
$$\exists y\in \overline{A},\,\ud (x,y)< \ud
(x,\overline{A})+\dfrac{\varepsilon}{2},\text{ et } \exists a\in A,~~\ud (y,a)<
\dfrac{\varepsilon}{2}.$$
On obtient,
$$\ud (x,a)\leq \ud (x,y)+\ud (y,a)< \ud (x,\overline{A})+\varepsilon\Longrightarrow
\forall \varepsilon>0,\,\ud (x,A)< \ud (x,\overline{A})+\varepsilon$$
donc $\ud (\cdot,\overline{A})\geq \ud (\cdot,A)$; puis $\ud (\cdot,\overline{A})= \ud
(\cdot,A)$.
- On a $\ud (\cdot,A)\leq \ud (\cdot,\overset{\circ}{A})$, on peut avoir une inégalité
strict.
Topologie d'un EVN
($\star$)
Correction
Les ensembles suivants sont-ils bornés?
$$A=\{x\sin(x),\,x\in \R\},\quad B=\{(x,y)\in \R^2,\, x^2+xy+y^2=1\},$$
et $C=\{(x,y)\in \R^2,\,\,x^2-y^2=1\}.$
($\star\star$)
Correction
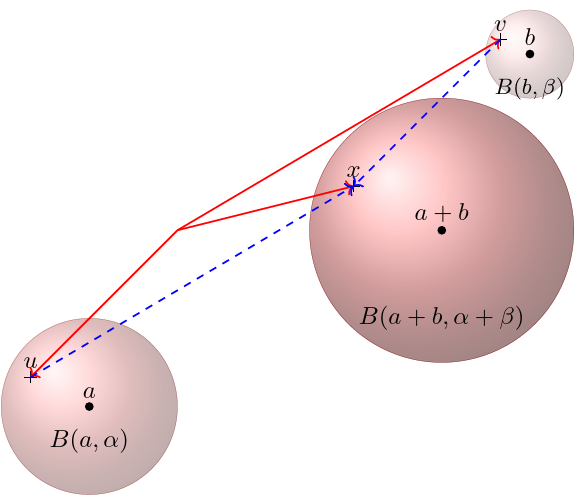
Soient $E$ un $\K$-evn, $a,b\in E$, $\alpha,\beta,\in \R_+^*$ et $\lambda\in \R^*$. Montrer
les relations suivantes:
$$\mathbf{a}) \,\,B(a+b,\alpha+\beta)=B(a,\alpha)+B(b,\beta),\quad \quad \mathbf{b}) \,\,
B(\lambda a, \abs{\lambda} \alpha)=\lambda B(a,\alpha).$$
Correction
Soient $u\in B(a,\alpha),\,v\in B(b,\beta)$, on a
$$\norme{(a+b)-(u+v)}\leq \norme{a-u}+\norme{b-v}< \alpha+\beta.$$
Donc $ u+v\in B(a+b,\alpha+\beta)$, ce qui implique que $B(a,\alpha)+B(b,\beta)\subset
B(a+b,\alpha+\beta)$.
Inversement, soit $x\in B(a+b,\alpha +\beta)$, on pose
$u=\dfrac{\alpha}{\alpha+\beta}(x-(a+b))+a,$ et $v=\dfrac{\beta}{\alpha+\beta}(x-(a+b))+b$.
$$\left\{\begin{array}{lcl}
u+v&=&\dfrac{\alpha}{\alpha+\beta}(x-(a+b))+a+\dfrac{\beta}{\alpha+\beta}(x-(a+b))+b\\
\norme{u-a}&=&\norme{\dfrac{\alpha}{\alpha+\beta}(x-(a+b))}=\dfrac{\alpha}{\alpha+\beta}\norme{x-(a+b)}<
\alpha\Longrightarrow u\in B(a,\alpha),\\
\norme{v-b}&=&\norme{\dfrac{\beta}{\alpha+\beta}(x-(a+b))}=\dfrac{\alpha}{\alpha+\beta}\norme{x-(a+b)}<
\beta\Longrightarrow v\in B(b,\beta),
\end{array}
\right.
$$
On en déduit que $B(a+b,\alpha+\beta)\subset B(a,\alpha)+B(b,\beta)$ ce qui prouve
l'égalité.
($\star$)
Correction
Soit $A$ un ensemble non vide de $E$ convexe. Montrer que $\overset{\circ}{A}$ est un
ensemble convexe.
Correction
Soient $x,y\in \overset{\circ}{A}$ et $\lambda\in ]0,1[$. Alors il existe $\varepsilon_1>0$
(resp. $\varepsilon_2>0$) tel que $B(x,\varepsilon_1)\subset A$ (resp.
$B(y,\varepsilon_2)\subset A$). On note alors $\varepsilon =\min
(\varepsilon_1,\varepsilon_2)$, alors
$$B(\lambda x+(1-\lambda)y,\varepsilon)=B(\lambda
x,\varepsilon)+B((1-\lambda)y,\varepsilon)=\lambda
B(x,\varepsilon)+(1-\lambda)B(y,\varepsilon)\subset A$$
(E3A 2017)
Correction
Soit $F$ un s-e-v de $E$. Montrer que si l'intérieur de $F$ est non vide alors $F=E$.
Correction
Soit $a \in \overset{\circ}{F}$. Il existe donc $r>0$ tel que $B(a,r)\subset F$. Si $x$ est
un vecteur quelconque de $E$,
différent de $a$, alors le vecteur $a+\dfrac{r}{2\norme{x-a}}(x-a)$ appartient à $B(a,r)$
donc à $F$. Par la suite,
$x\in F$ puisque $F$ est un sev, ce qui prouve $F=E$.
($\star$)
Correction
On considère $A=\{\dfrac{1}{x+n}+\dfrac{1}{2^n}; (x,n)\in \R_+^*\times \N^*\}$. Déterminer
$\overset{\circ}{A}$ et $\overline{A}$.
Correction
Pour $n\in \N^*$, on note $A_n=\left\{\dfrac{1}{x+n}+\dfrac{1}{2^n}; x\in \R_+^*\right\}$,
alors $A=\dsp\underset{n\geq 1}{\bigcup}A_n$.
Une étude rapide de la fonction $\fonct{f_n}{\R_+^*}{\R}{x}{\dfrac{1}{x+n}+\dfrac{1}{2^n}}$
montre que $f_n$ est strictement décroissante. Donc
$$A_n=f_n(\R_+^*)=\left]\limiteX{x}{\infty}f_n(x),\limiteX{x}{0^+}f_n(x)\right[=\left]\dfrac{1}{2^n},\dfrac{1}{n}+\dfrac{1}{2^n}\right[$$
Ce qui donne $A=\left]0,\dfrac{3}{2}\right[.$
On en déduit,
$$\boxed{
\overset{\circ}{A}=\left]0,\dfrac{3}{2}\right[,~~~~\overline{A}=\left[0,\dfrac{3}{2}\right]}.$$
($\star$)
Correction
Soient $E$ un e.v.n, $A,B$ deux parties de $E$. On suppose que $A$ et $B$ sont denses dans
$E$ et que $A\cap B=\emptyset$. Montrer que
$\overset{\circ}{A}=\overset{\circ}{B}=\emptyset$.
Correction
Supposons que $\overset{\circ}{A}\neq \emptyset$, soit alors $x\in \overset{\circ}{A}$, il
existe $r>0$ tel que $B(x,r)\subset A$, or comme $B$ est dense dans $E$ alors $B\cap
B(x,r)\neq \emptyset$ donc $B\cap A\neq \emptyset$ contradiction donc
$\boxed{\overset{\circ}{A}=\emptyset}.$
On faite la même démarche pour $B$.
Suites d'un EVN
($\star$)
Correction
Pour $n\in \N$, on pose $u_n=\dfrac{1}{n!}\dsum_{k=0}^nk!$.
-
Montrer que $\dsum_{k=0}^nk!\sim n!$. En déduire que $(u_n)$ converge et donner sa limite.
-
Donner un développement limité à l'ordre 2 de $u_n$ quand $n$ tend vers $\infty$.
Correction
-
Soit $n\in \N,\, n\geq 2$, on a:
$$
\begin{array}{lcl}
n!u_n&=&1+2!+\cdots +n!=n!\left(1+\dfrac{(n-1)!}{n!}+\dfrac{(n-2)!}{n!}+\cdots +\dfrac{2!}{n!}+\dfrac{1}{n!}\right)\\
&=&n!\left(1+\dfrac{1}{n}+\dfrac{1}{n(n-1)}+\cdots +\dfrac{2!}{n!}+\dfrac{1}{n!}\right)
\end{array}
$$
Pour $j\in \inter{1,n-2}$, on a $ \dfrac{j!}{n!}\leq \dfrac{1}{n(n-1)}$ ce qui donne:
$$\forall n\geq 2,\quad n!\leq n!u_n\leq n!\left(1+\dfrac{1}{n}+\dfrac{n-2}{n(n-1)}\right) \Longrightarrow u_n\backsim 1$$
-
Soit $n\geq 4$, on a
$$0\leq \dfrac{1}{n!}\dsum_{k=0}^{n-4}k! \leq \dfrac{(n-3)\times (n-4)!}{n!}=\dfrac{1}{n(n-1)(n-2)}.$$
Ce qui donne,
$$
\begin{array}{lcl}
u_n&=&1+\dfrac{1}{n}+\dfrac{1}{n(n-1)}+\dfrac{1}{n(n-1)(n-2)}+\dfrac{1}{n!}\dsum_{k=0}^{n-4}k!\\
&&\\
&=&1+\dfrac{1}{n}+\dfrac{1}{n(n-1)}+\underset{n\to \infty}{\mathrm{o}}\left(\frac{1}{n^2}\right)\\
&&\\
&=&1+\dfrac{1}{n}+\dfrac{1}{n^2}\left(1+\dfrac{1}{n}+\underset{n\to \infty}{\mathrm{o}}\left(\frac{1}{n}\right)\right)+\underset{n\to \infty}{\mathrm{o}}\left(\frac{1}{n^2}\right)\\
&&\\
&=&1+\dfrac{1}{n}+\dfrac{1}{n^2}+\underset{n\to \infty}{\mathrm{o}}\left(\frac{1}{n^2}\right)
\end{array}
$$
($\star\star$)
Correction
Soient $E$ un $\K$-EVN et $(u_n)$ une suite bornée de $E^\N$. On suppose que la suite $v =(u_n+\frac{u_{2n}}{2})_n$ converge vers 0.
-
Montrer que la suite $u$ converge vers $0$.
-
Le résultat reste vraie si $v$ tend vers une limite $\ell \neq 0$?
Correction
-
Soit $n\in \N^*$, on a
$$v_n=u_n+\dfrac{u_{2n}}{2}\Longrightarrow u_n=v_n-\dfrac{u_{2n}}{2}$$
puis
$$ u_n=v_n-\left(v_{2n}-\dfrac{u_{4n}}{4}\right)=v_n-\dfrac{v_{2n}}{2}+\dfrac{u_{4n}}{4}=v_n-\dfrac{v_{2n}}{2}+\dfrac{v_{4n}}{4}-\dfrac{u_{8n}}{8}.$$
On peut alors montrer par récurrence sur $k\in \N$, que
$$\forall k\in \N,\quad u_n=\dsum_{j=0}^k(-1)^k\dfrac{v_{2^jn}}{2^j}+(-1)^{k+1}\dfrac{u_{2^{k+1}n}}{2^{k+1}}.$$
On en déduit, pour tout $n\in \N,\, k\in \N$,
$$\norme{u_n}=\norme{\dsum_{j=0}^k(-1)^k\dfrac{v_{2^jn}}{2^j}+(-1)^{k+1}\dfrac{u_{2^{k+1}n}}{2^{k+1}} }\leq \dsum_{j=0}^k\dfrac{\norme{v_{2^jn}}}{2^j}+\dfrac{\norme{u_{2^{k+1}n}}}{2^{k+1}}$$
Soit $\varepsilon>0$. La suite $(v_n)$ converge vers $0$, donc il existe $n_0$ tel que, pour tout $n\geq n_0$, $\norme{v_n}\leq \dfrac{\varepsilon}{2}$.
La suite $(u_n)$ est bornée, donc il existe $M>0$ tel que pour tout $n$, $\norme{u_n}\leq M$, puis la suite $(\frac{M}{2^k})_k$ converge vers $0$, en particulier, il existe $k_0$
tel que pour tout $k\geq k_0$, $\dfrac{M}{2^{k+1}}\leq \dfrac{\varepsilon}{2}$.
En utilisant les relations précédente, on trouve pour $n\geq n_0,\, k\geq k_0$,
$$\norme{u_n}\leq \dsum_{j=0}^k\dfrac{\norme{v_{2^jn}}}{2^j}+\dfrac{\norme{u_{2^{k+1}n}}}{2^{k+1}}\leq \dfrac{\varepsilon}{2} \dsum_{j=0}^k\dfrac{1}{2^j}+\dfrac{M}{2^{k+1}}\leq \dfrac{\varepsilon}{2} +\dfrac{\varepsilon}{2} =\varepsilon.$$
Ce qui implique que $u_n\tendversN\,0$.
-
Supposons que $v_n\tendversN\,\ell$ alors $w_n=v_n-\ell \tendversN\,0$.
Soit $n\geq 0$, on écrit,
$$w_n=v_n-\ell=u_n+\dfrac{u_{2n}}{2}-(\dfrac{2\ell}{3}+\dfrac{2\ell}{2\times 3})=(u_n-\dfrac{2\ell}{3})+\dfrac{u_{2n}-\dfrac{2\ell}{3}}{2},$$
comme la suite $(u_n)$ est bornée, il en va de même pour la suite
$(u_n-\dfrac{2\ell}{3})$.
On utilise alors le résultat de la question précédente, ce qui donne,
$$u_n-\dfrac{2\ell}{3}\tendversN\,0\Longrightarrow u_n\tendversN\,\dfrac{2\ell}{3}.$$
($\star$)
Correction
On considère les matrices suivantes: $A=\begin{pmatrix}
1/2&0&0\\
0&3/5&0\\0&0&1/3
\end{pmatrix},\,\,B=\begin{pmatrix}
1&0&0\\0&-1&1\\0&0&1
\end{pmatrix}$.
-
Montrer que la suite $\left(A^n\right)_{n\in \N}$ converge dans $\MM_3(\R)$ et déterminer sa limite.
-
Montrer que la suite $\left(B^n\right)_{n\in \N}$ diverge.
Correction
-
La matrice $A$ est une matrice diagonale, donc d'après le cours,
$$A^n=\begin{pmatrix}
(1/2)^n&0&0\\
0&(3/5)^n&0\\
0&0&(1/3)^n
\end{pmatrix}\tendversN\, \begin{pmatrix}
0&0&0\\
0&0&0\\
0&0&0
\end{pmatrix}.$$
-
Commençons par calculer $B^2$,
$$B^2= \begin{pmatrix}
1&0&0\\0&-1&1\\0&0&1
\end{pmatrix}\begin{pmatrix}
1&0&0\\0&-1&1\\0&0&1
\end{pmatrix}
=\begin{pmatrix}
1&0&0\\0&1&0\\0&0&1
\end{pmatrix}=I_3.$$
On en déduit que
$$\forall n\in \N,\quad B^{2n+1}=B,\quad B^{2n}=I_3$$
Comme $B\neq I_3$, alors $(B^n)$ ne converge pas dans $\MM_3(\R)$.
($\star$)
Correction
On considère la matrice $A=\begin{pmatrix}
1&0&0\\
-2&3&1\\
4&-4&-1
\end{pmatrix}$.
-
Calculer $(A-I_3)^2$, en déduire $A^n$, pour $n\in \N$.
-
Montrer que la suite $\left(\frac{1}{n} A^n\right)_{n\in \N^*}$ converge et déterminer sa limite.
Correction
-
Un calcul de $(A-I_3)^2$ donne
$$(A-I_3)^2=0\Longrightarrow A^2=2A-I_3\text{ puis } A^3=A (2A-I_3) =2A^2-A=3A-2I_3 ....$$
donc par récurrence sur $n\in \N^*$, on montre
$$\forall n\in \N^*,\quad A^n=nA-(n-1)I_n.$$
-
D'après la question précédente, on a
$$\forall n\geq 1,\quad \dfrac{1}{n}A^n=A-\dfrac{n-1}{n}I_3\tendversN\, A-I_3.$$
($\star$)
Correction
Soient $A,\,B\in \MM_p(\R)$. On suppose que $(AB)^n\tendversN\,0_p$. Montrer que $(BA)^n\tendversN\,0_p$.
Correction
Il suffit d'écrire,
$$\forall n\geq 2,\quad (BA)^n = (BA) (BA)\cdots (BA)(BA) =B(AB)(AB)\cdots (AB)B=A (AB)^{n-1} B$$
Comme $(AB)^n\tendversN\,0_p$ alors $(AB)^{n-1}\tendversN\,0_p$ ce qui donne le résultat.
($\star$)
Correction
Soit~$B\in\MM_n(\R)$ une matrice antisymétrique, telle que la suite~$\bigl(B^n\bigr)_{n\in\N}$ converge vers une matrice~$C$.
Que peut-on dire de~$C$ ?
Correction
Pour tout $n\in \N$, on a $\left( \,^tB\right)^n=\,^t (B^n)\tendversN \,^t C$. Comme $B$ est antisymétrique alors $\,^tB=-B$ donc
$\left( \,^tB\right)^n=(-B)^n$ donc
$$\left( \,^tB\right)^{2n}=B^{2n}\tendversN\,C,\text{ et } \left( \,^tB\right)^{2n+1}=-B^{2n+1}\tendversN\,-C.$$
Donc $C=-C$ d'où $C=0$.
($\star$)
Correction
Soit $M\in \MM_n(\K)$, on suppose que la suite $(M^n)$ converge vers $A\in \MM_n(\K)$.
-
Montrer que la suite $\left((M^2)^n\right)_n$ converge dans $\MM_n(\K)$.
-
Montrer que $A^2=A$.
Correction
La suite $(M^n)_n$ converge donc toute suite extraite de cette suite converge aussi (vers la
même limite),
en particulier, la suite $(M^{2n})_n$ converge aussi vers $A$ .
Pour tout $n\in \N$, on a $M^{2n}=M^n\times M^n$ ainsi par passage à la limite on trouve $A=
A\times A$.
($\star\star$)
Correction
Soit $E$ un $\K$-evn de dimension finie $p$, et $(x_n)$ une suite d'éléments de $E$. On
suppose que $\dsum \norme{x_n}$ converge dans $\R$, montrer que $\dsum x_n$ converge dans
$E$.
Correction
Soit $\BB=(e_1,\cdots,e_p)$ une base de $E$, pour tout $n\in \N$, on a
$x_n=x_{1,n}e_1+x_{2,n}+\cdots+x_{p,n}e_p$
($(x_{i,n})_n$ est la $i$\up{ème} suite cordonnée de $(x_n)$ relativement à la base
$\BB$).
$E$ étant de dimension finie, donc tout les normes sur $E$ sont équivalentes, on travaille
donc avec la norme
infinie définie par $\norme{\dsum_{k=1}^p a_ke_k}=\max\{\abs{a_k},\,k\in\inter{1,p}\}$.
On a pour tout $i\in \inter{1,p}$ et $n\in \N$, $\abs{x_{i,n}}\leq \norme{x_n}_\infty$, or
$\dsum \norme{x_n}_\infty$ converge. On en déduit alors que $\dsum x_{i,n}$ est absolument
convergente donc convergente. Notons $\ell_i$ sa somme.
$$\forall n\in \N,\quad \dsum_{k=0}^nx_k=\dsum_{k=0}^n (\dsum_{i=1}^p
x_{i,k}e_i)=\dsum_{i=1}^p\left(\dsum_{k=0}^nx_{i,k}\right)e_i\tendversN\,\dsum_{i=1}^p\ell_i
e_i.$$
($\star$)
Correction
Soit $A\subset E$ un ensemble non vide. On suppose que $A$ est convexe. Montrer que
$\overline{A}$ est convexe.
Correction
Soient $x,y\in \overline{A}$ et $\lambda\in ]0,1[$, d'après la proposition précédente, ils
existe deux suites $(x_n),\, (y_n)$ d'éléments de $A$ tels que $x_n\tendversN\,x$ et
$y_n\tendversN \,y$. On considère alors la suite $(w_n)$ définie par $w_n=\lambda
x_n+(1-\lambda)y_n$.
Alors la suite $(w_n)$ vérifie:
$$\forall n\in \N,\,w_n\in A \text{ (car $A$ est convexe) et }w_n\tendversN\,\lambda
x+(1-\lambda)y.$$
Puisque $(w_n)\in A^\N$ alors $\lim w_n\in \overline{A}$, ceci prouve que $\lambda
x+(1-\lambda)y\in \overline{A}$.
($\star$)
Correction
Soit $E=\CC([0,1],\R)$ muni de la norme $\norme{\cdot}_\infty$. On note
$$A=\{f\in E,\, f(0)=0 \text{ et }\dsp\int_0^1f(t)\ud t\geq 1\}.$$
Montrer que $A$ est une partie fermée de $E$.
Correction
Soit $(f_n)$ une suite d'éléments de $A$ qui converge dans $E$ vers $f$, i.e.
$\norme{f_n-f}_\infty\tendversN\,0$.
-
Pour tout $n\in \N$, on a
$$\abs{f_n(0)-f(0)}\leq \norme{f_n-f}_\infty\Longrightarrow\abs{f(0)}\leq
\norme{f_n-f}_\infty\tendversN 0$$
Donc $f(0)=0$.
-
En utilisant les propriétés de l'intégrale,
$$\abs{\int_0^1(f-f_n)}\leq \int_0^1\norme{f-f_n}_\infty\leq
\norme{f-f_n}_\infty\Longrightarrow \int_0^1f_n(t)\ud t\tendversN\,\int_0^1f(t)\ud
t$$
or pour tout $n\in \N,\,\dsp\int_0^1 f_n\geq 1$ donc $\dsp\int_0^1 f(t)\ud t\geq 1$
On en déduit alors que $f\in A$, ce qui prouve que $A$ est un fermé de $E$.
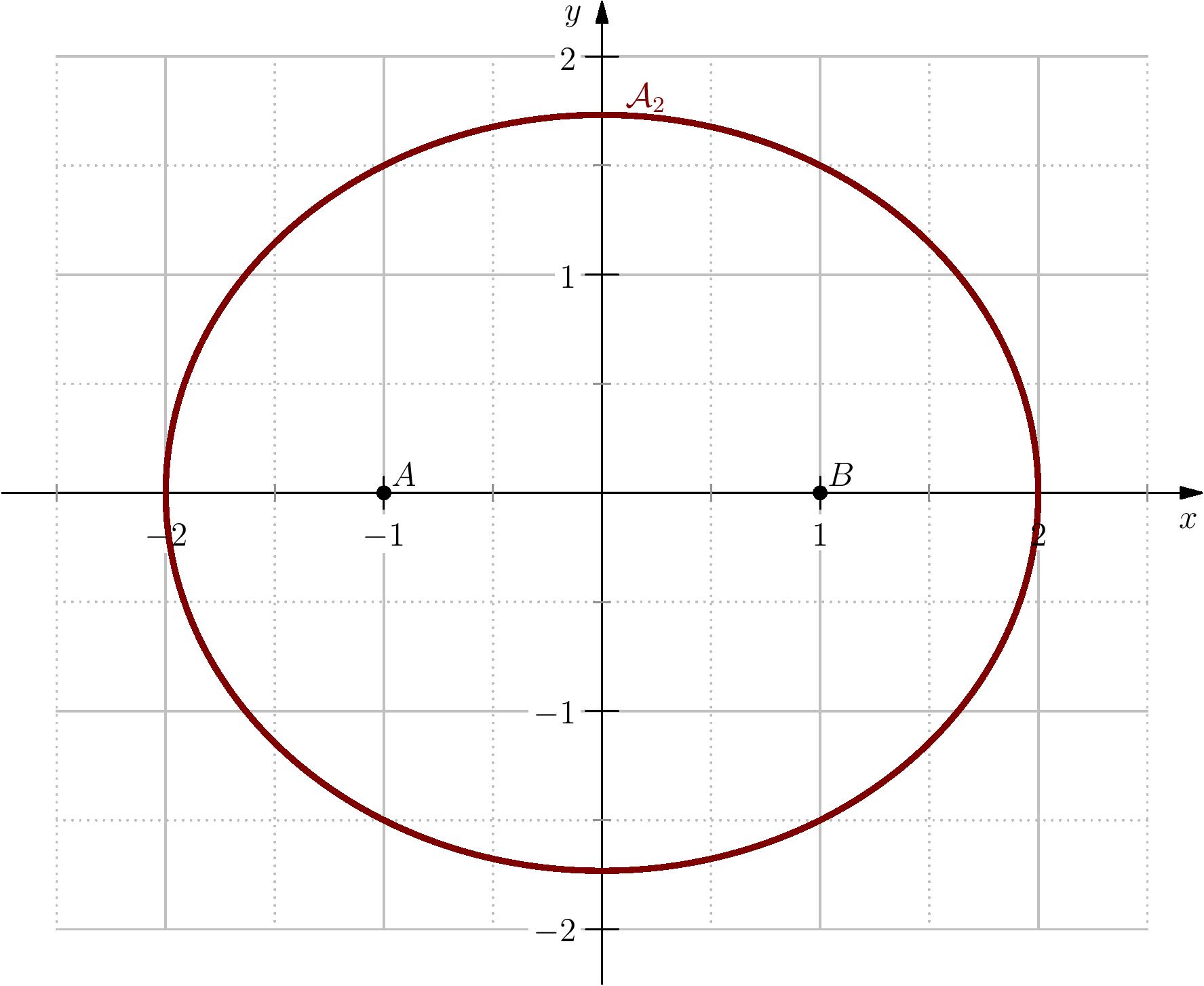
Dans $\R^2$, on considère les points $A=(-1,0)$ et $B=(1,0)$. On note aussi $\mathcal{A}=\{C=(x,y)\in \R^2,\, N(C-A)+N(C-B)=4\}$ où $N$ désigne la norme sur $\R^2$.
Déterminer et tracer $\mathcal{A}$ dans les cas suivants: $$ N(x,y)=\norme{(x,y)}_2=\sqrt{x^2+y^2},\quad N(x,y)=\norme{(x,y)}_1=\abs{x}+\abs{y},\quad N(x,y)=\norme{(x,y)}_\infty= \max (\abs{x},\abs{y}).$$
On remarque que si $(x,y)\in \mathcal{A}$ alors les points $(-x,y),\, (x,-y),\,(-x,-y)$ sont aussi dans $\mathcal{A}$, puisque $$ \norme{(x,y)-A}=\norme{(x,-y)-A}=\norme{(-x,y)-B}=\norme{(-x,-y)-B},\, ....$$ ( cela marche dans ce cas grâce à la symétrie des points $A$ et $B$ par rapport à l'origine), on peut alors limiter l'étude sur l'ensembe $\R_+^2$ puis compléter par symétrie.
1ère cas: $N=\norme{\cdot}_2$.
soient $x,y\geq 0$, on a: $$ \begin{array}{lcl} (x,y)\in \mathcal{A}_2 &\Longleftrightarrow& (x-1)^2+y^2 = 16 +(x+1)^2+y^2-8\sqrt{(x+1)^2+y^2 }\\ &\Longleftrightarrow& -2x=16+2x -8\sqrt{(x+1)^2+y^2 }\\ &\Longleftrightarrow& (4x+16)^2=64 ((x+1)^2+y^2)\\ &\Longleftrightarrow& 16x^2+128x+256=64x^2+128x+64+64y^2\\ &\Longleftrightarrow& 48x^2+64y^2=192 \end{array} $$ Donc (en utilsant les symétries) $\mathcal{A}_2=\{(x,y)\in \R^2,\, \dfrac{x^4}{4}+\dfrac{y^2}{3}=1\}$.
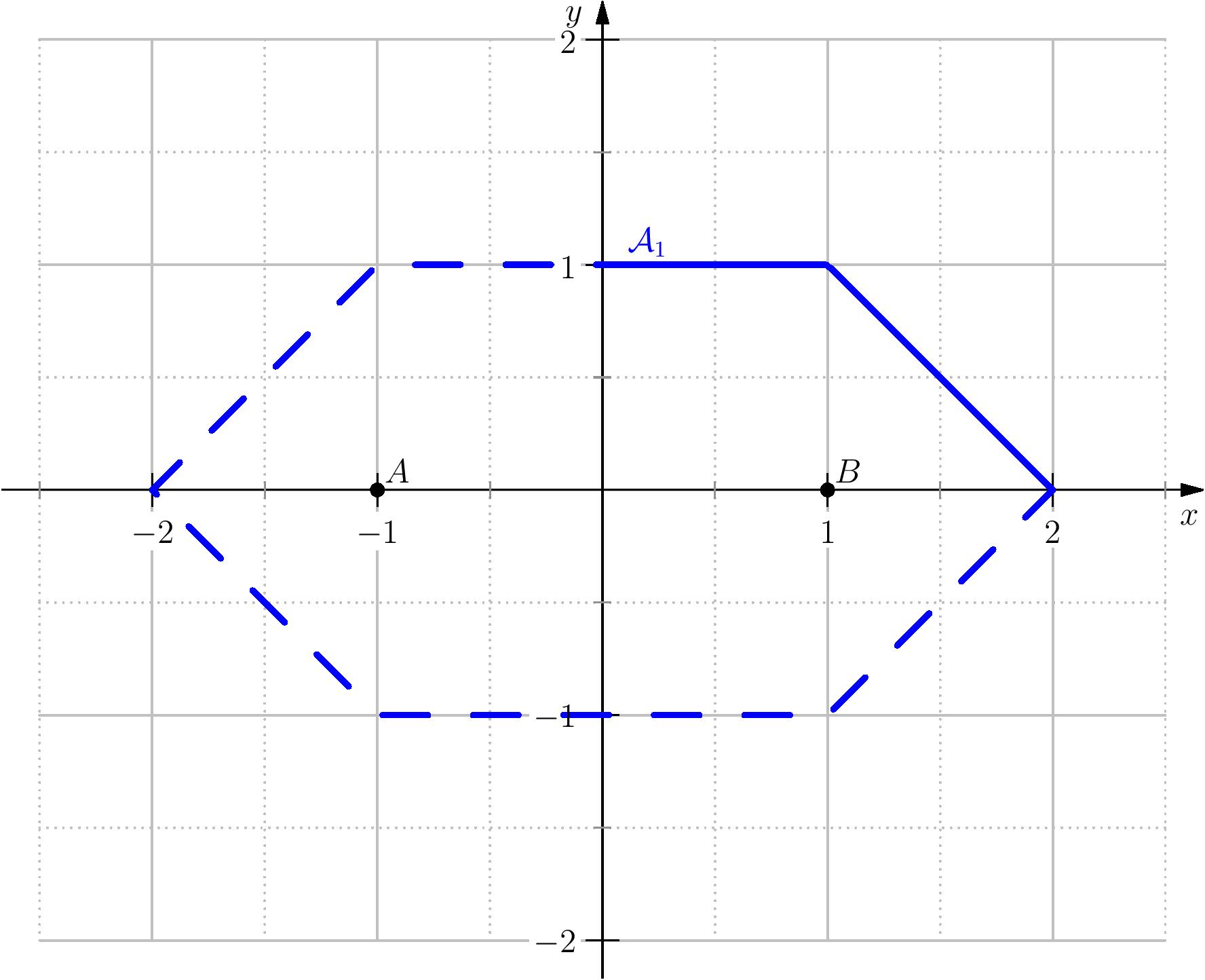
2ème cas: $N=\norme{\cdot}_1$.
soient $x,y\geq 0$, on a:
$\quad 2-1$ si $x\leq 1$ alors
$$
\begin{array}{lcl}
\abs{x-1}+\abs{y}+\abs{x+1}+\abs{y}=4&\Longleftrightarrow& 1-x+y+x+1+y=4 \\
&\Longleftrightarrow& 2y+2=4 \Longleftrightarrow y=1.
\end{array}
$$
$\quad 2-2$ si $1\leq x\leq 2$ alors
$$
\begin{array}{lcl}
\abs{x-1}+\abs{y}+\abs{x+1}+\abs{y}=4&\Longleftrightarrow& x-1+y+x+1+y=4 \\
&\Longleftrightarrow& 2y+2x=4 \Longleftrightarrow y=2-x.
\end{array}
$$
$\quad 2-2$ si $2 < x$ alors dans ce cas il n'y a pas de solutions.
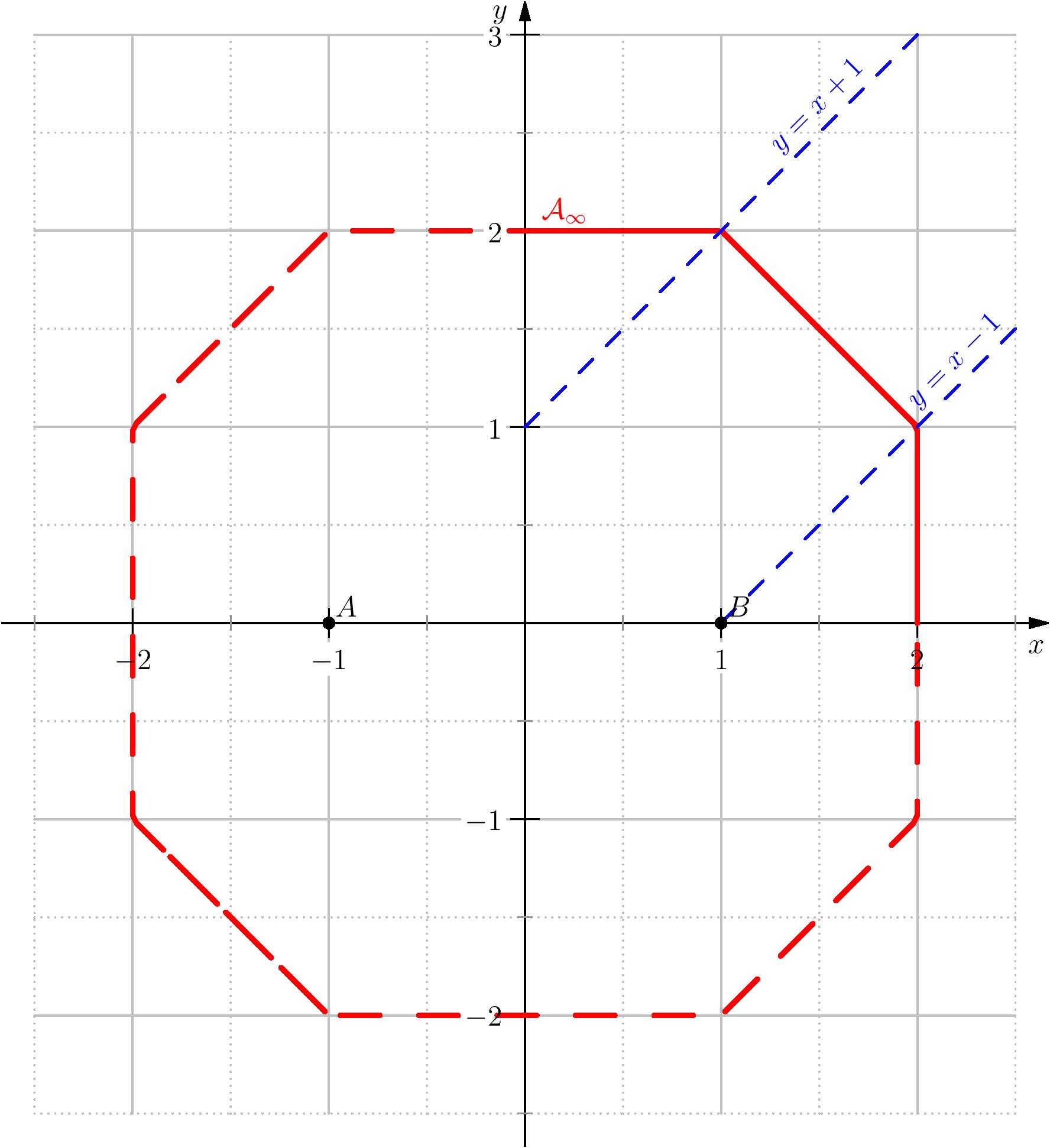
3ème cas: $N=\norme{\cdot}_\infty$.
soient $x,y\geq 0$, on a:
$\quad 3-1-a) $ si $x\geq 1$ et $y\leq x-1 $ alors
$$
\begin{array}{lcl}
\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4&\Longleftrightarrow& x-1+x+1=4 \\
&\Longleftrightarrow& x=2.
\end{array}
$$
$\quad 3-1-b)$ si $x\geq 1$ et $ x-1 \leq y \leq x+1$ alors
$$
\begin{array}{lcl}
\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4&\Longleftrightarrow& y+x+1=4 \\
&\Longleftrightarrow& y=3-2x.
\end{array}
$$
$\quad 3-1-c)$ si $x\geq 1$ et $ x+1 < y$ alors dans ce cas il n'y a pas de solutions.
$\quad 3-2-a)$ si $x < 1$ et $y\leq 1-x$, alors
$$\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4 \Longleftrightarrow 1-x+1+x=4\Longleftrightarrow 2=4.$$
Ce qui est impossible, donc il n'y a pas de solutions dans ce cas.
$\quad 3-2-a)$ si $x < 1$ et $1-x \leq y \leq 1+x $, alors
$$\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4 \Longleftrightarrow y +1+x=4\Longleftrightarrow x+y=3 \Longleftrightarrow (x,y)=(1,2).$$
$\quad 3-2-c)$ si $x < 1$ et $ 1+x < y $, alors
$$\max(\abs{x-1},\abs{y})+\max(\abs{x+1},\abs{y})=4 \Longleftrightarrow 2y=4 \Longleftrightarrow y=2.$$
En résumé,
Soit $A$ une partie non vide d'un e.v.n $E$.
- Montrer que l'application $x \mapsto \ud (x,A)$ est lipschitzienne de rapport 1.
- Montrer que : $x \in \overline{A} \Longleftrightarrow \ud (x,A) = 0$.
- Montrer que : $ \forall x \in E, \ \ud (x,A) = \ud (x,\overline{A})$.
- Pour $x \in E$, comparer $\ud(x,A)$ à $\ud (x,\overset{\circ}{A})$.
- L'application $\ud$ est bien définie (c.f. cours). Soient $x,y\in E$, on a $$\forall z\in A,~\ud(x,A)\leq \norme{x-z}\leq \norme{x-y}+\norme{y-z}$$ ce qui donne: $$\forall z\in A,~~\ud(x,A)- \norme{x-y}\leq \norme{y-z}\Longrightarrow \ud(x,A)- \norme{x-y}\leq \ud(y,A)$$ En échangeant les rôles entre $x$ et $y$, on trouve $$\ud(y,A)- \norme{y-x}\leq \ud(x,A)\Longrightarrow \boxed{\abs{\ud (x,A)-\ud (y,A)}\leq \norme{x-y}}.$$ Donc l'application $\ud $ est $1$- lipschitzienne.
- Supposons que $\ud (x,A)=0$. Soit $V\in \mathcal{V} (x)$ alors il existe $r>0$ tel que $B(x,r)\subset V$. Comme $\ud (x,A)=0< r$ alors il existe $a\in A$ tel que $\ud (x,a)< r$ donc $a\in B(x,r)$ ce qui donne $A\cap V\neq \emptyset$. On a alors $$\forall V\in \mathcal{V} (x),~~ A\cap V\neq \emptyset \Longrightarrow x\in \overline{A}.$$ Inversement, supposons que $x\in \overline{A}$. Alors pour tout $\varepsilon >0$, $A\cap B(x,\varepsilon)\neq \emptyset$, donc il existe $a\in A$ tel que $\norme{x-a}< \varepsilon$. Soit $0\leq \ud (x,A)\leq \varepsilon$, en faisant $\varepsilon$ tendre vers $0$ on trouve $\ud (x,A)=0$.
- Comme $A\subset \overline{A}\,$ on a $\ud (\cdot,\overline{A})\leq \ud (\cdot,A)$.
D'autre part, pour tout $x\in E$ et pour tout $\varepsilon>0$, on a $$\exists y\in \overline{A},\,\ud (x,y)< \ud (x,\overline{A})+\dfrac{\varepsilon}{2},\text{ et } \exists a\in A,~~\ud (y,a)< \dfrac{\varepsilon}{2}.$$ On obtient, $$\ud (x,a)\leq \ud (x,y)+\ud (y,a)< \ud (x,\overline{A})+\varepsilon\Longrightarrow \forall \varepsilon>0,\,\ud (x,A)< \ud (x,\overline{A})+\varepsilon$$ donc $\ud (\cdot,\overline{A})\geq \ud (\cdot,A)$; puis $\ud (\cdot,\overline{A})= \ud (\cdot,A)$. - On a $\ud (\cdot,A)\leq \ud (\cdot,\overset{\circ}{A})$, on peut avoir une inégalité strict.
Les ensembles suivants sont-ils bornés? $$A=\{x\sin(x),\,x\in \R\},\quad B=\{(x,y)\in \R^2,\, x^2+xy+y^2=1\},$$ et $C=\{(x,y)\in \R^2,\,\,x^2-y^2=1\}.$
Soient $E$ un $\K$-evn, $a,b\in E$, $\alpha,\beta,\in \R_+^*$ et $\lambda\in \R^*$. Montrer les relations suivantes: $$\mathbf{a}) \,\,B(a+b,\alpha+\beta)=B(a,\alpha)+B(b,\beta),\quad \quad \mathbf{b}) \,\, B(\lambda a, \abs{\lambda} \alpha)=\lambda B(a,\alpha).$$
Soient $u\in B(a,\alpha),\,v\in B(b,\beta)$, on a $$\norme{(a+b)-(u+v)}\leq \norme{a-u}+\norme{b-v}< \alpha+\beta.$$ Donc $ u+v\in B(a+b,\alpha+\beta)$, ce qui implique que $B(a,\alpha)+B(b,\beta)\subset B(a+b,\alpha+\beta)$. Inversement, soit $x\in B(a+b,\alpha +\beta)$, on pose $u=\dfrac{\alpha}{\alpha+\beta}(x-(a+b))+a,$ et $v=\dfrac{\beta}{\alpha+\beta}(x-(a+b))+b$. $$\left\{\begin{array}{lcl} u+v&=&\dfrac{\alpha}{\alpha+\beta}(x-(a+b))+a+\dfrac{\beta}{\alpha+\beta}(x-(a+b))+b\\ \norme{u-a}&=&\norme{\dfrac{\alpha}{\alpha+\beta}(x-(a+b))}=\dfrac{\alpha}{\alpha+\beta}\norme{x-(a+b)}< \alpha\Longrightarrow u\in B(a,\alpha),\\ \norme{v-b}&=&\norme{\dfrac{\beta}{\alpha+\beta}(x-(a+b))}=\dfrac{\alpha}{\alpha+\beta}\norme{x-(a+b)}< \beta\Longrightarrow v\in B(b,\beta), \end{array} \right. $$ On en déduit que $B(a+b,\alpha+\beta)\subset B(a,\alpha)+B(b,\beta)$ ce qui prouve l'égalité.
Soit $A$ un ensemble non vide de $E$ convexe. Montrer que $\overset{\circ}{A}$ est un ensemble convexe.
Soient $x,y\in \overset{\circ}{A}$ et $\lambda\in ]0,1[$. Alors il existe $\varepsilon_1>0$ (resp. $\varepsilon_2>0$) tel que $B(x,\varepsilon_1)\subset A$ (resp. $B(y,\varepsilon_2)\subset A$). On note alors $\varepsilon =\min (\varepsilon_1,\varepsilon_2)$, alors $$B(\lambda x+(1-\lambda)y,\varepsilon)=B(\lambda x,\varepsilon)+B((1-\lambda)y,\varepsilon)=\lambda B(x,\varepsilon)+(1-\lambda)B(y,\varepsilon)\subset A$$
Soit $F$ un s-e-v de $E$. Montrer que si l'intérieur de $F$ est non vide alors $F=E$.
Soit $a \in \overset{\circ}{F}$. Il existe donc $r>0$ tel que $B(a,r)\subset F$. Si $x$ est un vecteur quelconque de $E$, différent de $a$, alors le vecteur $a+\dfrac{r}{2\norme{x-a}}(x-a)$ appartient à $B(a,r)$ donc à $F$. Par la suite, $x\in F$ puisque $F$ est un sev, ce qui prouve $F=E$.
On considère $A=\{\dfrac{1}{x+n}+\dfrac{1}{2^n}; (x,n)\in \R_+^*\times \N^*\}$. Déterminer $\overset{\circ}{A}$ et $\overline{A}$.
Pour $n\in \N^*$, on note $A_n=\left\{\dfrac{1}{x+n}+\dfrac{1}{2^n}; x\in \R_+^*\right\}$, alors $A=\dsp\underset{n\geq 1}{\bigcup}A_n$. Une étude rapide de la fonction $\fonct{f_n}{\R_+^*}{\R}{x}{\dfrac{1}{x+n}+\dfrac{1}{2^n}}$ montre que $f_n$ est strictement décroissante. Donc $$A_n=f_n(\R_+^*)=\left]\limiteX{x}{\infty}f_n(x),\limiteX{x}{0^+}f_n(x)\right[=\left]\dfrac{1}{2^n},\dfrac{1}{n}+\dfrac{1}{2^n}\right[$$ Ce qui donne $A=\left]0,\dfrac{3}{2}\right[.$ On en déduit, $$\boxed{ \overset{\circ}{A}=\left]0,\dfrac{3}{2}\right[,~~~~\overline{A}=\left[0,\dfrac{3}{2}\right]}.$$
Soient $E$ un e.v.n, $A,B$ deux parties de $E$. On suppose que $A$ et $B$ sont denses dans $E$ et que $A\cap B=\emptyset$. Montrer que $\overset{\circ}{A}=\overset{\circ}{B}=\emptyset$.
Supposons que $\overset{\circ}{A}\neq \emptyset$, soit alors $x\in \overset{\circ}{A}$, il existe $r>0$ tel que $B(x,r)\subset A$, or comme $B$ est dense dans $E$ alors $B\cap B(x,r)\neq \emptyset$ donc $B\cap A\neq \emptyset$ contradiction donc $\boxed{\overset{\circ}{A}=\emptyset}.$ On faite la même démarche pour $B$.
Pour $n\in \N$, on pose $u_n=\dfrac{1}{n!}\dsum_{k=0}^nk!$.
- Montrer que $\dsum_{k=0}^nk!\sim n!$. En déduire que $(u_n)$ converge et donner sa limite.
- Donner un développement limité à l'ordre 2 de $u_n$ quand $n$ tend vers $\infty$.
- Soit $n\in \N,\, n\geq 2$, on a: $$ \begin{array}{lcl} n!u_n&=&1+2!+\cdots +n!=n!\left(1+\dfrac{(n-1)!}{n!}+\dfrac{(n-2)!}{n!}+\cdots +\dfrac{2!}{n!}+\dfrac{1}{n!}\right)\\ &=&n!\left(1+\dfrac{1}{n}+\dfrac{1}{n(n-1)}+\cdots +\dfrac{2!}{n!}+\dfrac{1}{n!}\right) \end{array} $$ Pour $j\in \inter{1,n-2}$, on a $ \dfrac{j!}{n!}\leq \dfrac{1}{n(n-1)}$ ce qui donne: $$\forall n\geq 2,\quad n!\leq n!u_n\leq n!\left(1+\dfrac{1}{n}+\dfrac{n-2}{n(n-1)}\right) \Longrightarrow u_n\backsim 1$$
- Soit $n\geq 4$, on a $$0\leq \dfrac{1}{n!}\dsum_{k=0}^{n-4}k! \leq \dfrac{(n-3)\times (n-4)!}{n!}=\dfrac{1}{n(n-1)(n-2)}.$$ Ce qui donne, $$ \begin{array}{lcl} u_n&=&1+\dfrac{1}{n}+\dfrac{1}{n(n-1)}+\dfrac{1}{n(n-1)(n-2)}+\dfrac{1}{n!}\dsum_{k=0}^{n-4}k!\\ &&\\ &=&1+\dfrac{1}{n}+\dfrac{1}{n(n-1)}+\underset{n\to \infty}{\mathrm{o}}\left(\frac{1}{n^2}\right)\\ &&\\ &=&1+\dfrac{1}{n}+\dfrac{1}{n^2}\left(1+\dfrac{1}{n}+\underset{n\to \infty}{\mathrm{o}}\left(\frac{1}{n}\right)\right)+\underset{n\to \infty}{\mathrm{o}}\left(\frac{1}{n^2}\right)\\ &&\\ &=&1+\dfrac{1}{n}+\dfrac{1}{n^2}+\underset{n\to \infty}{\mathrm{o}}\left(\frac{1}{n^2}\right) \end{array} $$
Soient $E$ un $\K$-EVN et $(u_n)$ une suite bornée de $E^\N$. On suppose que la suite $v =(u_n+\frac{u_{2n}}{2})_n$ converge vers 0.
- Montrer que la suite $u$ converge vers $0$.
- Le résultat reste vraie si $v$ tend vers une limite $\ell \neq 0$?
-
Soit $n\in \N^*$, on a
$$v_n=u_n+\dfrac{u_{2n}}{2}\Longrightarrow u_n=v_n-\dfrac{u_{2n}}{2}$$
puis
$$ u_n=v_n-\left(v_{2n}-\dfrac{u_{4n}}{4}\right)=v_n-\dfrac{v_{2n}}{2}+\dfrac{u_{4n}}{4}=v_n-\dfrac{v_{2n}}{2}+\dfrac{v_{4n}}{4}-\dfrac{u_{8n}}{8}.$$
On peut alors montrer par récurrence sur $k\in \N$, que
$$\forall k\in \N,\quad u_n=\dsum_{j=0}^k(-1)^k\dfrac{v_{2^jn}}{2^j}+(-1)^{k+1}\dfrac{u_{2^{k+1}n}}{2^{k+1}}.$$
On en déduit, pour tout $n\in \N,\, k\in \N$,
$$\norme{u_n}=\norme{\dsum_{j=0}^k(-1)^k\dfrac{v_{2^jn}}{2^j}+(-1)^{k+1}\dfrac{u_{2^{k+1}n}}{2^{k+1}} }\leq \dsum_{j=0}^k\dfrac{\norme{v_{2^jn}}}{2^j}+\dfrac{\norme{u_{2^{k+1}n}}}{2^{k+1}}$$
Soit $\varepsilon>0$. La suite $(v_n)$ converge vers $0$, donc il existe $n_0$ tel que, pour tout $n\geq n_0$, $\norme{v_n}\leq \dfrac{\varepsilon}{2}$.
La suite $(u_n)$ est bornée, donc il existe $M>0$ tel que pour tout $n$, $\norme{u_n}\leq M$, puis la suite $(\frac{M}{2^k})_k$ converge vers $0$, en particulier, il existe $k_0$ tel que pour tout $k\geq k_0$, $\dfrac{M}{2^{k+1}}\leq \dfrac{\varepsilon}{2}$.
En utilisant les relations précédente, on trouve pour $n\geq n_0,\, k\geq k_0$, $$\norme{u_n}\leq \dsum_{j=0}^k\dfrac{\norme{v_{2^jn}}}{2^j}+\dfrac{\norme{u_{2^{k+1}n}}}{2^{k+1}}\leq \dfrac{\varepsilon}{2} \dsum_{j=0}^k\dfrac{1}{2^j}+\dfrac{M}{2^{k+1}}\leq \dfrac{\varepsilon}{2} +\dfrac{\varepsilon}{2} =\varepsilon.$$ Ce qui implique que $u_n\tendversN\,0$. -
Supposons que $v_n\tendversN\,\ell$ alors $w_n=v_n-\ell \tendversN\,0$.
Soit $n\geq 0$, on écrit, $$w_n=v_n-\ell=u_n+\dfrac{u_{2n}}{2}-(\dfrac{2\ell}{3}+\dfrac{2\ell}{2\times 3})=(u_n-\dfrac{2\ell}{3})+\dfrac{u_{2n}-\dfrac{2\ell}{3}}{2},$$ comme la suite $(u_n)$ est bornée, il en va de même pour la suite $(u_n-\dfrac{2\ell}{3})$.
On utilise alors le résultat de la question précédente, ce qui donne, $$u_n-\dfrac{2\ell}{3}\tendversN\,0\Longrightarrow u_n\tendversN\,\dfrac{2\ell}{3}.$$
On considère les matrices suivantes: $A=\begin{pmatrix} 1/2&0&0\\ 0&3/5&0\\0&0&1/3 \end{pmatrix},\,\,B=\begin{pmatrix} 1&0&0\\0&-1&1\\0&0&1 \end{pmatrix}$.
- Montrer que la suite $\left(A^n\right)_{n\in \N}$ converge dans $\MM_3(\R)$ et déterminer sa limite.
- Montrer que la suite $\left(B^n\right)_{n\in \N}$ diverge.
- La matrice $A$ est une matrice diagonale, donc d'après le cours, $$A^n=\begin{pmatrix} (1/2)^n&0&0\\ 0&(3/5)^n&0\\ 0&0&(1/3)^n \end{pmatrix}\tendversN\, \begin{pmatrix} 0&0&0\\ 0&0&0\\ 0&0&0 \end{pmatrix}.$$
- Commençons par calculer $B^2$, $$B^2= \begin{pmatrix} 1&0&0\\0&-1&1\\0&0&1 \end{pmatrix}\begin{pmatrix} 1&0&0\\0&-1&1\\0&0&1 \end{pmatrix} =\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1 \end{pmatrix}=I_3.$$ On en déduit que $$\forall n\in \N,\quad B^{2n+1}=B,\quad B^{2n}=I_3$$ Comme $B\neq I_3$, alors $(B^n)$ ne converge pas dans $\MM_3(\R)$.
On considère la matrice $A=\begin{pmatrix} 1&0&0\\ -2&3&1\\ 4&-4&-1 \end{pmatrix}$.
- Calculer $(A-I_3)^2$, en déduire $A^n$, pour $n\in \N$.
- Montrer que la suite $\left(\frac{1}{n} A^n\right)_{n\in \N^*}$ converge et déterminer sa limite.
- Un calcul de $(A-I_3)^2$ donne $$(A-I_3)^2=0\Longrightarrow A^2=2A-I_3\text{ puis } A^3=A (2A-I_3) =2A^2-A=3A-2I_3 ....$$ donc par récurrence sur $n\in \N^*$, on montre $$\forall n\in \N^*,\quad A^n=nA-(n-1)I_n.$$
- D'après la question précédente, on a $$\forall n\geq 1,\quad \dfrac{1}{n}A^n=A-\dfrac{n-1}{n}I_3\tendversN\, A-I_3.$$
Soient $A,\,B\in \MM_p(\R)$. On suppose que $(AB)^n\tendversN\,0_p$. Montrer que $(BA)^n\tendversN\,0_p$.
Il suffit d'écrire, $$\forall n\geq 2,\quad (BA)^n = (BA) (BA)\cdots (BA)(BA) =B(AB)(AB)\cdots (AB)B=A (AB)^{n-1} B$$ Comme $(AB)^n\tendversN\,0_p$ alors $(AB)^{n-1}\tendversN\,0_p$ ce qui donne le résultat.
Soit~$B\in\MM_n(\R)$ une matrice antisymétrique, telle que la suite~$\bigl(B^n\bigr)_{n\in\N}$ converge vers une matrice~$C$. Que peut-on dire de~$C$ ?
Pour tout $n\in \N$, on a $\left( \,^tB\right)^n=\,^t (B^n)\tendversN \,^t C$. Comme $B$ est antisymétrique alors $\,^tB=-B$ donc $\left( \,^tB\right)^n=(-B)^n$ donc $$\left( \,^tB\right)^{2n}=B^{2n}\tendversN\,C,\text{ et } \left( \,^tB\right)^{2n+1}=-B^{2n+1}\tendversN\,-C.$$ Donc $C=-C$ d'où $C=0$.
Soit $M\in \MM_n(\K)$, on suppose que la suite $(M^n)$ converge vers $A\in \MM_n(\K)$.
- Montrer que la suite $\left((M^2)^n\right)_n$ converge dans $\MM_n(\K)$.
- Montrer que $A^2=A$.
La suite $(M^n)_n$ converge donc toute suite extraite de cette suite converge aussi (vers la même limite), en particulier, la suite $(M^{2n})_n$ converge aussi vers $A$ . Pour tout $n\in \N$, on a $M^{2n}=M^n\times M^n$ ainsi par passage à la limite on trouve $A= A\times A$.
Soit $E$ un $\K$-evn de dimension finie $p$, et $(x_n)$ une suite d'éléments de $E$. On suppose que $\dsum \norme{x_n}$ converge dans $\R$, montrer que $\dsum x_n$ converge dans $E$.
Soit $\BB=(e_1,\cdots,e_p)$ une base de $E$, pour tout $n\in \N$, on a
$x_n=x_{1,n}e_1+x_{2,n}+\cdots+x_{p,n}e_p$
($(x_{i,n})_n$ est la $i$\up{ème} suite cordonnée de $(x_n)$ relativement à la base
$\BB$).
$E$ étant de dimension finie, donc tout les normes sur $E$ sont équivalentes, on travaille
donc avec la norme
infinie définie par $\norme{\dsum_{k=1}^p a_ke_k}=\max\{\abs{a_k},\,k\in\inter{1,p}\}$.
On a pour tout $i\in \inter{1,p}$ et $n\in \N$, $\abs{x_{i,n}}\leq \norme{x_n}_\infty$, or
$\dsum \norme{x_n}_\infty$ converge. On en déduit alors que $\dsum x_{i,n}$ est absolument
convergente donc convergente. Notons $\ell_i$ sa somme.
$$\forall n\in \N,\quad \dsum_{k=0}^nx_k=\dsum_{k=0}^n (\dsum_{i=1}^p
x_{i,k}e_i)=\dsum_{i=1}^p\left(\dsum_{k=0}^nx_{i,k}\right)e_i\tendversN\,\dsum_{i=1}^p\ell_i
e_i.$$
Soit $A\subset E$ un ensemble non vide. On suppose que $A$ est convexe. Montrer que $\overline{A}$ est convexe.
Soient $x,y\in \overline{A}$ et $\lambda\in ]0,1[$, d'après la proposition précédente, ils existe deux suites $(x_n),\, (y_n)$ d'éléments de $A$ tels que $x_n\tendversN\,x$ et $y_n\tendversN \,y$. On considère alors la suite $(w_n)$ définie par $w_n=\lambda x_n+(1-\lambda)y_n$. Alors la suite $(w_n)$ vérifie: $$\forall n\in \N,\,w_n\in A \text{ (car $A$ est convexe) et }w_n\tendversN\,\lambda x+(1-\lambda)y.$$ Puisque $(w_n)\in A^\N$ alors $\lim w_n\in \overline{A}$, ceci prouve que $\lambda x+(1-\lambda)y\in \overline{A}$.
Soit $E=\CC([0,1],\R)$ muni de la norme $\norme{\cdot}_\infty$. On note $$A=\{f\in E,\, f(0)=0 \text{ et }\dsp\int_0^1f(t)\ud t\geq 1\}.$$ Montrer que $A$ est une partie fermée de $E$.
Soit $(f_n)$ une suite d'éléments de $A$ qui converge dans $E$ vers $f$, i.e. $\norme{f_n-f}_\infty\tendversN\,0$.
- Pour tout $n\in \N$, on a $$\abs{f_n(0)-f(0)}\leq \norme{f_n-f}_\infty\Longrightarrow\abs{f(0)}\leq \norme{f_n-f}_\infty\tendversN 0$$ Donc $f(0)=0$.
- En utilisant les propriétés de l'intégrale, $$\abs{\int_0^1(f-f_n)}\leq \int_0^1\norme{f-f_n}_\infty\leq \norme{f-f_n}_\infty\Longrightarrow \int_0^1f_n(t)\ud t\tendversN\,\int_0^1f(t)\ud t$$ or pour tout $n\in \N,\,\dsp\int_0^1 f_n\geq 1$ donc $\dsp\int_0^1 f(t)\ud t\geq 1$
On en déduit alors que $f\in A$, ce qui prouve que $A$ est un fermé de $E$.