Suites et séries de fonctions
Dans ce chapitre $I$ désigne un intervalle de $\R$ non vide et non réduit à un point. $\K$ désigne
$\R$ ou
$\C$. Enfin on note $\mathcal{F}(I,\K)$ désigne l'ensemble des fonctions définies sur $I$ à valeur
dans $\K$.
On note également $\Bb(I,\K)$ l'ensemble des fonctions définies sur $I$ et bornées sur $I$.
On rappelle que:
- $\mathcal{F}(I,\K)$ est un $\K$ espace vectoriels pour les opérations usuelles.
- $\Bb(I,\K)$ est un sous espace vectoriel de $\mathcal{F}(I,\K)$.
- L'application $\norme{}_\infty:\Bb(I,\K)\mapsto \R_+$ définie par $\norme{f}_\infty=\dsp\sup_{x\in I}\abs{f(x)}$, définit une norme sur $\Bb(I,\K)$ (appelée norme de la convergence uniforme).
Suites de fonctions
Considérons pour commencer, une équation différentielles
$$f(0)=x_0\in \K,\quad f'(t)=\varphi(t,f(t)).$$
avec $f:I\longmapsto \K$ et $\varphi:I\times \K\longmapsto \K$ supposé dans notre cas assez
régulier.
L'étude de ce problème, pose pas mal de difficultés. L'existence de solution? Trouver la solution?
ou trouver une approximation de la solution.
On peut remarquer que si $f$ est une solution, alors,
$$\forall t\in I,\, f(t)=f(t_0)+\int_{t_0}^tf'(s)\ud s= x_0+ \int_{t_0}^t\varphi(s,f(s))\ud s.$$
Il est donc naturelle, de définir une suite de fonctions de la façon suivante:
$$f_0(t)=x_0,\quad \forall k\in \N,\quad f_{k+1}(t)=x_0+ \int_{t_0}^t\varphi(s,f_k(s))\ud s.$$
La suite $(f_n)$ est bien définie, et on peut espérer qu'elle converge vers une fonction $g$ et que
ce dernier
soit une solution de $(E)$. Mais
- Quelle définition peut-on donner de la convergence de la suite $f_n$? Par rapport à quelle norme?
- S'il y convergence, la fonction limite est-t-elle dérivable?
- La limite éventuelle de cette suite est-elle compatible avec l'intégrale, i.e. $$\lim\int \varphi(t,f_n(t))\ud t \overset{?}{=}\int \varphi( t,\lim f_n(t))\ud t.$$
Convergence simple, uniforme
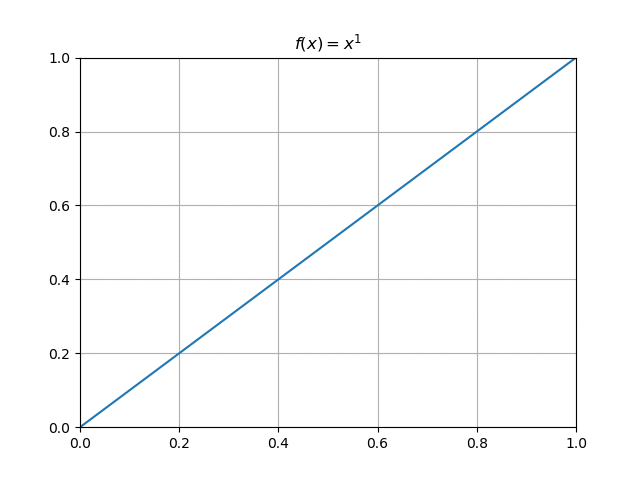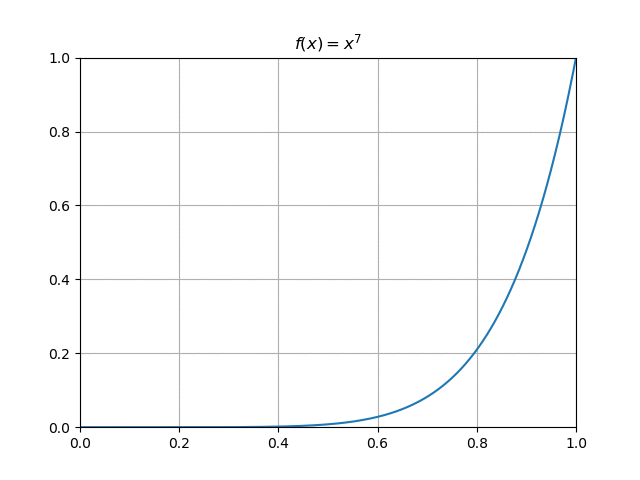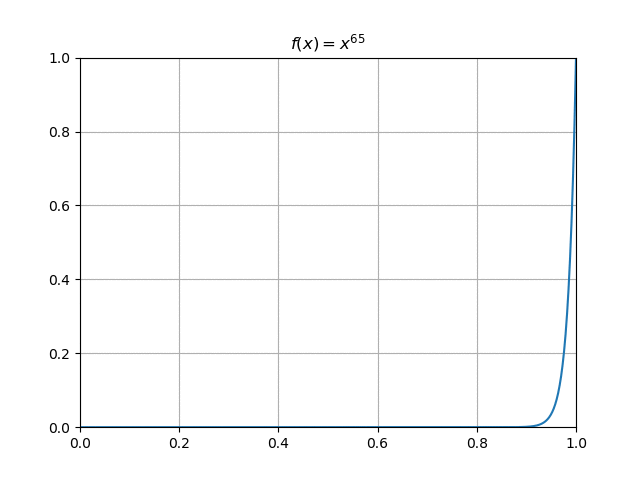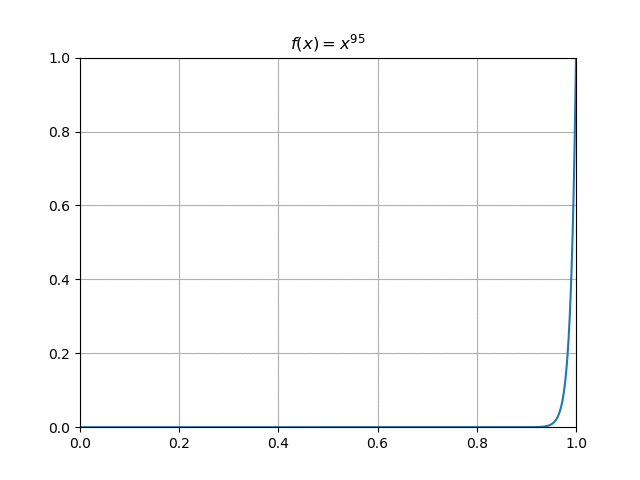
Soit, pour $n\in \N$, $\fonct{f_n}{[0,1]}{\R}{x}{x^n}$. Étudier la convergence simple de la suite $(f_n)_{n\in \N}$.
Pour $x\in [0,1[$ la suite $(x^n)_n$ converge vers $0$ donc $f_n(x)\tendversN\,0$, tandis que pour $x=1$, on a $f_n(1)=1\tendversN\,1$. Alors la suite $(f_n)$ converge simplement sur $[0,1]$ vers la fonction $f: x \longmapsto \begin{cases}0 & \text{si } x\in [0,1[ \\ 1 & \text{si } x=1 \end{cases}$
La convergence simple sur $I$ d'une suite de fonctions $(f_n)$ vers $f$ peut s'écrire sous la forme $$\forall x\in I, \ \forall \eps>0,\ \exists \underbrace{n_0}_{\substack{\text{dépend de }\eps\\ \text{ et de }x}} \in\N,\ \forall n\in \N,\ n\geq n_0 \Longrightarrow \abs{f_n(x)-f(x)}< \eps$$
La réciproque de ce résultat est faux. comme le montre l'exemple suivant.
Soit, pour $n\in \N$, $\fonct{f_n}{[0,1]}{\R}{x}{x^n}$. Alors la suite $(f_n)$ converge simplement sur $[0,1]$ vers la fonction $f: x \longmapsto \begin{cases}0 & \text{si } x\in [0,1[ \\ 1 & \text{si } x=1 \end{cases}$ Or $\dsp\sup_{x\in [0,1]}\abs{f_n(x)-f(x)}=\dsp\sup_{x\in[0,1[}x^n =1$, donc la suite $(f_n)$ ne converge pas uniformément vers $f$ sur [0,1]. Cependant, il y a convergence uniforme sur tout segment de la forme $[0,a]$ avec $0 \leq a < 1$, puisque $\dsp\sup_{x\in [0,a]}\abs{f_n(x)-f(x)} =a^n$ tend vers $0$ quand $n\longrightarrow +\infty$.
Ainsi, pour montrer la convergence uniforme d'une suite de fonctions $(f_n)$,
- $\mathbf{a) }\,$ On cherche $f$ la limite simple de la suite $(f_n)$, puisque si $(f_n)$ converge uniformément la limite ne peut être que la limite simple de la suite.
- $\mathbf{b) }\,$ On essais ensuite, soit de calculer $\norme{f_n-f}_\infty^I$ lorsque ceci est possible, soit de majorer $\abs{f_n(x)-f(x)}$ par une quantité qui ne doit pas dépendre de $x$ et doit tendre vers $0$ lorsque $n$ tend vers $\infty$. (c.f. exercice suivant).
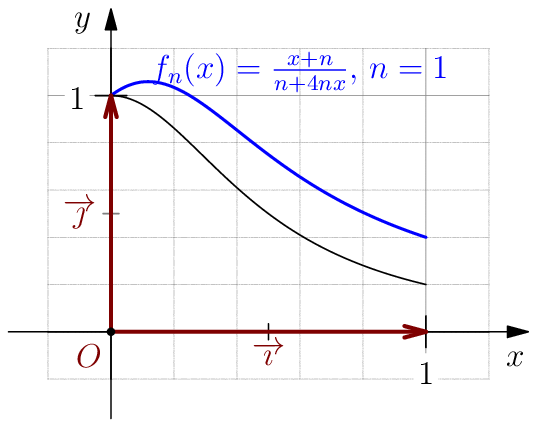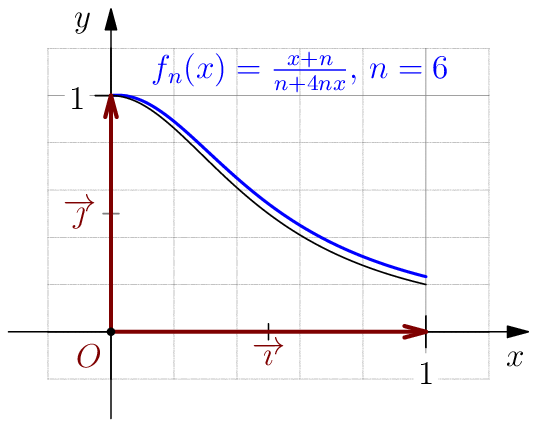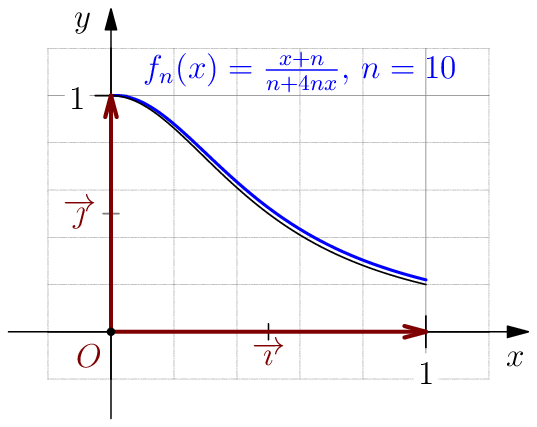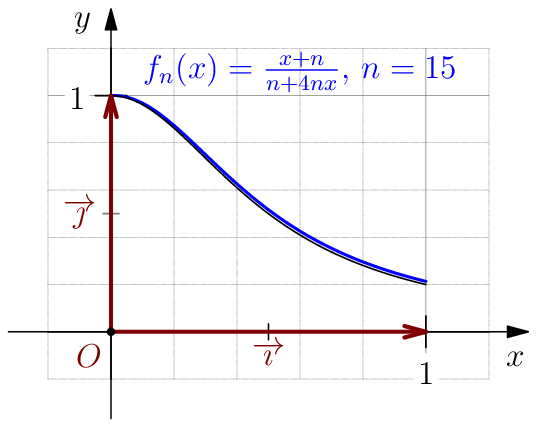
Soit, pour $n\in \N$, $\fonct{f_n}{[0,1]}{\R}{x}{\frac{x+n}{n+4nx^2}}$. Étudier la convergence uniforme de la suite $(f_n)_{n\in \N}$.
Pour $x\in [0,1]$, on a $f_n(x)=\dfrac{1+\frac{x}{n}}{1+4x^2}\tendversN \dfrac{1}{1+4x^2}$. Alors la suite $(f_n)$ converge simplement sur $[0,1]$ vers la fonction $f: x \longmapsto \dfrac{1}{1+4x^2}$. D'autre part, $$\forall x\in [0,1], f_n(x)-f(x)=\dfrac{x}{n(1+4x^2)}\Longrightarrow\dsp\sup_{x\in [0,1]}\abs{f_n(x)-f(x)} \leq \dfrac1n.$$ Donc la suite $(f_n)$ converge uniformément vers $f$ sur $[0,1]$.
Animation en pdf ici
Dans certain cas, il est facile de montrer qu'il n'y a pas de convergence uniforme. Il s'agit de faire un choix approprié de $x$ (en fonction de $n$). Prenons l'exemple: $f_n(x)=\sin (\frac{x}{n})$ il est claire que $f_n$ CS vers $0$ sur $\R$, si on choisit de calculer $f_n(n)$ on trouve $f_n(n)=\sin(1)>0$ ce qui implique qu'il n' y a pas de convergence uniforme.
Montrer la convergence uniforme sur $I$ peut s'avérer une tâche un peu difficile
voir impossible (surtout s'il n'y pas de convergence uniforme), or pour étudier
certaines propriétés de la limite en un point $a\in I$ on a besoin de la convergence uniforme
au voisinage de $a$, ce qui ce passe ailleurs nous nous intéresse pas!
On va alors introduire une nouvelle notions de la convergence:
Ceci équivalent à: pour tout segment $J$ de $I$ la suite $(f_{n\mid _J})$ converge uniformément vers $f_{\mid _J}$.
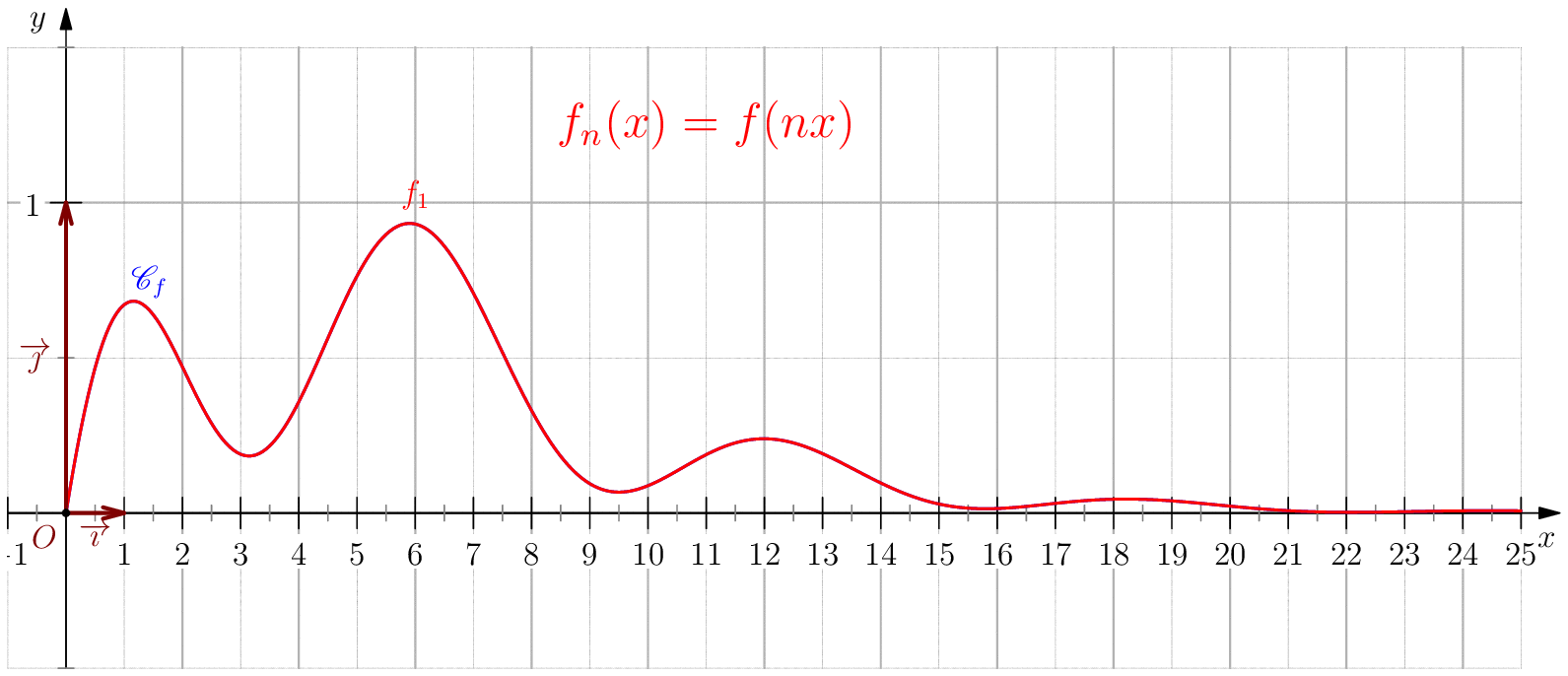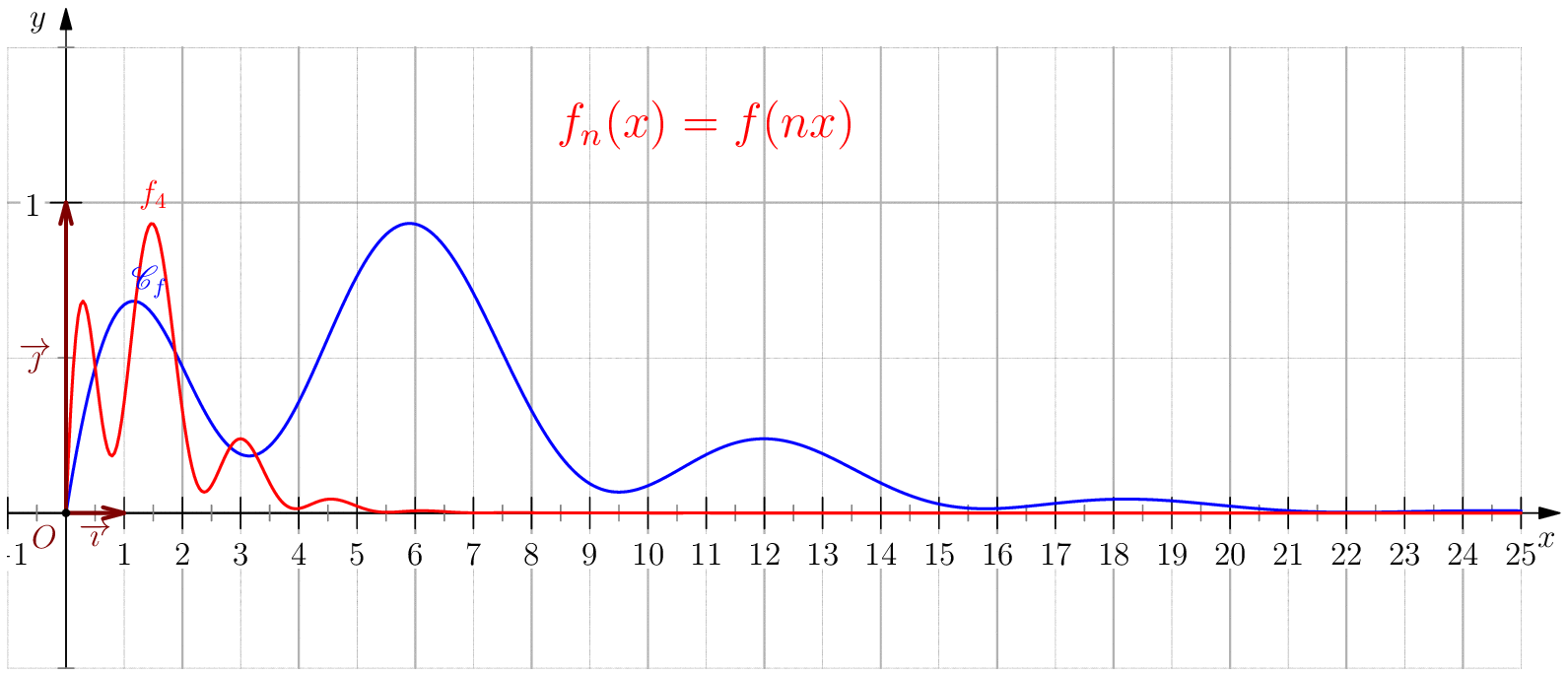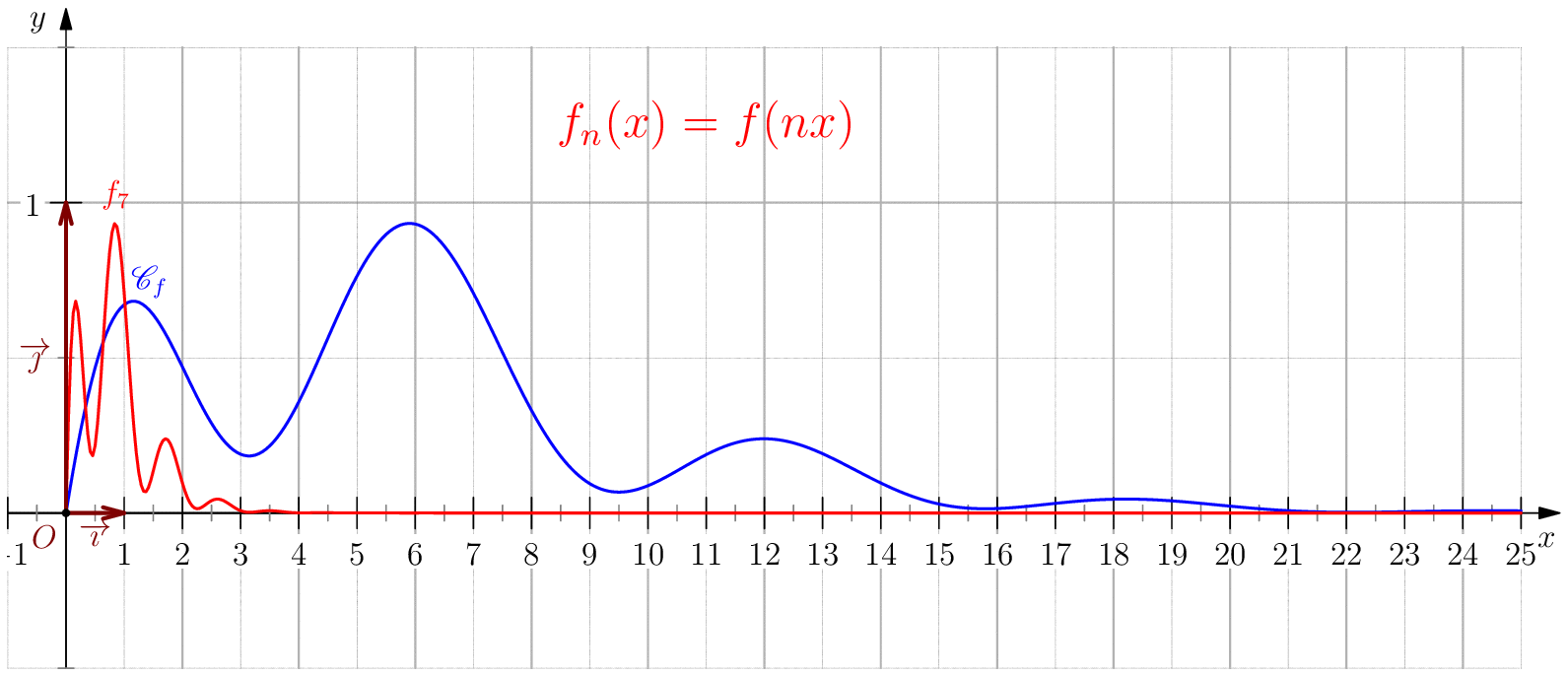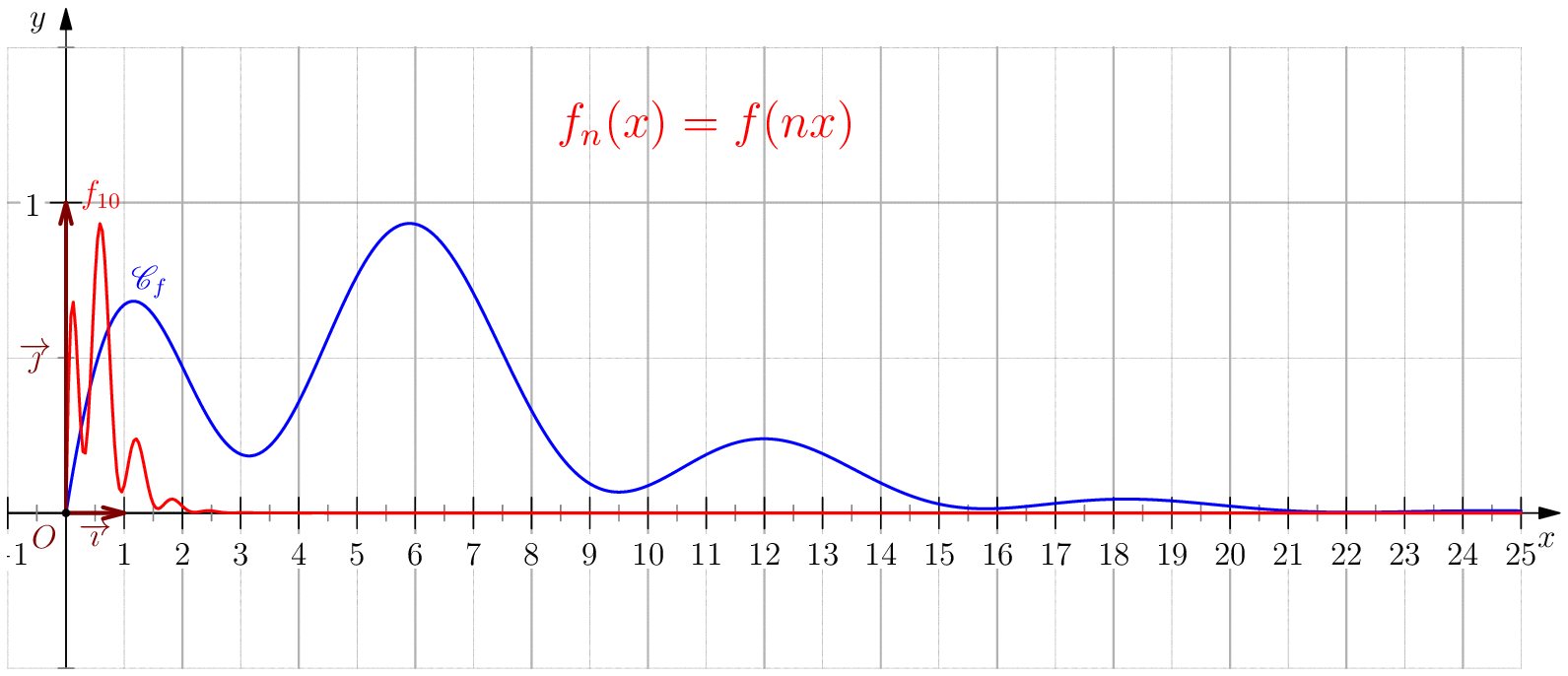
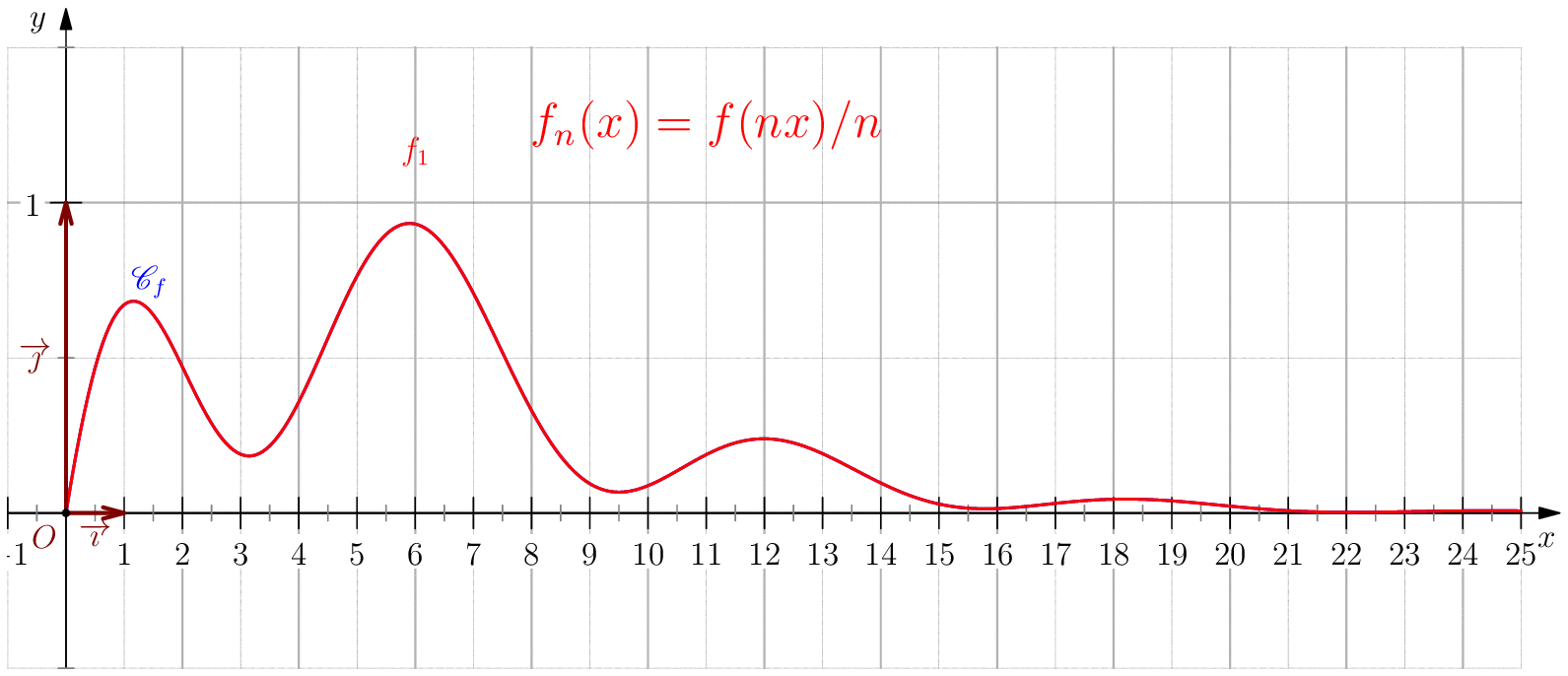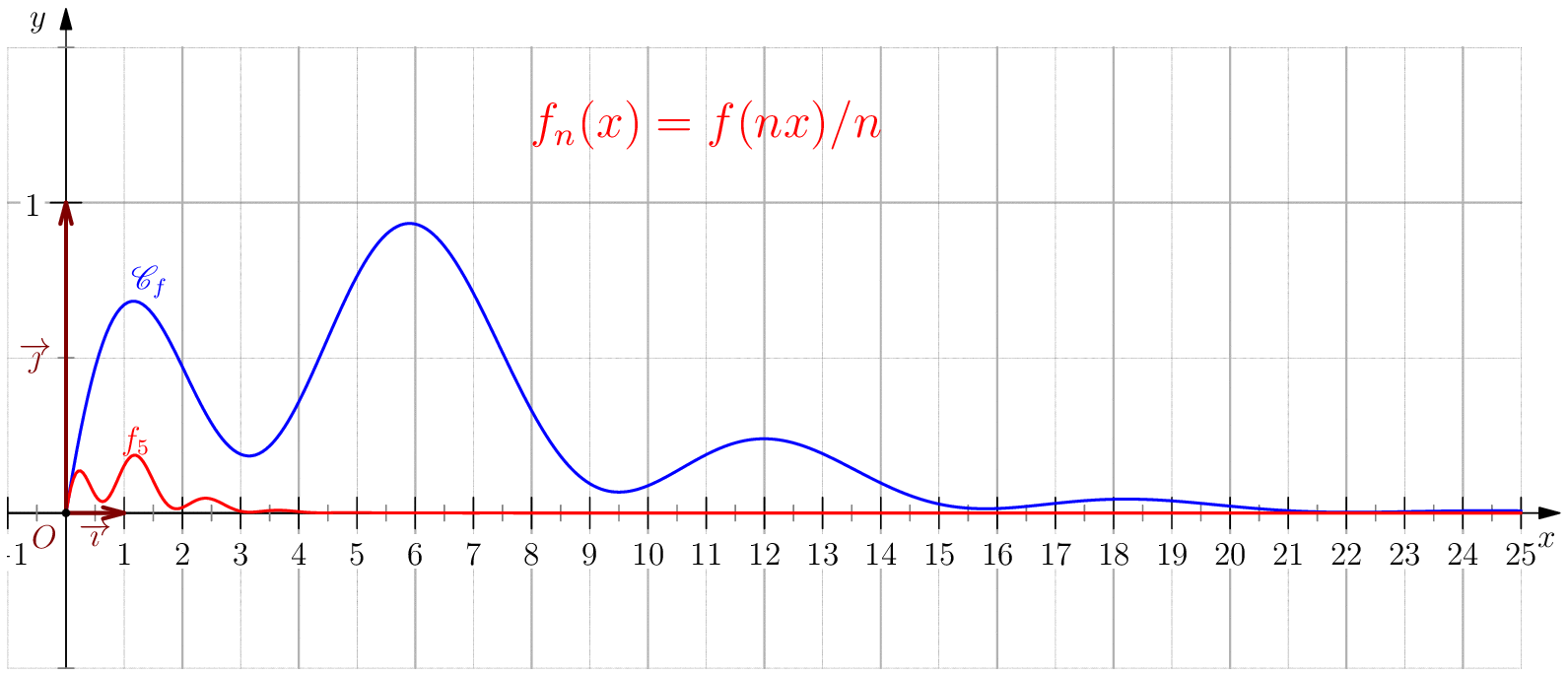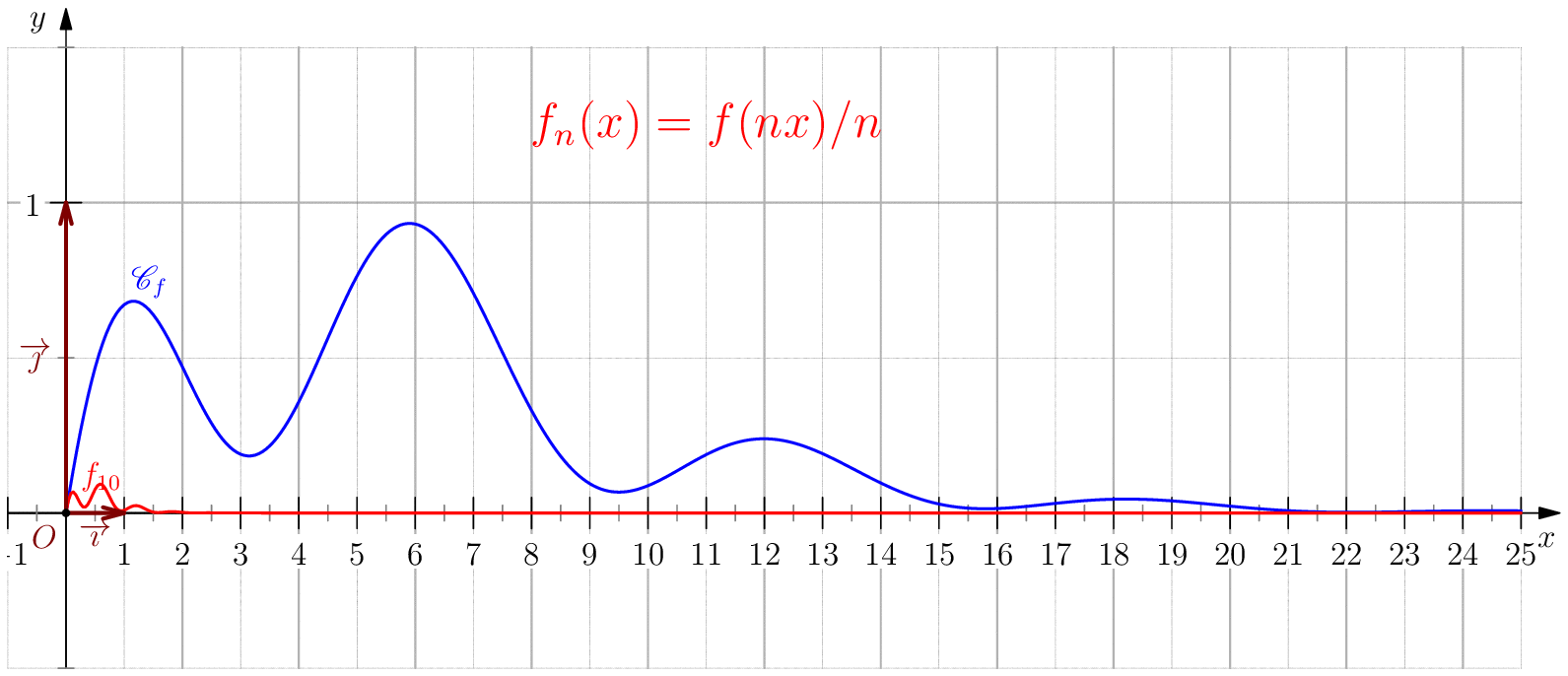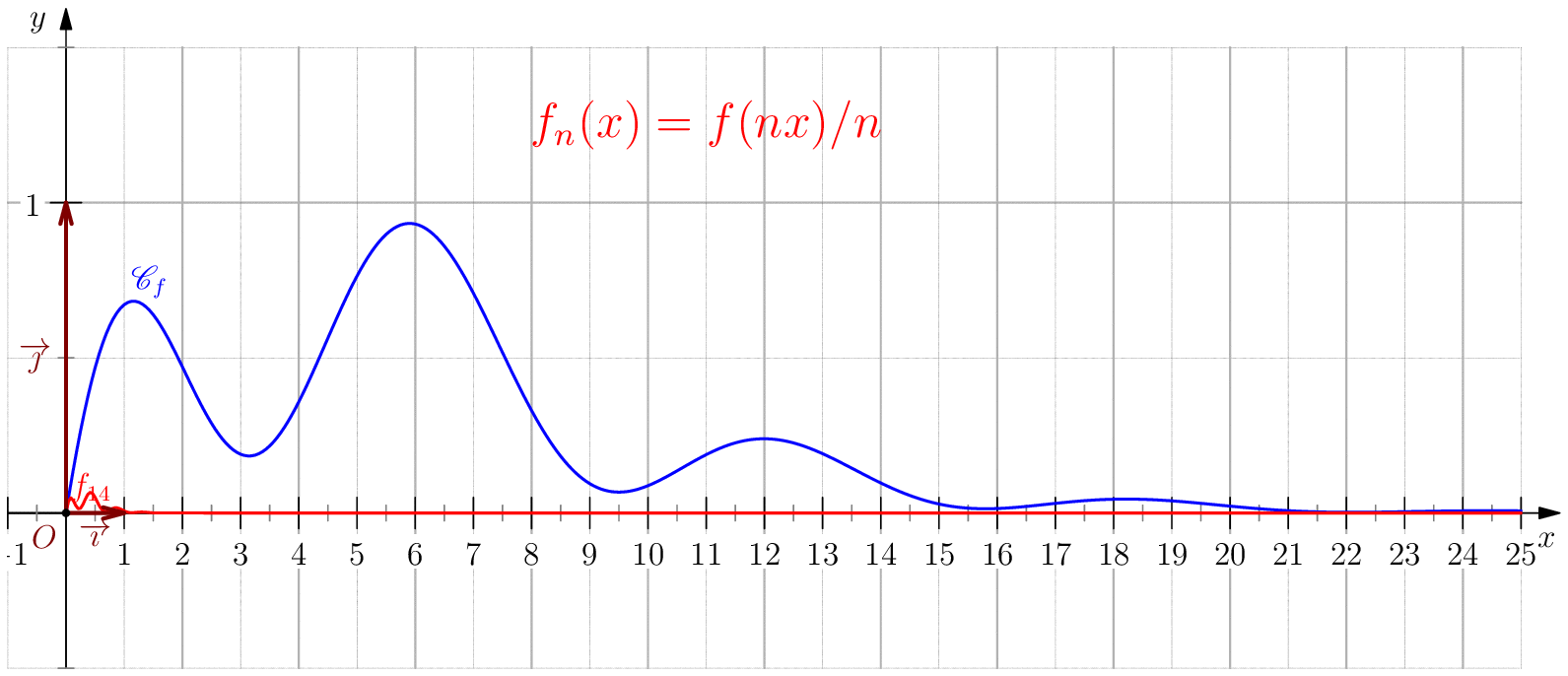
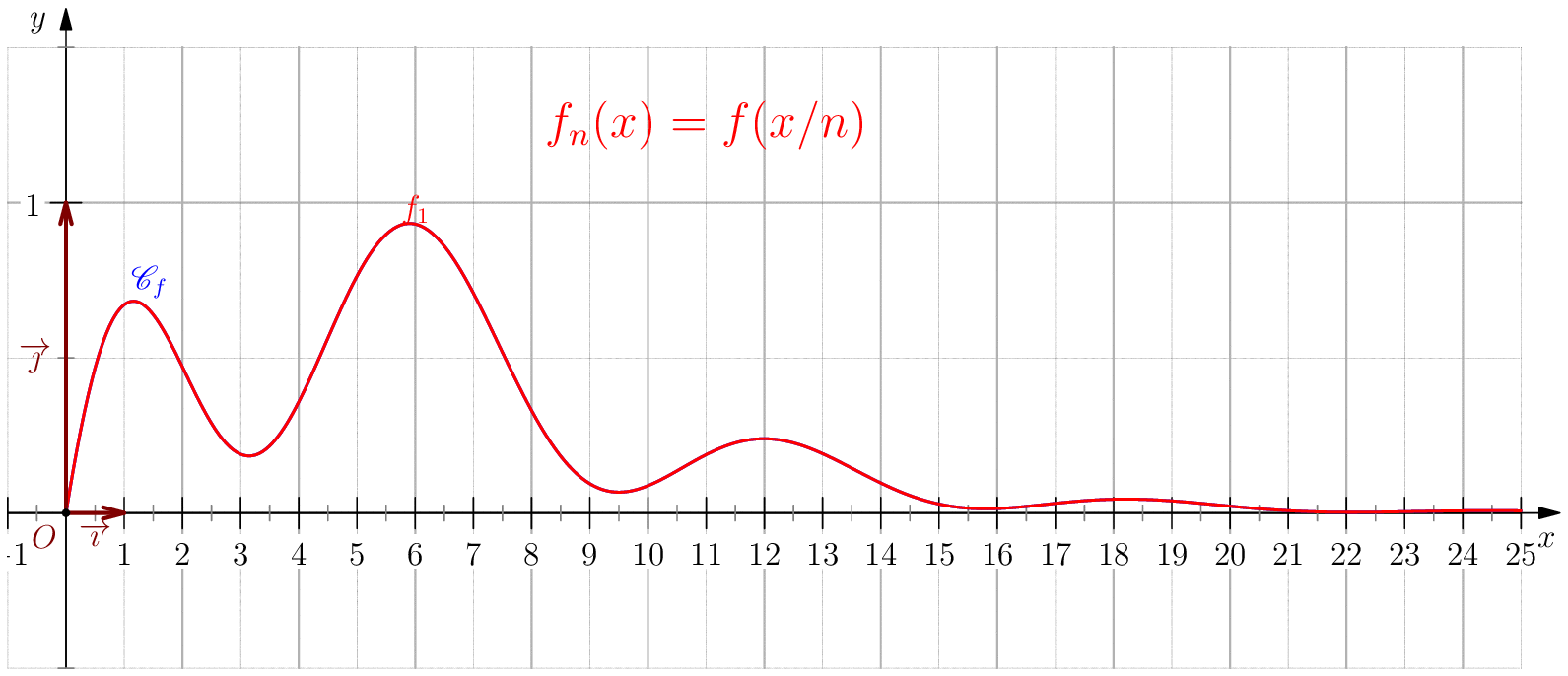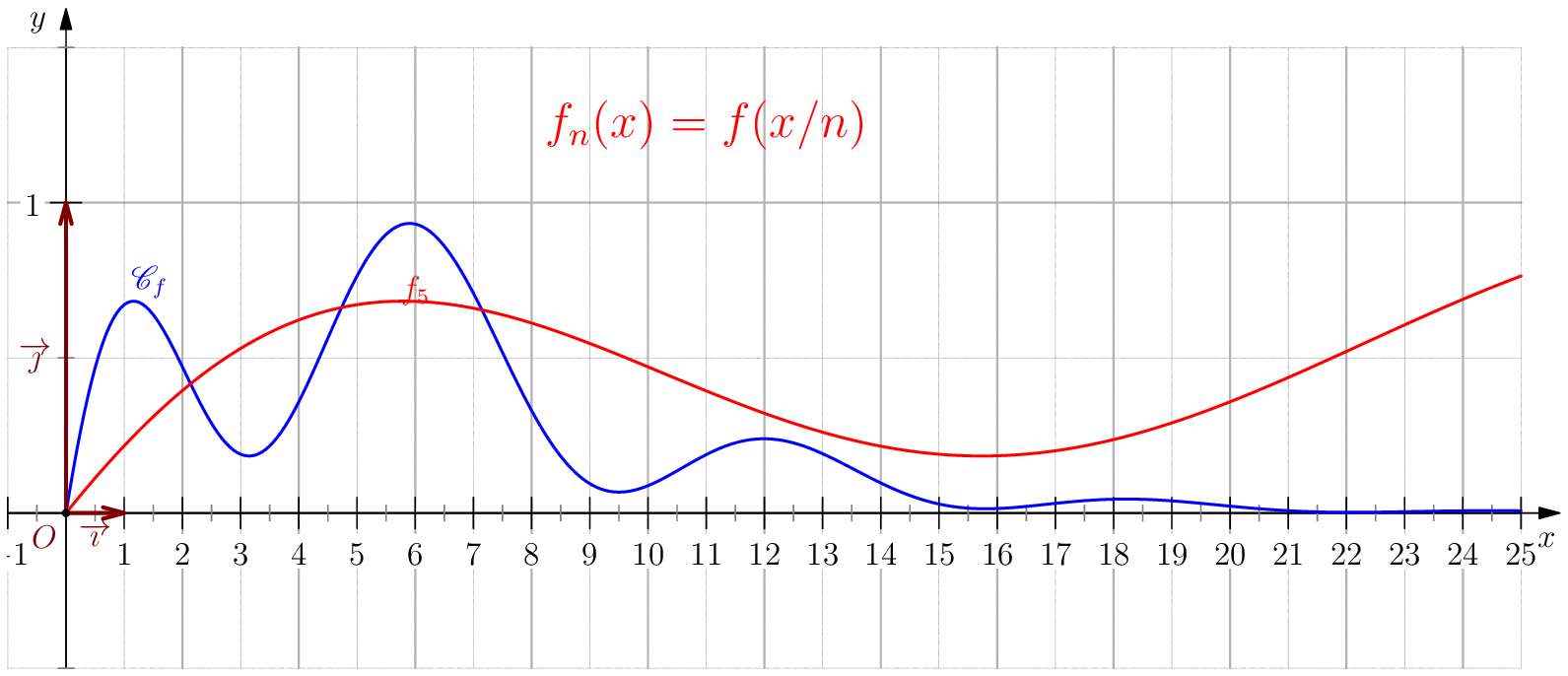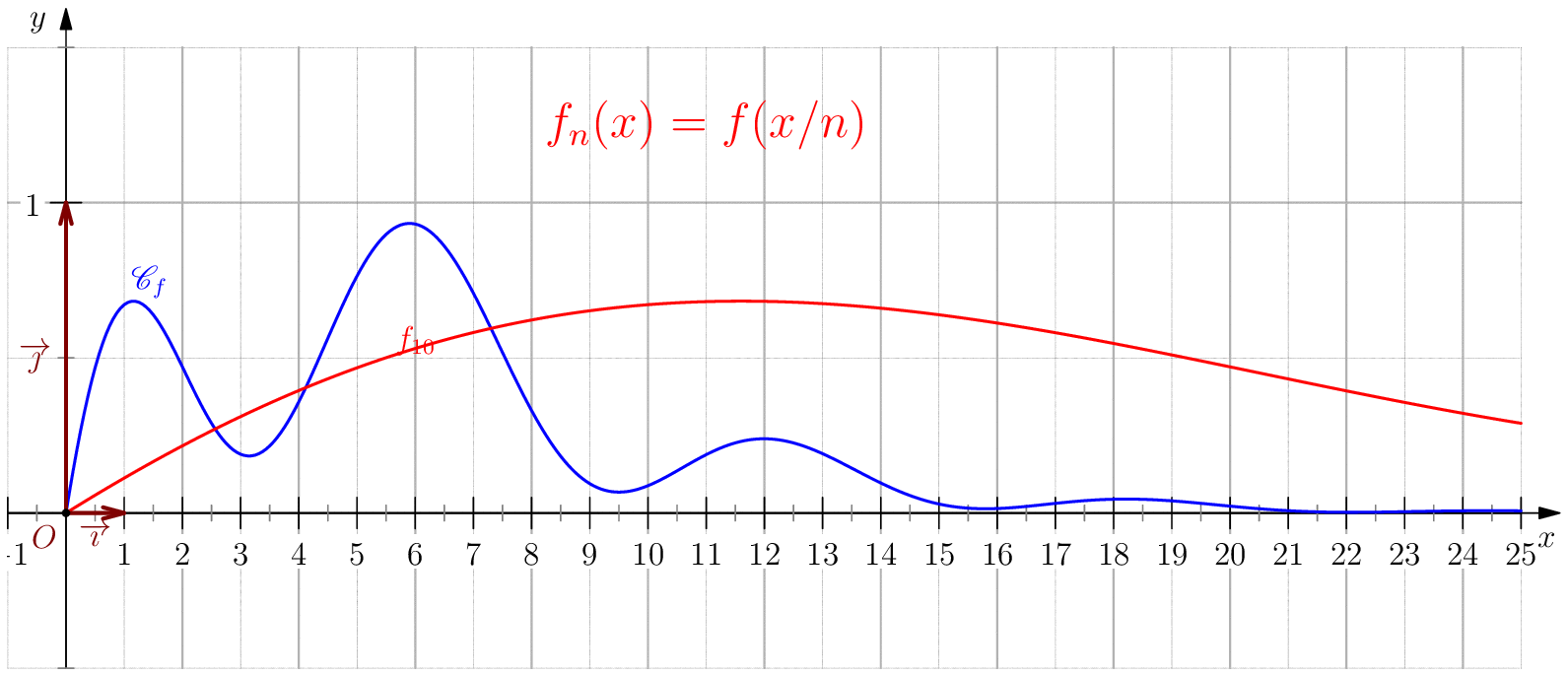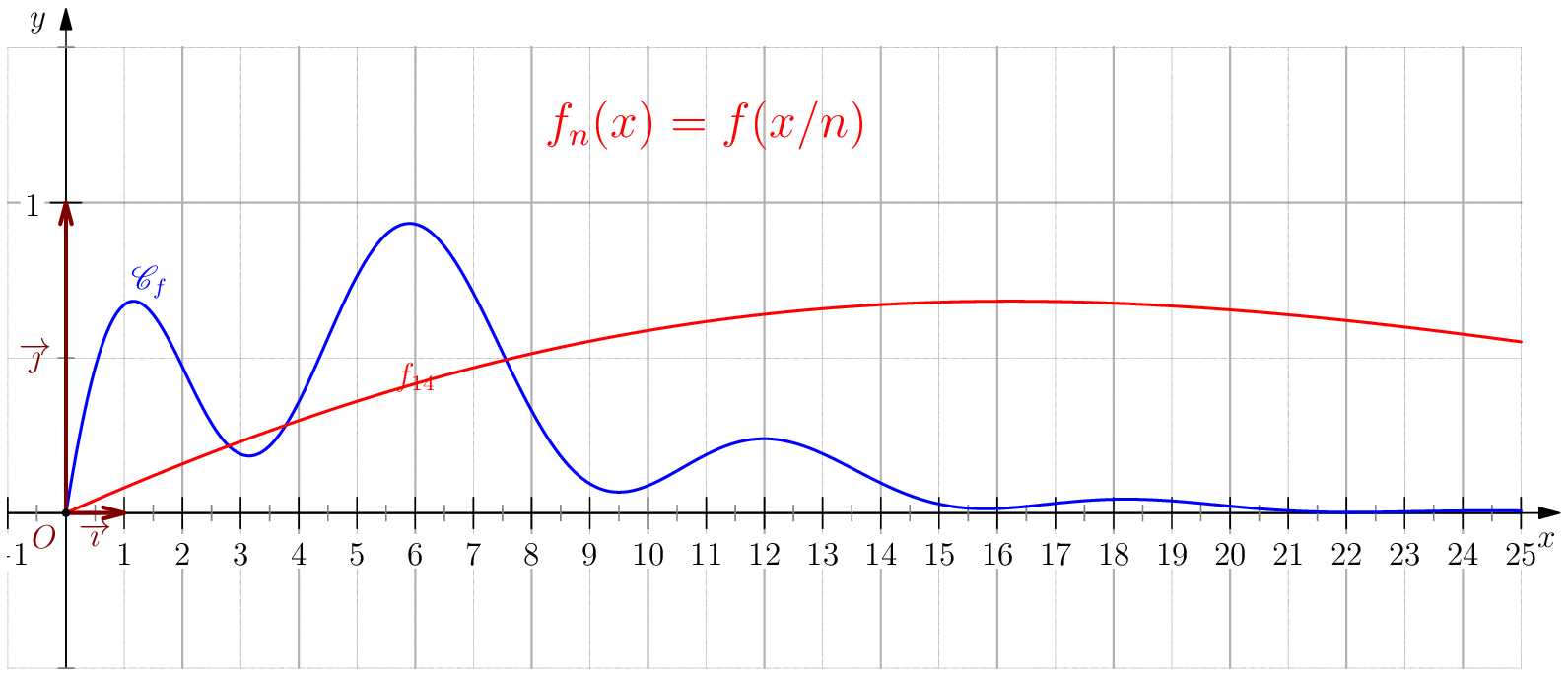
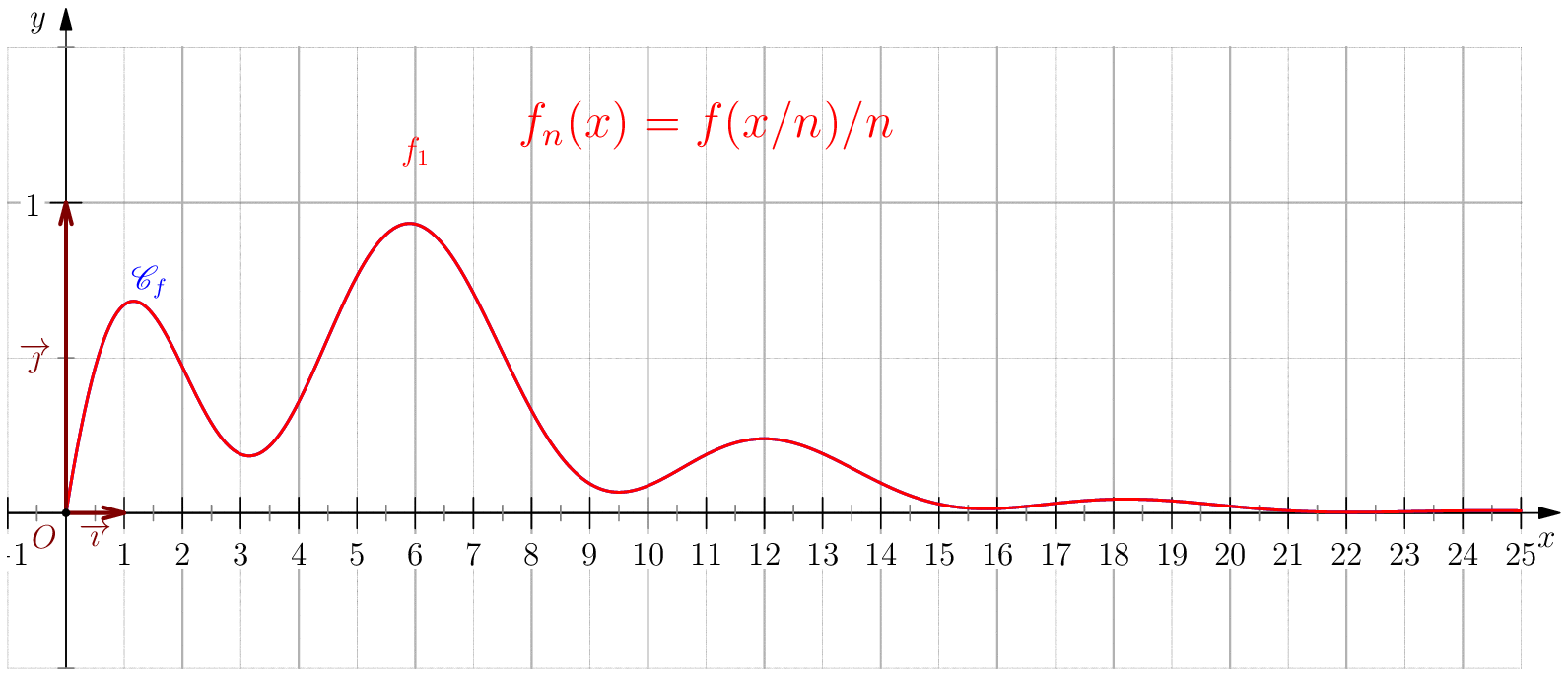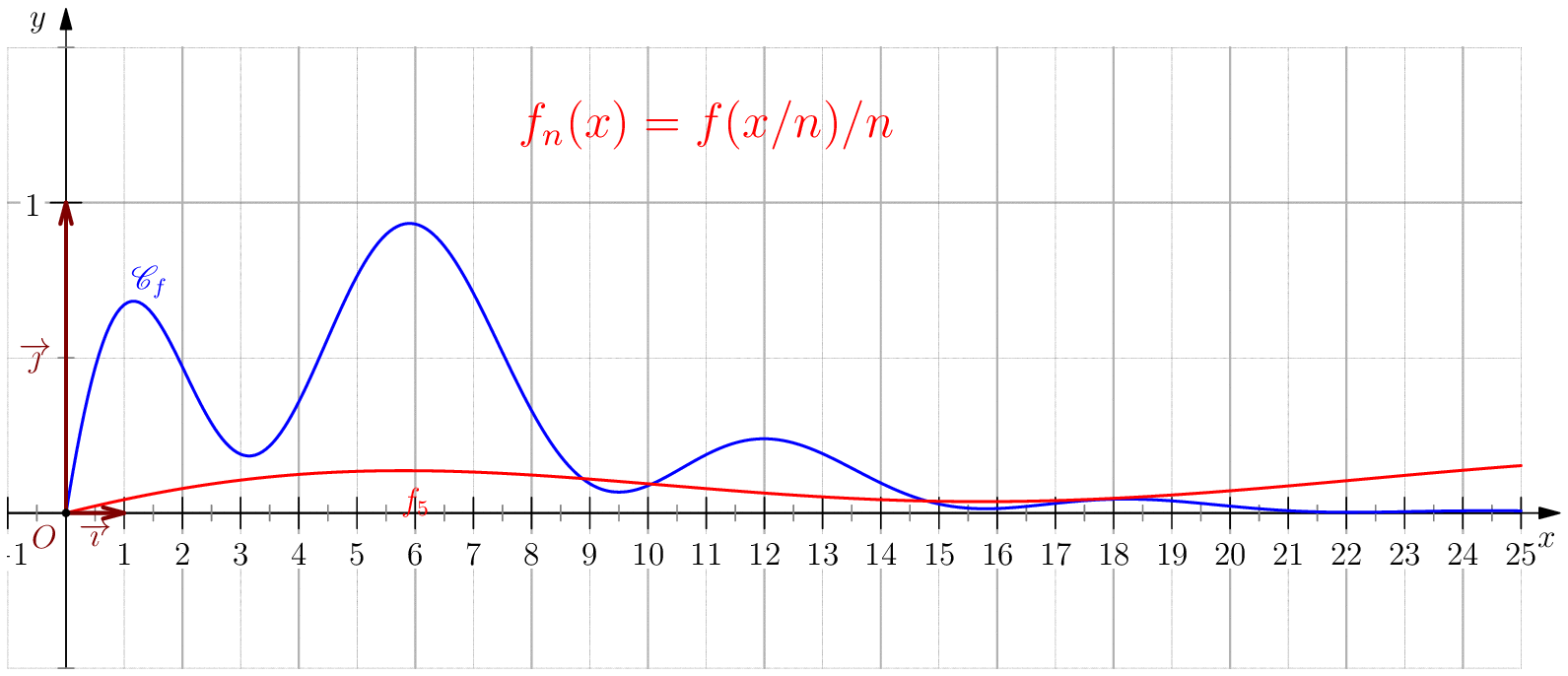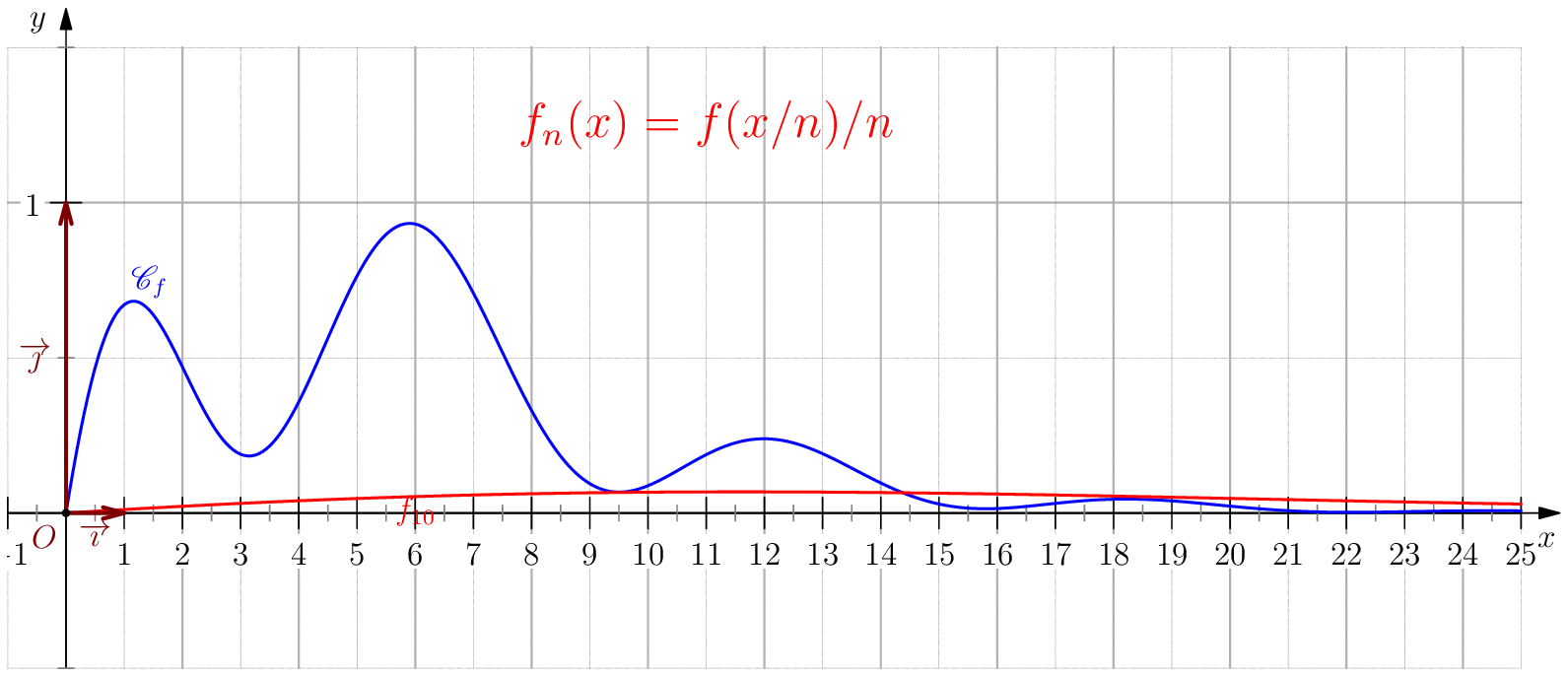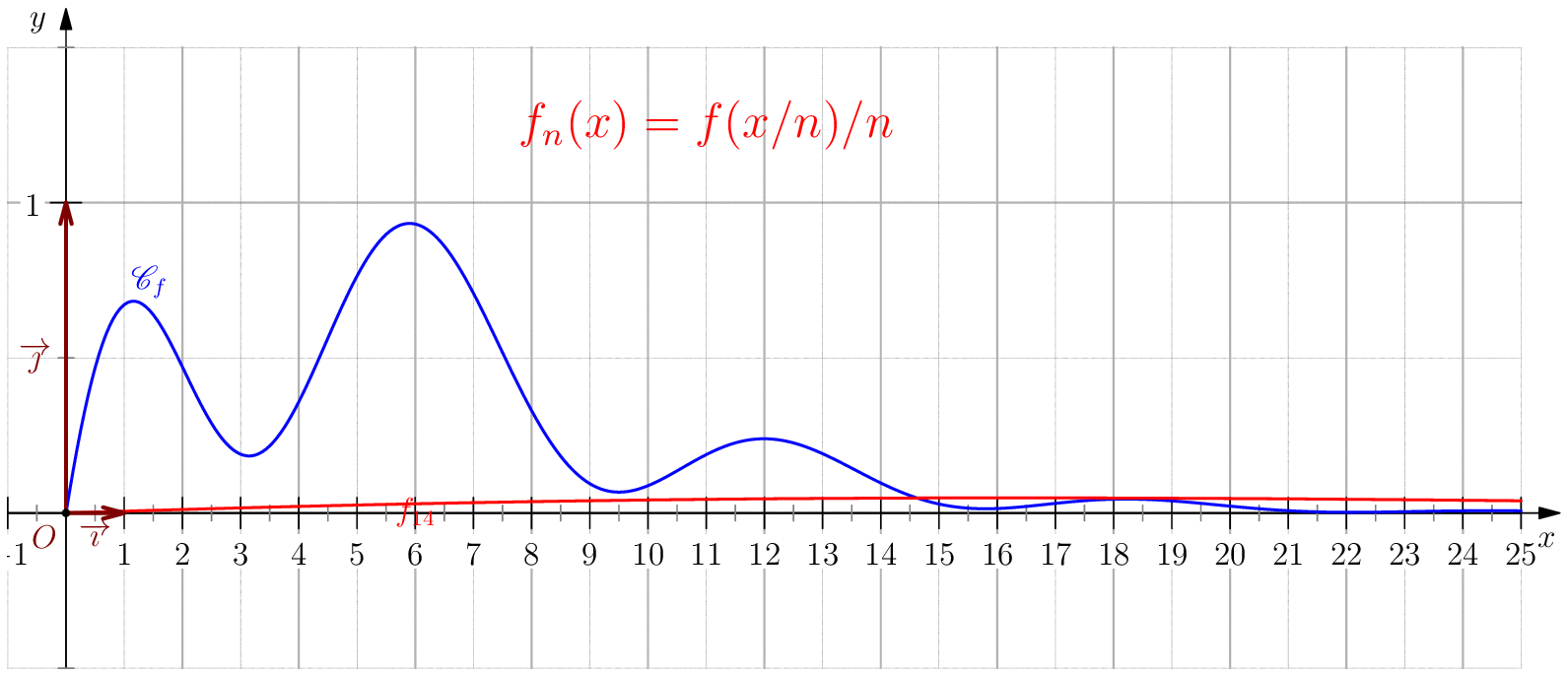
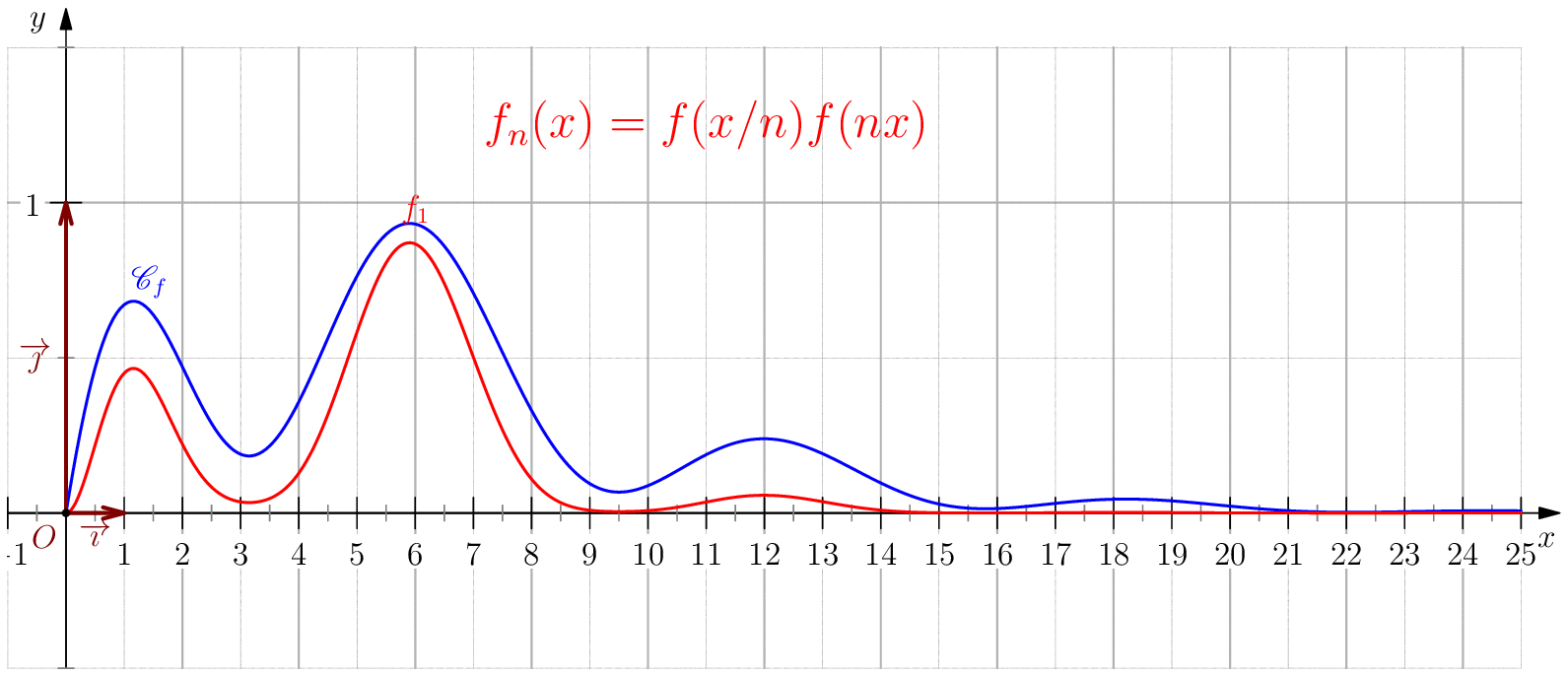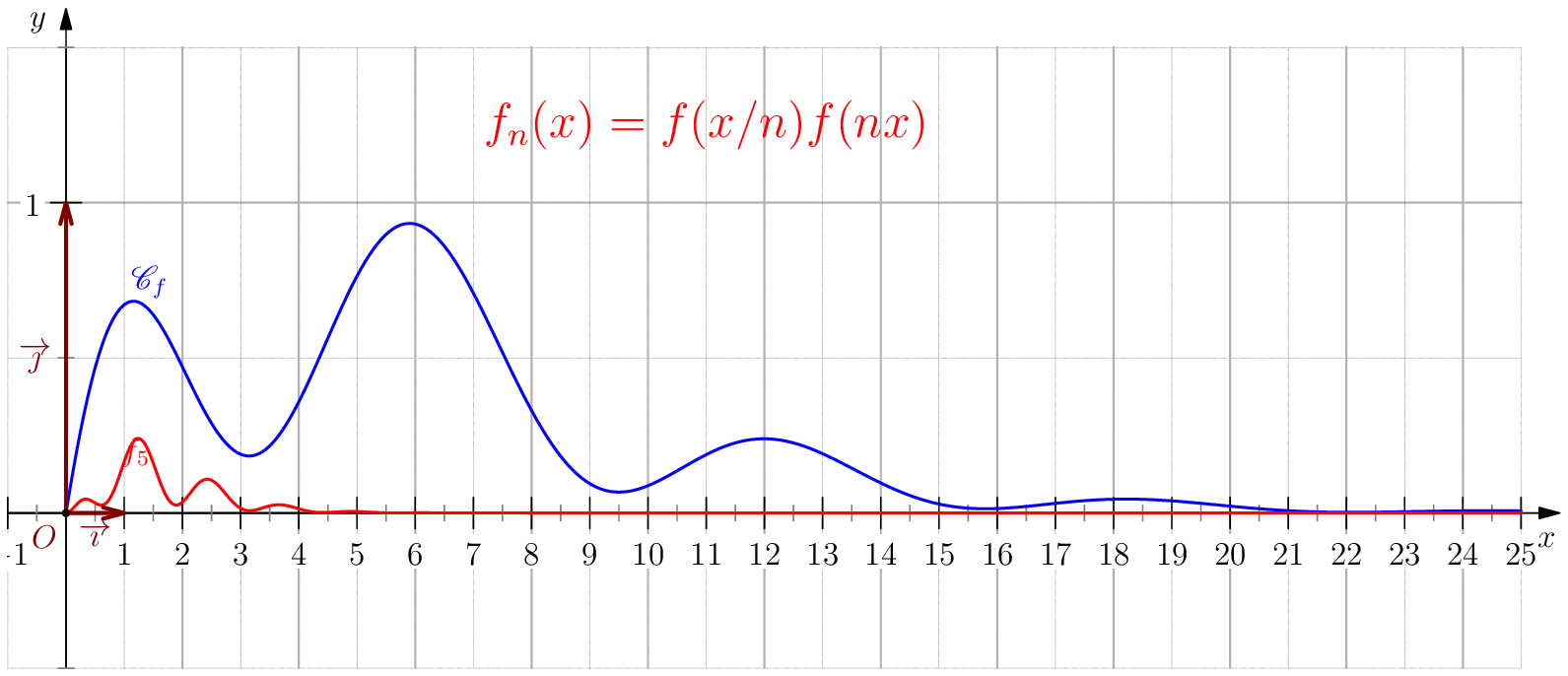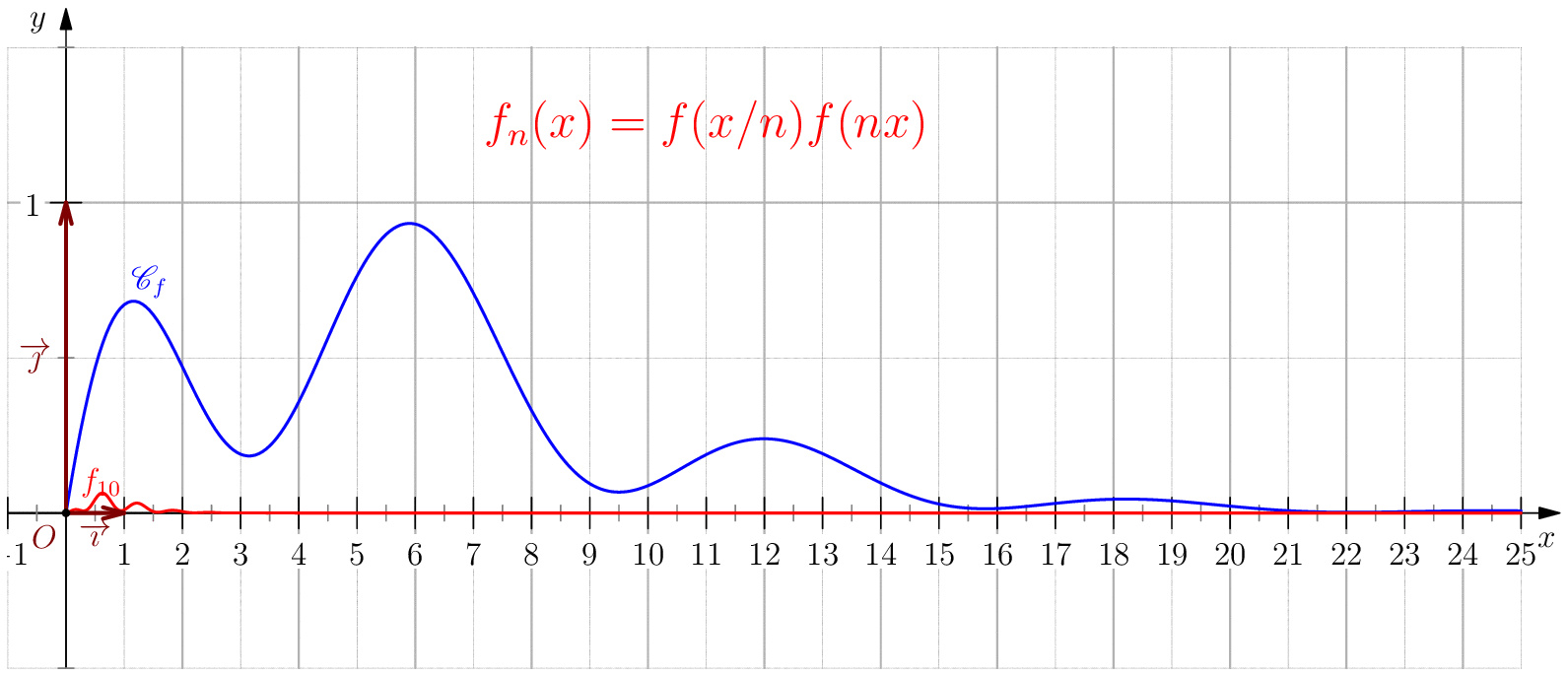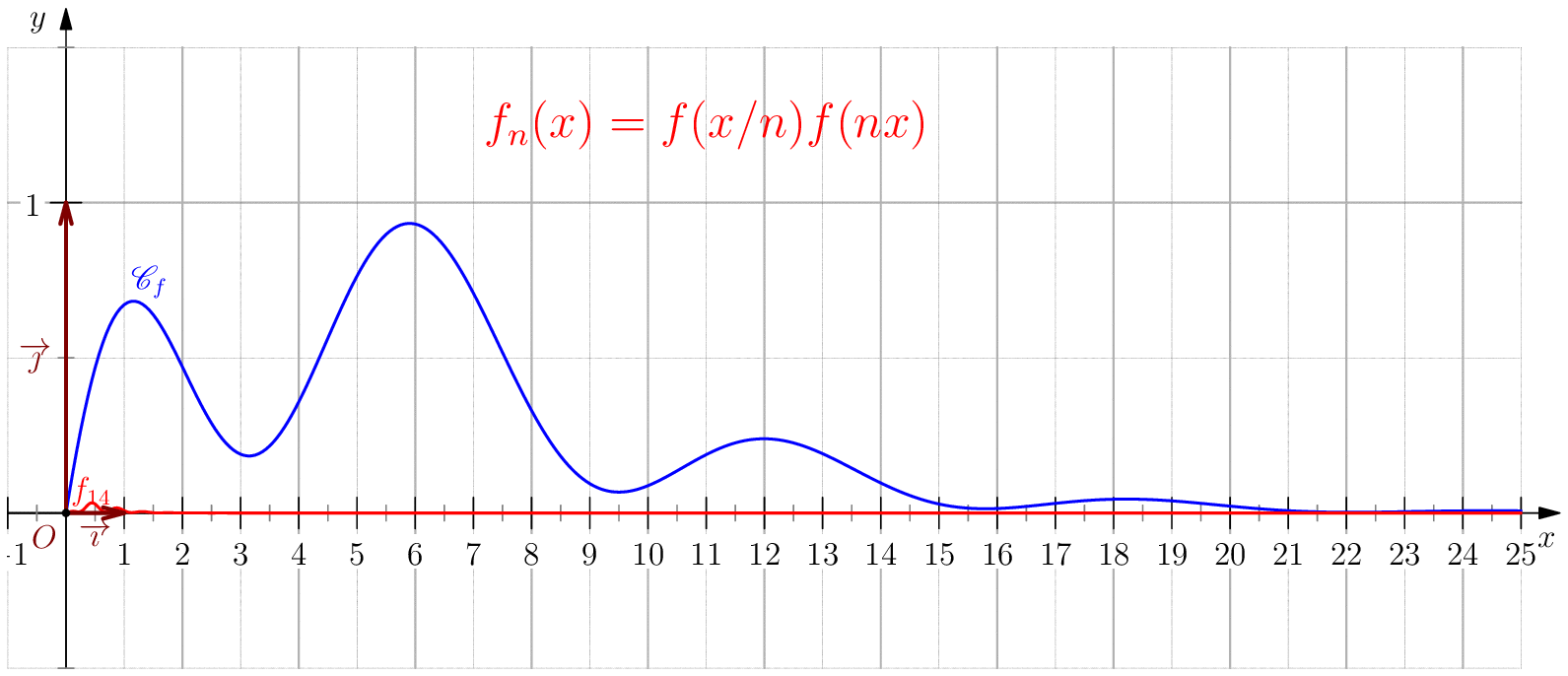
Soit $f$ une application de $\R_+$ dans $\R$ telle que : $f(0)=0 \ , \ \dsp \lim_{x \rightarrow +\infty}{f(x)} = 0 \ $ et $f$ continue sur $\R_+$. Étudier chacune des suites de fonctions définies sur $\R_+$ par : $$\mathbf{a)\,}\,f_n(x) = f(nx);\,\mathbf{b)\,}\,f_n(x)=\dfrac{f(nx)}{n};\,\mathbf{c)\,}\,f_n(x) = f \left(\dfrac{x}{n}\right);\,\mathbf{d)\,}\,~f_n(x) = \dfrac{1}{n}f\left(\dfrac{x}{n}\right);$$ et enfin $\,\mathbf{e)\,}\,~f_n(x)=f(nx)f\left(\dfrac{x}{n}\right).$
Traduisons les données de $f$. $$\forall \varepsilon>0,\,\exists\eta >0,\forall x\leq \eta,~~\abs{f(x)}\leq \varepsilon,\quad \exists A>0,~~\forall x\geq A,\,\,\abs{f(x)}\leq \varepsilon.$$ Notons également que dans ce cas $f$ est bornée, de plus il existe $x_1\geq 0$ tel que $\abs{f(x_1)}=\norme{f}_\infty$.
Le cas $f=0$ est trivial, on suppose alors que $f\neq 0$, i.e. il existe $x_0>0$ tel que $f(x_0)\neq 0$.
a) Pour tout $x>0$, on a $nx\tendvers{n}{\infty}\infty$, donc $f(nx)\tendvers{n}{\infty}0
$ (car $f$ est continue),
d'autre part comme $f_n(0)=f(0)=0$, on en déduit $\boxed{f_n\overset{C.S}{\longrightarrow}
0}$.
La convergence n'est pas uniforme sur $\R_+$ puisque $\abs{f_n(x_0/n)}=\abs{f(x_0)}>0$.
Pour tout $b>0$, on a $\boxed{f_n\overset{C.U}{\longrightarrow} 0}$ sur $[b,\infty[$ car pour
$n\geq \dfrac{A}{b}$ on a
$nx\geq nb\geq A$ donc $\abs{f_n(x)}=\abs{f(nx)}\leq \varepsilon$.
b) $\boxed{f_n\overset{C.U}{\longrightarrow} 0}$.
c) Pour tout $x\geq 0$, on a $\frac{x}{n}\tendvers{n}{\infty}0$, donc
$f\left(\frac{x}{n}\right)\tendvers{n}{\infty}0 $
(car $f$ est continue), on en déduit $\boxed{f_n\overset{C.S}{\longrightarrow} 0}$.
La convergence n'est pas uniforme sur $\R_+$
puisque $\abs{f_n(nx_0)}=\abs{f(x_0)}>0$.
Pour tout $b>0$, on a $\boxed{f_n\overset{C.U}{\longrightarrow} 0}$ sur $[0,b]$ car pour $n\geq
\dfrac{b}{\eta}$ on a
$\frac{x}{n}\leq \frac{b}{n}\leq \eta$ donc $\abs{f_n(x)}=\abs{f(x/n)}\leq \varepsilon$.
d) $\boxed{f_n\overset{C.U}{\longrightarrow} 0}$.
e) Soit $N\in \N$ tel que $N>\dfrac{A}{\eta}$, alors pour tout $n\geq N$, on a:
$\,--\,$ Pour tout $x\in [\eta,\infty[$, on a $nx\geq n\eta\geq \dfrac{A}{\eta}\eta$, donc
$\abs{f(x/n)f(nx)}\leq \norme{f}_\infty \varepsilon$.
$\,--\,$ Pour $x\in [0,\eta[$, on a $\dfrac{x}{n}\leq x\leq \eta$ donc
$\abs{f(x/n)f(nx)}\leq \norme{f}_\infty \varepsilon$.
Dans tous les cas, on a $\abs{f(x/n)f(nx)}\leq \norme{f}_\infty \varepsilon$ soit
$\boxed{f_n\overset{C.U}{\longrightarrow} 0}$ .
Limites et continuité
Supposons que les éléments de la suites $f_n$ vérifient une propriété $P$ en $a\in \overline{I}$
(limite, continuité, dérivabilité,...), il est normal de se poser la question si la fonction $f$
(limite de la suite $f_n$) vérifie la même propriété $P$ en $a$.
Regardons l'exemple suivant:
Pour $n\in \N^*$, on pose $f_n(x)=\Arctan\left(\frac{x}{n}\right)$. Il est facile de vérifier que $f_n$ converge simplement sur $\R$ vers la fonction $f=0$. Donc $\dsp\lim_{x\to \infty} (\lim_{n\to \infty} f_n(x))=0$, d'autre part, pour tout $n\in \N^*$, on a $\dsp\lim_{x\to \infty} f_n(x)=\dfrac{\pi}{2}$. Donc la fonction limite $f$ ne vérifie pas la même propriétés que les fonctions $f_n$.
Ce théorème peut parfois servir à montrer qu'il
Intégration d'une suite de fonctions
Les deux hypothèses « convergence uniforme » et « l'intervalle d'intégration est un segment » sont indispensables, comme le montrent les exemples suivants:
- Soit $(f_n)_{n\geq 1}$ la suite de fonctions définies sur $[0,1]$ par $f_n(x)=n^2x^n(1-x)$. On vérifie alors que la suite $(f_n)$ converge simplement sur $[0,1]$ vers la fonction nulle. Cependant, pour tout $n\in \N^*$, $$\dsp\int_0^1f_n(t)\ud t =\dfrac{n^2}{(n+1)(n+2)}\tendversN\,1\neq 0=\int_0^10\ud t.$$
- Soit $(f_n)_{n\geq 2}$ la suite de fonctions définies par $$f_n(t)=\dfrac1n \,\, \forall t\in \left[0,n-\frac1n\right]\,;\,\, f_n(t)=0 \quad\text{pour }t\geq n\quad et\,\, f_n \text{ continue affine par morceaux.}$$ Alors $\norme{f_n}_\infty^{\R_+}=\dfrac1n$ donc la suite $(f_n)$ converge uniformément sur $\R_+$ vers la fonction nulle. Cependant, on vérifie facilement que $\dsp\lim_{n\to +\infty}\dsp\int_{\R_+}f_n =1$.
Dérivation d'une suite de fonctions
Soit $(f_n)$ une suite de fonctions de classe $\CC^1$, convergeant simplement sur un intervalle $I$ vers une fonction $f$ de classe $\CC^1$.
On peut alors se poser la(es) question(s):
- $\mathbf{1)}\,$ La suite $(f_n')$ converge simplement sur $I$?
- $\mathbf{2)}\,$ Si oui, y-t-il un lien entre $\dsp\lim f_n$ et $f'$.
Même si (intuitivement) on a envie de répondre oui à ces questions, mais en générale, on n'a pas nécessairement la convergence de $f_n')$ et même en cas de convergence on n'a pas forcement $(\dsp\lim f_n)'=\dsp\lim f'_n$, même s'il y a convergence uniforme!
- Soit $f_n :x\in \R \mapsto \dfrac{\sin nx}{ \sqrt n}$ pour $n\in \N^*$. Alors $\norme{f_n}_\infty=\dfrac1{\sqrt n}$, donc la suite $(f_n)$ converge uniformément sur $\R$ vers la fonction nulle. Cependant, $f'_n(x)=\sqrt{n}\cos nx$, et la suite $(f'_n)$ n'a même pas de limite simple!
- Soit $f_n :x\in [-1,1]\mapsto \sqrt{x^2+\dfrac{1}{n}}$ pour $n\in \N^*$. La suite $(f_n)$ converge uniformément sur $\R$ vers la fonction $x\mapsto \abs{x}$. On a $f_n\in \CC^1$ mais la limite n'est pas une fonction de classe $\CC^1$.
- La suite de fonctions $(f_n)$ converge simplement sur $I$ vers une fonction $f$.
- La suite de fonctions $(f'_n)$ converge simplement sur $I$ vers une fonction $g$, la convergence étant uniforme sur tout segment inclus dans $I$.
Alors, la fonction $f$ est de classe $\CC^1$ sur $I$, la suite $(f_n)$ converge uniformément vers $f$ sur tout segment inclus dans $I$, et, pour tout $x\in I$, $f'(x)=g(x)$ (soit, en abrégé, $(\dsp\lim f_n)'=\dsp\lim f'_n$).
- Pour tout $0\leq j\leq k-1$, la suite de fonctions $(f_n^{(j)})$ converge simplement sur $I$.
- La suite de fonctions $(f^{(k)}_n)$ converge simplement sur $I$ vers une fonction $g$, la convergence étant uniforme sur tout segment inclus dans $I$.
Alors, la fonction $f=\dsp\limiteX{n}{\infty}f_n$ est de classe $\CC^k$ sur $I$, et pour chaque $0\leq j\leq k$ la suite $(f_n^{(j)})$ converge uniformément sur tout segment inclus dans $I$, et, pour tout $x\in I$, $f^{(k)}(x)=g(x)$.
- Pour tout $j\in \N$, la suite de fonctions $(f_n^{(j)})$ converge simplement sur $I$.
- Il existe $p\in \N^*$ tel que, pour tout $k\geq p$ la suite de fonctions $(f^{(k)}_n)$ converge simplement sur $I$ vers une fonction $g$, la convergence étant uniforme sur tout segment inclus dans $I$.
Alors, la fonction $f=\dsp\limiteX{n}{\infty}f_n$ est de classe $\CC^\infty$ sur $I$, et pour chaque $j\in \N$ la suite $(f_n^{(j)})$ converge uniformément sur tout segment inclus dans $I$ vers $f^{(j)}$.
Séries de fonctions
Weierstrass en 1872
donne un exemple d'une fonction continue
nulle par dérivable en utilisant les séries des fonctions.
Utilisation des séries de fonctions dans
l'analyse de
Fourier.
Exemple d'une série de Fourier
Généralités
Avant de commencer à étudier la convergence uniforme, on commence par trouver $x\in \R$ tel que
$\dsum u_n(x)$ (donc il s'agit ici d'une
(A Eviter)
Surtout, il faut éviter les phrases de type:
Pour tout $n\in \N$, $u_n$ est définie sur $\R$ donc $\dsum u_n$ est définie sur $\R$.
Exemple d'une réponse à éviter!
Deuxième exemple
(Mines 2018)
Le jury rappelle qu'il faut préciser sur quel ensemble a lieu telle ou telle convergence.
Dans la manipulation des séries de fonctions (recherche d'équivalent d'une somme, estimation du
reste,
...) de nombreux candidats commettent des confusions entre la variable utilisée et l'indice de
sommation.
(CCP 2016)
On note beaucoup de confusions entre suites et séries de fonctions lors, par exemple, de
l'étude d'une convergence uniforme.
Soit $\alpha\in \R^*$ fixé. Pour tout $n\in \N$, $x\in \R$, on définit $u_n(x)=\dfrac{\alpha^n\cos(nx)}{n!}$.
- Déterminer l'ensemble de définition $\DD$ de la fonction $C=\dsum u_n$, puis étudier la convergence uniforme de $\dsum u_n$ sur $\DD$.
- Pour tout $x\in \DD$, donner une expression de $C(x)$ à l'aide des fonctions usuelles.
- Soit $x\in \R$, on a $\abs{u_n(x)}=\dfrac{\abs{\alpha}^n\abs{\cos(nx)}}{n!}\leq \dfrac{\abs{\alpha}^n}{n!}$, or la série $\dsum \dfrac{\abs{\alpha}^n}{n!}$ est une série convergente, on en déduit que $\dsum u_n(x)$ est absolument convergente donc convergent. Donc le domaine de définition $\DD$ de la fonction $C$ est $\R$. D'autre part, pour tout $n\in \N$, $$\abs{R_n(x)}=\abs{\dsum_{k=n+1}^\infty\dfrac{\alpha^k\cos(kx)}{k!}}\leq \dsum_{k\geq n+1}\dfrac{\abs{\alpha}^k\abs{\cos(kx)}}{k!}\leq \dsum_{k\geq n+1}\dfrac{\abs{\alpha}^k}{k!}$$ Ce qui implique $\norme{R_n}_\infty\leq \dsum_{k\geq n+1}\dfrac{\abs{\alpha}^k}{k!} \tendversN\,0$, donc $R_n$ converge uniformément vers $0$ sur $\R$. Donc $\dsum u_n$ converge uniformément vers $C$ sur $\R$.
- Soit $x\in \R$, on a $$C(x)=\dsum_{n=0}^\infty\dfrac{\alpha^n\cos(nx)}{n!}=\re\left(\dsum_{n=0}^\infty\dfrac{\alpha^n\ee^{\ii x}}{n!}\right)=\re \left(\dsum_{n=0}^\infty\dfrac{(\alpha\ee^{\ii x})^n}{n!}\right)=\re\left(\ee^{\alpha\ee^{\ii x}}\right).$$ or, $\dsp \ee^{\alpha\ee^{\ii x}}= \ee^{\alpha(\cos(x)+\ii\sin(x))}=\ee^{\alpha\cos(x)}\ee^{\ii \alpha \sin(x)}$, d'où $$\boxed{\forall x\in \R,\,C(x)=\ee^{\alpha\cos(x)}\cos\left(\alpha\sin(x)\right)}.$$
Étude de la série de fonctions $\dsum_{n\geq 1}\dfrac{x^n}{n^2}$.
-
Convergence simple:
Pour $\abs{x}>1$, $\dfrac{x^n}{n^2}$ ne tend pas vers $0$ quand $n\to+\infty$, donc la
série
$\dsum_{n\geq 1}\dfrac{x^n}{n^2}$ diverge grossièrement.
Si $\abs{x}\leq 1$, $\abs{\dfrac{x^n}{n^2}}\leq \dfrac1{n^2}$ donc la série $\dsum_{n\geq 1} \dfrac{x^n}{n^2}$ est absolument convergente (donc convergente) par comparaison à la série convergente à termes positifs $\dsum_{n\geq 1}\dfrac1{n^2}$.
En conclusion, la série converge simplement sur $[-1,1]$ et on peut donc poser: $$\forall x\in [-1,1]\ ,\ f(x)=\dsum_{n=1}^{+\infty}\dfrac{x^n}{n^2}\,.$$ - Convergence uniforme: Pour tout $x\in [-1,1]$, on a $$\abs{R_n(x)}=\abs{\dsum_{k=n+1}^{+\infty}\dfrac{x^k}{k^2}}\leq \dsum_{k=n+1}^{+\infty} \dfrac{\abs{x}^k}{k^2}\leq \dsum_{k=n+1}^{+\infty}\dfrac{1}{k^2}$$ donc $\norme{R_n}_\infty\leq \dsp\sum_{k=n+1}^{+\infty}\dfrac{1}{k^2}$ et $\dsp\lim_{n\to+\infty}\norme{R_n}_\infty=0$ puisque $\dsum_{k=n+1}^{+\infty}\dfrac{1}{k^2}$ est le reste d'une série numérique convergente.
En conclusion, la série de fonctions $\dsum_{n\geq 1}\dfrac{x^n}{n^2}$ converge uniformément vers $f$ sur $[-1,1]$.
(CCP 2018)
La convergence uniforme est très mal comprise et dans le cas des séries de fonctions, même si
certains
candidats pensent à utiliser la suite des restes, ils ne la majorent pas uniformément.
Dans certains cas (en utilisant comparaison série intégrale ou les séries alternées voir E3A2020 ci-après) on peut étudier la suite des restes, mais dans la major partie des cas, il n'est pas facile de montrer la convergence uniforme du reste vers $0$.
On introduit alors un nouveau type de convergence, plus fort que la convergence normale, la convergence normale.
- les fonctions $u_n\in \Bb(I,\K)$ (au moins à partir d'un certain rang)
- et la série numérique $\dsum_{n\geq 0}\norme{u_n}_\infty$ est convergente
L'intérêt de la CN est qu'elle plus simple à montrer (en générale), en effet il suffit de
calculer la norme infinie de $u_n$ ou de majorer $\abs{u_n(x)}$ par une
- La série de fonctions $\dsum_{n\in \N}u_n$ est uniformément convergente sur $I$.
- Pour tout $x\in I$, la série $\dsum_{n\in \N}u_n(x)$ est absolument convergente dans $\K$.
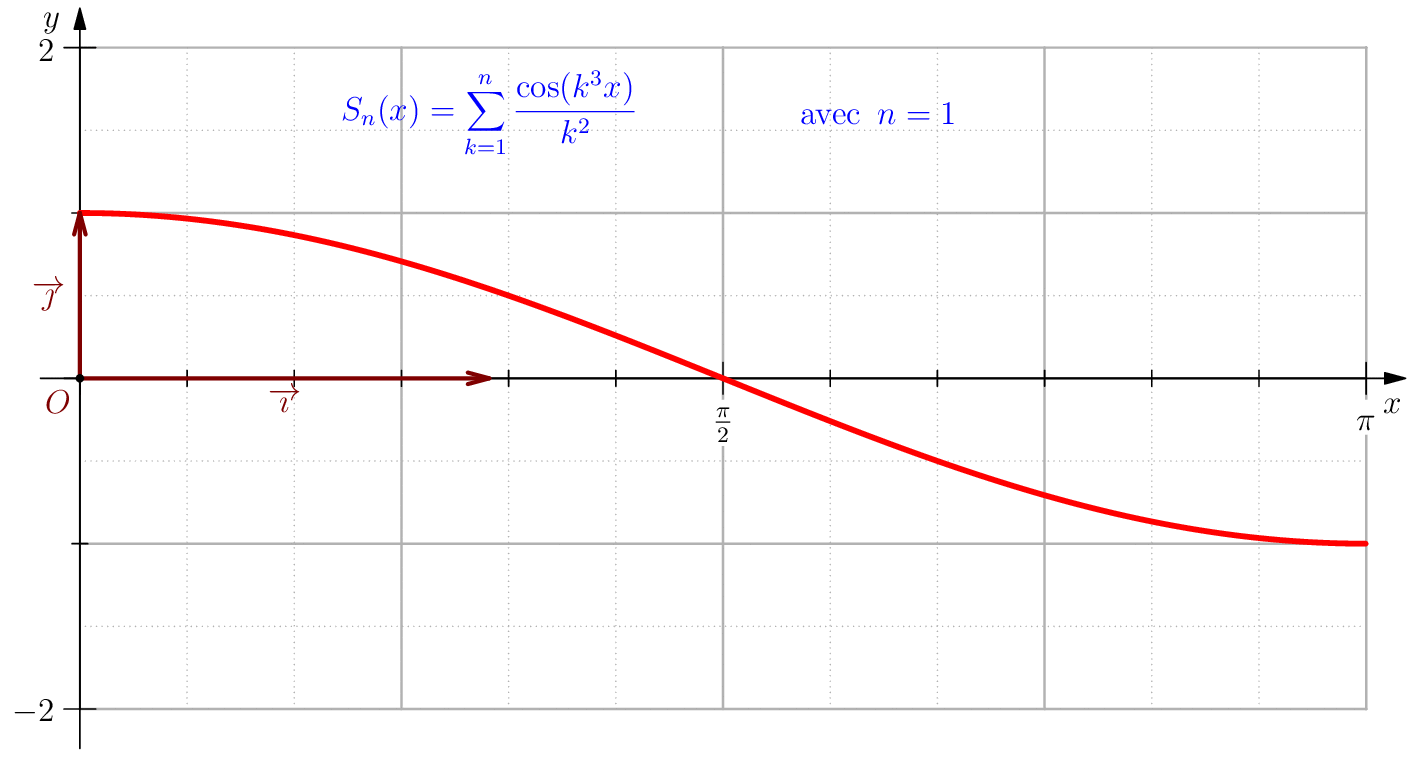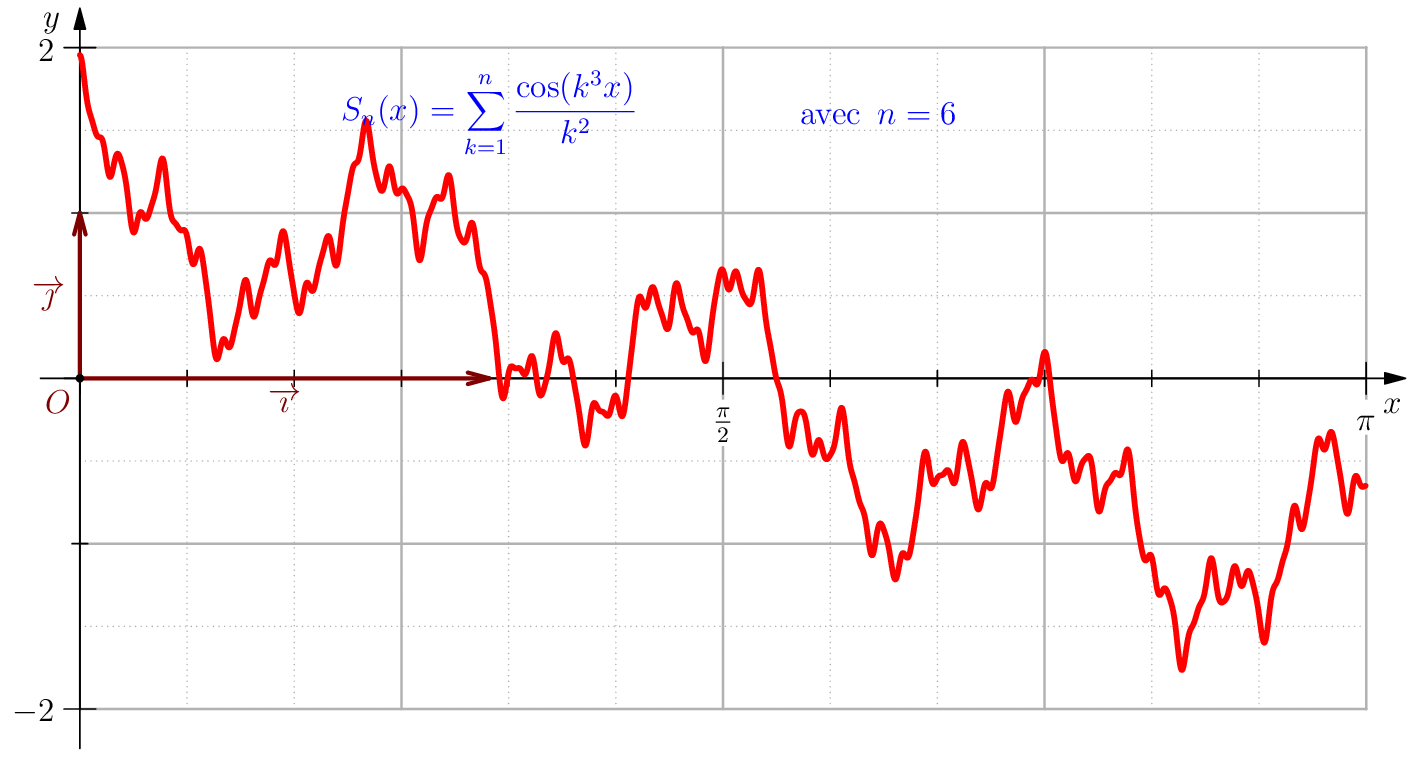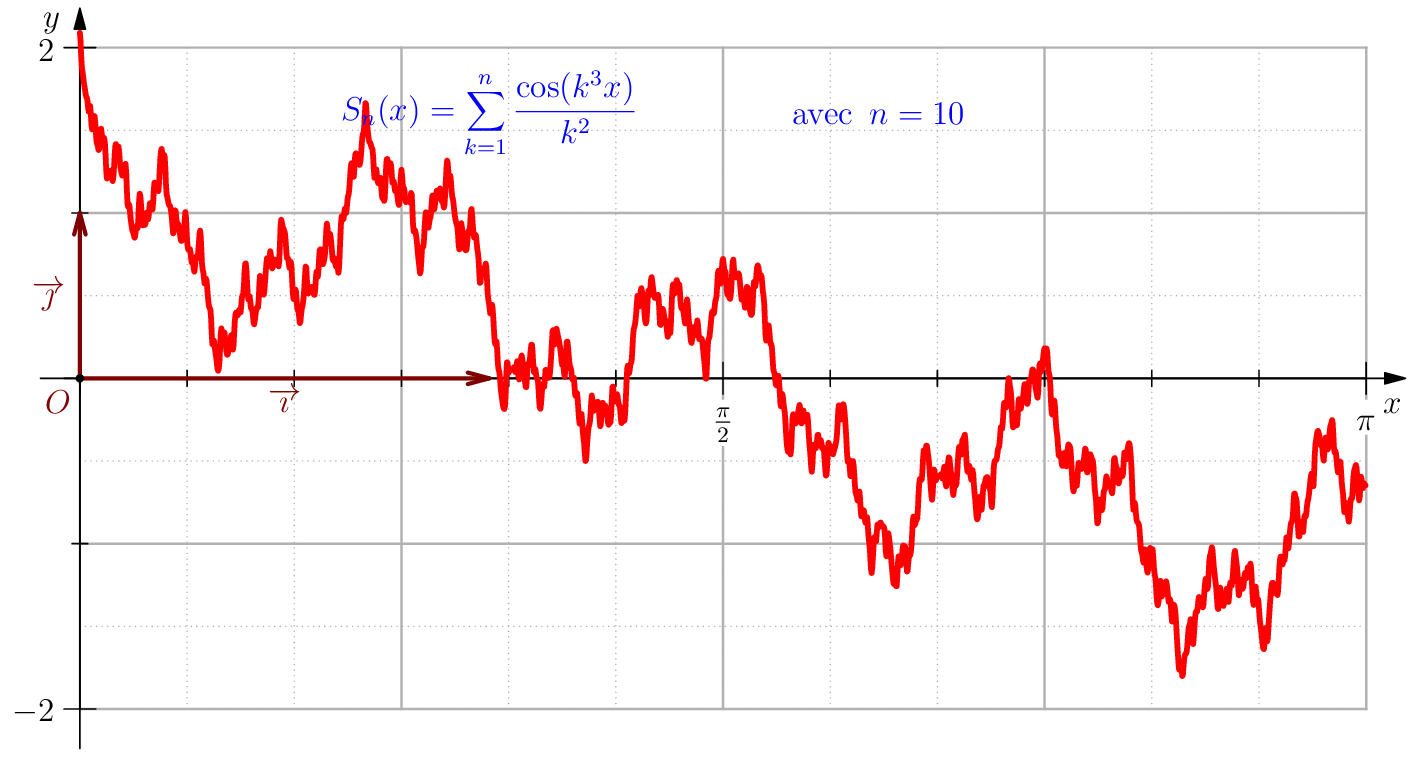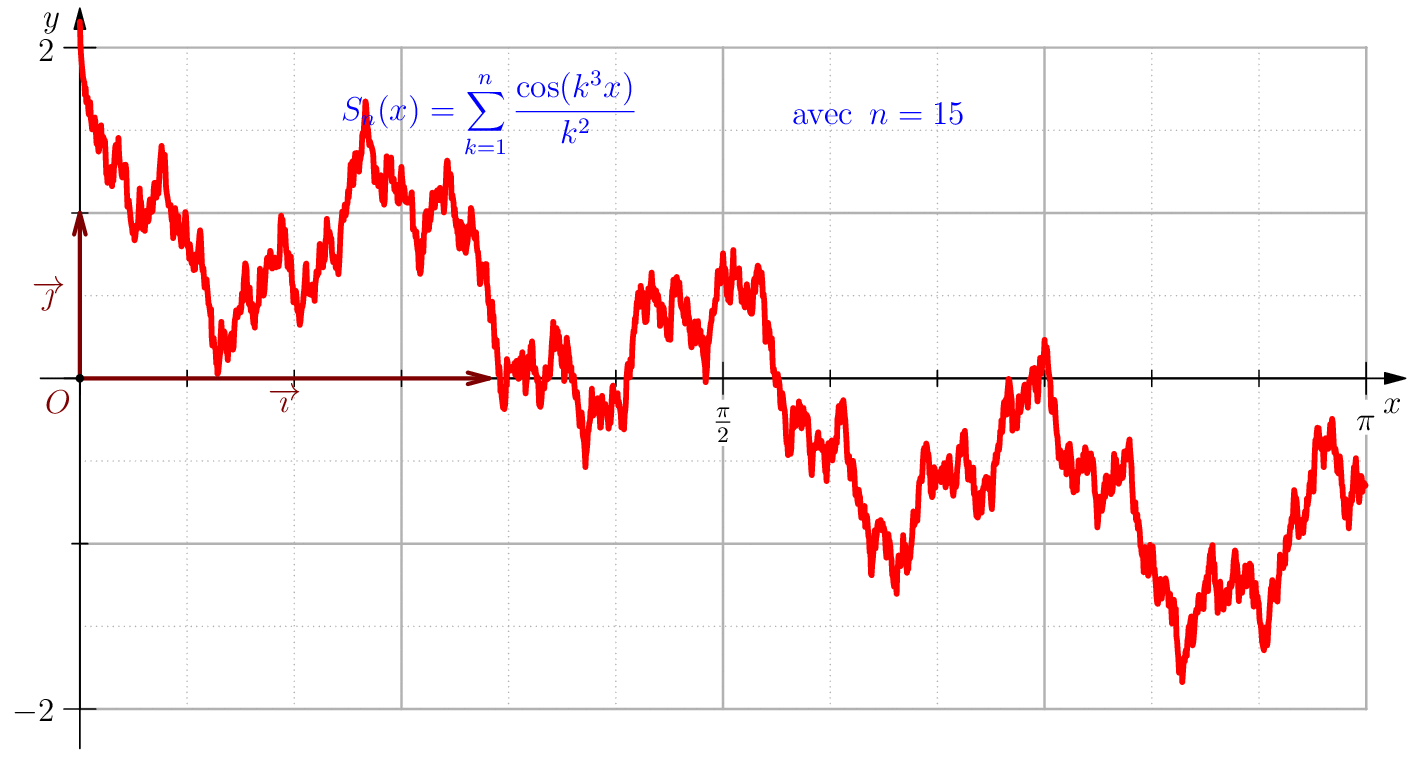
Étude$\dsum_{n\geq 1}\dfrac{\cos(n^3x)}{n^2}$. Dans ce cas, il est facile de majorer $\norme{u_n}_\infty$ par $\dfrac{1}{n^2}$ et comme $\dsum \frac{1}{n^2}$ CV on en déduit que $\dsum u_n $ CN sur $\R$ ce qui évidement implique les autres types de convergence.
Pour $x\in [1,\infty[$, on pose $f_n(x)=\dfrac{(-1)^n}{\sqrt{1+nx}}$. Étudier la convergence de $\dsum f_n$.
Soit $x\geq 1$, la suite $(\dfrac{1}{\sqrt{1+nx}})$ est décroissante et converge vers $0$,
donc d'après le CSSA (c.f. section séries alternées, chapitre
Séries numériques), $\dsum f_n(x)$ converge.
On en déduit que $\dsum f_n $ converge simplement sur $[1,\infty[$. D'autre part, pour tout
$n\geq 0$,
$\norme{f_n}_\infty^{[1,\infty[}=\dfrac{1}{\sqrt{1+n}}$, comme la série $\dsum
\dfrac{1}{\sqrt{1+n}}$ diverge, on en déduit qu'il n'y a pas de convergence normale sur
$[1,\infty[$.
En utilisant le théorème de majoration du reste pour une série alternée (chapitre séries numériques), Soit $x\in [1,\infty[$
$$\abs{R_n(x)}=\abs{\dsum_{k\geq n+1}\dfrac{(-1)^k}{\sqrt{1+kx}}}\leq
\dfrac{1}{\sqrt{1+(n+1)x}}\leq \dfrac{1}{\sqrt{2+n}}\Longrightarrow \norme{R_n}_\infty\leq
\dfrac{1}{\sqrt{2+n}}\tendversN\,0$$
On en déduit alors que $\dsum f_n$ converge uniformément sur $[1,\infty[$.
(E3A 2020)
Il s'agit d'un exercice d'analyse classique sur les différents types de convergence d'une suite (série) de fonctions.
Les notions de convergence normales et uniformes semblent dépasser nombre de candidats. La convergence normale est souvent
assimilée à la convergence absolue. La majoration du reste d'une série alternée même si elle semble connue de la plupart
des candidats, n'est pas toujours appliquée et utilisée correctement.
Certains justifient la divergence d'une série après majoration de son terme général par le terme général d'une série divergente.
On constate une grande confusion chez beaucoup de candidats entre fonction et nombre, entre série numérique et série de
fonctions.
Enfin, il est fréquent de voir les étudiants additionner des équivalents au lieu d'utiliser les développements limités et des o.
Propriétés de la somme d'une série de fonctions
On s'intéresse dans cette section aux propriétés de $\dsum f_n$, par rapport aux propriétés des fonctions $f_n$. Il s'agit essentiellement de la continuité, dérivabilité, intégrabilité de la somme.
Bien évidement, on aura les même problèmes et difficultés que dans le cas des suites de fonctions. Commençons par un exemple.
Soit $F$ une fonction continue définie sur $\R_+$ dans $\R$, on suppose que $F$ admet une limite finie $\ell$ non nul en $\infty$. Pour $n\in \N$, on définie $f_n$ par $$ \fonct{f_n}{\R_+}{\R}{x}{\left\{\begin{array}{ll} (x-n+1)F(x)&\text{ si } n>1 \text{ et } x\in [n-1,n[\\ (n+1-x)F(x)&\text{ si } x\in [n,n+1[\\ 0&\text{ si }x\not\in [n-1,n+1] \end{array}\right. }$$ On note $S_n=\dsum_{k=0}^nf_n$.
- Montrer que $f_n\in \CC(\R_+)$.
- Montrer que $\dsum f_n$ converge simplement vers $F$ sur $\R_+$.
- Calculer $\dsp \lim_{x\to \infty}f_n(x)$ en déduire $\dsp \dsum_{n\geq 0}\lim_{x\to \infty}f_n(x)$. A-t-on $\dsp \lim_{x\to 0}\dsum_{k=0}^\infty f_n(x)=\dsum_{n\geq \infty}\lim_{x\to \infty}f_n(x)$
- La convergence est-elle uniforme sur $\R_+$?
- La série $\dsum_{n\in \N}\ell_n$ converge
- $\dsp\lim_{\substack{x \to a \\x\in I}}S(x)=\dsum_{n=0}^{+\infty}\ell_n$ (i.e. en abrégé: $\dsp\lim_{a} \left(\dsum_{n=0}^{+\infty}u_n\right)=\dsum_{n=0}^{+\infty}\dsp\lim_{a}u_n$).
Cauchy a affirmé dans ce son cous 1821 que la continuité des $u_n$ suffit pour avoir la continuité de $u$.
On considère la suite de fonction $\fonct{f_n}{[0,\pi/2]}{\R}{x}{x\sin(x)\cos(x)^n}$. Étudier la série $g=\dsum f_n$, $g\in \CC([0,\frac{\pi}{2})$?
Pour $x=0$, on a $f_n(0)=0$ donc $\dsum f_n(0)$ converge et vaut $0$. Soit $x\in ]0,\frac{\pi}{2}]$, et $n\in \N^*$, on a $$\dsum_{k=0}^nf_k(x)=\dsum_{k=0}^nx\sin(x)\cos^k(x)=x\sin(x)\dfrac{1-\cos(x)^{n+1}}{1-\cos(x)}\tendversN\dfrac{x\sin(x)}{1-\cos(x)}.$$ On en déduit que $\dsum f_n\overset{C.U}{\tendversN}f$ avec $f(x)=\left\{\begin{array}{ll} 0&\text{ si }x=0\\ \dfrac{x\sin(x)}{1-\cos(x)} \end{array} \right.$ . La fonction $g$ n'est pas continue en $0$, car, pour $x\in ]0,\frac{\pi}{2}]$, on a $$g(x)=\dfrac{x^2+\mathrm{o}(x^3)}{1-(1-\frac{x^2}{2}+\mathrm{o}(x^2))}=2+\mathrm{o}(x)\tendvers{x}{0^+}2\neq g(0).$$ Donc $\dsum f_n$ ne converge pas uniformément sur $[0,\frac{\pi}{2}]$.
On suppose que
On note, pour $n\geq 1$, $f_n(x)=\dfrac{\cos(n^3x)}{n^2}$, on $\dsum f_n$ converge normalement sur $\R$ puisque $\norme{f_n}_\infty=\dfrac{1}{n^2}$. Les fonctions $f_n$ sont de classe $\CC^\infty$ sur $\R$. Que peut-on dire sur la régularité de leurs somme?
- les $u_n$ sont de classe $\CC^1$ sur $I$;
- la série de fonctions $\dsum_{n\in \N}u_n$ converge simplement sur $I$; on notera $S$ sa somme;
- la série de fonctions $\dsum_{n\in\N}u'_n$ converge uniformément sur tout segment de $I$
Alors:
- La fonction $S$ est de classe $\CC^1$ sur $I$;
- pour tout $x\in I$, on a : $S'(x)=\dsum_{n=0}^{+\infty}u'_n(x)$.
- Déterminer le domaine de définition $\DD$ de la fonction $f$ définie par $f(x)=\dsum_{n\geq 1}\dfrac{\ee^{-x\sqrt{n}}}{\sqrt{n^3}}$.
- Étudier les propriétés de $f$ sur $\DD$ ainsi que la dérivabilité de $f$ en $0$.
- Déterminer un équivalent de $f$ en $\infty$.
- Posons, pour $n\geq 1$, $\fonct{u_n}{\R}{\R}{x}{\dfrac{\ee^{-x\sqrt{n}}}{\sqrt{n^3}}}$. Pour $x< 0$, on a $\dfrac{\ee^{-x\sqrt{n}}}{\sqrt{n^3}}\tendversN\infty$, donc $x\not\in \DD$. Pour $x\geq 0$, on a $0\leq u_n(x)\leq \dfrac{1}{\sqrt{n^3}}$, et comme $\dsum \dfrac{1}{n^{3/2}}$ converge alors $\dsum u_n(x)$ converge donc $x\in \DD$. On en déduit que $\DD=\R_+$. De plus, on a $\norme{u_n}_\infty^{\R_+}=\dfrac{1}{\sqrt{n^3}}$ donc $\dsum u_n$ converge normalement sur $\DD$.
-
- $f$ est continue sur $\DD$ car $\dsum u_n$ converge normalement (donc uniformément) sur $\DD$ et pour tout $n\geq 1$ $u_n$ est continue sur $\DD$.
- Notons que la fonction $x>0\longmapsto \dfrac{f(x)-f(0)}{x}$ est strictement décroissante sur $\R_+^*$ et continue donc elle admet une limite en $0$ (éventuellement $-\infty$). Pour tout $n\geq 1$, on a $u_n\in \CC^1(\DD)$ et $u_n(x)'=\dfrac{-\ee^{-x\sqrt{n}}}{n}$. Soit $a>0$, on a $$\forall x\in [a,\infty[,\quad \abs{u_n'(x)}\leq \dfrac{\ee^{-a\sqrt{n}}}{n} \Longrightarrow\norme{u_n'}_\infty^{[a,\infty[}\leq \dfrac{\ee^{-a\sqrt{n}}}{n}\Longrightarrow \dsum_{n\geq 1}\norme{u_n'}_\infty^{[a,\infty[}< \infty.$$ Ceci prouve que $\dsum u_n'$ converge normalement (donc uniformément) sur $[a,\infty[$, d'où $\dsum u_n'$ converge uniformément localement sur $\R_+^*$. On en déduit que $f\in \CC^1(\R_+^*)$.
- Pour $N\in \N$ et $x>0$, on pose $g_N(x)=\dsum_{n=1}^N\dfrac{\ee^{-x\sqrt{n}}-1}{x\sqrt{n^3}}=\dsum_{n=1}^N\dfrac{1}{n}\left(\dfrac{\ee^{-x\sqrt{n}}-1}{x\sqrt{n}}\right)$. La fonction $\varphi(t)=\dfrac{\ee^{-t}-1}{t}$ est continue sur $\R^*$ et prolongeable par continué en $0$ en posant $\varphi(0)=-1$. On en déduit que $g_N$ est prolongeable par continuité en $0$ avec $$g_N(0)=\limiteX{x}{0^+}\dsum_{n=1}^N\dfrac{1}{n}\left(\dfrac{\ee^{-x\sqrt{n}}-1}{x\sqrt{n}}\right)=\dsum_{n=1}^N\limiteX{x}{0^+}\varphi(x\sqrt{n})\dfrac{1}{n}=-\dsum_{n=1}^N\dfrac{1}{n}$$ Soit $x>0$, on a $$\dfrac{f(x)-f(0)}{x}=\dsum_{n\geq 1}\dfrac{\ee^{-x\sqrt{n}}-1}{x\sqrt{n}}\dfrac{1}{n}\leq g_N(x)\Longrightarrow\limiteX{x}{0^+}\dfrac{f(x)-f(0)}{x}\leq \limiteX{x}{0^+}g_N(x)=-\dsum_{k=1}^N\dfrac{1}{k}$$ Ceci étant vrai pour tout $N\in \N^*$, on en déduit alors que $\dsp\limiteX{x}{0^+}\dfrac{f(x)-f(0)}{x}=-\infty$ puisque $\dsum\dfrac{1}{k}$ diverge. On conclut que $f$ n'est pas dérivable en $0$.
- $\dsum u_n$ CU sur $[1,\infty[$, de plus, pour tout $n\geq 1$, on a $u_n(x)\tendvers{x}{\infty}0$, on en déduit: $$\limiteX{x}{\infty}f(x)=\dsum_{n\geq 1}\limiteX{x}{\infty}u_n(x)=0.$$ Pour trouver un équivalent de $f$ en $\infty$, on écrit, $$\begin{array}{lcl} f(x)&=&\ee^{-x}+\dfrac{\ee^{-x\sqrt{2}}}{2}+\dfrac{\ee^{-x\sqrt{3}}}{3}+\cdots =\ee^{-x}\left(1+\dfrac{\ee^{-x(\sqrt{2}-1)}}{2}+\dfrac{\ee^{-x(\sqrt{3}-1)}}{3}+\cdots\right)\\ &&\\ &=&\ee^{-x}\left(1+\dsum_{k\geq 2}\dfrac{\ee^{-x(\sqrt{k}-1)}}{k}\right)=\ee^{-x}\left(1+h(x)\right) \end{array} $$ ensuite on montre que $h(x)\tendvers{x}{\infty}0$, ce qui donne $f(x)\underset{x\to \infty}{\thicksim} \ee^{-x}$.
- les $u_n$ sont de classe $\CC^k$ sur $I$;
- chaque série de fonctions $\dsum_{n\in \N}u_n^{(j)}$, $0\leq j\leq k-1$, converge simplement sur $I$;
- la série de fonctions $\dsum_{n\in\N}u_n^{(k)}$ converge uniformément sur tout segment inclus dans $I$.
Alors:
- La fonction $S=\dsum u_n$ est de classe $\CC^k$ sur $I$;
- chaque série $\dsum u_n^{(j)},\,0\leq j\leq k$, converge uniformément sur tout segment de $I$ avec pour fonction somme $S^{(j)}$ $$\forall 0\leq j\leq k,\quad \forall x\in I,\quad S^{(j)}(x)=\dsum_{n\geq 0}u_n^{(j)}(x).$$
- les $u_n$ sont de classe $\CC^\infty$ sur $I$;
- chaque série de fonctions $\dsum_{n\in \N}u_n^{(j)}$, $j\in \N$, converge simplement sur $I$;
- il existe $p\in \N^*$ tel que, pour tout $k\geq p$, la série de fonctions $\dsum_{n\in\N}u_n^{(k)}$ converge uniformément sur tout segment inclus dans $I$.
Alors:
- La fonction $S=\dsum u_n$ est de classe $\CC^\infty$ sur $I$;
- chaque série $\dsum u_n^{(j)},j\in \N$, converge uniformément sur tout segment de $I$ avec pour fonction somme $S^{(j)}$ $$\forall j\in \N,\quad \forall x\in I,\quad S^{(j)}(x)=\dsum_{n\geq 0}u_n^{(j)}(x).$$
- Déterminer le domaine de définition $\DD$ de la fonction $f$ définie par $f(x)=\dsum_{n\geq 2}\dfrac{n^{-x}}{\ln(n)}$.
- Montrer que $f$ est de classe $\CC^\infty$ sur $\DD$.
- Déterminer une équivalent de $f$ en $\infty$.
-
Poux $x\leq 1$ et $n\geq 2$, on a $\dfrac{n^{-x}}{\ln(n)}\geq \dfrac{1}{n\ln(n)}$ et
$\dsum \dfrac{1}{n\ln(n)}$ diverge donc $x\not\in \DD$.
Pour $x>1$ on a
$\dfrac{n^{-x}}{\ln(n)}=\underset{n\to \infty}{\mathrm{o}}
\left(\dfrac{1}{n^{\frac{1+x}{2}}}\right)$ et $\dsum \dfrac{1}{n^{(1+x)/2}}$ converge
donc $x\in \DD$.
On en déduit $\boxed{\DD=]1,\infty[}$. - Posons, pour $n\geq 2$, $\fonct{f_n}{]1,\infty[}{\R}{x}{\dfrac{1}{n^x\ln(n)}}$, on a $f_n\in \CC^\infty(]1,\infty[)$. De plus, $$\forall p\in \N^*,\, \forall x\in ]1,\infty[,\, f_n^{(p)}(x)=\dfrac{\ln(n)^{p-1}}{n^x}\Longrightarrow \forall a>1,\, \norme{f_n^{(p)}}_\infty^{[a,\infty[}\leq \dfrac{\ln(n)^{p-1}}{n^a},$$ on en déduit alors que $\dsum_{n\geq 2} \norme{f_n^{(p)}}_\infty^{[a,\infty[}<\infty$. Donc la série $\dsum f_n^{(p)}$ converge normalement sur tout intervalle de type $[a,\infty[$ pour tout $a>1$. On en déduit que $\dsum f_n^{(p)}$ converge uniformément localement sur $]1,\infty[$. Le résultat étant vérifié pour tout $p\in \N$, on en déduit alors que $f\in \CC^\infty(]1,\infty[)$.
- Pour tout $n\geq 2$, on a $f_n(x)=\dfrac{1}{n^x\ln(n)}\tendvers{x}{\infty}0$. Comme $\dsum f_n$ converge normalement sur $[a,\infty[$ ($a>1$), on en déduit alors que $\dsp\limiteX{x}{\infty}f(x)=\dsum_{n\geq 2}\limiteX{x}{\infty}f_n(x)=0$. D'autre part, on a $$\begin{array}{lcl} f(x)&=&\dfrac{1}{2^x\ln(2)}+\dfrac{1}{3^x\ln(3)}+\cdots +\dfrac{1}{n^x\ln(n)}+\cdots\\ & =&\dfrac{1}{2^x\ln(2)}\left(1+\left(\frac{2}{3}\right)^x\frac{\ln(2)}{\ln(3)}+\cdots +\left(\frac{2}{n}\right)^x\frac{\ln(2)}{\ln(n)}+\cdots\right) \end{array} $$ Ainsi, $\dsp\ln(2)2^xf(x)=1+\dsum_{n\geq 3}\left(\dfrac{2}{n}\right)^x\dfrac{\ln(2)}{\ln(n)}\tendvers{x}{\infty}1$. On en déduit, $\boxed{f(x)\underset{x\to\infty}{\thicksim}\dfrac{1}{2^x\ln(2)}}$.