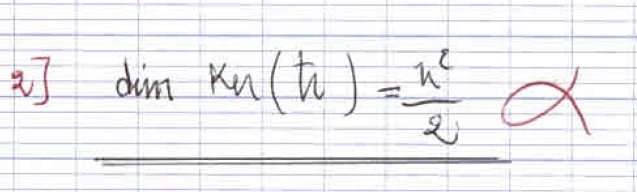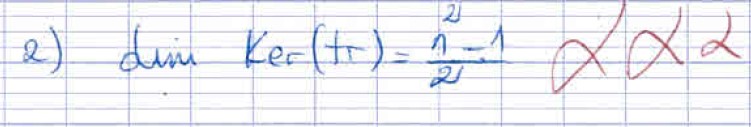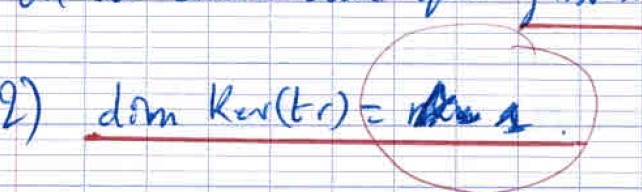Matrices II
Trace d'une matrice, d'un endomorphisme
Trace d'une matrice
-
L'application $\mathrm{tr}$ : $\MM_{n}(\K) \rightarrow \K$ est une
forme linéaire . -
$ \forall A \in \MM_{n,p}(\K)$ et $\forall B \in \MM_{p,n}(\K)$,
$\mathrm{tr} (AB) = \mathrm{tr} (BA)$ .
-
Soient $A,B,C \in \MM_{n}(\K)$. Le résultat ci-dessus donne :
$$ \mathrm{tr} (ABC) = \mathrm{tr}(BCA) = \mathrm{tr}(CAB)$$
mais on n'a pas $\mathrm{tr}(ABC)= \mathrm{tr}(BAC)$ en général.
Exemple: $A=\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} \ , \quad B=\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} \ , \quad C= \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}$. - La démonstration du théorème précédent doit être connue, et peut faire l'objet d'une question du concours, par exemple E3A 2019 (MP). Mais aussi Centrale PSI 2022 et aussi Centrale PSI 2023!!! (c.f. rapport du jury ci-après)
-
L'application $\mathrm{tr}$ est une forme linéaire, donc en utilisant le théorème du
rang, on trouve facilement $\boxed{\dim (\Ker(\mathrm{tr}))=n^2-1}$. Bien que ce
résultat semble évident,
mais pose beaucoup de problème aux élèves,
-
Une réponse extra-terrestre.
-
Une réponse avec justification
-
Une réponse sans justification
-
Une blague belge (en faite 2).
-
Enfin, pour terminer, une réponse sans réponse,
-
Une réponse extra-terrestre.

Rapport du jury -- Centrale 2022
Il était attendu des candidats qu'ils maitrisent bien leur cours d'algèbre linéaire pour traiter ce problème : propriétés de la trace ou du déterminant, manipulations de matrices et de leurs puissances, définition d'une valeur propre par exemple. Une bonne maitrise des raisonnements élémentaires de probabilités était également indispensable : indépendance ou incompatibilité d'évènements, propriétés de l'espérance et de la variance. Enfin, quelques autres chapitres (espaces euclidiens, études de fonctions) rentraient également en jeu.
La première partie a été abordée presque entièrement par tous les candidats, et certaines questions ont été très bien traitées. En revanche, le cours n'est pas toujours bien appris et certains résultats, pourtant très importants, ne sont parfois pas cités correctement (propriétés de la trace ou formule du binôme de Newton par exemple).
Soient $A,B\in \MM_n(\K)$ tel que $\rg(AB-BA)=1$. Calculer $(AB-BA)^2$.
Puisque $\rg(AB-BA)=1$ alors il existe $X\in \MM_{n\,1}(\K),\, Y\in \MM_{1\,n}(\K)$ (voir aussi exo matrices) tels que $$X\neq 0,\, Y\neq 0,\quad AB-BA =X\cdot Y.$$ Ce qui donne, $$(AB-BA)^2 =(X\cdot Y)(X\cdot Y)=X (Y\cdot X) Y = (Y\cdot X) (X\cdot Y)= (Y\cdot X) (AB-BA).$$ mais $Y\cdot X=\dsum_{i=1}^n x_iy_i =\mathrm{tr} (X\cdot Y)=\mathrm{tr} (AB-BA)=0$ puisque $\mathrm{tr}( AB-BA)=\mathrm{tr}(AB)-\mathrm{tr}(BA)$.
On en déduit alors que $(AB-BA)^2=0$.
Trace d'une endomorphisme
Ce scalaire s'appelle la
Montrer que $f$, définie sur $\R_n[x]$ par $f(P)(x)=\dsp\int_x^{x+1}P(t)\ud t$ est un endomorphisme et donner sa trace.
On note $E=\R_n[x]$ et $\BB=(e_0,\cdots,e_n)$ la base canonique de $E$ (avec $e_i(x)=x^i$).
Soient $P_1,\,P_2\in E$ et $\lambda\in \R$, on note $Q=\varphi(\lambda P_1+P_2)$. Alors,
$$
\begin{array}{lcl}
\forall x\in \R,\,Q(x)&=& \dsp\int_x^{x+1}(\lambda P_1+P_2)(t)\ud t=\int_x^{x+1}(\lambda
P_1(t)+P_2(t))\ud t\\
&&\\
&=&\dsp\lambda\int_x^{x+1}P_1(t)\ud t+\int_x^{x+1}P_2(t)\ud t=\lambda \varphi
(P_1)(x)+\varphi(P_2)(x).
\end{array}
$$
On en déduit alors, $\varphi (\lambda P_1+P_2)=\lambda\varphi(P_1)+\varphi (P_2)$ ce qui montre
que
$\varphi$ est linéaire.
Montrons que $f(E)\subset E$, pour cela il suffit de calculer $f$ de la base canonique.
Soit $k\in \inter{0,n}$, on a
$$
\begin{array}{lcl}
\forall x\in \R,\,f(e_k)(x)&=& \dsp\int_x^{x+1}t^k\ud
t=\dfrac{1}{k+1}\left[t^{k+1}\right]_x^{x+1}
=\dfrac{1}{k+1}\left((x+1)^{k+1}-x^{k+1}\right)\\
&&\\
&=&\dsp \dfrac{1}{k+1}\left(\dsum_{j=0}^{k+1}\binom{k+1}{j}x^j-x^{k+1}\right)\\
&&\\
&=&\dsp\dfrac{1}{k+1}\left(\textcolor{red}{x^{k+1}}+\dsum_{j=0}^{k}\binom{k+1}{j}x^j-\textcolor{red}{x^{k+1}}\right)=\dfrac{1}{k+1}\dsum_{j=0}^{k}\binom{k+1}{j}x^j\in
E
\end{array}
$$
Ceci prouve que $f\in \LL(E)$.
D'autre part, le calcul précédent, montre que, pour tout $k\geq 1$,
$$f(e_k)(x)= \dfrac{1}{k+1}\dsum_{j=0}^{k}\binom{k+1}{j}x^j= \dfrac{1}{k+1}
\left(\binom{k+1}{k}x^k +\dsum_{j=0}^{k-1}\binom{k+1}{j}x^j\right) =x^k +
\dsum_{j=0}^{k-1}\binom{k+1}{j}\dfrac{x^k}{k+1}$$
et on a $f(e_0)=1=e_0$, donc
\begin{equation*}
M(f)_\BB=
\begin{pmatrix}
1 &\frac{1}{2} & \phantom{\cdots} & \phantom{\cdots} &\phantom{\cdots} & & \frac{1}{n+1} \\
0 & 1 & \ddots & & & &\phantom{\vdots} \\
& & \ddots & & &&\vdots \\
& & & &\ddots &&\phantom{\vdots} \\
& & & &\ddots &&\phantom{\vdots}\\
& & & & &1&\frac{1}{2} \\
0 & & &&& 0 & 1
\end{pmatrix}
\Longrightarrow \mathrm{tr}(f)=\mathrm{tr}(M_\BB(f))=n+1.
\end{equation*}
- L'application $\mathrm{tr}$ : $\mathscr{L}(E) \rightarrow \K$ est une forme linéaire.
- $\forall u,v \in \mathscr{L}(E) \ , \ \mathrm{tr}(v \circ u) = \mathrm{tr} (u \circ v)$.
- Si $p$ est un projecteur de $E$, alors : $\mathrm{tr} p= \rg p$.
- Si $E_1$ et $E_2$ sont deux s-e-v supplémentaires de $E$ et si $s$ est la symétrie par rapport à $E_1$ de direction $E_2$, alors: $\mathrm{tr} s= \dim(E_1)-\dim(E_2)$.
Soit $\K$-ev de dimension finie, $f\in \mathrm{GL} (E)$ et $g\in \LL(E)$ tel que $\rg (g)=1$. Montrer l'équivalence, $$f+g\in \mathrm{GL} (E)\Longleftrightarrow \mathrm{tr} (g\circ f^{-1})\neq -1.$$
Puisque $f\mathrm{GL}(E)$ alors on peut écrire $f+g =(\ide +g\circ f^{-1})\circ f$, donc $$f+g\in \mathrm{GL} (E)\Longleftrightarrow \ide +g\circ f^{-1} \in \mathrm{GL} (E).$$ D'autre part, $f^{-1}\in \mathrm{GL} (E)$ donc $\rg(g\circ f^{-1})=\rg (g)=1$, ainsi il existe une base $\BB$ de $E$ tel que $$M_\BB (g\circ f^{-1})=\begin{pmatrix} 0 &0&\cdots &0& a_1\\ \vdots& & &\vdots&a_2\\ \vdots& & &\vdots&\vdots\\ 0 &0&\cdots &0& a_{n-1}\\ 0 &0&\cdots &0& a_n \end{pmatrix}\Longrightarrow M_\BB (\ide +g\circ f^{-1})=\begin{pmatrix} 1 &0&\cdots &0& a_1\\ \vdots&1 & &\vdots&a_2\\ \vdots& & &\vdots&\vdots\\ 0 &0&\cdots &1& a_{n-1}\\ 0 &0&\cdots &0& 1+a_n \end{pmatrix} $$ avec $a_n=\mathrm{tr}(g\circ f^{-1})$. $$f+g\in \mathrm{GL} (E)\Longleftrightarrow \ide +g\circ f^{-1} \in \mathrm{GL} (E)\Longleftrightarrow 1+a_n\neq 0\Longleftrightarrow \mathrm{tr}(g\circ f^{-1})\neq -1 $$
Matrices par blocs
Considérons la matrice $A= \begin{pmatrix} a&b&c&d\\ u&v&w&q\\ x&y&z&r \end{pmatrix}$. On considère $I=\{2,3\},\,J=\{2,3\}$ , on obtient le bloc $$ \begin{pmatrix} \xcancel{a}&\xcancel{b}&\xcancel{c}&\xcancel{d}\\ \xcancel{u}&\textcolor{blue}{v}&\textcolor{blue}{w}&\xcancel{q}\\ \xcancel{x}&\textcolor{blue}{y}&\textcolor{blue}{z}&\xcancel{r} \end{pmatrix} \rightsquigarrow \quad A' =\begin{pmatrix} v&w\\y&z \end{pmatrix} $$
Si on ne suppose plus ces entiers consécutifs, on obtient ce qui est appelé une matrice extraite.
Soit $E$ un $\K$-e-v de dimension finie $n \geqslant1$, $E_1$ et $E_2$ deux s-e-v supplémentaires de $E$, $\textrm{dim}(E_1)=p$, $\dim (E_2)=n-p$, $\mathscr{B}_1$ et $\mathscr{B}_2$ deux bases de $E_1$ et $E_2$ respectivement, et $\mathscr{B} =\mathscr{B}_1 \cup \mathscr{B}_2$, de sorte que $\mathscr{B}$ est une base de $E$.
Soit $u \in \mathscr{L}(E)$, et $A=M_{\mathscr{B}}(u)$, écrite par blocs sous la forme :
$$ \begin{matrix}
&\begin{matrix}
\,\,\underset{\longleftrightarrow}{p}&\underset{\longleftrightarrow}{n-p}
\end{matrix} & \\
\begin{matrix}
\\
A=\\
\\
\end{matrix}&
\begin{bmatrix}
A_1\,\, & B_2 \\
&\\
B_1\,\,& A_2
\end{bmatrix}& \begin{matrix}
\updownarrow \,p\phantom{-n}\\
\\
\updownarrow \,n-p
\end{matrix}
\end{matrix}
$$
On remarquera que $A_1$ et $A_2$ sont des
Alors :
- $E_1$ est stable par $u \, \Longleftrightarrow \, B_1 = 0$.
- $E_2$ est stable par $u \, \Longleftrightarrow \, B_2 = 0$.
-
Ainsi, si $E_1$ est stable par $u$, $A$ est de la forme :
$\begin{bmatrix} A_1 & B_2 \\ 0 & A_2 \end{bmatrix}.$ Une telle matrice est dite
triangulaire supérieure par blocs . $A_1$ est alors la matrice de l'endomorphisme induit par $u$ sur $E_1$. -
Si $E_1$ et $E_2$ sont stables par $u$, $A$ est de la forme
$ \begin{bmatrix} A_1 & 0 \\ 0 & A_2 \end{bmatrix}.$
Une telle matrice est dite
diagonale par blocs . $A_1$ et $A_2$ sont alors les matrices des endomorphismes induits $u|_{E_1}$ et $u|_{E_2}$.
Et, dans ce cas, $A^{-1}$ est de la forme :
$$ \begin{matrix}
&\begin{matrix}
\,\,\underset{\longleftrightarrow}{p}&\underset{\longleftrightarrow}{n-p}
\end{matrix} & \\
\begin{matrix}
\\
A^{-1}=\\
\\
\end{matrix}&
\begin{bmatrix}
A_1^{-1}\,\, & B_2' \\
&\\
0\,\,& A_2^{-2}
\end{bmatrix}& \begin{matrix}
\updownarrow \,p\phantom{-n}\\
\\
\updownarrow \,n-p
\end{matrix}
\end{matrix}
$$
Et, dans ce cas, $A^{-1}$ est de la forme :
$$ \begin{matrix}
&\begin{matrix}
\,\,\underset{\longleftrightarrow}{p}&\underset{\longleftrightarrow}{n-p}
\end{matrix} & \\
\begin{matrix}
\\
A^{-1}=\\
\\
\end{matrix}&
\begin{bmatrix}
A_1^{-1}\,\, & 0 \\
&\\
0\,\,& A_2^{-2}
\end{bmatrix}& \begin{matrix}
\updownarrow \,p\phantom{-n}\\
\\
\updownarrow \,n-p
\end{matrix}
\end{matrix}
$$
Les résultats ci-dessus se généralisent sans difficulté aux cas des matrices triangulaires supérieures par blocs, de la forme : $$\begin{bmatrix} A_{11} & \dots & A_{1n} \cr & \ddots & \vdots \cr {\ \ }^{\dsp \textrm{\huge{0}}} & & A_{nn} \end{bmatrix},$$ où les $A_{ii}$ sont des matrices carrées, et aux matrices diagonales par blocs de la forme $$\begin{bmatrix} A_{11} & & {}_{\dsp \textrm{\huge{0}}} \cr & \ddots & \cr {\ \ }^{\dsp \textrm{\huge{0}}} & & A_{nn} \end{bmatrix}.$$
- Soient $(r,s,t,u)\in \C^4$ et $(e_1,e_2)$ la base canonique de $\C^2$. On note $\varphi$ l'endomorphisme de $\C^2$ dont la matrice dans la base $(e_1,e_2)$ est $\begin{pmatrix} r&s\\t&u \end{pmatrix}$. Exprimer la matrice de $\varphi$ dans la base $(e_2,e_1)$.
- Soit $(R,S,T,U)\in \MM_n(\C)^4$. En s'inspirant de la question précédente, montrer que la matrice $\begin{pmatrix} R&S\\T&U \end{pmatrix}$ est semblable dans $\MM_{2n}(\C)$ à la matrice $\begin{pmatrix} U&T\\ S&R \end{pmatrix} $ . Montrer de même que $\begin{pmatrix} R&S\\T&U \end{pmatrix}$ est semblable à la matrice $\begin{pmatrix} R&-S\\-T&U \end{pmatrix}$ .
- En utilisant la matrice de $\varphi$, on a $$ \left.\begin{array}{l} \varphi(e_2)=se_1+ue_2= ue_2+s e_1\\ \\ \varphi(e_1)=re_1+te_2= te_2+re_1 \end{array}\right\}\Longrightarrow M_{(e_2,e_1)}(\varphi)=\begin{pmatrix} u&t\\ s&r \end{pmatrix}.$$ On aurait aussi pu utiliser la matrice $P$ de passage de $(e_1,e_2)$ à la base $(e_2,e_1)$, i.e. $$M_{(e_2,e_1)}(\varphi) =P^{-1}M_{(e_1,e_2)}(\varphi)P=\begin{pmatrix} 0&1\\ 1&0 \end{pmatrix} \begin{pmatrix} r&s\\t&u \end{pmatrix}\begin{pmatrix} 0&1\\ 1&0 \end{pmatrix} =\begin{pmatrix} u&t\\ s&r \end{pmatrix}. $$
-
Soit $\BB=(e_1,\cdots,e_n,e_{n+1},\cdots,e_{2n})$ la base canonique de $\C^{2n}$. On note $\BB_1=(e_1,\cdots,e_n),\,\BB_2=(e_{n+1},\cdots,e_{2n})$ de sorte que $\BB=(\BB_1,\BB_2)$, on considère $\varphi\in \LL(\C^{2n})$ dont la matrice par blocs dans le base $\BB$ est $\begin{pmatrix}
R&S\\T&U
\end{pmatrix}$, en utilisant la question précédente, on trouve que la matrice de $\varphi$ dans la base $\BB'=(\BB_2,\BB_1)$ est $\begin{pmatrix}
U&T\\
S&R
\end{pmatrix}
$, de même la matrice $\varphi$ dans la base $\BB''=(\BB_1,-\BB_2)$ est $\begin{pmatrix}
R&-S\\-T&U
\end{pmatrix}$.
Ceci prouve que les 3 matrices sont semblables.
Polynômes d'un endomorphisme, polynôme de matrice
Puissances d'un endomorphisme
On définit également la même chose pour une matrice $A\in \MM_n(\K)$.
- la suite $\left(\Ker (u^k)\right)_{k\in \N}$ est croissante i.e. $\Ker(u^k) \subset \Ker(u^{k+1})$.
-
si l'ensemble $\{k \in \N, \ \Ker(u^k) = \Ker(u^{k+1}) \}$ n'est pas vide, il
admet alors un plus petit élément $p$, appelé
indice de $u$ .
Et on a alors : $\begin{cases} \forall k \in \inter{0,p-1}, & \Ker(u^k) \subsetneq \Ker(u^{k+1})\\ \forall k \geqslant p, & \Ker(u^k)= \Ker(u^p) \end{cases}$ - Si $E$ est de dimension finie, alors pour tout endomorphisme $u \in \mathscr{L}(E)$, l'indice $p$ de $u$ existe, et $p \leqslant \dim E$.
- Si $u\in \LL (E)$ est nilpotent, alors l'indice $p$ de $u$ existe. De plus si $\dim (E)< \infty$ alors $p\leq \dim (E)$.
- Soit $u : \ \begin{cases} \K [X] & \rightarrow \K [X] \\ P & \mapsto P' \end{cases}$ . Alors, pour tout $k \in \N^*$, $\Ker(u^k)= \K_{k-1}[X]$, donc l'indice de $u$ n'existe pas.
- Par contre, si l'on considère l'endomorphisme $v : \, \begin{cases} \K_n[X] & \rightarrow \K_n[X] \\ P & \mapsto P' \end{cases}$, alors son indice est égal à $n+1$ (car $v^{n+1}=0 \text{ et } v^n \neq 0$).
- $ \begin{cases} \forall k \in \inter{0,p-1}, & \im (u^{k+1}) \subsetneq \im (u^k) \\ \forall k \geqslant p, & \im (u^{k+1})= \im (u^k) \end{cases} $
- $E = \Ker(u^p) \oplus \im (u^p)$.
L'ensemble $\K[A]$
Soit $A\in \MM_n(\K)$, on définit $B\in \MM_{2n}(\K)$ par $B=\begin{pmatrix} A& 0_n\\ A&A \end{pmatrix}$. Soit $P\in \K[X]$, exprimer $P(B)$ en fonction de $P(A),\, P'(A)$.
Calculons $B^2$, $$B^2=\begin{pmatrix} A& 0_n\\ A&A \end{pmatrix}\begin{pmatrix} A& 0_n\\ A&A \end{pmatrix}=\begin{pmatrix} A^2& 0_n\\ 2A^2&A^2 \end{pmatrix}=\begin{pmatrix} A^2& 0_n\\ A\times (2A)&A^2 \end{pmatrix} .$$ Puis $$B^3=\begin{pmatrix} A^2& 0_n\\ 2A^2&A^2 \end{pmatrix}\begin{pmatrix} A& 0_n\\ A&A \end{pmatrix}=\begin{pmatrix} A^3& 0_n\\ 3A^3&A^3 \end{pmatrix} =\begin{pmatrix} A^3& 0_n\\ A\times (3A^2)&A^3 \end{pmatrix}.$$ On fait alors l'hypothèse: $$\forall k\in \N,\, B^k =\begin{pmatrix} A^k&0_n\\ A\times (kA^{k-1})&A^k \end{pmatrix} $$ La relation est vraie pour $k=1,2,3$. Soit $k\geq 1$ supposons que la relation est vraie au range $k$, alors $$B^{k+1} =BB^k=\begin{pmatrix} A& 0_n\\ A&A \end{pmatrix}\begin{pmatrix} A^k& 0_n\\ kA^{k} &A^k \end{pmatrix} =\begin{pmatrix} A^{k+1} & 0_n\\ (k+1)A^{k+1}& A^{k+1} \end{pmatrix} $$ Par linéarité, si $P =\dsum_{k=0}^N a_kX^k$, alors: $$P(B) =\begin{pmatrix} \dsum_{k=0}^N a_kA^k&0_n\\ A\times \dsum_{k=0}^N a_kkA^{k-1}&\dsum_{k=0}^N a_kX^k \end{pmatrix} =\begin{pmatrix} P(A)&0_n\\ A P'(A)& P(A) \end{pmatrix}.$$
Soient $A,\,B\in \MM_n(\K)$ telles que $AB=BA$. Montrer que si $P,\,Q\in \K[X]$ alors $P(A)$ et $Q(B)$ commutent.
Supposons que $A$ et $B$ commutent. On a alors
$$A^2B=A.AB=A.BA=AB.A=BA.A=BA^2,$$
puis par récurrence immédiate,
$$\forall k\in \N,\quad A^kB=BA^k.$$
Par distributivité, $B$ commute ensuite avec tout polynôme en $A$.
En échangeant les rôles entre $B$ et $A$ : si $Q\in\K[X]$ alors $Q(B)$ commute avec $A$ d'après ce qui
précède, donc avec tout polynôme en $A$ !
On en déduit alors, si $A$ et $B$ commutent et $P,Q\in\C[X]$, alors $P(A)$ et $P(B)$ commutent.
- $\im u$ et $\Ker u$ sont stables par $v$.
- Pour tout $P \in \R[X]$, $\im (P(u))$ et $\Ker(P(u))$ sont stables par $v$.
- Pour tout $Q \in \R[X]$, $\im u$ et $\Ker u$ sont stables par $Q(v)$.
- Pour tous $P,Q \in \R[X]$, $\im (P(u))$ et $\Ker(P(u))$ sont stables par $Q(v)$.
Polynôme annulateur
-
Soient $u\in \LL (E)$ et $P\in \K[X]$.
On dit que $P$ est
un polynôme annulateur de $u$ (ou $P$ annule $u$) si $P(u)=0$.
on note $Ann(u)=\Ker(\varphi_u)=\{P \in \K[X] \, , \, P(u)= 0 \}$. -
Soient $A\in \mathscr{M}_n(\K)$ et $P\in \K[X]$.
On dit que $P$ est
un polynôme annulateur de $A$ (ou $P$ annule $A$ ) si $P(A)=0$.
on note $Ann(A)=\Ker(\varphi_A)=\{P \in \K[X] \, , \, P(A)= 0 \}$.
Soit $f$ un endomorphisme d'un espace vectoriel $E$ de dimension $n$.
- Montrer que $(\ide ,f,f^2 , \ldots ,f^{n^2 } )$ est liée.
- En déduire qu'il existe un polynôme non identiquement nul qui annule $f$.
On suppose que $f\neq 0$ (le cas $f=0$ est trivial). On sait que $\dim (\mathscr{L}(E))=\dim(E)^2=n^2$, la famille $\{f^j,\,j\in \inter{0,n^2}\}$ comporte $n^2+1$ éléments donc c'est une famille liée dans $\mathscr{L}(E)$. On en déduit qu'il existe $\alpha_0,\cdots,\alpha_{n^2}\in \K$ non tous nuls tels que $\dsum_{k=0}^{n^2}\alpha_jf^j=0$. On pose alors $P(X)=\dsum_{k=0}^{n^2}\alpha_kX^k$ alors $P\neq 0$ et $P(f)=0$.
Soient $a,\,b\in \C$. On considère la matrice $$M(a,b)=\begin{pmatrix} b&a&a&\cdots&a\\ a&b&a&\cdots&a\\ \vdots&\ddots&\ddots&\ddots&\vdots\\ a&\cdots&a&b&a\\ a&\cdots&a&a&b \end{pmatrix}.$$
- On définit le polynôme $Q_{a,b}\in \C[X]$ par $Q_{a,b}(X)=(X-(b-a))(X-(b+(n-1)a))$. Montrer que $Q_{a,b}$ est un polynôme annulateurde $M(a,b)$ et en déduire que $M(a,b)$ est diagonalisable (on distinguera les cas $a=0 $ et $a\neq 0$).
- Soit $k\in \N^*$. On suppose que $a\neq 0$. Déterminer le reste de la division euclidienne du polynôme $X^k$ par le polynôme $Q_{a,b}$ et en déduire une expression de $M(a,b)^k$ comme combinaison linéaire de $M(a,b)$ et de $I_n$.
- Supposons que $|b-a| < 1$ et $|b+(n-1)a|< 1$.Déterminer la limite de la suite de matrices $(M(a,b)^k)_{k\in N}$.
-
On note $J\in \MM_n(\C)$ la matrice tel que les coefficients de $J$ sont égales à $1$. Un calcul simple donne
$J^2=nJ$. Puis, on écrite, pour tout $(a,b)\in \C^2$,
$$M(a,b)=(b-a)I_n+aJ \Longrightarrow M(a,b)^2 = (b-a)^2I_n +2a(b-a)J +a^2J^2=(b-a)^2I_n+(2a(b-a)+na^2)J.$$
On écrit ensuite (on note $M=M(a,b)$ pour simplifier l'écriture):
$$
\begin{array}{lcl}
M^2&=& (b-a)^2I_n +a(b-a)J + (b-a+na)(aJ)\\
&=& (b-a)M +(b+(n-1)a) \left(aJ+(b-a)I_n-(b-a)I_n\right)\\
&=& (b-a)M +(b+(n-1)a)M - (b+(n-1)a)(b-a)I_n
\end{array}
$$
Ce qui donne,
$$0 = M^2- ((b-a)+(b+(n-1)a))M +(b+(n-1)a)(b-a)I_n =(M-(b-a)I_n)(M-(b+(n-1)a)I_n) =Q_{a,b}(M)$$
Ainsi, $Q_{a,b}$ est un polynôme annulateur de $M(a,b)$.
Si $a=0$ alors $M(0,b)=bI_n$ est diagonale donc diagonalisable :). Si $a\neq 0$ alors $M(a,b)$ admet un polynôme annulateur scindé à racine simple donc d'après le cours elle est diagonalisable - D'après le théorème de la division euclidienne dans $\C[X]$, il existe un unique couple $(P,R)\in \C^2[X]$ tel que $$X^k = P Q_{a,b}+R \text{ et } \deg(R) < \deg(Q_{a,b})$$ donc il existe un unique couple $(\alpha,\,\beta)\in \C^2$ tels que $$X^k = P Q_{a,b}+\alpha X +\beta\Longrightarrow \forall z\in \C,\quad z^k = P(z)Q_{a,b}(z)+\alpha z+\beta$$ Ce qui donne, pour $z=b-a$ puis $z= b+(n-1)a$, $$\left\{ \begin{array}{lcl} (b-a)\alpha +\beta &=& (b-a)^k\\ &&\\ (b+(n-1)a)\alpha +\beta &=& (b+(n-1)a)^k \end{array} \right. \Longrightarrow \left\{\begin{array}{lcl} \alpha &=& \dfrac{(b+(n-1)a)^k-(b-a)^k}{na},\quad\quad (a\neq 0)\\ &&\\ \beta &=& \dfrac{(b-a)^k(b+(n-1)a)-(b+(n-1)a)^k(b-a)}{na} \end{array} \right. $$ On en déduit alors $$M(a,b)^k = \dfrac{(b+(n-1)a)^k-(b-a)^k}{na} \,M(a,b)+ \dfrac{(b-a)^k(b+(n-1)a)-(b+(n-1)a)^k(b-a)}{na}\,I_n.$$
- Puisque $\abs{b-a} < 1$ alors $(b-a)^k\tendvers{k}{\infty}\,0$, de même $(b+(n-1)a)^k\tendvers{k}{\infty}0$. Ce qui donne $M(a,b)^k \tendvers{k}{\infty} 0$.
- soit $\varphi_u$ est injective, et $Ann(u)=\{0\}$.
- soit $\varphi_u$ n'est pas injective : il existe alors un et un seul polynôme normalisé (non nul), noté $\Pi_u$, tel que $Ann(u)$ soit exactement l'ensemble des polynômes multiples de $\Pi_u$.
$\Pi_u$ s'appelle alors le
-
Le polynôme minimal d'un endomorphisme $u$ (
s'il existe ) est donc caractérisé par : $\begin{cases} \Pi_u \neq 0 \textrm{ et } \Pi_u \textrm{ normalisé} \\ \Pi_u(u) = 0_{\mathscr{L}(E)} \\ \forall P \in \K[X], \ P(u)= 0_{\mathscr{L}(E)} \Rightarrow P \textrm{ multiple de } \Pi_u \end{cases}$ - Le polynôme minimal d'une matrice $M$ est donc caractérisé par : $\begin{cases} \Pi_M \neq 0 \textrm{ et } \Pi_M \textrm{ normalisé} \\ \Pi_M(M) = 0_{\MM_n(\K)} \\ \forall P \in \K[X], \ P(M)= 0_{\MM_n(\K)} \Rightarrow P \textrm{ multiple de } \Pi_M \end{cases}.$
- Le polynôme minimale ne fait plus partie de nouveau programme de PSI.
- Si $p$ est un projecteur de $E$, $p\neq 0$ et $p\neq Id_E$, le polynôme minimal de $p$ est : $X^2-X$.
- Si $s$ est une symétrie de $E$, $s\neq Id_E$ et $s\neq -Id_E$, le polynôme minimal de $s$ est : $X^2-1$.
- Le polynôme minimal d'un endomorphisme nilpotent d'indice $p$ est : $X^p$.
- Un endomorphisme peut ne pas posséder de polynôme minimal. Exemple : l'endomorphisme $u$ de $\K[X]$ qui à tout polynôme $P$ associe son polynôme dérivé $P'$.
-
Si $E$ est un $\K$-ev
de dimension finie, tout endomorphisme $u \in \mathscr{L}(E)$ possède un polynôme minimal. - Soient $n\in \N^*$ et $A\in \MM_n(\K)$, $A$ possède un polynôme minimal.
- Si deux matrices carrées $A$ et $A'$ sont semblables, alors $\Pi_A=\Pi_{A'}$. Plus généralement, si $P$ est un polynôme annulateur de $A$ alors $P(A')=0$.
- Si $A\in \MM_n(\K)$, $\Pi_A=\Pi_{^t A}$. Plus généralement, si $P$ est un polynôme annulateur de $A$ alors $P({^t A})=0$.