Intégrales impropres

Intégrales impropres

Rappels cours 1ère année

Soit $f\in \CC(I,\K)$ et $F$ une primitive de $f$ (on sait que $f$ admet des primitives sur $I$ ), on appelle intégrale de $f$ sur $I$ le réel $F(b)-F(a)$ et on note $\int_a^bf(t)\ud t=\left[F(t)\right]_a^b=F(b)-F(a).$

Soient $x_0\in I,\,f\in \CC(I,\K)$ , alors l'application $\fonct{F}{I}{\K}{x}{\dsp\int_{x_0}^xf(t)\ud t}$ est l'unique primitive de $f$ sur $I$ qui s'annule en $x_0$ .

Soient $f,g\in \CC^1(I,\K)$ , on a $%\label{IPP:segment} \int_a^bf'(t)g(t)\ud t =\left[f(t)g(t)\right]_a^b-\int_a^b f(t)g'(t)\ud t.$

Remarque

Généralement on utilise l'IPP lorsque $fg'$ est plus facile que $f'g$ à intégrer.

Soit $f\in \CC(I,\K)$ et $\varphi :[\alpha,\beta]\longmapsto \R$ une fonction de classe $\CC^1$ telle que $\varphi([\alpha,\beta])\subset I$ . Alors $% \label{ChangVar:segment} \int_\alpha^\beta f(\varphi(u))\varphi'(u)\ud u= \int_{\varphi(\alpha)}^{\varphi(\beta)}f(t)\ud t.$

Remarque

Dans le théorème précédent, il n'y a pas d'exigence sur la monotonie de $\varphi$ (bien que en générale, on choisit $\varphi$ strictement monotone). On verra dans les intégrales des fonctions continues par morceaux, qu'on exigera que $\varphi$ soit strictement monotone.

Fonctions continues par morceaux

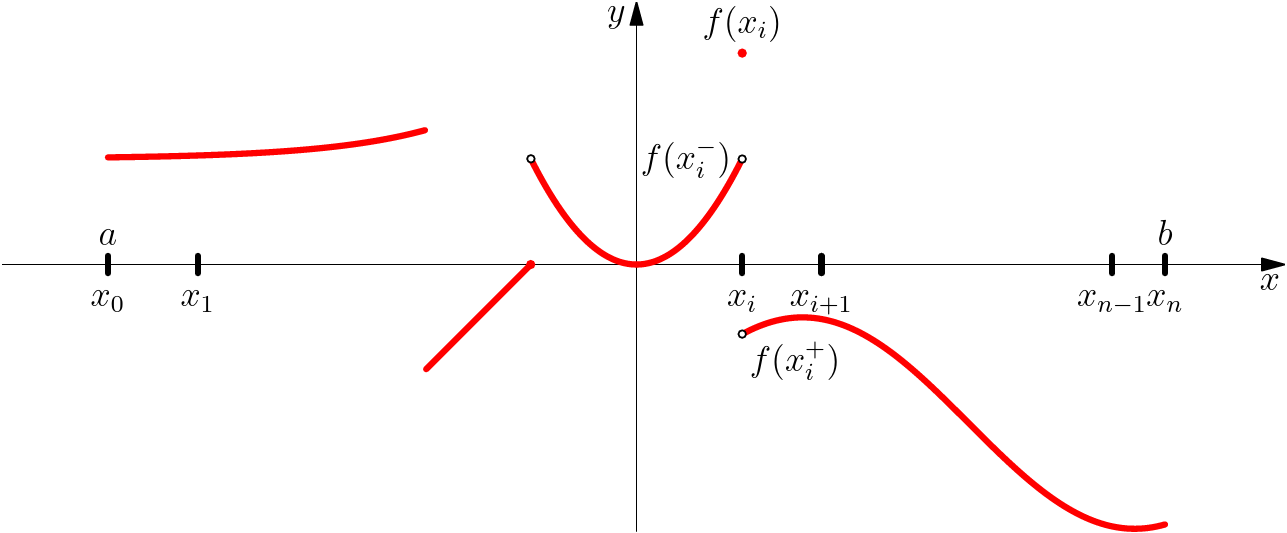
Soient $a< b$ deux réels. On rappel qu'une subdivision $\sigma =(x_i)_{0\leq i\leq n}$ de $[a,b]$ est un ensemble de points de $[a,b]$ vérifiant: $a=x_0< x_1< \cdots< x_{n-1}< x_n=b,\quad\quad\text{avec } n\in \N^*.$

Soit $f$ une application de $[a,b]$ à valeur dans $\K$ ; On dit que $f$ est continue par morceaux sur $[a,b]$ s'il existe $n\in \N^*$ et une subdivision $\sigma =(x_i)_{0\leq i\leq n}$ de $[a,b]$ tel que, pour tout $i\in \inter{0,n-1}$ , la restriction de $f$ à $]x_i,x_{i+1}[$ soit prolongeable par continuité sur $[x_i,x_{i+1}]$ .
On dit que $\sigma$ est une subdivision adaptée à $f$ .

Remarques

$f$ est continue par morceaux implique que $f\in \CC(]x_i,x_{i+1}[)$ et $f$ admet une limite finie en $x_i^+$ et une limite finie en $x_{i+1}^-$ .
Une fonction continue par morceaux est donc continue sur $[a,b]$ sauf en nombre fini de points de $[a,b]$ , et admet des limite finie à droite et à gauche en chacun de ces points.
Ceci implique donc qu'une fonction continue par morceau sur un segment est une fonction bornée, mais contrairement à une fonction continue, elle n'atteint pas forcement ses bornes.
La subdivision $\sigma$ n'est pas unique. Et une subdivision adaptée à $f$ doit contenir les points de discontinuité de $f$ .

Exemple graphique d’une fonction continue par morceaux sur $[a,b]$ .

Exemples

La fonction $x\in [-1,1]\longmapsto E(x)$ (partie entier de $x$ ) est continue par morceaux sur $[-1,1]$ .
Plus généralement une fonction en escalier sur $[a,b]$ est une fonction continue par morceaux.
La fonction $x\in [-1,1]\setminus\{0\}\longmapsto\dfrac{1}{x}$ n'est pas continue par morceaux sur $[-1,1]$ .

On notera dans la suite $\CC_M([a,b],\K)$ l'ensemble des fonctions continues par morceau sur $[a,b]$ à valeur dans $\K$ .

$\CC_M([a,b],\K)$ est un sous-espace vectoriel de $\mathcal{F}([a,b],\K)$ .

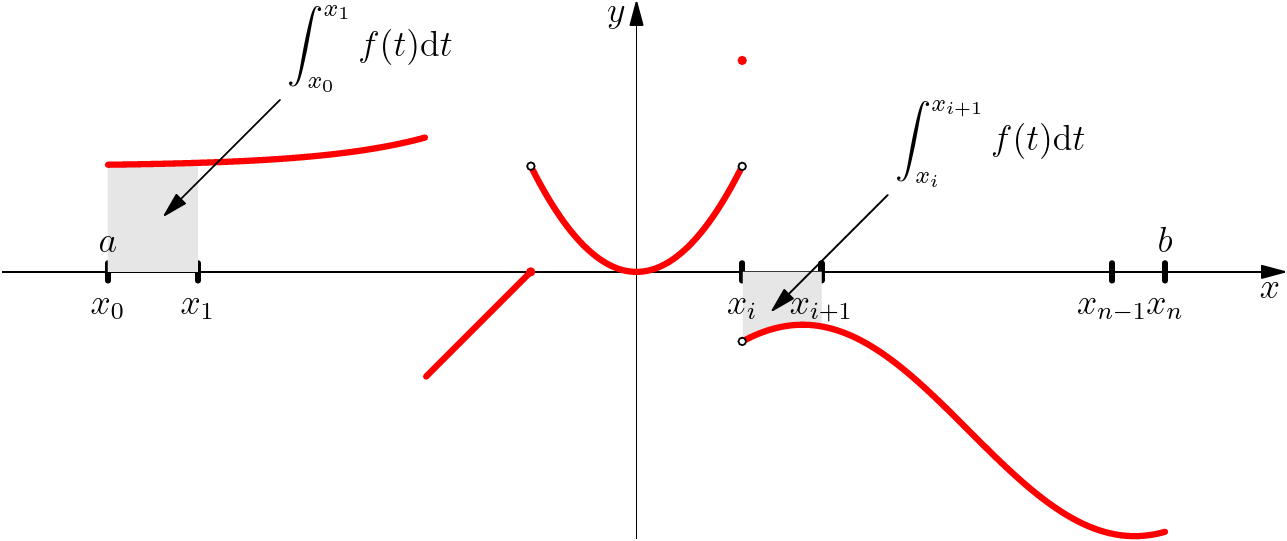
Soit $f$ une fonction continue par morceaux sur $[a,b]$ et $\sigma=(x_i)$ une subdivision adaptée à $f$ , $\dsp\int_{x_i}^{x_{i+1}}f$ a un sens (bien définie) puisque $f$ est prolongeable par continuité sur $[x_i,x_{i+1}]$ .

Calcul de $I(f,\sigma)$ .

Soient $\sigma_1,\,\sigma_2$ deux subdivisions adaptées à $f$ , alors $I(f,\sigma_1)=I(f,\sigma_2)$ .
En d'autre terme, le scalaire $I(f,\sigma)$ ne dépend que de la fonction $f$ .

Remarque

En notant $a_0=a < a_1 < \cdot < a_p=b$ les éventuels points de discontinuité de $f$ , alors pour tout $\sigma=(x_i)_{0\leq i\leq n}$ une subdivision adaptée à $f$ , on a $n\geq p,\quad\forall k\in \inter{0,p},\,\,\,\exists! i_k\in \inter{0,n},\, a_k=x_{i_k}$ avec $i_0=0 < i_1 < \cdots < i_p=n$ . En utilisant donc la relation de Chasles, on trouve $I(f,\sigma)=\dsum_{i=0}^n\int_{x_i}^{x_{i+1}}f(t)\ud t=\dsum_{k=0}^{p-1}\dsum_{i=i_k}^{i_{k+1}-1}\int_{x_i}^{x_{i+1}}f(t)\ud t=\dsum_{k=0}^{p-1}\int_{x_{i_k}}^{x_{i_{k+1}}}f(t)\ud t=\dsum_{i=0}^{p-1}\int_{a_i}^{a_{i+1}}f(t)\ud t$

Soit $f$ une fonction continue par morceaux sur $[a,b]$ . On appelle intégrale de $f$ sur $[a,b]$ , et on note $\dsp\int_a^b f(t)\ud t,$ (ou $\dsp\int_{[a,b]}f$ ) le scalaire $I(f)=\dsum_{i=0}^{p-1}\int_{a_i}^{a_{i+1}}f(t)\ud t.$

L'application $\fonct{}{\CC_M([a,b],\K)}{\K}{f}{\dsp\int_a^b f}$ est linéaire.

Soit $f$ une fonction continue par morceaux sur $[a,b]$ et $c\in ]a,b[$ . Alors

$f_{\mid_{[a,c]}}$ (resp. $f_{\mid_{[c,b]}}$ ) est une fonction continue par morceaux sur $[a,c]$ (resp. sur $[c,b]$ ).
On a la relation suivante, $\int_a^bf(t)\ud t =\int_a^c f(t)\ud t+\int_c^b f(t)\ud t.$

Soit $f\in \CC_M([a,b],\R)$ . On suppose que $f\geq 0$ alors $\dsp\int_a^bf(t)\ud t\geq 0$ .
Soient $f,g\in \CC_M([a,b],\R)$ . On suppose que $f\leq g$ alors $\dsp\int_a^bf(t)\ud t\leq \dsp\int_a^b g(t)\ud t$ .
Soit $f\in \CC_M([a,b],\K)$ . On a $\abs{\dsp\int_a^bf(t)\ud t}\leq \int_a^b\abs{f(t)}\ud t.$

Remarques

Bien évidement ces relations sont valables si les bornes de l'intégrale sont dans le bon sens i.e. $a < b$ .
Contrairement à une fonction continue, on peut avoir $f\geq 0$ et $\dsp\int_a^b f=0$ sans que $f$ soit la fonction nulle. En effet, dans ce cas $f=0$ sauf 'éventuellement' en un nombre fini de points.
Ceci implique que si $f,g\in \CC_M([a,b],\K)$ qui ne différent qu'en un nombre fini de points alors $\dsp \int_a^bf =\int_a^bg$ .

Soit $f\in \CC_M([a,b],\K)$ . On appelle primitive de $f$ toute application $F\in \CC([a,b],\K)$ dérivable partout ou $f$ est continue avec $F'(x)=f(x)$ (si $f$ est continue en $x$ ).

Primitive de $f$ sur $[a,b]$ .

Soit $f\in \CC_M([a,b],\K)$ , $x_0\in I$ . On considère la fonction $\fonct{F}{I}{\K}{x}{\dsp\int_{x_0}^xf(t)\ud t}$ , alors:

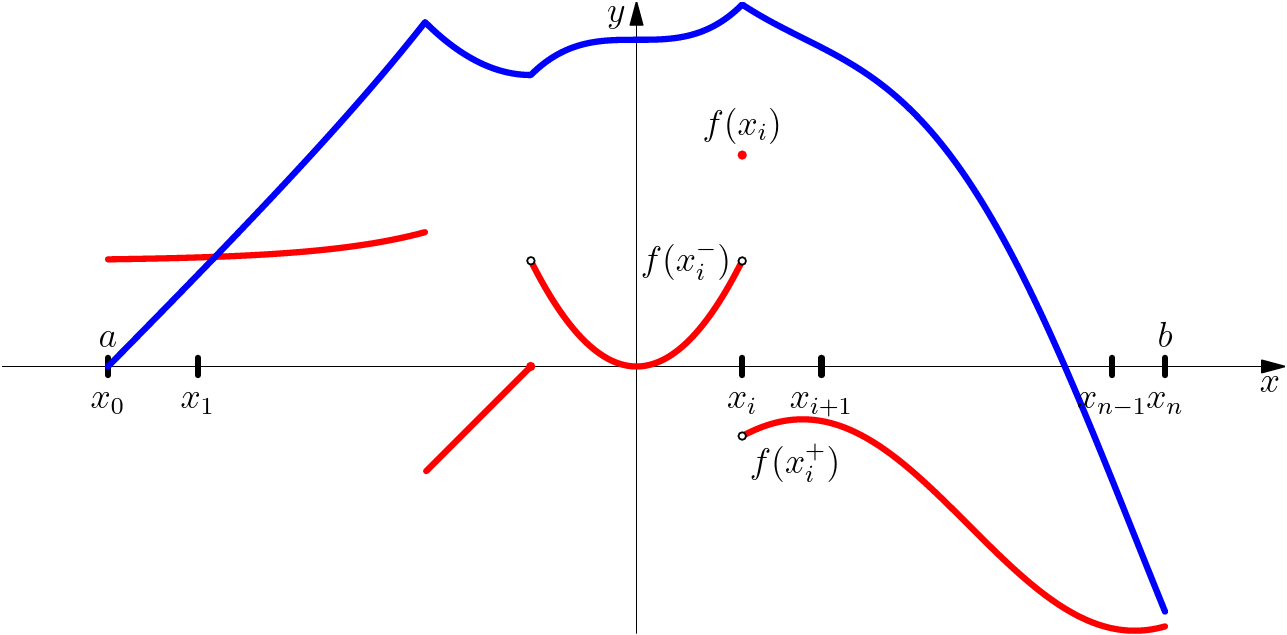
$F$ est continue sur $I$ .
$F$ est dérivable en tout point de $I$ ou $f$ est continue, et $F'(x)=f(x)$ .

Soit $\varphi :[\alpha,\beta]\longmapsto \R$ une fonction de classe $\CC^1$ strictement monotone et $f\in \CC_M(\varphi[\alpha,\beta]),\K)$ . Alors $%\label{ChangVar:CPM} \int_\alpha^\beta f(\varphi(u))\varphi'(u)\ud u= \int_{\varphi(\alpha)}^{\varphi(\beta)}f(t)\ud t.$

Soit $I$ un intervalle quelconque de $\R$ . On dit qu'une fonction $f$ définie sur $I$ à valeur dans $\K$ est continue par morceaux sur $I$ ssi pour tout segment $J$ inclus dans $I$ , $f\in \CC_M(J,\K)$ .
On note $\CC_M(I,\K)$ l'ensemble des fonctions continues par morceaux sur $I$ à valeur dans $\K$ .

Intégrales impropres: définitions

Soit $I$ un intervalle de $\R$ et $f\in \CC_M(I,\K)$ . On dit que $\dsp \int_I f$ est une intégrale impropre , dans les cas suivant:
$\mathbf{a)\quad\quad}$ $I$ n'est pas borné
ou
$\mathbf{b)\quad\quad}$ $I$ est borné mais pas un segment, et $f\not\in \CC_M(\overline{I},\K)$ .

Remarque

Il est important de ne pas confondre une intégrale bien défnie ( $I$ est un segment, $f\in \CC_M(I,K)$ ) avec une intégrale impropre

Soit $f\in \CC_M([a, b[,\K)$ avec $-\infty < a < b\leq +\infty$ . On dit que l'intégrale impropre (ou généralisée) $\dsp\int_a^b f(t) \ud t$ converge (ou existe) si: $\dsp\lim_{x\to b^{-}} \int_a^x f(t) \ud t\quad\text{existe}.$ S'il en est ainsi, cette intégrale est notée : $\dsp\int_a^b f(t) \ud t\quad\text{ou}\quad \dsp\int_a^b f \quad\text{ou}\quad\dsp\int_{[a,b[}f.$ Dans le cas contraire on dit que l'intégrale impropre $\dsp\int_a^b f$ diverge .

Remarque

Dans le cas ou $I$ est de la forme $]a,b]$ avec $-\infty\leq a < b < \infty$ , la définition de la convergence devient: $\int_a^bf(t)\ud t \text{ converge ssi } \dsp\lim_{x\to a^{+}} \int_x^b f(t) \ud t\quad\text{existe}.$

Exemples

$\dsp\int_0^1 \dfrac{\ud t}{1-t}$ est divergente. En effet, $t\longmapsto\dfrac{1}{1-t}\in \CC_M([0,1[,\R)$ et $\forall x\in ]0,1[,\quad \int_0^x\dfrac{\ud t}{1-t}=\left[-\ln(1-t)\right]_0^x=-\ln(1-x)\tendvers{x}{1^-}\,\infty.$
Pour tout $x>1$ , on a $x\longmapsto\frac{1}{x}\in \CC_M([1,\infty[,\R)$ et $\dsp\int_1^x\dfrac{\ud t}{t} =\ln(x)\tendvers{x}{\infty}\infty$ . Donc $\dsp\int_1^{+\infty}\dfrac{\ud t}t$ est divergente.
$\dsp\int_0^{+\infty}\dfrac{\ud t}{1+t^2}$ est convergente et vaut $\dfrac{\pi}2$ . Puisque $x\longmapsto\frac{1}{1+x^2}\in \CC_M(\R_+,\R)$ et $\forall x>0,\quad \dsp\int_0^{x}\dfrac{\ud t}{1+t^2}=\left[\Arctan(t)\right]_0^x=\Arctan(x)\tendvers{x}{\infty}\,\dfrac{\pi}{2}.$
$\dsp\int_0^1 \ln t \ud t$ est convergente et vaut $-1$ . En effet, $\ln \in \CC_M(]0,1],\R)$ et $\forall \varepsilon>0,\quad\int_\varepsilon^1\ln(t)\ud t=\left[t\ln(t)-t\right]_\varepsilon^1=-1-\varepsilon\ln(\varepsilon)+\varepsilon\tendvers{\varepsilon}{0^+}-1.$
$\dsp\int_0^1 \dfrac{\ud t}{\sqrt t}$ est convergente et vaut $2$ .

Remarque

Comme pour les séries numériques, on fera attention pour ne pas confondre l'objet 'intégrale impropre' $\dsp\int_a^b f(t)\ud t$ , il s'agit juste d'un symbole qui pourra avoir le statut convergence ou divergence, et il est impossible de l'utiliser dans les calculs tant que l'on n'a pas prouvé son existence, c'est-à-dire la convergence de l'intégrale.

Soit $f:\left[ {0, + \infty } \right[ \to \mathbb{R}_+$ continue par morceaux telle que $\dsp\int_0^\infty f$ converge. Montrer qu'il existe une suite $(x_n )$ de réels positifs vérifiant: $\dsp x_n \tendversN + \infty \text{ et }x_n f(x_n ) \tendversN 0$ .

Correction

Comme $\dsp\int_0^\infty f$ existe, alors $\forall \varepsilon>0,\quad \forall A>0, \quad \exists x\geq A, \quad xf(x)\leq \varepsilon.$ En effet, si cette relation n'est pas vérifiée, on aurait: $\exists \varepsilon_0>0,\quad \exists A>0,\,\,\forall x\geq A,\quad xf(x)>\varepsilon_0\Longrightarrow \forall x\geq A,\quad\int_A^x f(t)\ud t\geq \int_A^x\dfrac{\varepsilon_0\ud t}{t}.$ Ce qui contredit l'hypothèse.
En particulier, pour tout $n\in \N^*$ , il existe $x_n\geq n$ tel que $\abs{x_nf(x_n)}\leq \dfrac{1}{n}$ . Donc $\boxed{x_n f(x_n ) \tendversN 0}$ .

Fonctions de Riemann. Il s'agit des fonctions $t\mapsto \dfrac1{t^{\alpha}}$ pour $t>0$ et $\alpha\in \R$ .
$\mathbf{a. \,1)\quad\quad}$ $\dsp\int_0^1 \dfrac{\ud t}{t^{\alpha}}$ converge ssi $\alpha < 1$ .
$\mathbf{a. \,2)\quad\quad}$ $\dsp\int_1^{+\infty} \dfrac{\ud t}{t^{\alpha}}$ converge ssi $\alpha >1$ .
Exponentielle. $\dsp\int_0^{+\infty}\ee^{-at}\ud t$ converge ssi $a>0$ .
Logarithme. $\dsp\int_0^1 \ln t \ud t$ converge (et $\dsp\int_0^1 \ln t \ud t = -1$ ).

Soient $a$ et $b$ des réels tels que $a < b$ . Alors $\dsp\int_a^b \dfrac{\ud t}{(t-a)^{\alpha}}\quad\text { converge ssi }\quad \alpha < 1$

Soit $f\in \CC_M([a, b[,\K)$ avec $a$ et $b$ finis. Si $f$ admet une limite finie en $b^-$ , alors l'intégrale $\dsp\int_{[a,b[}f$ converge.
De plus, si on note $\tilde{f}$ le prolongement de $f$ par continuité en $b$ , on a $\dsp\int_{[a,b[} f = \dsp\int_a^b \tilde{f}$ .

Exemple

$\dsp\int_{\frac12}^1\dfrac{\ln t}{1-t}\ud t$ . En effet, $t\longmapsto \dfrac{\ln(t)}{1-t}\in \CC_M([1/2,1[,\R)$ et $\forall t\in [\frac{1}{2},1[,\,\dfrac{\ln(t)}{1-t}=-\dfrac{\ln(t)-\ln(1)}{t-1}\tendvers{t}{1}-\ln'(1)=-1.$

Remarques

Ce résultat n'est pas valable si $b=\infty$ , par exemple $\dfrac{1}{t}\tendvers{t}{\infty}0$ et pourtant $\dsp\int_1^\infty\dfrac{\ud t}{t}$ diverge.
On a un résultat analogue dans le cas ou $I$ est de la forme $]a,b]$ avec $-\infty < a < b < \infty$ .

Soit $f\in \CC_M([a, b[,\K)$ avec $-\infty < a < b\leq +\infty$ , et soit $c \in ]a, b[$ . L'intégrale impropre $\dsp\int_a^b f(t) \ud t$ converge si et seulement si l'intégrale impropre $\dsp\int_c^b f(t) \ud t$ converge et, dans ce cas : $\int_a^b f(t) \ud t = \int_a^c f(t) \ud t + \int_c^b f(t) \ud t.$

Remarques

Autrement dit, pour une fonction continue par morceaux sur $[a,b[$ , l'existence de l'intégrale dépend du comportement de $f$ au voisinage de $b$ .
Si $\dsp\int_a^bf$ converge alors $\dsp\int_x^bf\tendvers{x}{b^-}\,0$ .
Si $b=\infty$ , on peut faire le lien $\dsp\int_x^\infty f$ au reste d'une série numérique et entre $\dsp\int_a^xf$ et la somme partielle d'une séries numérique.

A la différence des séries numériques, il n'y pas de lien logique entre la convergence de $\dsp\int_a^\infty f$ et la limite de $f$ nulle en $\infty$ .
i.e. il se peut que $\dsp\int_a^{+\infty}f$ converge sans que $\dsp\lim_{t\to + \infty}f(t)$ soit nulle !!
c.f. exemple ci-après et l'exercice sur la convergence de $\dsp\int_0^\infty \sin(t^2)\ud t$ .
En revanche, ce que l'on peut affirmer : si $f$ admet une limite non nulle en $\infty$ alors $\dsp\int_a^x f$ diverge.

Exemple

Soit $f$ définie sur $\R_+$ par :
$\mathbf{--\quad}$ $f$ est continue et affine par morceaux.
$\mathbf{--\quad}$ $f(0)=0$
$\mathbf{--\quad}$ pour tout entier $n\geq 1$ , $f\left(n-\dfrac1{2n^3}\right)=f\left( n+\dfrac1{2n^3}\right)=0$ et $f(n)=n$

Cas d'un intervalle ouvert Soit $f\in \CC_M(]a, b[,\K)$ avec $-\infty \leqslant a < b \leqslant +\infty$ . On dit que l'intégrale impropre $\dsp\int_a^b f$ converge ssi il existe $c\in ]a,b[$ tels que les deux intégrales $\dsp\int_a^cf$ et $\dsp\int_c^b f$ sont convergentes.
Dans ce cas, on pose: $\int_a^b f(t)\ud t=\dsp\int_a^c f(t) \ud t + \dsp\int_c^b f(t) \ud t.$ Dans le cas contraire on dit que $\dsp\int_a^b f$ diverge.

Remarques

Si $\dsp\int_a^b f$ converge, alors sa valeur ne dépend pas du choix de $c$ , en effet dans ce cas tous les réels de l'intervalle $]a,b[$ conviennent .
$\dsp\int_a^b f$ diverge signifie que l'une au moins des intégrales $\dsp\int_a^c f(t) \ud t$ ou $\dsp\int_c^b f(t) \ud t$ diverge.

Exemples

$\dsp\int_{-\infty}^{+\infty}\dfrac{\ud t}{1+t^2}$ est convergente, et vaut $\pi$ .
$\dsp\int_{-1}^1 \dfrac{\ud t}{\sqrt{1-t^2}}$ est convergente et vaut $\pi$ .
$\dsp\int_0^{+\infty}\dfrac{\ud t}{t}$ est divergente.

Soit $f\in \CC_M(]a, b[,\K)$ avec $-\infty \leqslant a < b \leqslant +\infty$ . On dit que l'intégrale impropre $\dsp\int_a^b f$ converge ssi il existe $c\in ]a,b[$ tels que les deux intégrales $\dsp\int_a^cf$ et $\dsp\int_c^b f$ sont convergentes.
Dans ce cas, on pose: $\int_a^b f(t)\ud t=\dsp\int_a^c f(t) \ud t + \dsp\int_c^b f(t) \ud t.$ Dans le cas contraire on dit que $\dsp\int_a^b f$ diverge .

Remarques

Si $\dsp\int_a^b f$ converge, alors sa valeur ne dépend pas du choix de $c$ , en effet dans ce cas tous les réels de l'intervalle $]a,b[$ conviennent .
$\dsp\int_a^b f$ diverge signifie que l'une au moins des intégrales $\dsp\int_a^c f(t) \ud t$ ou $\dsp\int_c^b f(t) \ud t$ diverge.

Exemples

$\dsp\int_{-\infty}^{+\infty}\dfrac{\ud t}{1+t^2}$ est convergente, et vaut $\pi$ .
$\dsp\int_{-1}^1 \dfrac{\ud t}{\sqrt{1-t^2}}$ est convergente et vaut $\pi$ .
$\dsp\int_0^{+\infty}\dfrac{\ud t}{t}$ est divergente.

Soit $f \in \CC(\R,\R)$ telle que $\dsp \lim_{x \rightarrow - \infty}{f(x)} = \lambda$ et $\dsp \lim_{x \rightarrow + \infty}{f(x)} = \mu$ . Montrer que $\dsp \int_{- \infty}^{+ \infty}{\big[ f(x+1)-f(x) \big] \ud x}$ existe, et calculer sa valeur.

Correction

Puisque $f\in \CC(\R)$ , on en déduit que $x\mapsto f(x+1)-f(x)$ est continue également.
Soient $a,b\in \R$ tel que $a < b$ . On a $\begin{array}{lcl} \dsp\int_a^b\left(f(t+1)-f(t)\right)\ud t&=&\dsp\int_a^bf(t+1)\ud t-\int_a^bf(t)\ud t=\int_{a+1}^{b+1}f(t)\ud t-\int_a^bf(t)\ud t\\ &=&\dsp\int_b^{b+1}f(t)\ud t-\int_a^{a+1}f(t)\ud t \end{array}$ Soit $\varepsilon>0$ , puisque $\dsp \lim_{x \rightarrow + \infty}{f(x)} = \mu$ , alors il existe $B$ tel que pour tout $t>B$ , on a $\abs{f(t)-\mu}\leq \varepsilon$ .
Supposons que $b>B$ , alors $\forall t\in [b,b+1],~~ \mu-\varepsilon\leq f(t)\leq \mu+\varepsilon\Longrightarrow \mu-\varepsilon\leq \int_b^{b+1}f(t)\ud t\leq \mu+\varepsilon$ on en déduit que $\dsp \lim_{b \rightarrow + \infty}{\int_b^{b+1}f(x)\ud x} = \mu$ . De même, on montre que $\dsp \lim_{a \rightarrow - \infty}{\int_a^{a+1}f(x)\ud x} = \lambda$ .
On en déduit que $\dsp\int_\R(f(x+1)-f(x))\ud x$ existe et que $\boxed{\int_\R (f(x+1)-f(x))\ud x=\mu-\lambda}.$

Remarque

Avec les hypothèses de la définition précédente, soit $F$ une primitive de $f$ sur $]a,b[$ et soit $c\in ]a,b[$ .
Dire que l'intégrale $\dsp\int_a^c f$ existe équivaut à dire que $\dsp\lim_{x\to a^+}F(x)$ existe; et dans ce cas, on a $\dsp\int_a^c f = F(c)-\dsp\lim_{x\to a^+}F(x)$ .
Dire que l'intégrale $\dsp\int_c^b f$ existe équivaut à dire que $\dsp\lim_{y\to b^-}F(y)$ existe; et dans ce cas, on a $\dsp\int_c^b f = \dsp\lim_{y\to b^-}F(y)-F(c)$ .
Ainsi, dire que $\dsp\int_a^b f$ existe équivaut à dire que $F$ admet une limite en $a^+$ ET en $b^-$ ; et dans ce cas, on aura $\dsp\int_a^b f(t)\ud t = \dsp\lim_{\substack{x\to a^+\\y\to b^-}}\big[F(t)\big]_x^y =\dsp\lim_{b^-}F-\dsp\lim_{a^+}F$ que l'on notera parfois abusivement $\big[F(t)\big]_a^b$ (mais cette écriture n'est autorisée qu'après avoir justifié l'existence des deux limites).
On prendra garde à ne pas simplifier la définition! Par exemple, il ne faut pas confondre $\dsp\int_{-\infty}^{+\infty}t\ud t$ (qui diverge!) avec $\dsp\lim_{x\to + \infty}\dsp\int_{-x}^x t\ud t$ (qui vaut $0$ ).

Intégrales impropres: propriétés

Soit $f$ et $g$ deux fonctions continues par morceaux sur $[a, b[$ à valeurs dans $\K$ et $\lambda$ et $\mu$ deux scalaires. On suppose que les intégrales $\dsp\int_a^b f(t) \ud t$ et $\dsp\int_a^b g(t) \ud t$ convergent.
Alors l'intégrale impropre $\dsp\int_a^b \left( \lambda f + \mu g \right)(t) \ud t$ converge et : $\int_a^b \left( \lambda f + \mu g \right)(t) \ud t = \lambda \int_a^b f(t) \ud t + \mu \int_a^b g(t) \ud t.$ En d'autres termes: le sous-ensemble de $\CC_M([a,b],\K)$ formé des fonctions dont l'intégrale converge est un sev de $\CC_M([a,b],\K)$ , et sur cet espace, l'application $f\mapsto \dsp\int_a^b f$ est une forme linéaire.

Remarques

Il résulte immédiatement de la proposition précédente que, si $f$ a une intégrale divergente sur $[a,b[$ et $g$ une intégrale convergente, alors l'intégrale de $f+g$ sera divergente.
On ne peut cependant rien dire a priori de la somme de deux intégrales divergentes.
On fera très attention à ne pas écrire $\dsp\int_a^b(f+g)=\dsp\int_a^b f +\dsp\int_a^b g$ avant d'avoir étudié la convergence de ces deux intégrales!
Par exemple, l'écriture $\underbrace{\dsp\int_1^{+\infty}\dfrac{\ud t}{t(t+1)}}_{\text{CV}}=\underbrace{\dsp\int_1^{+\infty}\dfrac{\ud t}{t}}_{\text{DV}} - \underbrace{\dsp\int_1^{+\infty}\dfrac{\ud t}{t+1}}_{\text{DV}}\text{ N'A AUCUN SENS!!!}$ Comment faire alors?

Étudier la convergence de $\dsp\int_0^\infty\dfrac{\ud t}{(t+1)(t+2)(t+3)}$ et calculer sa valeur en cas de convergence.

Correction

La fonction $x\longmapsto\dfrac{1}{(x+1)(x+2)(x+3)}$ est continue sur $]0,\infty[$ , de plus, $\forall x\geq 0,\,\dfrac{1}{(x+1)(x+2)(x+3)}=\dfrac{A}{x+1}+\dfrac{B}{x+2}+\dfrac{C}{x+3}\overset{\text{\small après calculs}}{=}\dfrac{\frac{1}{2}}{x+1}+\dfrac{-1}{x+2}+\dfrac{\frac{1}{2}}{x+3}.$ Puisque on n'a pas le droit d'écrire $\int_0^\infty\dfrac{\ud t}{(t+1)(t+2)(t+3)} = \int_0^\infty\dfrac{\ud t}{2(t+1)}-\int_0^\infty\dfrac{\ud t}{(t+2)}+\int_0^\infty\dfrac{\ud t}{2(t+3)}$ car c'est faux tout simplement! Alors, on prend $X>0$ et on écrit $\begin{array}{lcl} \dsp\int_0^X\dfrac{\ud t}{(t+1)(t+2)(t+3)} &=&\dsp \int_0^X\dfrac{\ud t}{2(t+1)}- \int_0^X\dfrac{\ud t}{(t+2)}+\int_0^X\dfrac{\ud t}{2(t+3)}\\ &=&\dsp\left[\frac{1}{2}\ln(\abs{t+1})\right]_0^X-\left[\ln(\abs{t+2})\right]_0^X+\left[\frac{1}{2}\ln(\abs{t+3}\right]_0^X\\ &=&\dsp\ln\left(\dfrac{\sqrt{(X+1)(X+3)}}{X+2}\right) +\ln(2)-\ln(\sqrt{3}). \end{array}$ Etant donné que $\ln\left(\dfrac{\sqrt{(X+1)(X+3)}}{X+2}\right)\tendvers{X}{\infty}\ln(1)=0$ , on en déduit que $\int_0^X\dfrac{\ud t}{(t+1)(t+2)(t+3)}\tendvers{X}{\infty} \ln\left(\dfrac{2}{\sqrt{3}}\right)$ Ce qui prouve la convergence de l'intégrale.

Remarque

On verra dans la partie suivante des méthode permettent de diagnostiquer rapidement la convergence de cette intégrale.

Soit $f$ une fonction continue par morceaux sur $[a,b[$ , à valeurs réelles. Si $f\geq 0$ sur $[a,b[$ et si l'intégrale de $f$ est convergente, alors $\dsp\int_a^b f(t)\ud t \geq 0$ .
Soient $f$ et $g$ deux fonctions continues par morceaux sur $[a,b[$ , à valeurs réelles. Si $f(t)\leq g(t)$ pour tout $t\in [a,b[$ et si les intégrales de $f$ et de $g$ c onvergent, alors $\dsp\int_a^b f(t)\ud t \leq \dsp\int_a^b g(t)\ud t$ .

Soit $f$ une fonction continue sur $[a,b[$ , à valeurs réelles positives}, telle que l'intégrale de $f$ sur $[a,b[$ est convergente. Alors : $\dsp\int_a^b f(t)\ud t =0 \Longrightarrow f=0\text{ sur } [a,b[.$

Soit $f$ une fonction continue par morceaux sur $[a,b[$ , à valeurs dans $\C$ . Pour que l'intégrale de $f$ sur $[a,b[$ soit convergente, il faut et il suffit que les intégrales de $\re(f)$ et de $\im(f)$ le soient, et, dans ce cas on a $\dsp\int_a^b f(t)\ud t = \dsp\int_a^b \re(f(t))\ud t + \ii \dsp\int_a^b \im(f(t))\ud t$

Soit $f$ une fonction continue par morceaux sur $[a,b[$ , à valeurs dans $\C$ . Si l'intégrale $\dsp\int_a^b f(t)\ud t$ est convergente, il en est de même de $\dsp\int_a^b \overline{f(t)}\ud t$ et on a $\dsp\int_a^b \overline{f(t)}\ud t = \overline{\dsp\int_a^b f(t)\ud t}$

Cas des fonctions positives

Soit $f$ continue par morceaux sur $[a,b[$ , avec $-\infty \leq a < b< \leq +\infty$ , à valeurs réelles positives.
Soit $F$ l'application $\fonct{F}{[a,b[}{\R}{x}{\dsp\int_a^x f(t)\ud t}$ . Alors l'intégrale $\dsp\int_a^b f(t)\ud t$ converge ssi $F$ est majorée.
Dans ce cas, $\dsp\int_a^b f(t)\ud t=\dsp\lim_{x\to b^-}F(x)$ . Dans le cas contraire, $\dsp\lim_{x\to b^-}\dsp\int_a^x f(t)\ud t = +\infty$ .

Remarque

Dans le cas d'une fonction définie sur un intervalle de la forme $]a,b]$ avec $-\infty\leq a < b < +\infty$ et à valeurs réelles positives, la fonction $x\mapsto \dsp\int_x^b f(t)\ud t$ est décroissante.
Elle admet donc une limite en $a^+$ ssi elle est majorée: on obtient donc un résultat tout à fait similaire. Pour cette raison, les théorèmes de comparaison qui vont suivre restent entièrement valables dans le cas où l'intervalle d'intégration est de la forme $]a,b]$ .

Soient $f$ et $g$ continues par morceaux sur $[a,b[$ , avec $-\infty < a < b\leq +\infty$ , à valeurs réelles. On suppose qu'il existe $c\in [a,b[$ tel que: $\forall t\in [c,b[\ , \ 0\leq f(t)\leq g(t)$ Alors:

Si $\dsp\int_a^b g(t)\ud t$ converge, alors $\dsp\int_a^b f(t)\ud t$ converge (et on a alors $\dsp\int_c^b f \leq \dsp\int_c^b g\,)$ .
Si $\dsp\int_a^b f(t)\ud t$ diverge, alors $\dsp\int_a^b g(t)\ud t$ diverge.

Rapport du jury -- CCP 2014, 2015,..
Certains éprouvent des difficultés à montrer la convergence d'une série ou d'une intégrale sur des exemples simples (et classiques). L'utilisation des théorèmes de comparaison, pour les séries ou les intégrales impropres, sans se soucier des questions de signe est sanctionnée.

Soient $f$ et $g$ continues par morceaux sur $[a,b[$ , avec $-\infty< a < b\leq +\infty$ , à valeurs réelles, positives au voisinage de $b$ .

Si $f\underset{b^-}{=}\mathrm{O}(g)$ et si $\dsp\int_a^b g(t)\ud t$ converge, alors $\dsp\int_a^b f(t)\ud t$ converge.
Si $f\underset{b^-}{=}\mathrm{o}(g)$ et si $\dsp\int_a^b g(t)\ud t$ converge, alors $\dsp\int_a^b f(t)\ud t$ converge.

Remarque

Comme la nature d'une intégrale ne change pas si on multiplie la fonction par un scalaire, on peut, dans les hypothèses de ce corollaire, remplacer la phrase « $f$ et $g$ sont positives au voisinage de $b$ » par « $f$ et $g$ sont de signes constants au voisinage de $b$ »

Comme pour les séries numériques, il faut s'assurer que $f$ et $g$ sont de signe constant au voisinage de $b$ .
Considérons l'exemple: $f(t)=\dfrac{\abs{\sin(t)}}{t},\,g(t)=\dfrac{\sin(t)}{\sqrt{t}}$ , on a bien $f\underset{\infty}{=}\mathrm{o}(g)$ , pourtant, $\dsp\int_1^\infty f(t)\ud t$ diverge et $\dsp\int_1^\infty g(t)\ud t$ diverge.

Soient $f$ et $g$ continues par morceaux sur $[a,b[$ , avec $-\infty< a< b\leq +\infty$ , à valeurs réelles. On suppose $g$ positive au voisinage de $b$ . S'il existe une constante réelle $k\neq 0$ telle que $f\underset{b^-}{\thicksim}kg$ , alors les intégrales de $f$ et $g$ sur $[a,b[$ sont de même nature.

Remarque

La condition « de signe constant » est indispensable. c.f. exemple ci-après.

Exemple

On pose $f(t)=\displaystyle {\frac {\sin (t)}{\sqrt {t}}}+{\frac {|\sin( t)|}{t}}{\text{ et }} g(t)={\frac {\sin (t)}{\sqrt {t}}}$ . On a $f\underset{\infty}{\thicksim}g$ mais leurs intégrales ne sont pas de même nature.

Soit $f\in \CC_M([a,\infty[,\R)$ à valeurs positives (au mois au voisinage de $\infty$ ). Alors

On suppose qu'il existe $k>0$ et $\alpha\in \R$ tels que $f(t)\underset{t\to \infty}{\thicksim}\dfrac{k}{t^\alpha}$ .
Si $\alpha>1$ alors $\dsp\int_a^\infty f(t)\ud t$ converge, sinon ( $\alpha\leq 1$ ) $\dsp\int_a^\infty f(t)\ud t$ diverge.
S'il existe $\alpha>1$ tel que $f(t)=\underset{t\to \infty}{\mathrm{O}}\left(\dfrac{1}{t^\alpha}\right)$ ou $f(t)=\underset{t\to \infty}{\mathrm{o}}\left(\dfrac{1}{t^\alpha}\right)$ , alors $\dsp\int_a^\infty f(t)\ud t$ converge.
S'il existe $k>0$ et $\alpha\leq 1$ tels que $f(t)\geq \dfrac{k}{t^\alpha}$ au voisinage de $\infty$ alors $\dsp\int_a^\infty f(t)\ud t$ diverge.

Exemple

Dans l'exercice \ref{Ex:(t+1)(t+2)}, on a $f(x)=\dfrac{1}{(x+1)(x+2)(x+3)}\underset{x\to \infty}{\thicksim}\dfrac{1}{x^3}$ donc d'après le résultat précédent $\dsp\int_1^\infty f(x)\ud x$ converge.

Remarque

On peut facilement adapter ce résultat au cas ou $I=[a,b[$ avec $b$ fini, en utilisant les fonctions de références $\dfrac{1}{(t-b)^\alpha}$
On peur obtenir le 3\up{ème} cas en montrant que $xf(x)\tendvers{x}{\infty}\infty$ .
...

Soient $a>0$ et $f\in \CC_M(]0,a],\R)$ à valeurs positives (au mois au voisinage de $0^+$ ). Alors

On suppose qu'il existe $k>0$ et $\alpha\in \R$ tels que $f(t)\underset{t\to 0}{\thicksim}\dfrac{k}{t^\alpha}$ .
Si $\alpha < 1$ alors $\dsp\int_0^a f(t)\ud t$ converge, sinon ( $\alpha\geq 1$ ) $\dsp\int_0^a f(t)\ud t$ diverge.
S'il existe $\alpha < 1$ tel que $f(t)=\underset{t\to 0}{\mathrm{O}}\left(\dfrac{1}{t^\alpha}\right)$ ou $f(t)=\underset{t\to 0}{\mathrm{o}}\left(\dfrac{1}{t^\alpha}\right)$ , alors $\dsp\int_0^a f(t)\ud t$ converge.
S'il existe $k>0$ et $\alpha\geq 1$ tels que $f(t)\geq \dfrac{k}{t^\alpha}$ au voisinage de $0$ alors $\dsp\int_0^a f(t)\ud t$ diverge.

Techniques de calcul d'une intégrale impropre

Utilisation de primitives

Si $f$ est continue par morceaux sur $]a,b[$ avec $-\infty \leq a < b \leq +\infty$ , et si $F$ est une primitive de $f$ , alors $f$ est intégrable sur $]a,b[$ si et seulement si $F$ admet des limites finies en $a^+$ et en $b^-$ , et on a alors~: $\int_{]a,b[}\!f = \lim_{x\to b^-} F(x) - \lim_{x\to a^+} F(x).$

Montrer que la fonction $x\mapsto \ln \dfrac{1}{x-x^2}$ est intégrable sur $]0,1[$ et calculer son intégrale.

Correction

Soit $\eps$ et $x$ dans $]0,1[$ . $\begin{array}{lcl} \dsp\int_{\eps}^x \ln\dfrac{1}{t-t^2} \ud t&= & \dsp\int_{\eps}^x \biggl( -\ln t-\ln(1-t) \biggr) \,\ud t\\ &= & \biggl[ -t\ln t+t+(1-t)\ln(1-t)-1+t \biggr]_{\eps}^x\\ &= & F(x)-F(\eps) \quad \text{avec} \quad F(x) = -x\ln x+(1-x)\ln(1-x)+2x-1 \end{array}$ $\lim\limits_0 F=-1$ ; $\lim\limits_1 F=1$ ; d'où : $\quad\dsp\int_0^1\ln\dfrac{1}{x-x^2} \ud x = 2$ .

Intégration par parties

Soient $f,g\in \CC^1([a,b[,\K)$ avec $-\infty< a< b\leq \infty$ . On suppose que $fg$ admet une limite finie en $b$ . Alors

Les intégrales $\dsp \int_a^bfg'$ et $\dsp\int_a^bf'g$ sont de même nature.
Si l'une d'elles converge, alors $\int_a^bf(t)g'(t)=\lim_{x\to b}(f(x)g(x))-f(a)g(a)-\int_a^bf'(t)g(t)\ud t.$

Exemple

Considérons l'exemple classique $\dsp\int_1^\infty\dfrac{\sin(t)}{t}\ud t$ .
On pose $f(t)=-\cos(t),\, g(t)=\dfrac{1}{t}$ , comme $f(t)g(t)\tendvers{t}{\infty}\,0$ , on en déduit alors que $\dsp\int_1^\infty \dfrac{\sin(t)}{t}\text{ et }\int_1^\infty \dfrac{\cos(t)}{t^2}\ud t \text{ sont de même nature}.$

Remarque

En générale, on utilise IPP lorsque le calcul de la primitive de $\varphi = f'g$ est plus facile que celui de $fg'$ . Ceci reste valable pour les intégrales impropres.
Ainsi il avoir le bon sens pour faire le choix de $f$ et $g$ i.e. il faut qu'on puisse déterminer la nature de $\dsp\int fg'$ facilement!
Dans l'exemple précédent, on aurait pu écrire: $\forall X>1,\quad \int_1^X\dfrac{\sin(x)}{x}\ud x=\left[\sin(x)\ln(x)\right]_1^X-\int_1^X\cos(x)\ln(x)\ud x.$ Un tel choix (bien que la formule est correcte!) ne permet pas de déterminer la nature de l'intégrale.

Nature de $\dsp\int_0^\infty\dfrac{\sin(x)}{\sqrt{x}}\ud x$ .

Correction

La fonction $f:x\longmapsto\dfrac{\sin(x)}{\sqrt{x}}$ est continue sur $]0,\infty[$ , de plus $\dfrac{\sin(x)}{\sqrt{x}}\tendvers{x}{0^+}\,0$ donc $\dsp\int_0^1 f$ existe.
Soit $X>1$ , on a $\int_1^Xf(x)\ud x=\left[\dfrac{-\cos(x)}{\sqrt{x}}\right]_1^X-\dfrac{1}{2}\int_1^X\dfrac{\cos(x)}{\sqrt{x^3}}\ud x= \cos(1)-\dfrac{\cos(X)}{\sqrt{X}}-\dfrac{1}{2}\int_1^X\dfrac{\cos(x)}{\sqrt{x^3}}\ud x.$ Or, $\dfrac{\cos(X)}{\sqrt{X}}\tendvers{X}{\infty}\,0$ et $\int_1^X\abs{\dfrac{\cos(x)}{\sqrt{x^3}}}\ud x\leq \int_1^X\dfrac{1}{\sqrt{x^3}}\ud x\leq \int_1^\infty\dfrac{1}{\sqrt{x^3}}\ud x \Longrightarrow \int_1^X\dfrac{\cos(x)}{\sqrt{x^3}}\ud x <\infty$ On en déduit alors que $\int_1^X\dfrac{\cos(x)}{\sqrt{x^3}}\ud x\tendvers{X}{\infty}\,\int_1^\infty\dfrac{\cos(x)}{\sqrt{x^3}}\ud x.$ Ce qui donne, $\int_1^Xf(x)\ud x\tendvers{X}{\infty}\,\cos(1)-\dfrac{1}{2}\int_1^\infty\dfrac{\cos(x)}{\sqrt{x^3}}\ud x$ autrement dit, $\dsp\int_1^\infty f(t)\ud t$ converge.

Ainsi, $\dsp\int_0^\infty \dfrac{\sin(t)}{\sqrt{t}}\ud t$ converge.

Changement de variable

Soit $f$ une fonction continue par morceaux sur un intervalle $]\alpha,\beta[$ à valeurs réelles ou complexes, et $\varphi$ une bijection d'un intervalle $]a,b[$ sur $]\alpha,\beta[$ , de classe $\CC^1$ sur $]a,b[$ .
Alors l'intégrale $\dsp\int_{\alpha}^{\beta} f$ est convergente ssi l'intégrale $\dsp\int_{a}^{b} (f\circ\varphi)\varphi'$ l'est, et, dans ce cas : $\int_\alpha^\beta f(t)\,\ud t = \int_a^b f\circ\varphi\,(u) \cdot \varphi'(u)\,\ud u.$

Nature de $\dsp\int_0^\infty \sin(t^2)\ud t$ .

Correction

On pose $\varphi(t)= \sqrt{t}$ , $\varphi\in \CC^1(]0,\infty[)$ et $\varphi'(t)=\dfrac{1}{2\sqrt{t}}>0$ donc $\varphi$ est un changement de variable bijectif de $]0,\infty[$ sur $]0,\infty$ .
Donc $\dsp\int_0^\infty\sin(t^2)\ud t$ et $\dsp\int_0^\infty\sin(\varphi(t)^2)\varphi(t)'\ud t$ sont de même nature, or $\int_0^\infty\sin(\varphi(t)^2)\varphi(t)'\ud t=\int_0^\infty\sin(\sqrt{t}^2)\dfrac{\ud t}{2\sqrt{t}}=\dfrac{1}{2}\int_0^\infty\dfrac{\sin(t)}{\sqrt{t}}\ud t$ D'après l'exercice précédent, cette dernière intégrale est convergente, on en déduit alors que $\dsp\int_0^\infty \sin(t^2)\ud t$ converge.

Remarques

Cet exemple montre encore qu'on peut avoir $\dsp\int_a^bf$ converge sans que $f$ admet une limite en $b$ .
En utilisant différentes méthodes, (c.f. Intégrales à paramètres ), on peut montrer que $\int_0^\infty\sin(t^2)\ud t=\int_0^\infty \cos(t^2)\ud t =\dfrac{\sqrt{2\pi}}{4}.$

Intégrales absolument convergentes

Définitions

Soit $f$ une fonction continue par morceaux sur un intervalle $[a, b[$ avec $-\infty< a< b\leq +\infty$ , à valeurs dans $\K$ .
On dit que l'intégrale $\dsp\int_a^b f(t)\ud t$ est absolument convergente si l'intégrale $\dsp\int_a^b \abs{f(t)}\ud t$ est convergente.
Lorsque l'intégrale $\dsp\int_a^b f(t)\ud t$ est absolument convergente, on dit aussi que $f$ est intégrable sur $[a,b[$ .

Remarques

On a une définition analogue dans le cas d'une fonction définie sur un intervalle de la forme $]a,b]$ ou $]a,b[$ .

Soit $f\in \CC_M([a, b[,\K)$ avec $-\infty< a< b\leq +\infty$ . Si l'intégrale $\dsp\int_a^b f$ est absolument convergente, alors elle est convergente, et on a $\abs{\dsp\int_a^b f(t)\ud t}\leq \dsp\int_a^b \abs{f(t)}\ud t$

Remarques

La réciproque du théorème précédent est fausse.
Il existe en effet des intégrales qui sont convergentes sans être absolument convergentes (une telle intégrale est dite semi-convergente ). Le contre-exemple est classique et doit être connu:

Montrer que $\dsp\int_0^{+\infty}\abs{\dfrac{\sin (t)}{t }}\ud t$ est divergente.

Correction

La fonction $t\longmapsto\abs{\dfrac{\sin (t)}{t }}$ est continue sur $]0,\infty[$ de plus elle admet une limite finie en $0^+$ , donc $\dsp\int_0^{1}\abs{\dfrac{\sin (t)}{t }}\ud t$ converge.
D'autre part, comme $\abs{\sin(t)}\in [0,1]$ , on en déduit que $\abs{\sin(t)}\geq \sin^2(t)$ , ce qui donne $\forall X>1,\quad\int_1^X\abs{\dfrac{\sin (t)}{t }}\ud t\geq \int_1^X\dfrac{\sin^2(t)}{t}\ud t= \int_1^X\left(\dfrac{1-\cos(2t)}{2t}\right)\ud t,$ or $\dsp\int_1^X\dfrac{\cos(2t)}{2t}\ud t$ tend vers une limite finie lorsque $X$ tend vers $\infty$ (en effet, $\dsp\int_1^\infty\dfrac{\cos(t)}{t}\ud t$ converge, démonstration similaire à l'exercice précédent), tandis que $\dsp\int_1^X\dfrac{1}{2t}\ud t=\ln(\sqrt{X})\tendvers{X}{\infty}\infty$ .
Ce qui donne $\dsp\int_1^\infty\dfrac{1-\cos(2t)}{2t}\ud t$ diverge et par conséquent $\dsp\int_1^\infty\abs{\dfrac{\sin (t)}{t }}\ud t$ diverge.
Conclusion $\dsp\int_0^\infty\abs{\dfrac{\sin (t)}{t }}\ud t$ diverge.

Soit $[a,b]$ un segment de $\R$ et $f\in \CC_M(]a,b[,\K)$ on suppose que $f$ est borné sur $]a,b[$ . Alors $\dsp\int_a^b f(x)\ud x$ est absolument convergente.

Exemple

La fonction $f(x)=\sin\left(\frac{1}{x}\right)$ est continue par morceaux sur $]0,1]$ et borné sur $]0,1]$ donc $\dsp\int_0^1f(x)\ud x$ converge.
On remarque dans cet exemple que $f$ n'admet pas de limite en $0^+$ .

Soient $f$ et $g$ continues par morceaux sur $[a,b[$ , avec $-\infty< a< b\leq +\infty$ . On suppose que $g$ à valeurs réelles positives au voisinage de $b$ .

Si $f\underset{b^-}{=}\mathrm{O}(g)$ et si $\dsp\int_a^b g(t)\ud t$ converge, alors $\dsp\int_a^b f(t)\ud t$ est absolument convergent.
Si $f\underset{b^-}{=}\mathrm{o}(g)$ et si $\dsp\int_a^b g(t)\ud t$ converge, alors $\dsp\int_a^b f(t)\ud t$ est absolument convergente.

Règle de Riemann Soit $f\in \CC_M([a,\infty[)$ . On suppose, $\exists \alpha>1,\quad\text{ tel que } f\underset{\infty}{=}\mathrm{O}(\frac{1}{x^\alpha})\text{ ou } f\underset{\infty}{=}\mathrm{o}(\frac{1}{x^\alpha})$ Alors $\dsp\int_a^\infty f$ est absolument convergente.

Règle de Riemann Soit $f\in \CC_M(]0,a])$ . On suppose, $\exists \alpha< 1,\quad\text{ tel que } f\underset{0}{=}\mathrm{O}(\frac{1}{x^\alpha})\text{ ou } f\underset{0}{=}\mathrm{o}(\frac{1}{x^\alpha})$ Alors $\dsp\int_0^a f$ est absolument convergente.

Exemples

Nature de $\dsp\int_0^{+\infty}\dfrac{\sin\sqrt x}{x\sqrt{1+x^2}}\ud x$ .
Nature de $\dsp\int_1^{+\infty}\ln\left(1+\dfrac{\sin x}{\sqrt x}+\dfrac{a}x\right)\ud x$ avec $a\in \R$ .

Norme de la convergence en moyenne

L'ensemble des fonctions continues par morceaux et intégrables sur un intervalle $I$ à valeurs dans $\K=\R$ ou $\C$ constitue un sous-espace vectoriel de $\CC_M(I,\K)$ , noté $L^{1}(I,\K)$ , et l'application $f\mapsto \dsp\int_I f$ est une forme linéaire sur cet espace vectoriel.

On note $E_1$ L'ensemble des fonctions continues et intégrables sur un intervalle $I$ à valeurs dans $\K$ , i.e. $E_1=\CC(I,\K)\cap L^{1}(I,\K)$ . Alors $E_1$ est un sous-espace vectoriel de $\CC(I,\K)$ .
L'application $N_1: f\mapsto \dsp\int_I\abs{f}$ est une norme sur $E_1$ , appelée norme de la convergence en moyenne.
La forme linéaire $f\mapsto \dsp\int_I f$ est une forme linéaire continue sur l'espace vectoriel normé $(E_1,N_1)$ .

Norme de la convergence en moyenne quadratique

Une fonction $f$ continue par morceaux sur $I$ et à valeurs dans $\R$ est dite de carré intégrable si $|f|^2$ est intégrable sur $I$ .
On note $L^2(I,\R)=\{f\in \CC_M(I,\R),\text{t.q. } |f|^2\in L^1(I,\R)\}$ .

$L_2(I,\R)$ est un sous-espace vectoriel de $\CC_M(I,\R)$ .
L'ensemble des fonctions continues de carré intégrable sur $I$ constitue un sous-espace vectoriel de $\CC(I,\R)$ , que l'on note $E_2$ .
L'application $\fonct{\varphi}{E_2^2}{\R}{(f,g)}{\dsp\int_Ifg}$ définit un produit scalaire sur $E_2$ .
La norme associée à ce produit scalaire est appelée norme de la convergence en moyenne quadratique: $\forall f\in E_2^2\ ,\ N_2(f) = \left(\dsp\int_{I}\!|f|^2\right)^\frac12.$

Exemples

La fonction $f:x\longmapsto\dfrac{1}{\sqrt{x}}\in E_1(]0,1],\R)$ mais $f\not \in E_2(]0,1],\R)$ .
La fonction $f:x\longmapsto\dfrac{1}{x}\not\in E_1([1,\infty[,\R)$ mais $f\in E_2([1,\infty[,\R)$ .

Le produit de deux fonctions $f$ et $g$ continues de carré intégrable sur $I$ est intégrable sur $I$ et: $\abs{\scal{f}{g}}=\abs{\dsp\int_Ifg}\leqslant N_1(fg) \leqslant N_2(f)N_2(g).$

Le produit scalaire $(f,g)\mapsto \scal{f}{g}$ est une application continue de $E_2(I,\R)^2$ dans $\R$ .

(Centrale 2022)

On note $E=\{f\in \CC(\R_+^*,\quad \dsp\int_0^\infty f^2(t)\dfrac{\ee^{-t}}{t}\ud t < \infty\}$ . Montrer que, si $f,g\in E$ alors $\dsp \int_0^\infty f(t)g(t)\dfrac{\ee^{-t}}{t}\ud t$ est absolument convergente.

Correction

Rapport du jury:

Q 9. : Résultat classique. Seul un tiers des candidats sait comment la traiter.