Calculs différentiels
Fonctions de classe $\CC^1$
Applications partielles, continuité
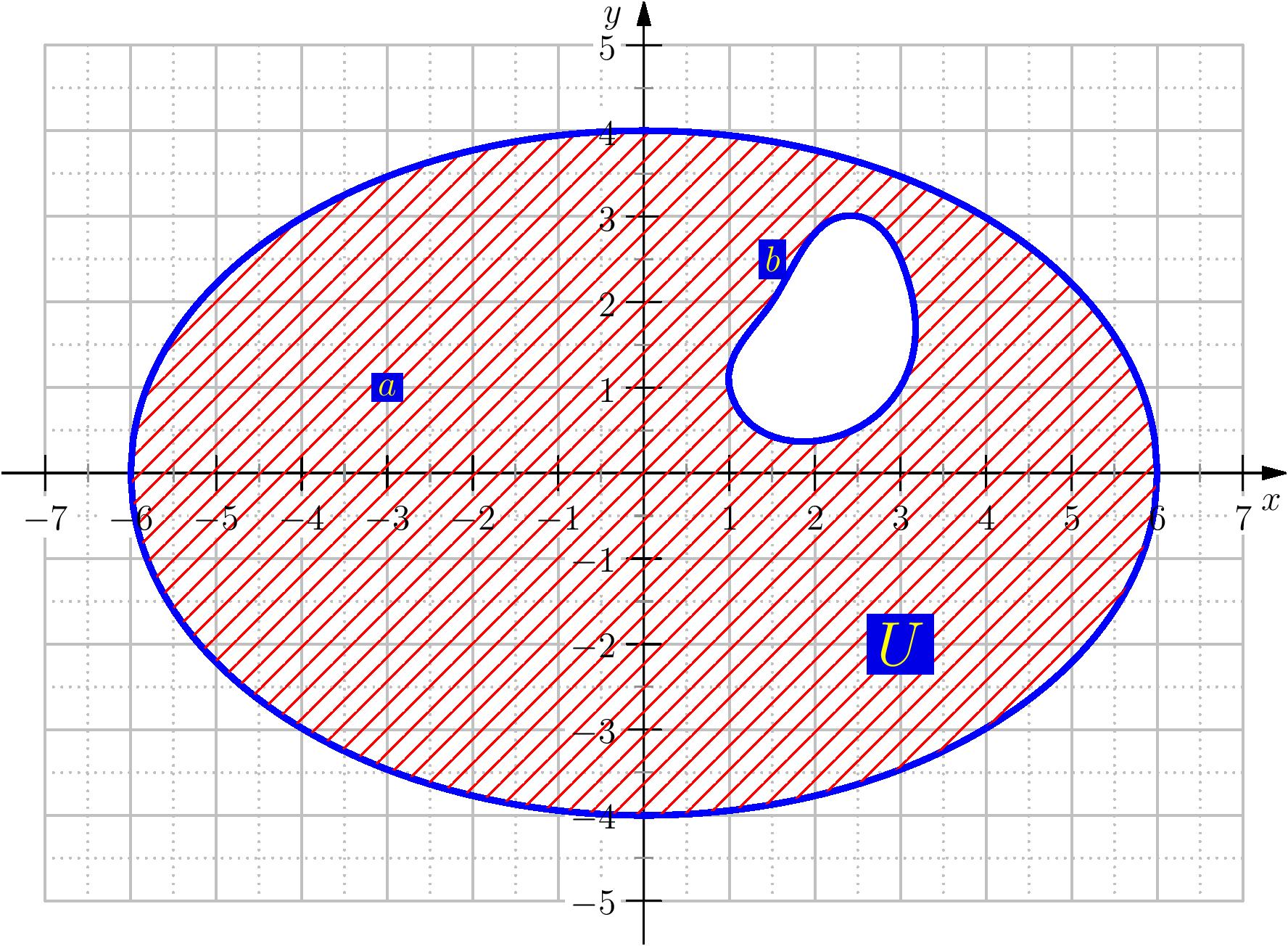
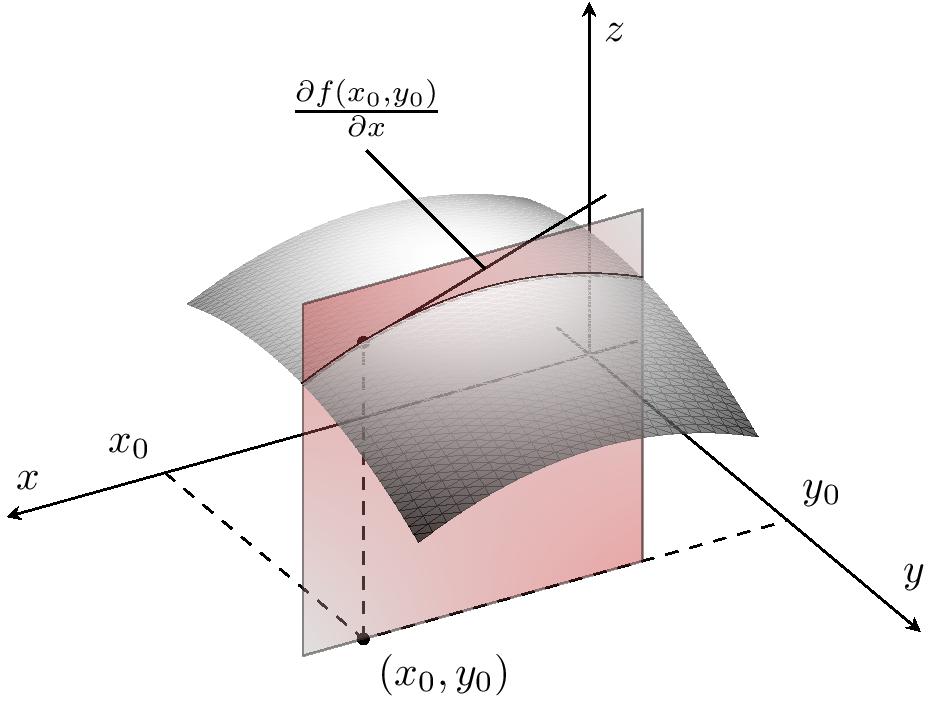
Soit $p\in \N^*$, on va étudier dans ce chapitre les applications de $\R^p$ dans $\R$ définies sur un ouvert
$U$ de $\R^p$.
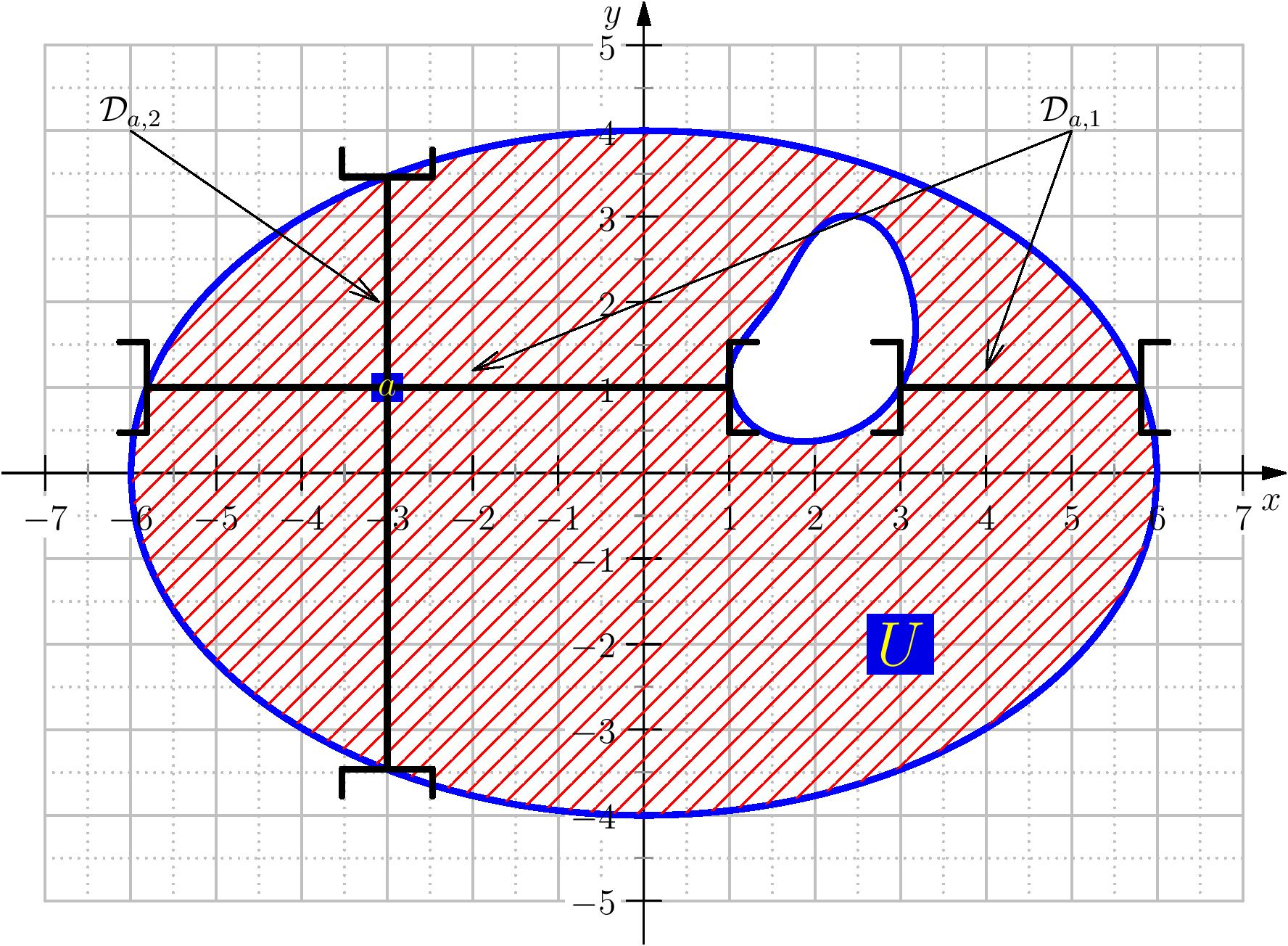
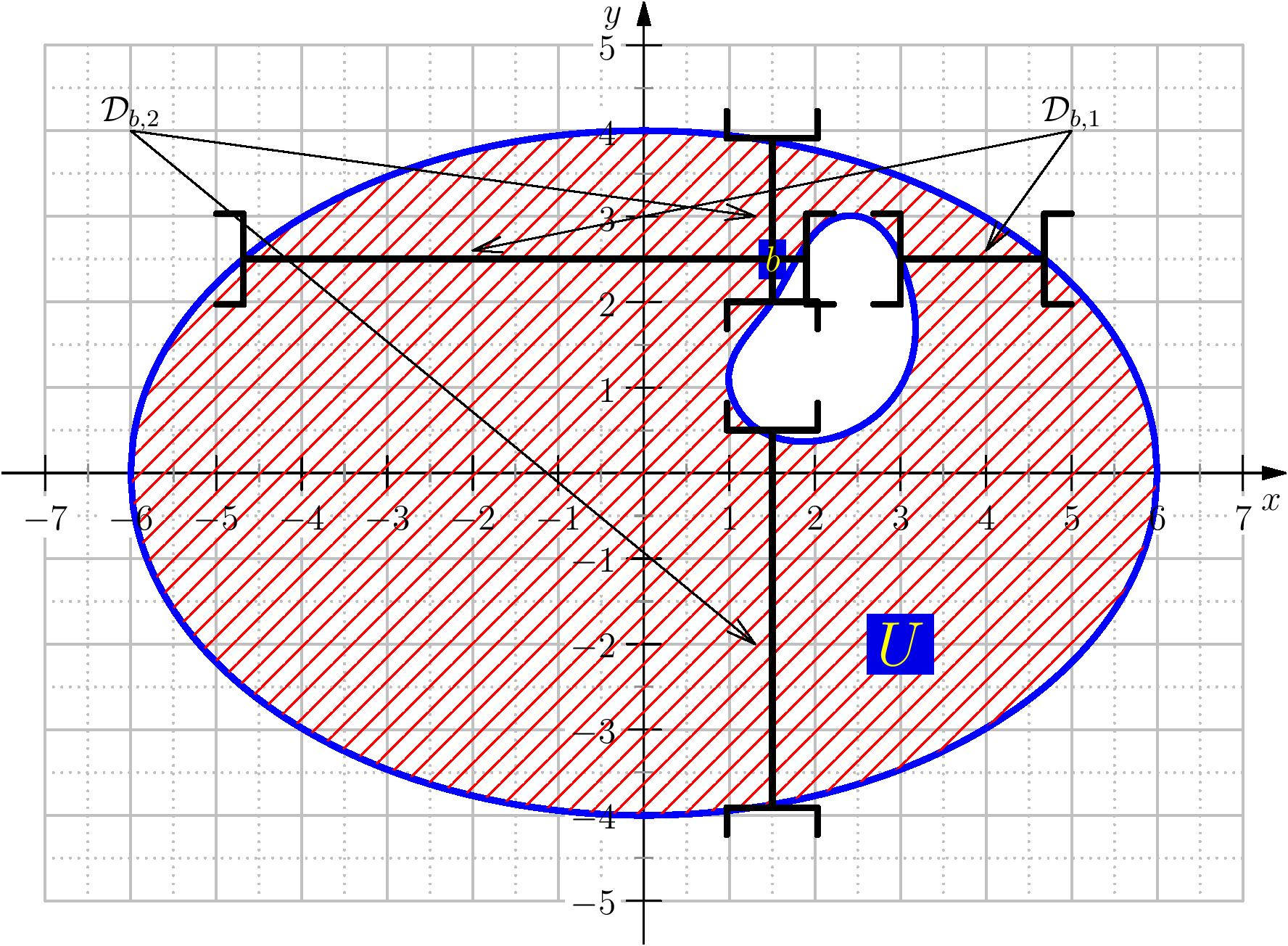
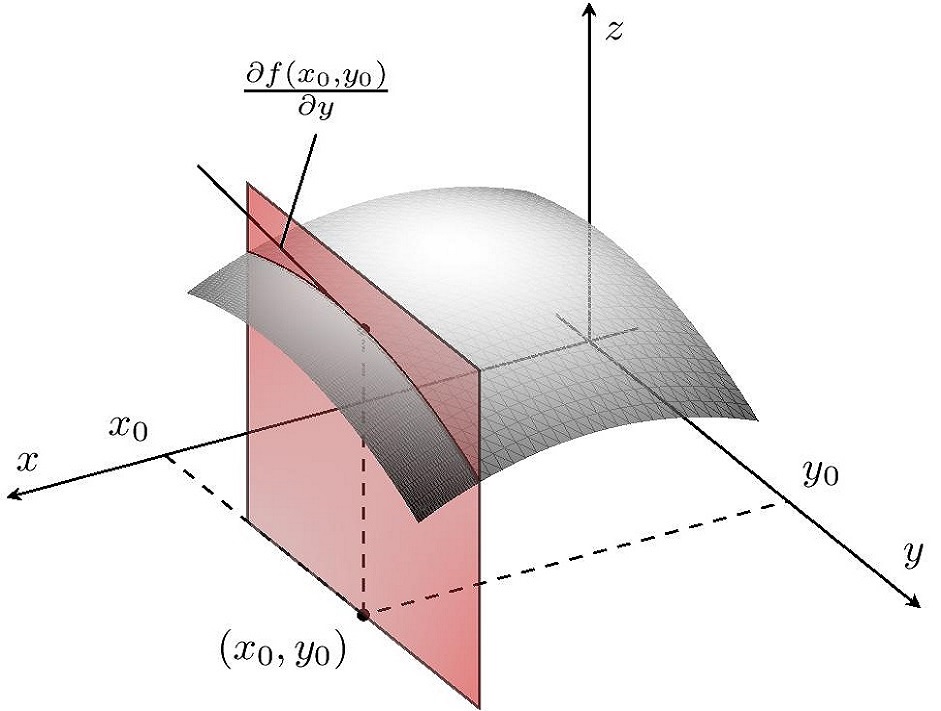
On note $\BB=(e_1,\cdots,e_p)$ la base canonique de $\R^p$. Pour
Comme $U$ est un ouvert alors, pour tout $i$, $D_{a,i}$ est un ouvert de $\R$.
Pour tout $a\in U$ et $i\in \inter{1,p}$, $f_{a,i}$ se définit aussi par: $$f_{a,i}(t)=f(a_1,\cdots,a_{i-1},t,a_{i+1},\cdots,a_p).$$
Soit $A\in \MM_n(\R)=(a_{i\,j})$. On considère, $$\fonct{f}{\R^n}{\R}{X}{{\,}^t X AX}$$ et $O={\,}^t (0,\cdots,0)$. Déterminer les fonctions partielles de $f$ en $O$.
Soit $k\in \inter{1,n}$, on a $D_{O,k}=\{t\in \R,\, O+(t-O_k)e_k\in \R^n\}=\R$ et $f_{O,k}(t)=f(te_k)=(t^2)
{\,}^t e_kAe_k$, or
$Ae_k$ donne $C_k$ la $k$ème colonne de $A$ et ${\,}^te_k C_k$ donne la $k$ème
coefficient de $C_k$.
On en déduit alors,
$$f_{O,k}(t)=a_{k\,k}t^2.$$
Dérivées partielles
| $\,$ |
Déterminer, pour chacune des fonctions suivantes, le domaine de définition $D_f$. Pour chacune des fonctions, calculer ensuite les dérivées partielles en chaque point du domaine de définition lorsqu'elles existent:
- $f(x,y)=x^2\ee^{xy}$,
- $f(x,y)=\ln(x+\sqrt{x^2+y^2})$,
- $f(x,y)=\sin^2 x+ \cos^2y$,
- $f(x,y,z)=x^2y^2\sqrt{z}$.
- $D_f=\R^2$. $$ \frac{\partial f}{\partial x}(x,y)= 2x\exp(xy)+x^2y\exp(xy),\quad \frac{\partial f}{\partial y}(x,y)= x^3\exp(xy).$$ \noindent
- $D_f=\{(x,y); x > 0 \ \text{ou} \ y \ne 0\}\subseteq \R^2$. $$\begin{array}{lcl} \frac{\partial f}{\partial x}(x,y)&=& \dsp\frac{1+\frac{x}{\sqrt{x^2+y^2}}}{x+\sqrt{x^2+y^2}}= \frac 1{\sqrt{x^2+y^2}},\quad\\ \frac{\partial f}{\partial y}(x,y)&=& \dsp \frac{\frac{y}{\sqrt{x^2+y^2}}}{x+\sqrt{x^2+y^2}} =\frac{y}{x\sqrt{x^2+y^2}+x^2+y^2}. \end{array}$$
- $D_f=\R^2$. $$ \frac{\partial f}{\partial x}(x,y)= 2\sin(x) \cos(x),\quad\frac{\partial f}{\partial y}(x,y)= -2\sin(y) \cos(y).$$
- $D_f=\{(x,y,z); z > 0\}\subseteq \R^3$. $$ \frac{\partial f}{\partial x}(x,y,z)= 2xy^2\sqrt{z},\quad \frac{\partial f}{\partial y}(x,y,z)= 2x^2y\sqrt{z} ,\quad \frac{\partial f}{\partial z}(x,y,z)= \frac {x^2y^2}{2\sqrt{z}} .$$
On note
Soit $\fonct{f}{\R^2}{\R}{(x,y)}{\Max (\abs{x},\abs{y})}$. Déterminer le plus grand ouvert de $\R^2$ sur le quel $f$ est de classe $\CC^1$.
Soit $\Delta_1\,:~~y=x$ et $\Delta_2\,:~~y=-x$. Notons $\Omega =\R^2\setminus (\Delta_1\cup \Delta_2)$.
$f$ est de classe $\CC^1$ sur $\Omega$ puisque la restriction de $f$ à $\Omega$ est:
$$(x,y)\longmapsto x\text{ ou } -x \text{ ou } y \text{ ou } -y.$$
Soit $x_0\in \R_+^*$, on a $f(x_0,x_0)=x_0$ et $f(x,x_0)=x$ pour $x>x_0$, et $f(x,x_0)=x_0$ pour $x\leq
x_0$. Ce qui donne:
$$\limiteX{x}{x_0^+}\dfrac{f(x,x_0)-f(x_0,x_0)}{x-x_0}=1,~~~~\limiteX{x}{x_0^-}\dfrac{f(x,x_0)-f(x_0,x_0)}{x-x_0}=0.$$
Donc $f$ n'admet pas de dérivée partielle par rapport à $x$ en $(x_0,x_0)$ donc $f$ n'est pas de classe
$\CC^1$ en $(x_0,x_0)$.
Le même raisonnement pour les autres cas montre que $f$ n'est pas de classe $\CC^1$ aux points de
$(\Delta_1\cup\Delta_2)$.
On en déduit que le plus grand ouvert de $\R^2$, sur le quel $f$ est de classe $\CC^1$ est $\Omega$.
- $fg\in \CC^1(U,\R)$, de plus pour tout $i\in \inter{1,p}$, on a: $$\dfrac{\partial \,(fg)}{\partial\,x_i}=f\dfrac{\partial \,g}{\partial\,x_i}+g\dfrac{\partial \,f}{\partial\,x_i}.$$
- Si $g$ ne s'annule pas sur $U$ alors $1/g\in \CC^1(U,\R)$ et on a: $$ \forall i\in \inter{1,p},\quad \dfrac{\partial}{\partial \,x_i}(\frac{1}{g})=\dfrac{-\dfrac{\partial\,g}{\partial \,x_i}}{g^2}.$$
Différentielle des fonctions de classe $\CC^1$
On dit alors que $f$ admet un DL à l'ordre 1 au voisinage de $a$.
Dans le théorème précédent, l'hypothèse $f\in \CC^1(U)$ est indispensable. En effet, $f$ peut admettre des dérivées partielles en $a$ sans que $\ud f(a)$ existe.
Soit $$ \fonct{f}{\R^2}{\R}{(x,y)}{\left\{\begin{array}{lcl} 0&\text{ si }& (x,y)=(0,0)\\ \dfrac{xy}{\sqrt{x^2+y^2}}&\text{ sinon }.& \end{array} \right.}$$ Montrer que $f$ admet des dérivées partielle en $(0,0)$. $f$ différentiable en $(0,0)$?
Clairement $f$ est continue en $(0,0)$, de plus $\dfrac{\partial f}{\partial x}(0,0)=\dfrac{\partial f}{\partial y}(0,0)=0$, donc si $f$ admet un différentielle en $(0,0)$, on aurai $\ud f_{(0,0)}=0$ et $$f(x,y)=f(0,0)+\ud f_{(0,0)}((x,y))+\underset{(x,y) \to (0,0)}{\mathrm{o}}(\norme{(x,y)})=\underset{(x,y)\to (0,0)}{\mathrm{o}}(\norme{(x,y)}).$$ Autrement dit, $\dfrac{f(x,y)}{\sqrt{x^2+y^2}}\tendvers{(x,y)}{(0,0)}\,0$, ce qui est absurde (par exemple $\dfrac{f(x,x)}{\sqrt{x^2+x^2}}=1/2$.)
Soit $f : \R^3 \to \R$ de classe $\CC^1$ telle que
$f(0,1,1) = 0$, $\frac{\partial f}{\partial x}(0,1,1) = 1$, $\frac{\partial f}{\partial y}(0,1,1) = 2$,
$\frac{\partial f}{\partial z}(0,1,1) = 3$.
Peut-on déterminer $\dsp\lim_{t\to 0} \frac{f(t^2,\ch t,\ee^t)}{f(t,\cos t,\ch t)}$ ?
Puisque $f$ est de classe $\CC^1$ alors $f$ admet un DL au voisinage de $(0,1,1)$, d'autre part, $$\ch(t)=1+\dfrac{t^2}{2}+\underset{t\to 0}{\mathrm{o}}(t^2),\, \cos(t)=1-\dfrac{t^2}{2}+\underset{t\to 0}{\mathrm{o}}(t^2),\,\ee^t=1+t+\dfrac{t^2}{2}+\underset{t\to 0}{\mathrm{o}}(t^2).$$ Ainsi, en posant $X=(t^2,\ch (t),\ee^t)=(0,1,1)+t(0,0,1)+\underset{t\to 0}{\mathrm{o}}(t)$ et $h=X-(0,1,1)$, $$\begin{array}{lcl} f(X)&=&\dsp f(0,1,1)+\frac{\partial f}{\partial x}(0,1,1)\times 0+\frac{\partial f}{\partial y}(0,1,1)\times 0+ \frac{\partial f}{\partial z}(0,1,1)\times 1+\underset{\norme{h}\to 0}{\mathrm{o}}(h)\\ &=&3t +\underset{\norme{h}\to 0}{\mathrm{o}}(h) \end{array} $$ On pose maintenant $Y=(t,\cos t,\ch t)=(0,1,1) +t(1,0,0)+\underset{t\to 0}{\mathrm{o}}(t)$ et $h=Y-(0,1,1)$, $$\begin{array}{lcl} f(Y)&=&\dsp f(0,1,1)+\frac{\partial f}{\partial x}(0,1,1)\times 1+\frac{\partial f}{\partial y}(0,1,1)\times 0+\frac{\partial f}{\partial z}(0,1,1)\times 0+\underset{\norme{h}\to 0}{\mathrm{o}}(h)\\ &=&t +\underset{\norme{h}\to 0}{\mathrm{o}}(h) \end{array} $$ On en déduit $$\lim_{t\to0} \frac{f(t^2,\ch t,\ee^t)}{f(t,\cos t,\ch t)}=\lim_{t\to0} \frac{3t +\underset{\norme{h}\to 0}{\mathrm{o}}(h)}{t +\underset{\norme{h}\to 0}{\mathrm{o}}(h)}=3.$$
L'existence de la différentielle de $f$ en $a$ assure uniquement l'existence des dérivées partielles de $f$ en $a$, i.e. $f$ n'est pas forcement de classe $\CC^1$ en $a$.
Considérons la fonction $f$ définie sur $\R^2$ par : $$f(0,0)=0 \text{ et pour }(x,y)\neq (0,0),\, f(x,y)=xy\sin\left(\dfrac{1}{\sqrt{x^2+y^2}} \right).$$ On a alors, pour tout $(x,y)\in \R^2$ $$\abs{f(x,y)-f(0,0)}\leq \abs{x}\abs{y}\leq \norme{(x,y)}^2.$$ Ceci montre que $f$ est continue en $(0,0)$ et de plus $f$ est différentiable en $(0,0)$ avec $\ud f_{(0,0)}=0$, ainsi $f$ admet des dérivées partielles en $(0,0)$ (elles sont nulles).
D'autre part, pour $(x,y)\neq (0,0)$, on a $$\frac{\partial f}{\partial x}(x,y)=y\sin\left(\dfrac{1}{\sqrt{x^2+y^2}} \right)- \dfrac{x^2y}{\sqrt{x^2+y^2}^3}\cos\left(\dfrac{1}{\sqrt{x^2+y^2}} \right)$$ Or celle-ci n'est pas continue en $(0,0)$. En effet, posons pour $n\in \N^*,\, u_n=\dfrac{1}{\pi\sqrt{2}n}(1,1)$, on a $u_n\tendversN\,(0,0)$ et $$ \dfrac{\partial f}{\partial x}(u_n)=\dfrac{1}{\pi\sqrt{2} n} \sin(\pi n)- \dfrac{1}{\sqrt{2}^3}\cos(\pi n ) =-\dfrac{(-1)^n}{2\sqrt{2}}\text{ ne tend pas vers }0$$
On définit $\fonct{\varphi}{\MM_n(\R)}{\R}{A}{\tr (A)}$. Montrer que $\varphi$ est de classe $\CC^1$ sur $\MM_n(\R)$ puis déterminer les dérivées partielles de $\varphi$.
On sait que $\varphi$ est continue (une application linéaire sue un espace vectoriel de dimension
finie).
Soit $A,H\in \MM_n(\R)$, on a
$$\varphi(A+H)=\tr (A+H)=\tr (A)+\tr (H)=\varphi(A)+\varphi(H).$$
En utilisant le résultat du théorème précédent, et en posant $\ell_A=\varphi$, on trouve que
$\varphi$ admet des dérivées partielles. Si on note $\BB =(E_i)_{i\in \inter{1,n^2}}$ la base canonique de
$\MM_n(\R)$, on a $\dfrac{\partial \varphi}{\partial E_k}(A)=\tr (E_k)$. Comme les
fonctions $\dfrac{\partial \varphi}{\partial E_k}$ sont continues sur $\MM_n(\R)$,
on en déduit que $\varphi\in \CC^1(\MM_n(\R))$.
$\varphi$ est
de classe $\CC^1$
sur $\MM_n(\R)$.
Par exemple, si $n=2$ et en notant $$E_1=\begin{pmatrix} 1&0\\0&0 \end{pmatrix},\,E_2=\begin{pmatrix} 0&1\\0&0 \end{pmatrix},\,\,E_3=\begin{pmatrix} 0&0\\1&0 \end{pmatrix},\,\,E_4=\begin{pmatrix} 0&0\\0&1 \end{pmatrix}$$ Alors, $\dfrac{\partial \varphi}{\partial E_1}(A)=\dfrac{\partial \varphi}{\partial E_4}(A)=1$, et $\dfrac{\partial \varphi}{\partial E_2}(A)=\dfrac{\partial \varphi}{\partial E_3}(A)=0$.
On définit $\fonct{\varphi}{\MM_n(\R)}{\R}{A}{\tr (A^2)}$. Montrer que $\varphi$ est de classe $\CC^1$ sur $\MM_n(\R)$ puis déterminer les dérivées partielles de $\varphi$.
Soit $A,H\in \MM_n(\R)$, on a $$\varphi(A+H)=\tr ((A+H)^2)=\tr (A^2+AH+HA+H^2)=\varphi(A)+\tr(AH+HA)+\tr(H^2).$$ Comme la fonction $\tr$ est continue, alors $\abs{\tr(H^2)}\leq K \norme{H^2}\leq K\norme{H}^2$ (avec $K>0$), donc $\tr(H^2)=\mathrm{o}(h)$.
En utilisant le résultat du théorème précédent, et en posant $\ell_A(H)=\tr (AH+HA)$, on trouve que $\varphi$ est de classe $\CC^1$ sur $\MM_n(\R)$. En effet, si on note $\BB =(E_i)_{i\in \inter{1,n^2}}$ la base canonique de $\MM_n(\R)$, on a $\dfrac{\partial \varphi}{\partial E_k}(A)=\tr (AE_k+E_kA)$ et $A\mapsto \tr (AE_k+E_kA)$ est continue sur $\MM_n(\R)$.
Par exemple, si $n=2$ et en notant $$E_1=\begin{pmatrix} 1&0\\0&0 \end{pmatrix},\,E_2=\begin{pmatrix} 0&1\\0&0 \end{pmatrix},\,\,E_3=\begin{pmatrix} 0&0\\1&0 \end{pmatrix},\,\,E_4=\begin{pmatrix} 0&0\\0&1 \end{pmatrix},\,\,A=\begin{pmatrix} x&y\\ z&w \end{pmatrix}$$ Alors, $$\dfrac{\partial \varphi}{\partial E_1}(A)=\tr (\begin{pmatrix} x&y\\ z&w \end{pmatrix}\begin{pmatrix} 1&0\\0&0 \end{pmatrix}+\begin{pmatrix} 1&0\\0&0 \end{pmatrix}\begin{pmatrix} x&y\\ z&w \end{pmatrix}) =\tr (\begin{pmatrix} x+x&y\\ z&0 \end{pmatrix})=2x$$ et $\dfrac{\partial \varphi}{\partial E_2}(A)=2z,\,\dfrac{\partial \varphi}{\partial E_3}(A)=2y,\,\,\dfrac{\partial \varphi}{\partial E_4}(A)=2w$.
- $\ud (\lambda f+g)(a)=\lambda \ud f(a)+\ud g(a)$.
- $\ud (fg)(a)=g(a)\ud f(a)+f(a)\ud g(a)$.
- Si $g(a)\neq 0$ alors $\ud\left(\frac{1}{g}\right)(a)=\frac{-1}{g(a)^2}\ud g(a)$.
Gradient
Soit $f:\R^p\longmapsto \R$ définie par $f(x)=\norme{x}$. Montrer que $f$ est de classe $\CC^1$ sur $\R^p\setminus\{0\}$, et déterminer, pour $x\neq 0$, $\nabla f(x)$.
Il suffit d'écrire, pour $x\neq 0$, $$\begin{array}{lcl} f(x+h)&=&\dsp\norme{x}\left(1+2\frac{\scal{x}{h}}{\norme{x}^2}+\dfrac{\norme{h}^2}{\norme{x}^2}\right)^{\frac{1}{2}}\\ &=&\dsp f(x)+\frac{\scal{x}{h}}{\norme{x}}+\mathrm{o}(h)=f(x)+ \scal{\frac{x}{\norme{x}}}{h}+\mathrm{o}(h). \end{array}$$ On en déduit que, pour $x\neq 0$, $\nabla f(x)=\dfrac{x}{\norme{x}}$.
Composition des fonctions de classe $\CC^1$
Alors
Soient $f\in \CC^1(U,\R)$ et $v\in \R^p\setminus\{0\}$. On pose $g(t)=f(a+tv)$ ($a\in U$ et $t\in \R$ tel
que $a+tv\in U$).
Calculer $g'$.
On note $v=(v_1,\cdots,v_p)$ et $\Phi(t)=a+tv$ (pour $t\in \R,$ t.q. $a+tv\in I$), alors on a $\Phi'(t)=v$, puis en appliquant la règle de la chaîne, on obtient, $$g'(t)=\ud f (\Phi(t))\cdot \Phi'(t)=\dsum_{j=1}^pv_j\partial_j f(a+tv).$$
Alors
Soit $f\in \CC^1(\R^2,\R)$, on définit $g:\R^2\longmapsto \R$ par, $$\forall (r,\theta)\in \R^2,\quad g(r,\theta)=f(r\cos(\theta),r\sin(\theta)).$$ Montrer que $g$ est de classe $\CC^1$ sur $\R^2$ puis calculer ses dérivées partielles, en déduire $\nabla f(x,y)$ en fonction des dérivées de $g$ pour $(x,y)=(r\cos(\theta),r\sin(\theta))\neq (0,0)$.
Avec les notations ci-dessus, on a $$ \dfrac{\partial g(r,\theta)}{\partial r}= \dfrac{\partial f}{\partial x}\dfrac{\partial x}{\partial r}+ \dfrac{\partial f}{\partial y}\dfrac{\partial y}{\partial r} =\cos (\theta)\dfrac{\partial f}{\partial x}+\sin(\theta)\dfrac{\partial f}{\partial y} $$ et, $$ \dfrac{\partial g(r,\theta)}{\partial \theta}= \dfrac{\partial f}{\partial x}\dfrac{\partial x}{\partial \theta}+ \dfrac{\partial f}{\partial y}\dfrac{\partial y}{\partial \theta}0 =-r\sin (\theta)\dfrac{\partial f}{\partial x}+r\cos(\theta)\dfrac{\partial f}{\partial y} $$ En multipliant la 1ère relation par $r\cos(\theta)$ et la deuxième par $-\sin(\theta)$, on trouve $$r\cos(\theta)\dfrac{\partial g(r,\theta)}{\partial r}-\sin(\theta) \dfrac{\partial g(r,\theta)}{\partial \theta} = r\cos^2(\theta)\dfrac{\partial f}{\partial x}+r\sin^2(\theta)\dfrac{\partial f}{\partial x} = r\dfrac{\partial f}{\partial x}$$ En multipliant la 1\up{ère} relation par $r\sin(\theta)$ et la deuxième par $\cos(\theta)$, on trouve $$r\sin(\theta)\dfrac{\partial g(r,\theta)}{\partial r}+\cos(\theta) \dfrac{\partial g(r,\theta)}{\partial \theta} = r\sin^2(\theta) \dfrac{\partial f}{\partial y}+r\cos^2(\theta)\dfrac{\partial f}{\partial x} = r\dfrac{\partial f}{\partial y}$$ Comme $r\neq 0$, on peut alors écrire $$\dfrac{\partial f}{\partial x}=\cos(\theta)\dfrac{\partial g}{\partial r}-\frac{\sin(\theta)}{r}\dfrac{\partial g}{\partial \theta},\,\, \dfrac{\partial f}{\partial y}=\sin(\theta)\dfrac{\partial g}{\partial r}+\frac{\cos(\theta)}{r}\dfrac{\partial g}{\partial \theta}.$$ Souvent, en physique, on note $\vec{u}_r=\cos(\theta)\vec{i}+\sin(\theta)\vec{j}$, et $ \vec{u}_\theta=-\sin(\theta)\vec{i}+\cos(\theta)\vec{j}$, ce qui donne, $$ \nabla f (x,y)=\dfrac{\partial g}{\partial r}(r,\theta)\vec{u}_r+\dfrac{1}{r}\dfrac{\partial g}{\partial \theta}(r,\theta) \vec{u}_\theta.$$
Dérivées partielles d'ordre deux
Attention à l'ordre, $\dfrac{\partial^2 f}{\partial x_k\,\partial x_j}(a)$ n'est pas forcément égale à $\dfrac{\partial^2 f}{\partial x_j\,\partial x_k}(a)$!
Soit $f$ et $\varphi :\mathbb{R} \to \mathbb{R}$ deux applications de classe $\CC^2 $ et $F:\mathbb{R}^2 \to \mathbb{R}$ définie par $F(x,y) = f(x + \varphi (y))$
- Justifier que $F$ est de classe $\CC^2 $.
- Vérifier l'égalité : $\dfrac{{\partial ^2 F}}{{\partial x^2 }}\dfrac{{\partial F}}{{\partial y}} - \dfrac{{\partial ^2 F}}{{\partial x\partial y}}\dfrac{{\partial F}}{{\partial x}} = 0$.
Il est claire que $F$ est de classe $\CC^1$ sur $\R^2$ comme la somme et la composée des fonctions de
classes $\CC^1$.
Soit $(x,y)\in \R^2$, on a
$$\dfrac{\partial F}{\partial x}(x,y)=f'(x+\varphi(y)),\quad \dfrac{\partial F}{\partial
y}(x,y)=f'(x+\varphi(y))\varphi'(y).$$
Les deux dérivées partielles de $F$ sont également de classe $\CC^1$ (puisque $f,\varphi\in \CC^2$, donc
$f',\varphi'\in \CC^1(\R)$, et on a:
$$\begin{array}{lcl}
\dsp\dfrac{\partial^2 F}{\partial x^2}(x,y)&=&\dsp\dfrac{\partial }{\partial
x}(f'(x+\varphi(y)))=f''(x+\varphi(y))\\
\dsp\dfrac{\partial^2 F}{\partial y\partial x}(x,y)&=&\dsp\dfrac{\partial }{\partial
y}(f'(x+\varphi(y)))=f''(x+\varphi(y))\varphi'(y)\\
\dsp\dfrac{\partial^2 F}{\partial x\partial y}(x,y)&=&\dsp\dfrac{\partial }{\partial
x}(f'(x+\varphi(y))\varphi'(y))=f''(x+\varphi(y))\varphi'(y)\\
\dsp\dfrac{\partial^2 F}{\partial y^2}(x,y)&=&\dsp\dfrac{\partial }{\partial
y}(f'(x+\varphi(y))\varphi'(y))=f''(x+\varphi(y))\varphi'(y)^2+f'(x+\varphi(y))\varphi''(y)
\end{array}
$$
Les quatres fonctions ci-dessus sont continues sur $\R^2$, on en déduit alors que $F\in
\CC^2(\R^2,\R)$.
Soit $(x,y)\in \R^2$, on a
$$\begin{array}{lcl}
\dfrac{{\partial ^2 F}}{{\partial x^2 }}\dfrac{{\partial F}}{{\partial y}} - \dfrac{{\partial ^2
F}}{{\partial x\partial y}}\dfrac{{\partial F}}{{\partial x}}
&=&f''(x+\varphi(y))f'(x+\varphi(y))\varphi'(y)-f''(x+\varphi(y))\varphi'(y)f'(x+\varphi(y))\\
\end{array}
$$
On suppose que $\dfrac{\partial^2 f}{\partial x_j\,\partial x_k}$ et $\dfrac{\partial^2 f}{\partial
x_k\,\partial x_j}$ existent sur $U$.
Si ces fonctions sont continues en $a\in U$, alors:
Soit $f:\R^2\longmapsto\R$ définie par, $$f(0,0)=0,\quad f(x,y)=\dfrac{xy(x^2-y^2)}{x^2+y^2},\text{ pour } (x,y)\neq (0,0).$$ Montrer que $ \dfrac{\partial^2 f}{\partial y\,\partial x}(0,0)$ et $ \dfrac{\partial^2 f}{\partial x\,\partial y}(0,0)$ existent et les calculer.
Après calculs, on trouve: $$\dfrac{\partial f}{\partial\,x}(x,y)=\left\{\begin{array}{lcl} \dfrac{x^4y+4x^2y^3-y^5}{(x^2+y^2)^2}&\text{ si }& (x,y)\neq (0,0)\\ 0&\text{sinon} \end{array} \right. $$ $$\dfrac{\partial f}{\partial\,y}(x,y)=\left\{\begin{array}{lcl} \dfrac{-xy^4-4x^3y^2+x^5}{(x^2+y^2)^2}&\text{ si }& (x,y)\neq (0,0)\\ 0&\text{sinon} \end{array} \right. $$ Puis, $$ \dfrac{\partial^2 f}{\partial y\partial\,x}(0,0)=\limiteX{y}{0}\frac{1}{y}\left(\dfrac{\partial f}{\partial\,x}(0,y)-\dfrac{\partial f}{\partial\,x}(0,0)\right)=-1. $$ $$ \dfrac{\partial^2 f}{\partial x\partial\,y}(0,0)=\limiteX{x}{0}\frac{1}{x}\left(\dfrac{\partial f}{\partial\,y}(x,0)-\dfrac{\partial f}{\partial\,y}(0,0)\right)=1. $$
Il est clair que la matrice $H_f(a)$ est symétrique (d'après le thm de Schwarz) à coefficients réelles, donc $H(a)$ est diagonalisable dans $\MM_n(\R)$.
Soit $f\in \CC^2(U,\R)$. Pour tout $a\in U$. Alors, pour tout $h\in \R^p$ tel que $a+h\in U$, on a
Si on pose $h=(h_1,\cdots,h_p)^\top$, alors: $$f(a+h)=f(a)+\dsum_{k=1}^ph_k\dfrac{\partial f}{\partial x_k}(a)+\dfrac{1}{2}\dsum_{1\leq i,j\leq p}h_ih_j\dfrac{\partial^2 f}{\partial x_i\partial x_j}(a) + \underset{\norme{h}\to 0}{\mathrm{o}}(\norme{h}^2)$$
- Si $f,g\in \CC^2(U,\R)$ alors $fg\in \CC^2(U,\R)$.
- Si $f$ ne s'annule pas sur $U$ alors $\frac{1}{f}\in \CC^2(U,\R)$.
Trouver les applications $\varphi\in \CC^3(\R_+^*,\R)$ telles que l'application $\fonct{f}{\R^3\setminus\{(0,0,0)\}}{\R}{(x,y,z)}{\varphi(x^2+y^2+z^2)}$, vérifie: $$\forall (x,y,z)\in \R^3\setminus\{(0,0,0)\},\quad\,\dfrac{\partial^3\,f}{\partial\,x\partial\,y\partial\,z}(x,y,z)=\dfrac{xyz}{x^2+y^2+z^2}.$$
Soit $\varphi\in \CC^3(\R_+^*,\R)$. On définit
$\fonct{f}{\R^3\setminus\{0\}}{\R}{(x,y,z)}{\varphi(x^2+y^2+z^2)}$, $f$ est de classe $\CC^3$ sur
$\R^3\setminus\{0\}$ (composition des fonctions de classe $\CC^3$).
En dérivant $f$, on trouve:
$$\forall (x,y,z)\neq (0,0,0),~~\dfrac{\partial
^3f}{\partial\,x\partial\,y\partial\,z}(x,y,z)=8xyz\varphi^{(3)}(x^2+y^2+z^2).$$
Ainsi, $f$ vérifie la relation de l'énoncé ssi $\varphi$ vérifie:
$$\forall t\in \R_+^*,~~\varphi^{(3)}(t)=\dfrac{1}{8t}.$$
En intégrant, on trouve:
$$\forall t>0,~~\varphi(t)=\dfrac{1}{16}t^2\ln(t)+At^2+Bt+c,~~~~A,B,C\in \R.$$
On considère l'équation aux dérivées partielles : $$\dfrac{\partial f}{\partial u}(u,v)+2u\dfrac{\partial f}{\partial v}(u,v)=0 \quad(\EE)$$
- Montrer que l'application $\varphi: (x,y) \mapsto (x,y+x^2)$ est bijective de $\R^2$ sur $\R^2$ et que $\varphi$ et son inverse sont de classe $\CC^1$.
- À l'aide d'un changement de fonction inconnue, déterminer toutes les solutions de $(\EE)$ de classe $\CC^1$ sur $\R^2$.
- Il est clair que $\varphi$ est bijective donc la fonction inverse est $\fonct{\varphi^{-1}}{\R^2}{\R^2}{(u,v)}{(u,v-u^2)}$. De plus $\varphi$ et $\varphi^{-1}$ sont des fonctions de classe $\CC^1$ sur $\R^2$ (fonctions polynomiales par rapport au coordonnées).
-
On pose $f^*(x,y)=f(\varphi(x,y))$.
$$\dfrac{\partial f^*}{\partial\,x}=\dfrac{\partial f}{\partial\,u}\dfrac{\partial
u}{\partial\,x}+\dfrac{\partial f}{\partial\,v}\dfrac{\partial v}{\partial\,x}=\dfrac{\partial
f}{\partial\,u}+2u\dfrac{\partial f}{\partial\,v}.$$
Ainsi, si $f$ est une solution de $(\EE)$ alors $f^*$ vérifie $\dfrac{\partial f^*}{\partial\,x}=0$.
En intégrant cette équation on trouve $f^*(x,y)=g(y)$ ou $g\in \CC^1(\R)$.
On en déduit que l'ensemble de solution de $(\EE)$ est $\{(u,v)\longmapsto g(v-u^2),~~g\in \CC^1(\R,\R)\}$.
On note $U=\{(x,y)\in \R^2,\,y>\abs{x}\}$. Trouver les applications $f\in \CC^2(U,\R)$ telles que: $$\forall (x,y)\in U,~~\dfrac{\partial^2\,f}{\partial\,x^2}(x,y)-\dfrac{\partial^2\,f}{\partial\,y^2}(x,y)=\dfrac{1}{\sqrt{y^2-x^2}}.$$ En utilisant le changement de variable $u=x+y$ et $v=y-x$.
Considérons l'application $\fonct{\varphi}{U}{\R^2}{(x,y)}{(x+y,y-x)}$, d'après la définition de $U$, on a
$\varphi(U)=V=(\R_+^*)^2$.
Il est clair que $\varphi$ est $\CC^2$- difféomorphisme de $U$ sur $V$.
Soit $f\in \CC^2(U,\R)$, on définit $F\in \CC^2(V,\R)$ telle que $f(x,y)=F(u,v)$. On a
$$\left\{\begin{array}{lclcl}
\dfrac{\partial f}{\partial\,x}&=&
\dfrac{\partial F}{\partial\,u}\dfrac{\partial u}{\partial\,x}+\dfrac{\partial
F}{\partial\,v}\dfrac{\partial v}{\partial\,x}&=&\dfrac{\partial F}{\partial\,u}-\dfrac{\partial
F}{\partial\,v}.\\
&&&&\\
\dfrac{\partial f}{\partial\,y}&=&
\dfrac{\partial F}{\partial\,u}\dfrac{\partial u}{\partial\,y}+\dfrac{\partial
F}{\partial\,v}\dfrac{\partial v}{\partial\,y}&=&\dfrac{\partial F}{\partial\,u}+\dfrac{\partial
F}{\partial\,v}.
\end{array}
\right.$$
Ensuite, on calcul les dérivées partielles d'ordre 2 (on utilise aussi le théorème de Schwarz):
$$
\left\{\begin{array}{lclcl}
\dfrac{\partial^2 f}{\partial\,x^2}&=&
\dfrac{\partial^2 F}{\partial\,u^2}-\dfrac{\partial^2 F}{\partial v\,\partial\,u}-\dfrac{\partial^2
F}{\partial \,v\partial\,u}+\dfrac{\partial^2 F}{\partial\,v^2}&=&\dfrac{\partial^2
F}{\partial\,u^2}-2\dfrac{\partial^2 F}{\partial\,u\partial\,v}+\dfrac{\partial^2 F}{\partial\,v^2}\\
&&&&\\
\dfrac{\partial^2 f}{\partial\,y^2}&=&
\dfrac{\partial^2 F}{\partial\,u^2}+\dfrac{\partial^2 F}{\partial v\,\partial\,u}+\dfrac{\partial^2
F}{\partial \,v\partial\,u}+\dfrac{\partial^2 F}{\partial\,v^2}&=&\dfrac{\partial^2
F}{\partial\,u^2}+2\dfrac{\partial^2 F}{\partial\,u\partial\,v}+\dfrac{\partial^2 F}{\partial\,v^2}
\end{array}
\right.
$$
Ainsi, si $f$ est une solution de l'équation, on trouve que $F$ vérifie l'équation suivante:
$$\forall (u,v)\in V,~~~~-4\dfrac{\partial^2 F}{\partial\,u\partial\,v}=\dfrac{1}{\sqrt{uv}}.$$
En intégrant cette dernière équation par rapport à $u$ ($v$ est fixe), on trouve:
$$\forall (u,v)\in V,~~~~\dfrac{\partial
F}{\partial\,v}=\dfrac{-1}{2}\dfrac{\sqrt{u}}{\sqrt{v}}+h(v),~~h\in \CC^1(\R_+^*,\R).$$
On intègre à nouveau par rapport à $v$, on obtient,
$$\forall (u,v)\in V,~~F(u,v)=-\sqrt{uv}+H(v)+L(u),~~H,L\in \CC^2(\R_+^*,\R).$$
On en déduit l'ensemble de solutions de l'EDP est:
$$\boxed{\left\{(x,y)\in U\longmapsto -\sqrt{y^2-x^2}+A(x+y)+B(y-x),~~~~A,B\in
\CC^2(\R_+^*,\R)\right\}}.$$
Applications géométriques
Courbes planes d'équation $F(x,y)=0$
Comment peut-on définir une courbe? ou tout simplement que veut dire courbe dans le plan ou dans
l'espace?
En réalité, une courbe dans l'espace de dimension $d$ est un objet qui peut être
décrit par un point qui évolue au cours du temps (en physique on parle d'un point matériel soumis à
certaines
forces).
Autrement dit, il suffit d'un paramètre
pour le décrire, le temps. On dit d'un tel objet qu'il est 1-dimensionnel (variété de dimension 1).
Prenons l'exemple d'un point matériel 'notre planète terre'. Au cours du temps la terre soumis à la force de
gravité du soleil
(mais aussi d'autre objets!) décrit une trajectoire, une courbe dans l'espace.
Nous avons déjà vu qu'on peut définir une courbe dans le plan par l'ensemble des points $M(x,y)$ tels que
$y=f(x)$ avec $f$ une
fonction de $I$ dans $\R$, mais également les courbes définies par un arc paramétrée $\Gamma
=(x(t),y(t))$.
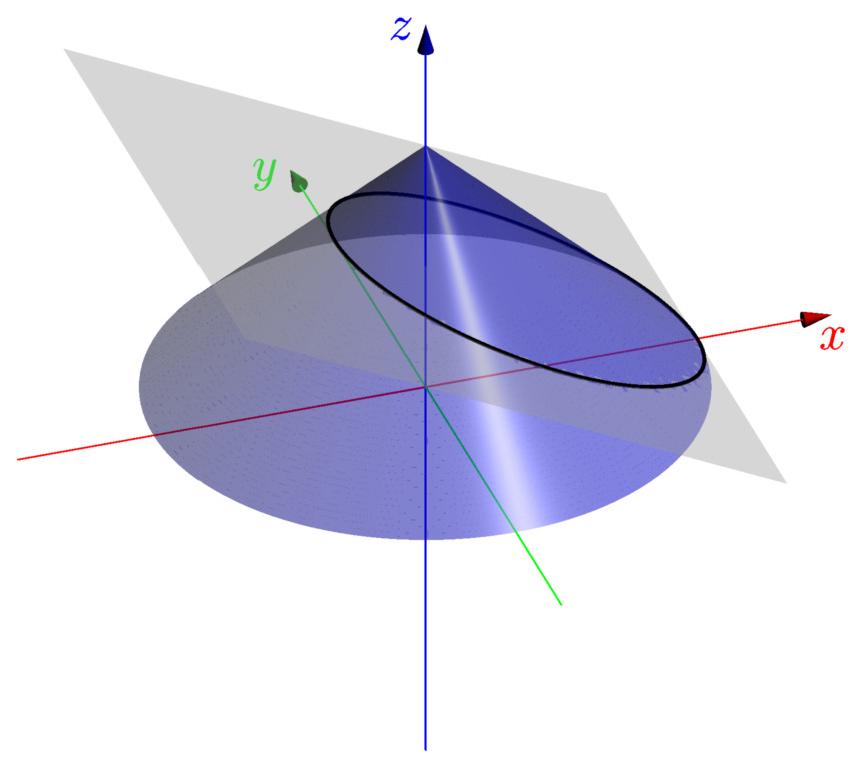
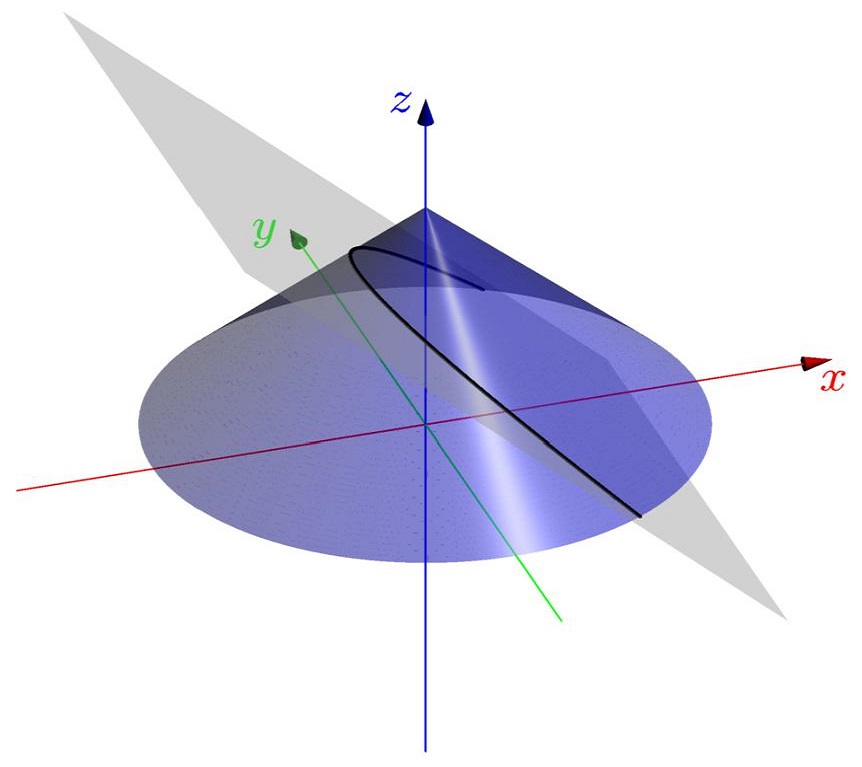
On peut également obtenir une courbe en faisant l'intersection entre une surface (dans l'espace) et un plan,
ci-après les
exemples classique d'intersection d'un cône avec un plan.
| $\,$ |
|
|
| L'intersection est une ellipse | $\,$ | L'intersection une partie d'hyperbole |
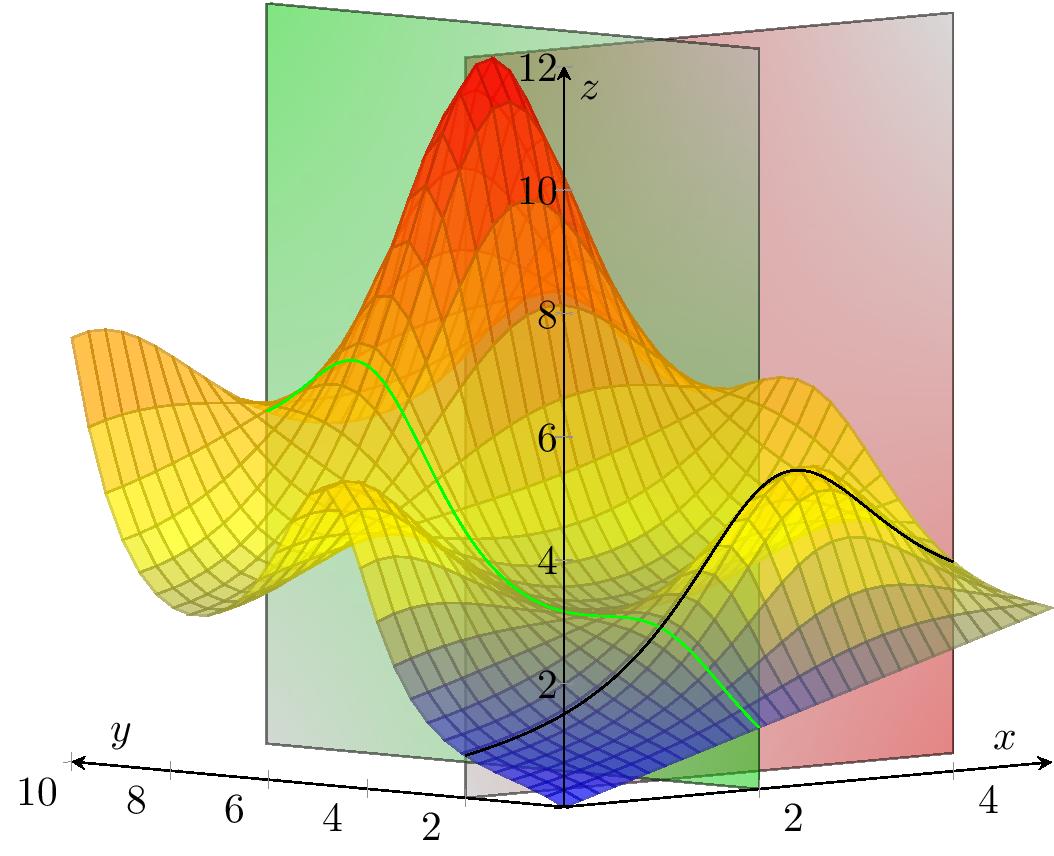
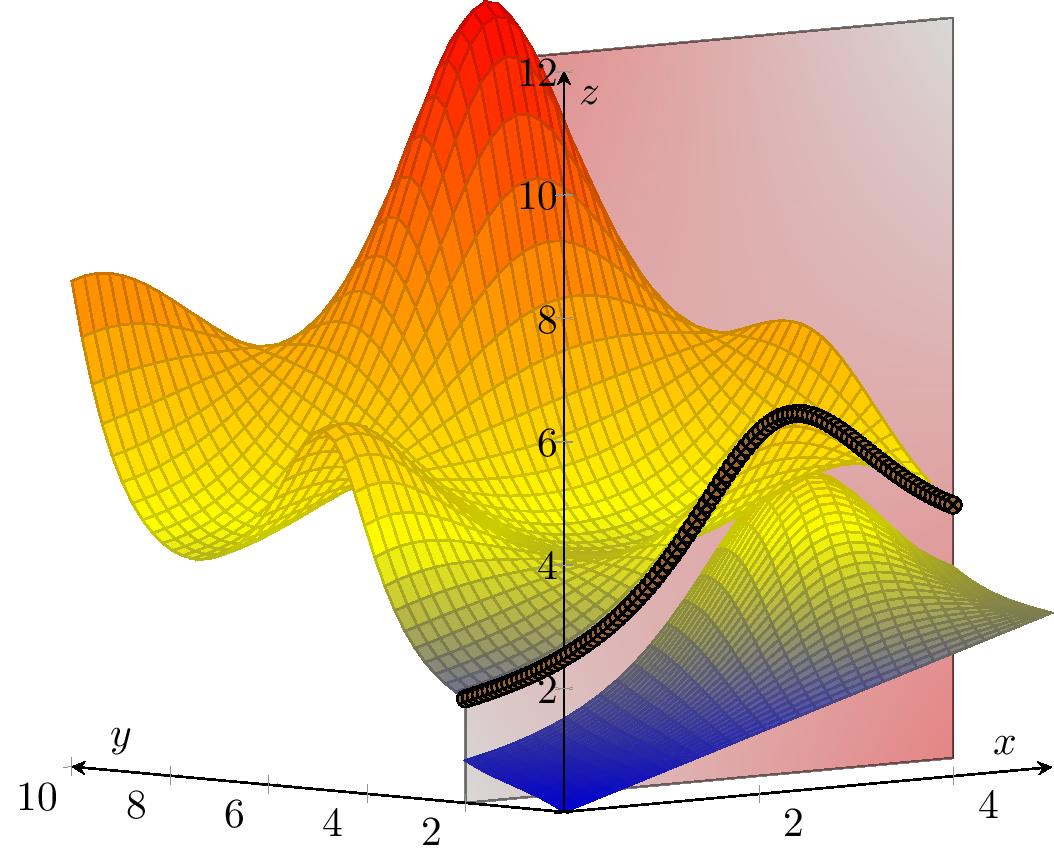
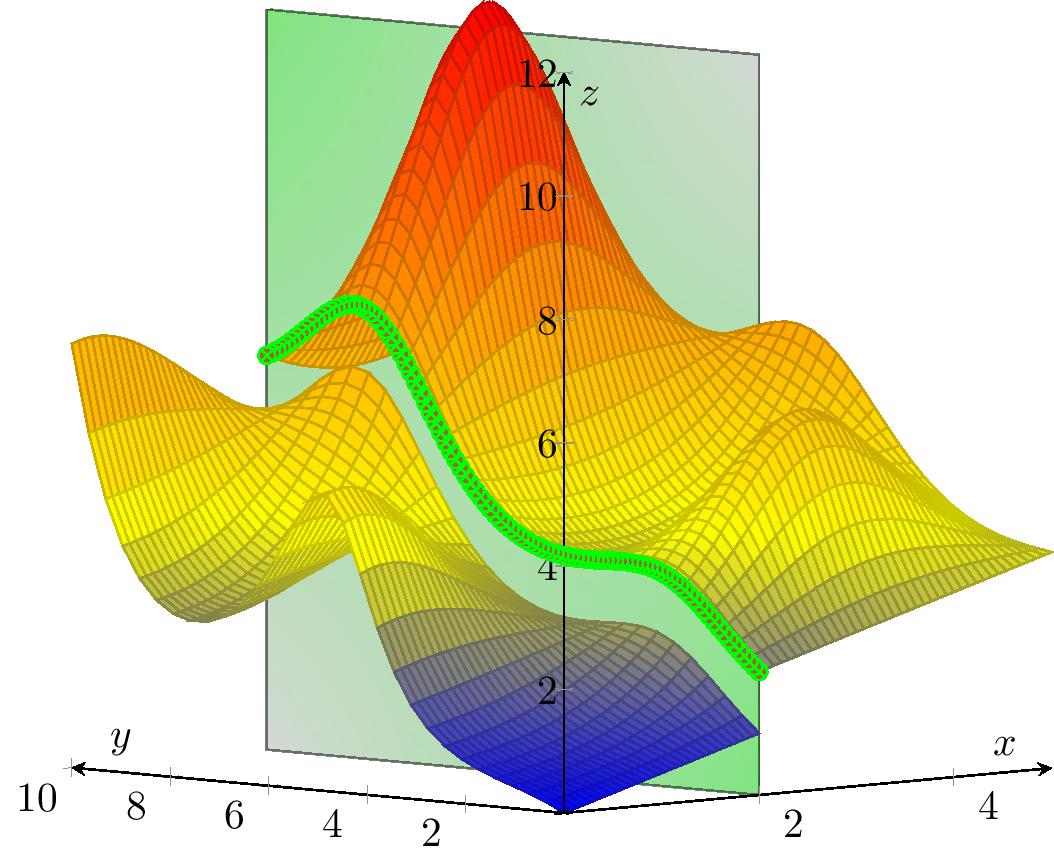
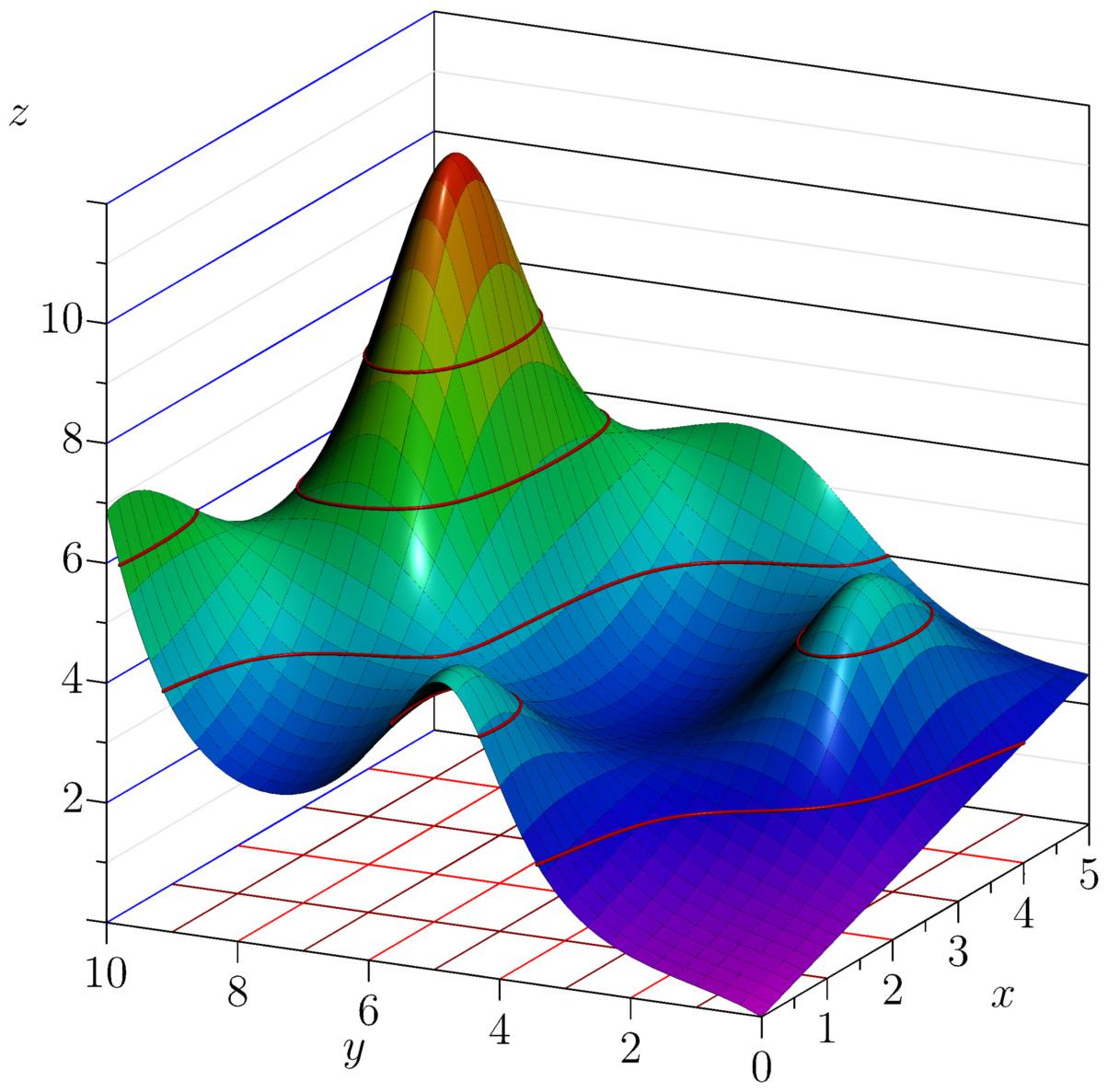
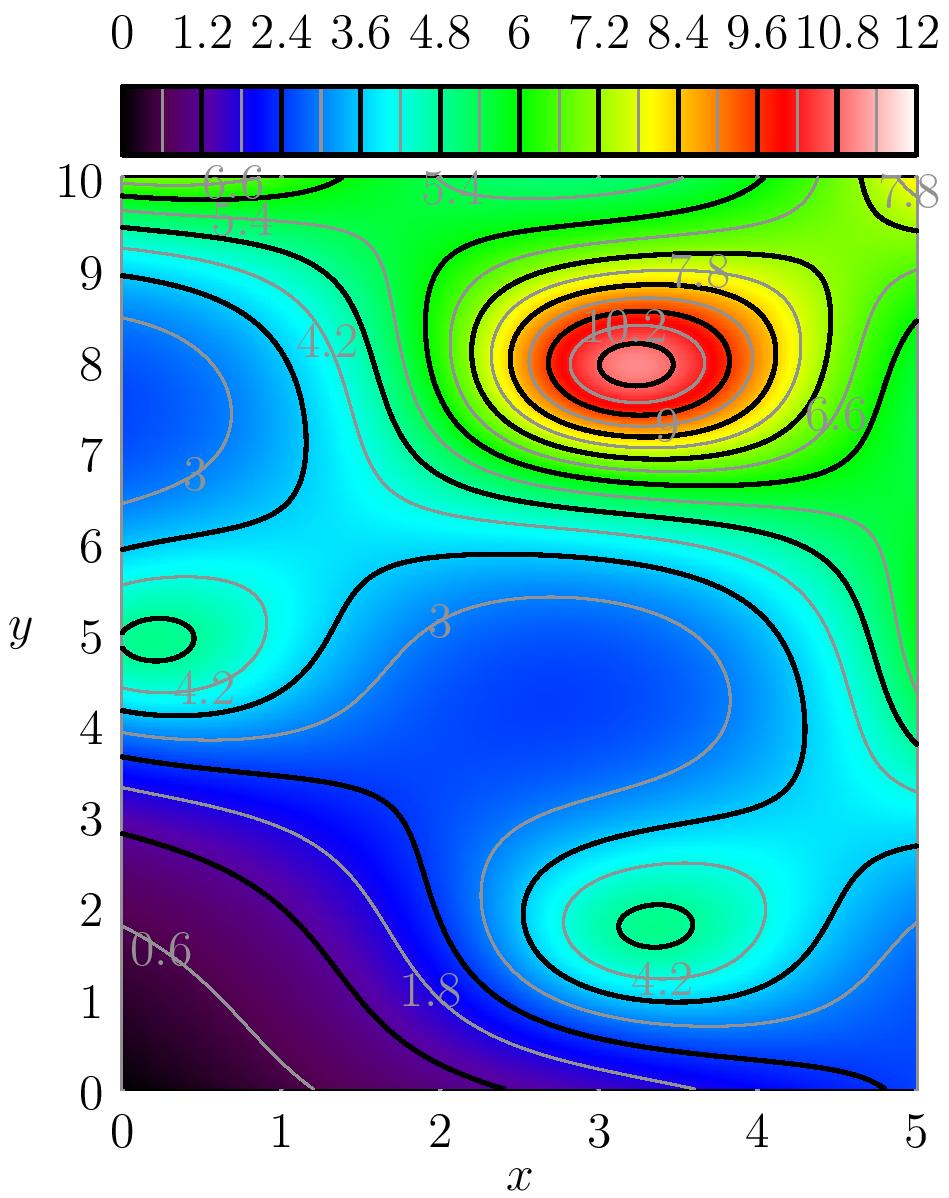
On utilise souvent l'intersection de la surface pour obtenir les lignes de niveau.
Ainsi, les courbes de niveau de $f$ permettent d'avoir une 'présentation' plane de $f$. c.f. exemple
ci-après.
| $\,$ |
|
|
| Surface $z=f(x,y)$ | $\,$ | Lignes de niveau |
Cette représentation est très pratiquée dans les cartes géographiques où la courbe de niveau correspond à l'altitude,
Connaissant les courbes de niveau de $f$ on peut deviner ou imaginer sa représentation dans l'espace (ou la
surface $z=f(x,y)$)
Inversement, si on connaît $f$, on peut avoir des renseignements au moins localement sur ses lignes de
niveau. Plus précisément,
$E$ désigne le plan $\R^2$ muni de sa structure affine euclidienne canonique et rapporté au repère
orthonormal $(O,\vec{i},\vec{j})$.
On considère dans la suite une fonction $F$ définie sur un ouvert $U\subset\R^2$ à valeurs dans $\R$.
Si $\dfrac{\partial F}{\partial\,y}(x_0,y_0)\neq 0$, alors il existe des intervalles ouverts $I,\,J$ tels
que,
$$x_0\in I,\,\,y_0\in J,\,\,I\times J\subset U$$
De plus, il existe une fonction $\varphi\in \CC^1(I,J)$ et une seule, telle que
$$\forall (x,y)\in I\times J,\,\, F(x,y)=0\Longleftrightarrow y=\varphi (x).$$
- Quitte à remplace $F$ par $F-k$ on peut toujours se ramener au cas du théorème i.e. $F(x_0,y_0)=0$.
- Bien évidement, si $\dfrac{\partial F}{\partial\,y}(x_0,y_0)= 0$ alors $\dfrac{\partial F}{\partial\,x}(x_0,y_0)\neq 0$ puisque $\ud F(x_0,y_0)\neq 0$, donc le théorème précédent reste valable en échangeant les rôles entre $x$ et $y$. i.e. existe des intervalles ouverts $I,\,J$ tels que, $$y_0\in I,\,\,x_0\in J,\,\,J\times I\subset U$$ De plus, il existe une fonction $\varphi\in \CC^1(I,J)$ et une seule, telle que $$\forall (y,x)\in J\times I,\,\, F(x,y)=0\Longleftrightarrow x=\varphi (y).$$
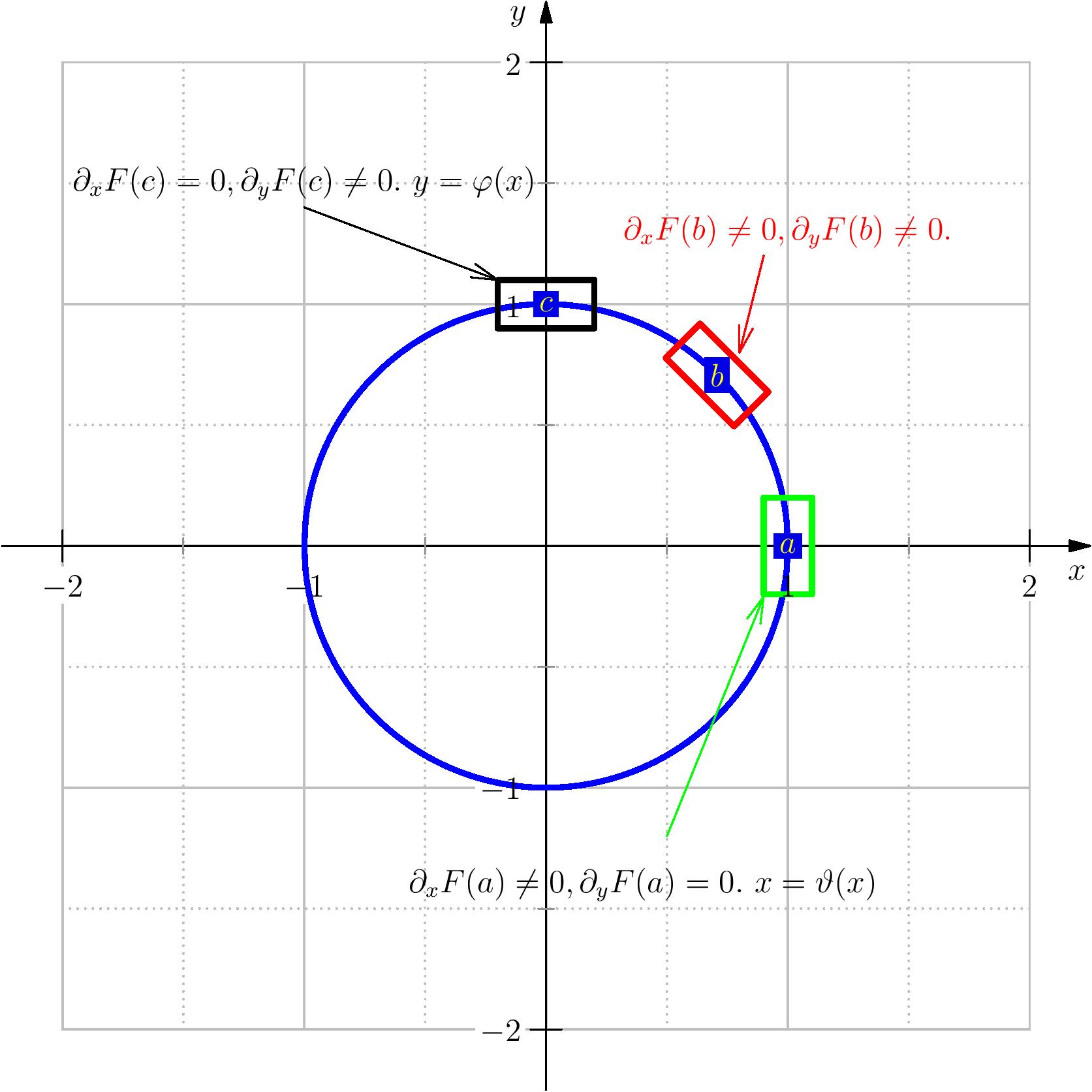
On considère $F(x,y)=x^2+y^2-2$ définie sur $\R^2$, et on a $$\forall (x,y)\in \R^2,\,\dfrac{\partial F}{\partial x}(x,y)=2x,\,\,\dfrac{\partial F}{\partial y}(x,y)=2y.$$ L'ensemble $\Gamma=\{(x,y)\in \R^2,\,\,F(x,y)=0\}$ correspond au cercle unité. Considérons les points suivants $a=(1,0),\,b=(1/\sqrt{2},1/\sqrt{2}),\,$ et $c=(0,1)$. Ces trois points appartiennent à $\Gamma$.
- Au point $a$, $\dfrac{\partial F}{\partial y}(a)=0$, tandis que $\dfrac{\partial F}{\partial x}(a)\neq 0$ donc le théorème précédent permet d'affirmer qu'on peut écrire $x$ en fonction de $y$, i.e. il existe un voisinage $I$ de $0$ et une fonction $\vartheta$ de $I$ dans un voisinage de $1$, tel que $x=\vartheta(y)$. Avec $\vartheta(0)=1$ (on sait dans ce cas qu'on peut écrire $x=\sqrt{1-y^2}$).
- Au point $b$, $\dfrac{\partial F}{\partial y}(b)\neq 0$, et $ \dfrac{\partial F}{\partial x}(b)\neq 0$ donc le théorème précédent permet d'affirmer qu'on peut écrire $x$ en fonction de $y$, ou $y$ en fonction de $x$.
- Au point $c$, $\dfrac{\partial F}{\partial x}(c)=0$, tandis que $\dfrac{\partial F}{\partial y}(c)\neq 0$donc le théorème précédent permet d'affirmer qu'on peut écrire $y$ en fonction de $x$, i.e. il existe un voisinage $I$ de $0$ et une fonction $\varphi$ de $I$ dans un voisinage de $1$, tel que $y=\varphi(x)$. Avec $\varphi(0)=1$ (on sait dans ce cas qu'on peut écrire $y=\sqrt{1-x^2}$ et $I=]-1,1[$).
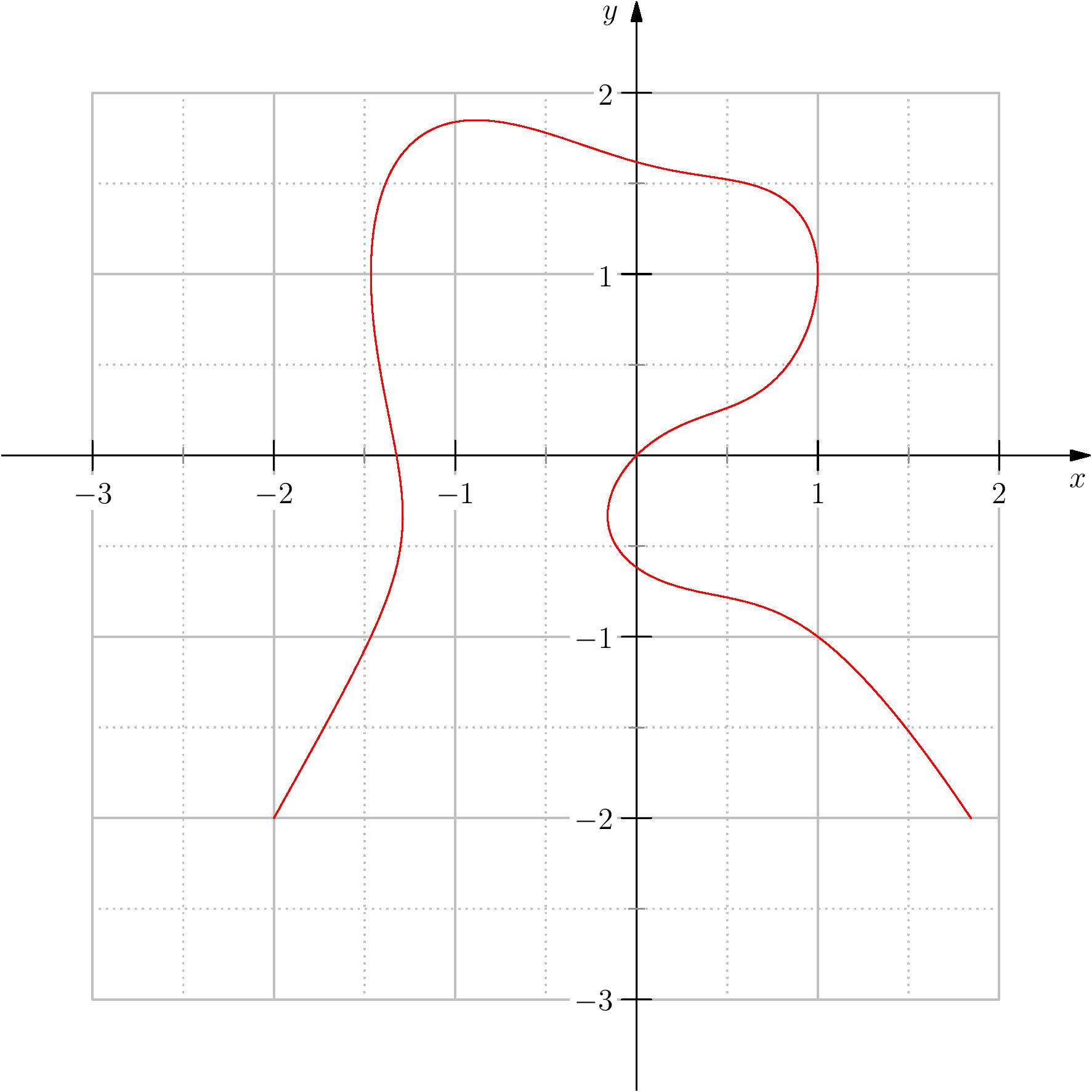
On considère $f(x, y) = x^4 + y^3 - x^2 -y^2 + x - y$. Dans ce cas,
$$\forall (x,y)\in \R^2,\,\dfrac{\partial f}{\partial x}(x,y)=4x^3-2x+1,\,\,\dfrac{\partial f}{\partial
y}(x,y)=3y^2-2y-1.$$
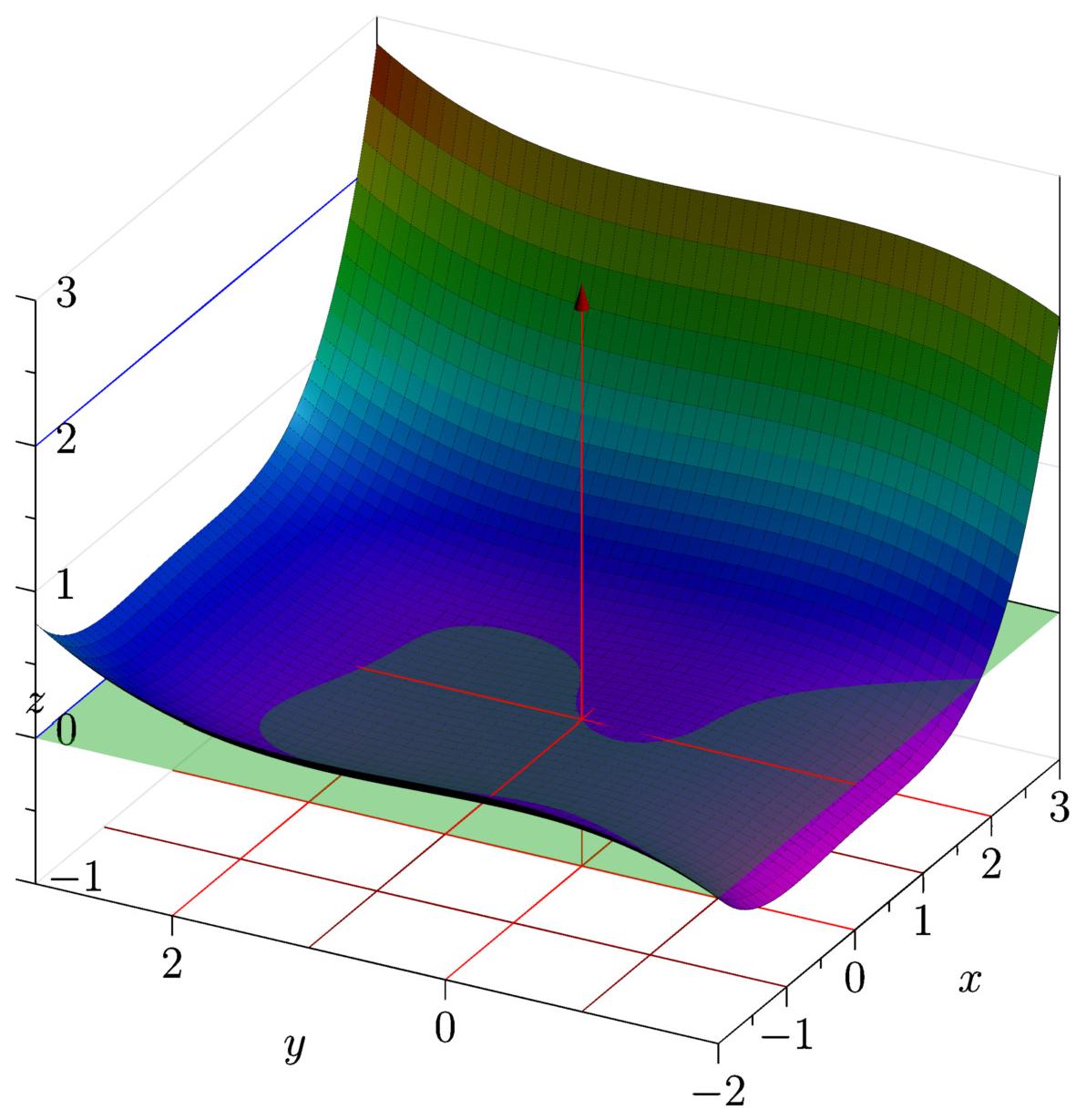
|
$\,$ |
|
| Surface représentative de $f$ | $\,$ | Ligne de niveau $0$ |
Le théorème précédent nous dit que par exemple au voisinage de $(0,0)$, on peut exprimer $y$ en fonction de $x$.
Dans l'exemple précédent, le point $O=(0,0)\in \Gamma$, de plus,
$$\dfrac{\partial f}{\partial x}(O)=1,\,\,\dfrac{\partial f}{\partial y}(O)=-1\Longrightarrow
\varphi'(0)=1.$$
Ainsi, on peut écrire, $\varphi(x)=x+\underset{x\to 0}{\mathrm{o}}(x)$.
Dans notre cas, on peut chercher un DL de $\varphi$ d'ordre supérieur (il y a des théorèmes qui
donne la régularité de $\varphi$ en fonction de $f$). Pour cela, on écrit $\varphi(x)=\dsum_{k=0}^n
a_kx^k+\underset{x\to 0}{\mathrm{o}}(x^k)$ puis on remplace dans la relation vérifiée par $\varphi$, ce
qui donne
$$f(x,\varphi(x))=0\Longrightarrow f(x, \dsum_{k=0}^n a_kx^k)=0,$$
soit dans notre cas:
$$x^4+(\dsum_{k=0}^n a_kx^k)^3-x^2-(\dsum_{k=0}^n a_kx^k)^2+x-(\dsum_{k=0}^n a_kx^k)=0$$
Ensuite on développe à l'ordre $k$, par exemple pour $k=3$, on obtient $\varphi(x)= 0+1x+ax^2+bx^3$,
ensuite,
$$x^4+ (x+ax^2+bx^3)^3-x^2-(x+ax^2+bx^3)^2+x-(x+ax^2+cx^3)=0$$
On note $\Gamma=\{(x,y)\in U,\,F(x,y)=0\}$.
soit après simplification,
$$x^4-x^3-x^2-(x^2+2ax^3)-ax^2-cx^3=0\Longrightarrow a=-2,\,b=-3$$
Pour les courageux, vous pouvez faire le DL de $\varphi$ à l'ordre 5.
$$
\,$$
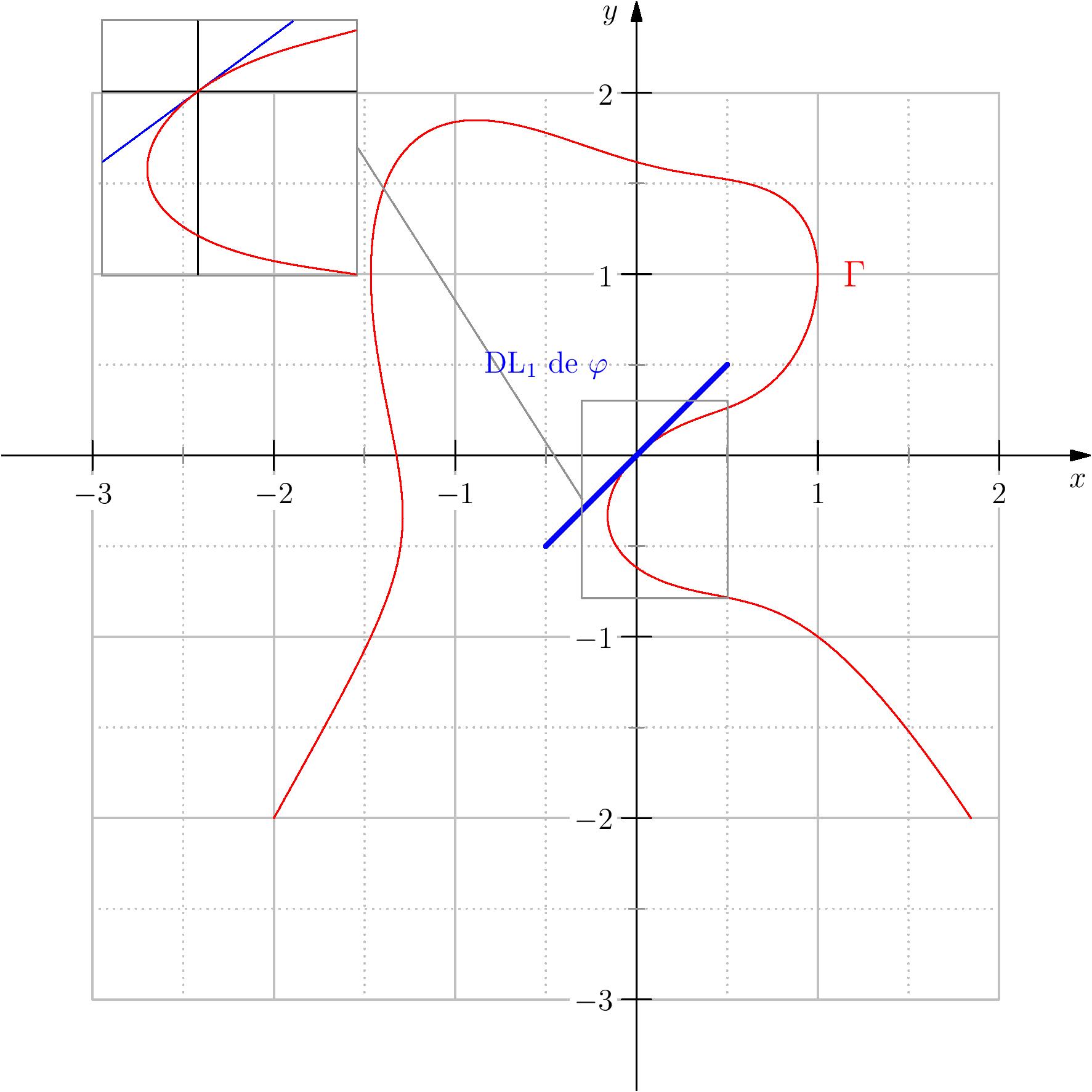
|
$\,$ |
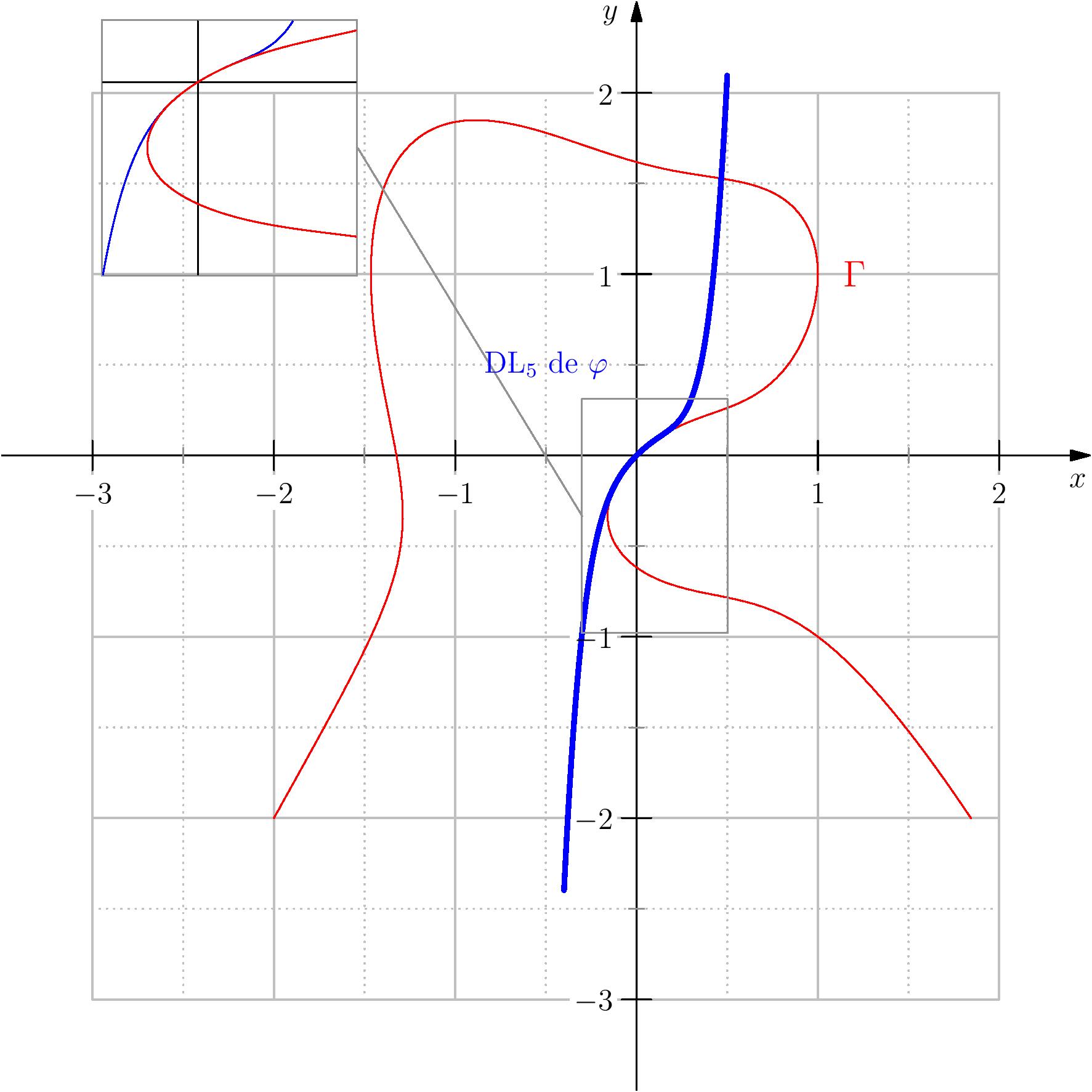
|
| DL$_1$ de $\varphi$ | $\,$ | DL à l'ordre 5 |
C'est équivalent à la définition que nous avons déjà vue avec les courbes paramétrées. Elle est adaptée à la définition de la courbe!
- Le vecteur $(-\frac{\partial F}{\partial\,y}(x_0,y_0),\frac{\partial F}{\partial\,x}(x_0,y_0))$ dirige la tangente.
- Le vecteur $(\frac{\partial F}{\partial\,x}(x_0,y_0),\frac{\partial F}{\partial\,y}(x_0,y_0))$ dirige la normale.
- L'équation de la tangente à $\Gamma $ au point $M_0$ est donnée $$(x-x_0)\frac{\partial F}{\partial\,x}(x_0,y_0)+(y-y_0)\frac{\partial F}{\partial\,y}(x_0,y_0))=0.$$
Soit $f:I\longmapsto\R$ une fonction de classe $\CC^1$, on sait alors que pour tout $x\in I$, $C_f$ admet
une tangente au
point $(x_0,f(x_0))$ d'équation $y=f'(x_0)(x-x_0)+f(x_0)$.
On peut également définir $F:I\times \R\longmapsto \R$ tel que $F(x,y)=y-f(x)$, de sorte que
$C_f=\{(x,y)\in \R^2,\,F(x,y)=0\}$. Comme
$$\dfrac{\partial F}{\partial x}(x,y)=-f'(x),\,\dfrac{\partial F}{\partial y}(x,y)=1$$
donc tout les points de $C_f$ sont réguliers. De plus pour $(x_0,y_0)\in C_f$ l'équation de la tangente
est donnée par:
$$(x-x_0)\frac{\partial F}{\partial\,x}(x_0,y_0)+(y-y_0)\frac{\partial
F}{\partial\,y}(x_0,y_0))=0\Longrightarrow -(x-x_0)f'(x_0)+(y-y_0)=0.$$
On retrouve la 1ère relation! (puisque $y_0=f(x_0)$)
Surface d'équation $F(x,y,z)=0$
Il existe un voisinage $V$ de $M_0$ et un ouvert $D$ de $\R^2$ contenant $(x_0,y_0)$ et une fonction $h\in
\CC^1(D,\R)$ tels que
$$(x,y,z)\in S\cap V\Longleftrightarrow (x,y)\in D\text{ et } z=h(x,y).$$
- Ce théorème se traduit par: Au voisinage de $M_0$ la surface $S$ coïncide avec la graphe de la fonction $\fonct{h}{D}{\R}{(x,y)}{h(x,y)}$.
- Par symétrie, si on suppose$\dfrac{\partial F}{\partial x}(x_0,y_0,z_0)\neq 0$ (resp. $\dfrac{\partial F}{\partial y}(x_0,y_0,z_0)\neq 0$) alors $S$ coïncide localement avec la graphe de $x=f(y,z)$ (resp. $y=g(x,z)$)
Soit $h:\R^2\longmapsto\R$ une application de classe $\CC^1$. On considère la surface $S$ d'équation $S=\{(x,y,z)\in \R^3,\,z=h(x,y)\}$. Montrer que tous les points de $S$ sont réguliers.
On définit $\fonct{F}{\R^3}{\R}{(x,y,z)}{z-h(x,y)}$. Il est clair que $F$ est de classe $\CC^1$ sur $\R$, de plus $S=\{(x,y,z)\in \R^3,\,F(x,y,z)=0\}$. D'autre part, on a $$\forall (x,y,z)\in \R^3,\quad \nabla F(x,y,z)=\begin{pmatrix} -\dfrac{\partial h}{\partial x}(x,y)\\ -\dfrac{\partial h}{\partial y}(x,y)\\ 1 \end{pmatrix}$$ En particulier, pour tout $M\in S,\, \nabla F(M)\neq \overrightarrow{0}$.
On considère la surface $S=\{(\ee^u,\ee^v,uv);\,u,v\in \R\}$. M.q tout point de $S$ est régulier, et déterminer le plan tangent en tout point $M(u,v)\in S$.
$M(x,y,z)\in S$ ssi $x>0,\,y>0$ et $z=\ln(x)\ln(y)$. On peut alors écrire $S=\{(x,y,z)\in U,\,
z-\ln(x)\ln(y)\}$ avec $U=\R_+^*\times\R_+^*\times\R$
Notons $F(x,y,z)=z-\ln(x)\ln(y)$, on obtient,
$$\forall M(x_0,y_0,z_0)\in M,\quad \dfrac{\partial F}{\partial
x}(M)=-\dfrac{\ln(y_0)}{x_0},\,\dfrac{\partial F}{\partial y}(M)=-\dfrac{\ln(x_0)}{y_0},\,\dfrac{\partial
F}{\partial z}(M)=-1.$$
Donc l'équation du plan tangente à $S$ passant par $M$ est,
$$(x-x_0)\dfrac{-\ln(y_0)}{x_0}+(y-y_0)\dfrac{-\ln(x_0)}{y0}-(z-z_0)=0,$$
ou encore,
$$y_0\ln(y_0)(x-x_0)+x_0\ln(x_0)(y-y_0)+x_0y_0(z-z_0)=0.$$
Remarque : On aurait pu trouver l'équation du plan tangente sans passer par la définition de $S$
sous la forme $F(x,y,z)=0$. En effet, on note $M(u,v)= (\ee^u,\ee^v,uv)$, on a $M\in \CC^1(\R^2,\R^3)$ et
$$\dfrac{\partial M}{\partial u }(u,v)=\begin{pmatrix}
\ee^u\\0\\v
\end{pmatrix};\,\dfrac{\partial M}{\partial v }(u,v)=\begin{pmatrix}
0\\\ee^v\\u
\end{pmatrix}$$
Donc le vecteur normal au plan tangente à $S$ en $M(u,v)$ est
$$ \dfrac{\partial M}{\partial u }(u,v)\wedge\dfrac{\partial M}{\partial v }(u,v)=\begin{pmatrix}
-v\ee^v\\ -u \ee^u\\ \ee^{u+v}
\end{pmatrix}\neq 0$$
Ce qui donne l'équation du plan tangente,
$$-v\ee^v(x-\ee^u)-u\ee^u(y-\ee^v)+\ee^{u+v}(z-uv)=0.$$
On retrouve la même relation: puisque $x_0=\ee^u,\, y_0=\ee^v$ et $z_0=\ln(x_0)\ln(y_0)=uv$.
Trouver les points sur le paraboloïde $z=4x^2 +y^2$ où le plan tangent est parallèle au plan $x+2y+z=6$. Même question avec le plan $3x+5y-2z=3$.
Le plan tangent à la surface d'équation
$z=f(x,y)$ au point $(x_0,y_0,z_0)$
est donné par l'équation
$$
z-z_0=\frac{\partial f}{\partial x}(x_0,y_0) (x-x_0)
+\frac{\partial f}{\partial y}(x_0,y_0)
(y-y_0) .
$$
Suivant l'indication,
le plan tangent à la surface d'équation
$z=4x^2 +y^2$ au point $(x_0,y_0,z_0)$
est donné par l'équation
$$\begin{array}{ll}
z&=z_0 +8x_0 (x-x_0) + 2y_0 (y-y_0)
\\
&= 8x_0x +2y_0 y +z_0 - 8x^2_0 - 2y^2_0=
8x_0x +2y_0 y - z_0
\end{array}
$$
Ce qui donne finalement,
$$
z-8x_0x -2y_0 y = z_0.
$$
Pour que
ce plan soit parallèle au plan d'équation $x+2y+z=6$ il faut et il
suffit que
$(1,2)=(-8x_0, -2y_0)$ d'où que $x_0=-1/8$ et $y_0=-1$.
Par conséquent,
le point cherché sur le paraboloïde $z=4x^2 +y^2$
est le point
$(-1/8,-1,17/16)$.
De même,
pour que
le plan \eqref{Ptg2}
soit parallèle au plan d'équation $3x+5y-2z=3$ il faut et il
suffit que
$(3/2,5/2)=(8x_0, 2y_0)$ d'où que $x_0=3/16$ et $y_0=5/4$,
et le point cherché sur le paraboloïde $z=4x^2 +y^2$
est alors le point
$(3/16,5/4,9/64+25/16)$ =$(3/16,5/4,109/64)$.
Déterminer les plans tangents à la surface $S$ d'équation : $z^3 - x.y = 0$ , et contenant la droite $D :\{ x = 2 , y = 3.z + 3\}$.
On pose $F(x,y,z)=z^3-xy$, $F$ est de classe $\CC^1$ sur $\R^3$, et on a $$\forall (x,y,z)\in \R^3,\, \dfrac{\partial F}{\partial x}(x,y,z)=-y,\, \dfrac{\partial F}{\partial y}(x,y,z)=-x,\,\dfrac{\partial F}{\partial z}(x,y,z)=3z^2.$$ Ainsi pour tout $M_0=(x_0,y_0,z_0)\neq (0,0,0)$ l'équation du plan tangent à $S$ passant par $M_0$ est donnée par: $$P:\quad y_0(x-x_0)+x_0(y-y_0)-3z_0^2(z-z_0)=0$$ Pour que $D\subset P$, il faut que pour tout point $(2,3z+3,z)\in Dy$, vérifie: $$y_0(2-x_0)+x_0(3z+3-y_0)-3z_0^2(z-z_0)=0=2x_0-2x_0y_0+3x_0+3z(x_0-z_0^2)+3z_0^3$$ ce qui donne (vu que $z_0^3=x_0y_0$), $$3z(x_0-z_0^2)+2y_0+3x_0+x_0y_0=0\Longrightarrow (x_0=z_0^2) \text{ et }2y_0+3x_0+x_0y_0=0$$ La relation $x_0=z_0^2$ donne $z_0^3-z_0^2y_0=0$ donc
-
Soit $z_0=0$ ce qui implique $x_0=0$ puis $y_0\in \R$, si $y_0=0$ ce qui impossible car il n'y a pas
du plan tangent à $S$ en $(0,0,0)$. Si $y_0\neq 0$ alors l'équation du plan $P$ est $y_0x=0$ et dans
ce cas $P$ ne contient pas $D$
Conclusion si $z_0=0$ il n'y a pas de solutions. -
Soit $y_0=z_0$, en remplaçant dans la deuxième relation, on trouve $2z_0+3z_0^2+z_0^3=0$ ce qui
implique $\xcancel{z_0=0},\, z_0=-1$ ou $z_0=-2$
- Pour $z_0=-1$, $x_0=1,\,y_0=-1$. L'équation du $P$ est $-x+y-3z-1=0$, et on a $D\subset P$.
- Pour $z_0=-2$, $x_0=4,\,y_0=-2$. L'équation du $P$ est $-2x+4y-12z-8=0$, et on a $D\subset P$.
Conclusion, il y a deux solutions.
Extremums relatifs
Si $f$ admet un extremum local en $a$ alors $\nabla f(a)=0$.
Ceci est une condition nécessaire mais pas suffisante.
Exemple, $f(x,y)=xy$ et $a=(0,0)$.
- Si $H_f(a)\in \mathcal{S}_p^{++}(\R)$, alors $f$ atteint un minimum local strict en $a$.
- Si $H_f(a)\not\in \mathcal{S}_p^{+}(\R)$, alors $f$ n'a pas de minimum en $a$.
On peut aussi (en appliquant le résultat précédent à $-f$), déduire
- Si $-H_f(a)\in \mathcal{S}_p^{++}(\R)$, alors $f$ atteint un maximum local strict en $a$.
- Si $-H_f(a)\not\in \mathcal{S}_p^{+}(\R)$, alors $f$ n'a pas de maximum en $a$.
On définit $f:(x,y)\mapsto x^3+y^3-3xy$. Étude des points critiques, puis des extremums éventuels.
$$\nabla f(x,y)=\overrightarrow{0}\Leftrightarrow \left\{\begin{array}{l} x^2=y\\ y^2=x \end{array} \right. \Longleftrightarrow (x,y)=(0,0) \text{ ou } (1,1).$$ Les points critiques sont $\{(0,0,),(1,1)\}$.
- Soit $x>0$ assez proche de $0$, on a $$f(x,x)=2x^3-3x^2< 0=f(0,0),\quad f(x,-x)=3x^2>0=f(0,0).$$ On en déduit que le point $(0,0)$ n'est pas un extremum de $f$.
- Soit $(h,k)\in \R^2$ assez proche de $(0,0)$, on a $$\begin{array}{lcl} f(1+h,1+k)&=&(1+h)^3+(1+k)^3-3(1+h)(1+k)\\ &=&1+3h+3h^2+h^3+1+3k+3k^2+k^3-3(1+k+h+hk)\\ &=&-3-3hk+3h^2+3k^2+k^3+h^3\\ &=&f(1,1)+3 \left(\left(\dfrac{h}{2}-k\right)^2+\dfrac{3h^2}{4}\right)+\underset{(h,k)\to (0,0)}{\mathrm{o}}(\norme{(h,k}) \end{array} $$ On en déduit que le point $(1,1)$ est un extremum local
On note $f$ la fonction $(x,y)\longmapsto x^2y+\ln(4+y^2)$.
- Montrer que $f$ admet sur $\R^2$ un unique point critique.
- On note $g:x\longmapsto f(x,x^3)-f(0,0)$. Trouver un équivalent simple de $g$ en $0$.
- $f$ admet-elle des extremums locaux ?
$$\nabla f(x,y)=\overrightarrow{0}\Leftrightarrow \left\{\begin{array}{rcl}
xy&=&0\\
x^2+\dfrac{2y}{4+y^2}&=&0
\end{array}
\right. \Longleftrightarrow (x,y)=(0,0).$$
Le point critique de $f$ est $\{(0,0)\}$.
Soit $x \in \R$ assez proche de $0$, on a
$$g(x)=f(x,x^3)=x^3+\ln(4+x^6)=x^3+\ln(4)+\ln(1+\frac{x^6}{4})=\ln(4)+x^3+\underset{x\to
0}{\mathrm{0}}(x^3).$$
En particulier, pour $x< 0$, $g(x)< g(0)$ et pour $x>0,\, g(x)>g(0)$. On en déduit que $f$ n'admet pas
des extremums.
On note $f$ la fonction définie sur $\R^2$ par $f(x,y)=(x^2+y^2)(x^2+y^2-8)$.
Déterminer les éventuels extremums locaux et globaux de $f$.
$f$ est de classe $\CC^2$ sur $\R^2$. Pour chercher les extremums de $f$, il faut d'abord trouver ses points critiques. $$\dfrac{\partial f}{\partial x}(x,y)= 4x(x^2+y^2-4),\quad \dfrac{\partial f}{\partial y}(x,y)= 4y(x^2+y^2-4).$$ Ainsi, les points critiques de $f$ sont $$(0,0) \text{ et } \{(x,y)\in \R^2,\,\, x^2+y^2=4\}.$$ D'autre part, on a $$\left\{ \begin{array}{lcl} \dfrac{\partial^2 f}{\partial x^2}(x,y)&=& 12x^2+4y^2-16\\ \dfrac{\partial^2 f}{\partial y^2}(x,y)&=& 12y^2+4x^2-16\\ \dfrac{\partial^2 f}{\partial x\partial y}(x,y)&=& 8xy \end{array} \right. $$
- Au point $(0,0)$, on a $$s=0,\, r=-16,\, t=-16 \Longrightarrow s^2-rt \lt 0$$ donc $f$ admet un maximum local en $(0,0)$, et comme $f(x,x)=2x^2(2x^2-8)\tendvers{x}{\infty}\infty$ alors $f$ n'admet pas un maximum global en $(0,0)$.
- Pour tout $(x,y)\in \R^2$ tel que $x^2+y^2>4$, on a $f(x,y)>4(4-8)=-16$. d'autre part, sur $C=\{(x,y)\in \R^2,\,x^2+y^2\leq 4\}$, $f$ atteint ses bornes (fonction continue sur un fermé borné), donc $f$ admet un minimum global sur $C$ et celui-ci est atteint sur les points critiques de $f$, autrement dit $\{(x,y)\in \R^2,\,\, x^2+y^2=4\}$ (l'autre possibilité $(0,0)$ ne donne pas un minimum).