Etude locale des fonctions
Limites
Définitions
limite en $a$ selon
$A$ ssi il existe $\ell\in F$ tel que
$$ \forall \eps >0,\ \exists \alpha>0, \forall x \in A, \ \norme{x-a}_E < \alpha \Longrightarrow
\norme{f(x)-\ell}_F < \eps.$$
Remarque
La définition ci-dessus peut aussi s'écrire
$$\forall \eps >0,\ \exists \alpha>0 \text{ tq } \forall x \in A, \ x\in B(a,\alpha)\Longrightarrow f(x) \in B(\ell,\eps)$$
ou encore, puisque toute boule ouverte de centre $x$ est un voisinage de $x$ et que tout voisinage de $x$
contient une boule ouverte de centre $x$ :
$$\forall V \in \mathscr{V}(\ell),\ \exists U\in \mathscr{V}(a) \text{ tq } f(U\cap A)\subset V$$
L'avantage de cette écriture est qu'elle peut s'adapter aux cas $a=+\infty$ lorsque $E=\R$ et $D=\N$ (cas des suites), $a=\pm\infty$ lorsque $E=\R$ et $\ell=\pm \infty$ lorsque $F=\R$.
unique .
On note alors $\boxed{\ell=\dsp\dsp\lim_{\substack{x \to a \\x\in A}}f(x)}.$
Remarques
-
Si $A=D$, $\dsp\lim_{\substack{x \to a \\x\in A}}f(x)$ se note simplement $\dsp\lim_{x \to a}f(x)$.
-
Si $A=D$ et si $a\in D$: si $\dsp\lim_{x \to a}f(x)$ existe, ça ne peut être que $f(a)$.
-
Si $A=D\setminus\{a\}$ (c'est le cas le plus courant), la limite, si elle existe, est notée $\dsp\lim_{\substack{x \to a \\x\neq a}}f(x)$.
Exemple
Soit $D=\{(x,y)\in \R^2,\,x>0, y>0\}$, $A=\{(x,x),\,x>0\}$, $a=(0,0)$ et $f:D\longmapsto\R$ définie par
$f(x,y)=\dfrac{xy}{x^2+y^2}$.
Alors, pour tout $z=(x,x)\in A$, on a
$$f(z)=f(x,x)=\dfrac{x^2}{x^2+x^2}=\dfrac{1}{2}$$
On en déduit que
$$\dsp\lim_{\substack{x \to a \\x\in A}}f(x)=\dfrac{1}{2}.$$
bornée sur $A$ au voisinage de $a$ , c'est-à-dire :
$$\exists M\in\R_+^*,\,\, \exists U\in\mathscr{V } (a)\text{ tels que~}\forall x\in U\cap A,\,\, \norme{f(x)}_F\leq M.$$
Remarque
Dans le cas particulier des suites, on retrouve ici le résultat: toute suite convergente est bornée.
Remarque
Dans le cas $E=\R$, on retrouve le fait que, si $f$ est définie au voisinage de $a$ et admet une limite en $a$, alors elle y admet la
même limite à droite et à gauche.
Exemples
-
Dans le cas des suites: $(u_n)$ converge ssi $(u_{2n})$ et $(u_{2n+1})$ convergent vers la même limite.
-
Dans le cas d'une fonction d'une variable réelle: $\dsp\lim_{x\to a}f(x)$ existe ssi $\dsp\lim_{x \to a^+}f(x)$ et
$\dsp\lim_{x \to a^{-}}f(x)$ existent et sont égales.
-
$f$ admet la limite $\ell$ en $a$ selon $A$.
-
Pour toute suite $(x_n)_{n\in\N}$ d'éléments de $A$ qui converge vers $a$, la suite $\big(f(x_n)\big)_{n\in\N}$
converge vers $\ell$.
Remarque
D'après le théorème Car. seq. de l'adhérence , si $f$ admet une limite $\ell$ en $a$ alors $\ell\in \overline{f(A)}$.
La définition ci-dessus peut aussi s'écrire $$\forall \eps >0,\ \exists \alpha>0 \text{ tq } \forall x \in A, \ x\in B(a,\alpha)\Longrightarrow f(x) \in B(\ell,\eps)$$ ou encore, puisque toute boule ouverte de centre $x$ est un voisinage de $x$ et que tout voisinage de $x$ contient une boule ouverte de centre $x$ : $$\forall V \in \mathscr{V}(\ell),\ \exists U\in \mathscr{V}(a) \text{ tq } f(U\cap A)\subset V$$ L'avantage de cette écriture est qu'elle peut s'adapter aux cas $a=+\infty$ lorsque $E=\R$ et $D=\N$ (cas des suites), $a=\pm\infty$ lorsque $E=\R$ et $\ell=\pm \infty$ lorsque $F=\R$.
- Si $A=D$, $\dsp\lim_{\substack{x \to a \\x\in A}}f(x)$ se note simplement $\dsp\lim_{x \to a}f(x)$.
- Si $A=D$ et si $a\in D$: si $\dsp\lim_{x \to a}f(x)$ existe, ça ne peut être que $f(a)$.
- Si $A=D\setminus\{a\}$ (c'est le cas le plus courant), la limite, si elle existe, est notée $\dsp\lim_{\substack{x \to a \\x\neq a}}f(x)$.
Soit $D=\{(x,y)\in \R^2,\,x>0, y>0\}$, $A=\{(x,x),\,x>0\}$, $a=(0,0)$ et $f:D\longmapsto\R$ définie par $f(x,y)=\dfrac{xy}{x^2+y^2}$. Alors, pour tout $z=(x,x)\in A$, on a $$f(z)=f(x,x)=\dfrac{x^2}{x^2+x^2}=\dfrac{1}{2}$$ On en déduit que $$\dsp\lim_{\substack{x \to a \\x\in A}}f(x)=\dfrac{1}{2}.$$
Dans le cas particulier des suites, on retrouve ici le résultat: toute suite convergente est bornée.
Dans le cas $E=\R$, on retrouve le fait que, si $f$ est définie au voisinage de $a$ et admet une limite en $a$, alors elle y admet la même limite à droite et à gauche.
- Dans le cas des suites: $(u_n)$ converge ssi $(u_{2n})$ et $(u_{2n+1})$ convergent vers la même limite.
- Dans le cas d'une fonction d'une variable réelle: $\dsp\lim_{x\to a}f(x)$ existe ssi $\dsp\lim_{x \to a^+}f(x)$ et $\dsp\lim_{x \to a^{-}}f(x)$ existent et sont égales.
- $f$ admet la limite $\ell$ en $a$ selon $A$.
- Pour toute suite $(x_n)_{n\in\N}$ d'éléments de $A$ qui converge vers $a$, la suite $\big(f(x_n)\big)_{n\in\N}$ converge vers $\ell$.
D'après le théorème Car. seq. de l'adhérence , si $f$ admet une limite $\ell$ en $a$ alors $\ell\in \overline{f(A)}$.
On suppose que $F$ est de dimension finie $p$ et soit $\BB=(b_1,\cdots,b_p)$ une base de $F$.
Opérations sur les limites
Continuité
Continuité en un point
- Dire que $f$ est continue en $a$ peut s'écrire: $$\forall\varepsilon>0,\,\, \exists\alpha>0,\,\,\forall x\in D, \,\,\norme{x-a}_E < \alpha\Longrightarrow \norme{f(x)-f(a)}_F \leq \varepsilon.$$ ou encore $$\forall V \in \mathscr{V}(f(a)),\ \exists U\in \mathscr{V}(a) \text{ tel que } f(U\cap D) \subset V.$$
- La notion de voisinage étant une notion topologique, l'écriture précédente montre que la notion de continuité est inchangée si on remplace l'une des normes (dans $E$ ou $F$) par une norme équivalente.
Ce résultat peut être utilisé pour montrer qu'une application $f$
On considère $f$ définie par $f(0)=0$ et $f(x)=\sin(\frac{1}{x})$ pour $x\neq 0$. On considère les deux suites: $$u_n=\dfrac{1}{\frac{\pi}{2}+2n\pi},\quad v_n=\dfrac{1}{\frac{\pi}{4}+2n\pi}$$ il est clair que $u_n\tendversN\,0$ et $v_n\tendversN\,0$, tandis que $$f(u_n)=\sin\left(\frac{\pi}{2}+2n\pi\right)=1,\, f(v_n)=\sin\left(\frac{\pi}{4}+2n\pi\right)=\dfrac{1}{\sqrt{2}}$$ donc $f$ n'est pas continue en $0$.
On suppose que $F$ est de dimension finie, et $\BB=(b_1,\cdots,b_p)$ une base de $F$. (c.f. définition ci-dessus)
Continuité globale
Soient $E,F$ deux $\K$-EVN et $f:E\longmapsto F$. Montrer que : $f$ est continue ssi pour tout $A\subset E$, $f(\overline{A})\subset \overline{f(A)}$.
$\Longrightarrow\,$ Supposons que $f$ est continue, soit $A\subset E$ non vide et $x\in \overline{A}$, alors il existe une suite
$(x_n)$ d'éléments de $A$ telle que $x_n\tendversN\,x$, comme $f$ est continue alors $f(x_n) \,(\in f(A)) \tendversN\, f(x)$ ce qui implique
$f(x)\in \overline{f(A)}$.
$\Longleftarrow\,$ Supposons que $f$ vérifie : pour tout $A\subset E$, $f(\overline{A})\subset \overline{f(A)}$.
Supposons qu'il existe $x\in E$ tel que $f$ n'est pas continue en $x$. i.e $\dsp\lim_{z\to x}f(z)\neq f(x)$. Ainsi,
$$\exists \varepsilon >0,\,\forall r>0,\, \,\exists z\in B(x,r),\quad \norme{f(z)-f(x)}_F\geq \varepsilon.$$
Pour $n\in \N^*$, on pose $r=\frac{1}{n}$ dans la relation précédente, donc il existe $z_n\in E$ tel que $\norme{z-x}_E \leq \dfrac{1}{n}$ et
$\norme{f(z_n)-f(x)}_F\geq \varepsilon$.
On note maintenant $A=\{z_n,\,n\geq 1\}$, alors $x\in \overline{A}$ car $z_n\tendversN x$ mais $f(x)\not\in \overline{f(A)}$ ce qui est absurde.
Donc $f$ est continue sur $E$.
- Pour tout $f,g\in \CC(D,F)$ et $\lambda,\,\mu\in \K$, on a $\lambda f+\mu g\in \CC(D,F)$, autrement dit, $\CC(D,F)$ est un sev de $\mathscr{A}(D,F)$.
- Soient $f\in \CC(D,F)$ et $g\in \CC(\Delta,G)$, on suppose que $f(D)\subset \Delta$ alors $g\circ f\in \CC(D,G)$.
- Soit $f\in \CC(D,F)$ et $\varphi\in \CC(A,\K)$ alors $\varphi f\in \CC(A,F)$, de plus si $\varphi$ ne s'annule pas sur $D$ alors $\frac{1}{\varphi}f\in \CC(D,F)$.
Soit $n\geq 1$, Pour $i\in \inter{1,n}$ on note $\fonct{p_i}{\K^n}{\K}{(x_1,\cdots,x_n)}{x_i}$ est une fonction continue sur $\K^n$ (on peut montrer la continuité en utilisant la définition ou en utilisant la caractérisation des application linéaire continue c.f. théorème suivant). En utilisant le résultat précédent, on trouve $$\forall (a_1,\cdots,a_n)\in \N^n,\forall \lambda\in \K,\, \fonct{f}{\K^n}{\K}{(x_1,\cdots,x_n)}{\lambda x_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}} \in \CC(\K^n,\K).$$ Plus généralement, tout fonction polynomiale en les cordonnées de $x$ est une fonction continue.
Soient $f\in \CC(\R,\R)$ et $D=\R^*\times \R$. On définit sur $D$ la fonction $g$ par: $$\forall (x,y)\in D,\quad g(x,y)=\dfrac{1}{x}\int_x^{xy}f(t)\ud t.$$ Montrer que $g$ est continue sur $D$. Peut-on prolonger $g$ par continuité sur $\R^2$?
Comme $f$ est continue sur $\R$, alors $f$ admet une primitive sur $\R$, qu'on note $F$ ($F\in \CC^1(\R,\R)$ et $F'=f$). On note aussi $\fonct{p_1}{\R^2}{\R}{(x,y)}{x}$ et $\fonct{p_2}{\R^2}{\R}{(x,y)}{y}$. Il est clair que $p_1, p_2$ sont continues sur $D$, de plus $p_1$ ne s'annule pas sur $D$ donc $1/p_1$ est aussi continue sur $D$. On peut alors écrire $g=\dfrac{F\circ (p_1p_2)-F\circ p_1}{p_1}$, ceci prouve que $g$ est continue sur $D$. D'autre par, pour tout $x\neq 0$ et $y\neq 0$, on a $$\begin{array}{lcl} g(x,y)&=&\dfrac{F(yx)-F(x)}{x}=\dfrac{F(yx)-F(0)+F(0)-F(x)}{x-0}\\ &&\\ &=&y\dfrac{F(yx)-F(0)}{yx-0}-\dfrac{F(x)-F(0)}{x-0}\tendvers{x}{0}yF'(0)-F'(0) \end{array} $$ Comme $F'(0)=f(0)$, alors $g(x,y)\tendvers{x}{0} (y-1)f(0)$. Ce résultat reste vrai si $y=0$ puisque $g(x,0)=\dfrac{-1}{x}\dsp\int_0^xf(t)\ud t\tendvers{x}{0}-f(0)$. On en déduit qu'on peut prolonger $g$ par continuité sur $\R^2$, on posant $g(0,y)=(y-1)f(0)$.
- $f$ est continue sur $E$.
- l'image réciproque par $f$ de tout ouvert de $F$ est un ouvert de $E$.
- l'image réciproque par $f$ de tout fermé de $F$ est un fermé de $E$.
- C'est un résultat important, qu'on utilise souvent pour déterminer si un ensemble est un ouvert (ou fermé).
- Il faut faire attention, dans ce théorème on utilise l'image réciproque et à ne pas confondre avec l'image direct. En effet, l'image direct d'un ouvert (res. fermé) par une application continue n'est pas forcément un ouvert (resp. un fermé).
- Soient $f,g:\R \longrightarrow\R$, continues. Alors (par exemple) $$\big\{ x\in \R \text{ tq } f(x) < g(x)\big\} \text{ est un ouvert de} \R.$$ $$\big\{ x\in \R \text{ tq } f(x)\leqslant g(x)\big\}\text{ est un fermé de }\R.$$
- Soit $f\in\CC(\R,\R)$ et soient $$\begin{array}{ll} \Gamma&=\big\{(x,y)\in\R^2 \text{ tq } y=f(x)\big\} \text{ le graphe de } f\\ \mathscr{E}&=\big\{(x,y)\in\R^2 \text{ tq } y\geqslant f(x)\big\} \text{ l'épigraphe de } f\\ \mathscr{E}'&=\big\{(x,y)\in\R^2 \text{ tq } y > f(x)\big\} \end{array} $$ Alors $\Gamma$ et $\mathscr{E}$ sont des parties fermées de $\R^2$ et $\mathscr{E}'$ est une partie ouverte de $\R^2$.
- $f:\R\longmapsto\R$ définie par $f(x)=\sin(x)$, alors $f(\R)=[-1,1]$ donc l'image directe d'un ouvert dans ce cas est un fermé.
- $f:\R\longmapsto \R$, définie par $f(x)=\Arctan (x)$, alors $f(\R)=]-\pi/2,\pi/2[$ donc l'image directe d'un fermé dans ce cas est un ouvert.
Soient $\Omega=\{\begin{pmatrix} a&c\\b&d \end{pmatrix}\in \MM_2(\R),\, (a-d)^2+4bc>0\}$ et $F=\{\begin{pmatrix} a&c\\b&d \end{pmatrix}\in \MM_2(\R),\, (a-d)^2+4bc\geq 0\}$. Montrer que $\Omega$ est un ouvert de $\MM_2(\R)$ et $F$ est un fermé de $\MM_2(\R)$.
On définie la fonction $f$ de $\MM_2(\R)$ dans $\R$ par $f(A)= (a-d)^2+4bc$ si $A=\begin{pmatrix} a&c\\b&d \end{pmatrix}$. $f$ est une fonction polynomiale en les cordonnées de $A$ donc $f$ est continue sur $\MM_2(\R)$. Il suffit après d'écrire $\Omega=f^{-1}(\R_+^*)$ et $F=f^{-1}(\R_+)$.
Soit $E$ un evn
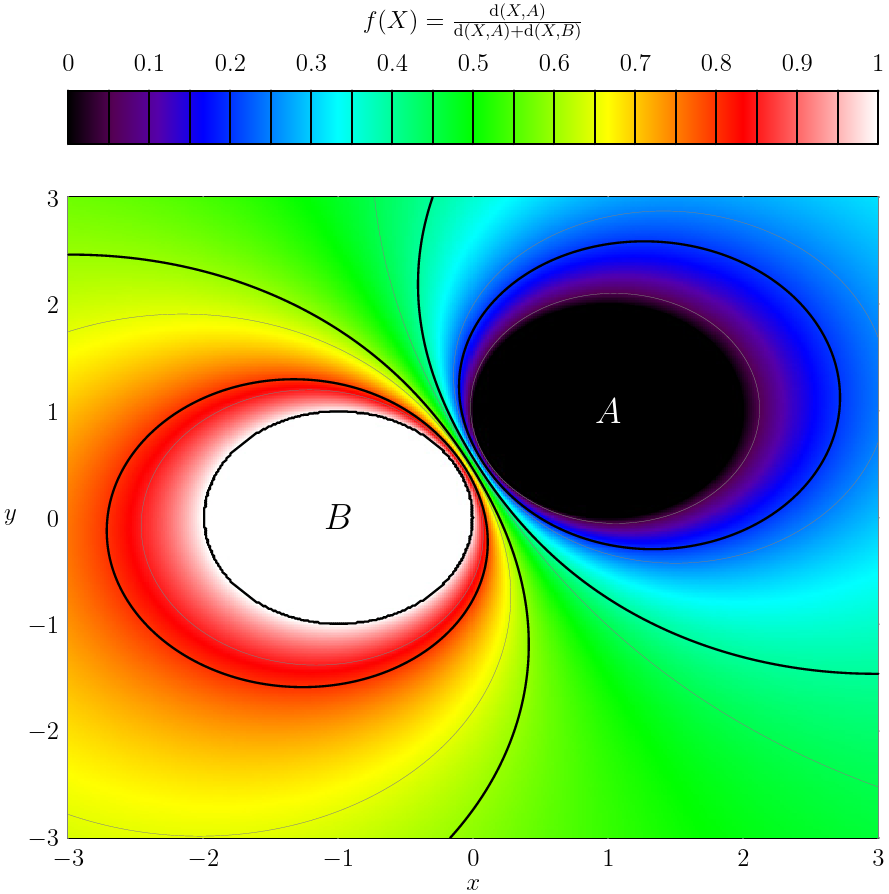
- Soient $A,\,B$ deux fermés non vides de $E$. Montrer que: $$A\cap B =\emptyset \Longleftrightarrow \forall x\in E,\quad \ud (x,A)+\ud (x,B)\neq 0.$$
- On suppose que $A\cap B=\emptyset$. Construire une application $f$ continue de $E$ dans $\R$ telle que $f_{\mid A}=0$ et $f_{\mid B}=1$. En déduire l'existence de deux ouverts disjoints $U$ et $V$ tels que $A\subset U$ et $B\subset V$.
- On sait que $\ud (x,A)=0\Leftrightarrow x\in \overline{A}$, puisque $A$ et $B$ sont fermés alors $\overline{A}=A$ et $\overline{B}=B$. Donc en utilisant la première remarque, on a: $$\begin{array}{lcl} \ud (x,A)+\ud (x,B)=0&\Longleftrightarrow & \ud (x,A)=0=\ud (x,B)\\ &\Longleftrightarrow & x\in A \text{ et }x\in B\\ & \Longleftrightarrow & x\in A\cap B \end{array}$$ On en déduit donc, $A\cap B=\emptyset$ ssi $\forall x\in E,\quad \ud (x,A)+\ud (x,B)>0$.
- On définit $f$ par, $$\forall x\in E,\,\,f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}.$$ $f$ est bien définie puisque $\ud (x,B)+\ud (x,A)>0$. De plus $f$ est continue sur $E$, puisque $x\mapsto \ud(x,A)$ (resp. $x\longmapsto \ud(x,B)$) sont continues sur $E$. D'autre part, on a: $$\forall x\in A,\quad f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}=\dfrac{0}{\ud (x,B)}=0,$$ $$ \forall x\in B,\quad f(x)=\dfrac{\ud (x,A)}{\ud (x,B)+\ud (x,A)}=\dfrac{\ud (x,A)}{\ud (x,A)}=1.$$
Posons maintenant $U=f^{-1}(]-\infty,\frac{1}{2}[),\,\, V=f^{-1}(]\frac{1}{2},\infty[)$, comme $f$ est continue on a $U,\,V$ sont des ouverts de $E$ et clairement $U\cap V=\emptyset$ et $A\subset U,\,\,B\subset V$.
Fonctions lipschitzienne
Le rapport $k$ défini ci-dessus n'est pas unique: on peut en effet remplacer $k$ par n'importe quel réel plus grand. Plus précisément, soit $A=\left\{ \dfrac{\norme{f(x)-f(y)}_F}{\norme{x-y}_E}, \ (x,y)\in D^2, \ x\neq y \right\}$; alors $f$ est lipschitzienne ssi l'ensemble $A$ est majoré; les réels $k$ tels que $f$ soit $k$-lipschitzienne sont alors les majorants de $A$. Le meilleur rapport de lipschitziannité de $f$ est alors le plus petit de ces majorants, i.e la borne supérieure de $A$.
- L'application $\fonct{\norme{\cdot}}{E}{\R}{x}{\norme{x}}$ est $1$-lipschitzienne, en effet, on a: $$\forall x,y\in E,\quad \Big| \norme{x}-\norme{y} \Big| \leqslant \norme{x-y}. $$
- Soit $A$ une partie non vide de $E$, l'application distance à $A$, $\fonct{d_A}{E}{\R}{x}{\ud (x,A)}$ est $1$-lipschitzienne.
- L'ensemble des applications lipschitziennes de $D$ dans $F$ est un sev de $\mathscr{A}(D,F)$.
- La composée d'applications lipschitziennes est lipschitzienne.
Soient $E$ un $\K$-evn et $T:E \to E$ définie par $T(u) = \left\{ { \begin{array}{ll} u & {{\text{si }}\left\| u \right\| \leqslant 1} \\ {\frac{u}{{\left\| u \right\|}}} & {{\text{sinon}}} \\ \end{array} } \right.$. Montrer que $T$ est 2-lipschitzienne.
Soient $u,v\in E$,
- Si $\norme{u}\leq 1$ et $\norme{v}\leq 1$, on a immédiatement $$\norme{T(u)-T(v)}=\norme{u-v}\leq 2\norme{u-v}.$$
- Si $\norme{u}> 1$ et $\norme{v}> 1$, en utilisant le résultat de l'exercice sur les normes, on trouve: $$\norme{T(u)-T(v)}= \norme{\dfrac{u}{\norme{u}}-\dfrac{v}{\norme{v}}}\leq \max(\norme{u},\norme{v})\norme{\dfrac{u}{\norme{u}}-\dfrac{v}{\norme{v}}}\leq 2\norme{u-v}.$$
- Si $\norme{u}\leq 1$ et $\norme{v}>1$, on a alors: $$\begin{array}{lcl} \norme{T(u)-T(v)}&=& \norme{u-\dfrac{v}{\norme{v}}}=\norme{u-v+v-\dfrac{v}{\norme{v}}}\\ &\leq & \norme{u-v}+\norme{\left(1-\frac{1}{\norme{v}}\right)v}=\norme{u-v}+\norme{v}-1\\ &\leq & \norme{u-v}+\norme{v}-\norme{u}\leq 2\norme{u-v} \end{array}$$
- Si $\norme{v}\leq 1$ et $\norme{u}>1$, ce cas est équivalent au cas précédent.
Donc, dans tous les cas, on a: $\norme{T(u)-T(v)}\leq 2\norme{u-v}$ ce qui prouve le résultat.
La réciproque est fausse.
- l'équation $f(x)=x$ admet
une et une seule solution $\ell \in D$ . - Pour tout $u_0 \in D$, la suite définie par la relation de récurrence
$u_{n+1 } =f(u_n)$ converge vers $\ell$ .
Applications linéaires continues
- $u$ est continue.
- $u$ est continue en $0_E$.
- Il existe un réel $k> 0$ tel que, pour tout $x\in E$, $\norme{u(x)}\leq k\norme{x}$.
- On peut remplacer la propriété 3 par $u$ est $k$-lipschitzienne.
- On peut montrer aussi que $u$ est continue ssi $u$ est bornée sur la sphère unité.
Soient $E$ et $F$ deux espaces vectoriels normés et $f \in \LL(E,F)$. On suppose que, pour toute suite $(u_n )$ tendant vers $0$, $f(u_n )$ est bornée. Montrer que $f$ est continue.
Supposons que $f$ n'est pas continue, alors $$\forall n\in \N^*,\, \exists x_n E\setminus\{0\},\,\, \norme{f(x_n)}_F\geq n\norme{x_n}_E.$$ On pose alors $z_n=\dfrac{x_n}{\sqrt{n}\norme{x_n}_E}$, on a $\norme{z_n}=\dfrac{1}{\sqrt{n}}$ donc $z_n\tendversN\,0$. D'autre part, on a $$\norme{f(z_n)}_F= \norme{f\left(\dfrac{x_n}{\sqrt{n}\norme{x_n}_E}\right)}_F=\dfrac{1}{\sqrt{n}\norme{x_n}_E}\norme{f(x_n)}_F\geq \dfrac{n\norme{x_n}_E}{\sqrt{n}\norme{x_n}_E}=\sqrt{n}\tendversN\,\infty$$ ce qui contredit l'hypothèse. Donc $f$ est continue.
Soit $E$ un $\K$-espace vectoriel de dimension finie. Montrer que toutes les normes sur $E$ sont équivalents.
Soient $N_1,\,N_2$ deux normes définies sur $E$. Puisque $E$ est de dimension finie, alors $\ide$ est continue de $(E,N_1)$ dans $(E,N_2)$, donc, $$ \tag{$\star$} \exists K_1>0,\quad \forall x\in E,\, N_1(\ide (x))=N_1(x)\leq K_1 N_2(x). $$ De même $\ide$ est continue de $(E,N_2)$ dans $(E,N_1)$, donc, $$ \tag{$\star\star$} \exists K_2>0,\quad \forall x\in E,\, N_2(\ide (x))=N_2(x)\leq K_2 N_1(x). $$ Les relations ($\star$) et ($\star\star$) impliquent que les deux normes $N_1$ et $N_2$ sont équivalentes.
Soit $E=\R_n[X]$ muni de la norme suivante $\norme{P}=\sup\{\abs{P(t)},\,t\in [0,1]\}.$ Montrer la relation suivante: $$\exists c>0,\quad \forall P\in E,\, \abs{P(2019)+P(2020)} \leq c\int_0^1 \abs{P(t)}\ud t.$$
L'application $\fonct{\varphi}{E}{\R}{P}{P(2019)+P(2020)}$ est linéaire donc continue puisque $E$ est de dimension finie. D'après la caractérisation des applications linéaires continues, il existe $K>0$, tel que pour tout $P\in E$, on a $\abs{\varphi(P)}\leq K\norme{P}$. D'autre part, l'application qui à $P$ associé $\dsp\int_0^1\abs{P}$ définie une norme sur $E$ donc équivalente à la norme déjà définie. On en déduit alors $$\exists \alpha>0,\quad \forall P\in E,\quad \norme{P}\leq \alpha \int_0^1\abs{P(t)}\ud t.$$ Il suffit alors de prendre $c=\alpha \times K$.
- Si $E$ est un ev de dimension $n$ rapporté à une base $\mathscr{B}$, l'application $\det_{\mathscr{B}}$ qui à toute famille de $n$ vecteurs de $E$ associe son déterminant dans la base $\mathscr{B}$ est continue.
- Dans $\MM_n(\K)$, l'application qui à deux matrices $A$ et $B$ associe leur produit $AB$ est bilinéaire continue.
- $E$ est un espace préhilbertien réel, alors $\fonct{\varphi}{E\times E}{\R}{(x,y)}{\langle x|y \rangle}$ est une forme bilinéaire continue.