Espaces préhilbertiens réel
Dans ce chapitre $E$ désigne un $\R$-espace vectoriel.
Généralités
Formes bilinéaire, produit scalaire
- $E=\R^n$, avec $n\in \N^*$. On pose $\varphi_1(x,y)=\dsum_{i=0}^nx_iy_i$ pour tout $x=(x_1,\cdots,x_n) $ et $y=(y_1,\cdots,y_n)$ dans $E$. Alors $\varphi_1$ est une fbs.
- $E=\R[X]$, $x_1,\cdots,x_n\in \R$ avec $n\in \N^*$, on définit $\varphi$ par: $$\forall P,Q\in E,~~\varphi_2(P,Q)=\dsum_{k=1}^nP(x_i)Q(x_i).$$ Alors $\varphi$ est une fbs.
- $E=\CC^1([0,1],\R)$ et $\varphi_3$ définie par $\varphi_3(f,g)=\dsp\int_0^1f'(t)g'(t)\ud t$.
- $E=\MM_n(\R)$ et $\varphi_4(A,B)=\tr ( A^\top B)$ pour tout $A,B\in E$.
- La forme quadratique associée à $\varphi_1$ sur $\R^n$ est $q_1:(x_1,\cdots,x_n)\longmapsto \dsum_{i=1}^nx_i^2$.
- La forme quadratique associée à $\varphi_2$ sur $\R[X]$ est $q_2:P\longmapsto \dsum_{i=1}^nP(x_i)^2$.
- La forme quadratique associée à $\varphi_3$ sur $\CC^1([0,1],\R)$ est $q_3:f\longmapsto \dsp\int_0^1f'(t)^2\ud t$.
- La forme quadratique associée à $\varphi_4$ sur $\MM_n(\R)$ est $q_4:A\longmapsto \tr(A^\top A)$.
$\varphi$ est définie positive ssi pour tout $x\in E\setminus \{0\}$, on a $\varphi(x,x)>0$ (ou $q(x)>0$).
- Soient $E=\R[X]$ et $\varphi(P)=\dsum_{k=1}^nP(x_k)Q(x_k)$. Alors $\varphi$ n'est pas définie positive car si on prend $P=\dsp\prod_{1\leq i\leq n}(X-x_i)$ on a $P\neq 0$ et $\varphi(P,P)=0$.
- $E=\CC([0,1])$ et $\varphi(f,g)=\dsp\int_0^1f(t)g(t)\ud t$, alors $\varphi$ est définie positive.
Soit $A=\begin{pmatrix} 1&2\\ 2&1 \end{pmatrix}$. On considère $\varphi$ définie sur $\R^2\times\R^2$ par $\varphi(x,y)= x^\top Ay$.
M.q $\varphi$ est une fbs. $\varphi$ est-t-elle définie positive?
Soient $X=\begin{pmatrix} a\\b \end{pmatrix},\, Y=\begin{pmatrix} c\\d \end{pmatrix}\in \R^2$. On a $$ \varphi(X,Y)=\begin{pmatrix} a &b \end{pmatrix}\begin{pmatrix} 1&2\\ 2&1 \end{pmatrix}\begin{pmatrix} c\\d \end{pmatrix} = \begin{pmatrix} a &b \end{pmatrix}\begin{pmatrix} c+2d\\2c+d \end{pmatrix} = ac+2ad+2bc+bd.$$ $$ \varphi(Y,X)=\begin{pmatrix} c &d \end{pmatrix}\begin{pmatrix} 1&2\\ 2&1 \end{pmatrix}\begin{pmatrix} a\\b \end{pmatrix} = \begin{pmatrix} c &d \end{pmatrix}\begin{pmatrix} a+2b\\2a+b \end{pmatrix} = ac+2bc+2ad+bd.$$ Ainsi, $\varphi$ est symétrique.
On aurait pu aussi écrire (puisque $\varphi(X,Y)\in \R$) $$\varphi(X,Y)=\varphi(X,Y)^\top=\left(X^\top AY\right)^\top=Y^\top\,A^\top \,X=Y^\top\,A\,X=\varphi(Y,X).$$ Soient $X,\,Y,Z\in \R^2$ et $\lambda\in \R$, on a $$\varphi(X,Y+\lambda Z)=X^\top\, A(Y+\lambda Z)=X^\top\,AY+\lambda X^\top\, AZ =\varphi(X,Y)+\lambda \varphi(X,Z)$$ Ainsi, la fonction $\fonct{\,}{\R^2}{\R}{Y}{\varphi(X,Y)}$ est linéaire. Comme $\varphi$ est symétrique alors $\varphi$ est bilinéaire.
Soit $X=\begin{pmatrix} a\\b \end{pmatrix}\in \R^2$, on a $$\varphi (X,X)= \begin{pmatrix} a &b \end{pmatrix} \begin{pmatrix} 1&2\\ 2&1 \end{pmatrix}\begin{pmatrix} a\\b \end{pmatrix} = a^2+4ab+b^2 =(a+b)^2+2ab$$ en particulier, si $b=-a\neq 0$, on a $X\neq 0$ et $\varphi (X,X)> 0$ donc $\varphi$ n'est pas définie positive.
Lorsque $\varphi$ est un produit scalaire, on note plus souvent $(x\mid y)$ ou $\langle x,y\rangle$ ou $x\cdot y$ à la place de $\varphi(x,y)$.

(Centrale 2022)
Dans la Q 2., 4 points précis sont attendus pour démontrer qu’une application est un produit
scalaire.
En particulier, la positivité ne consiste pas à démontrer que $\tr(𝐴^\top 𝐵) \geq 0 $. Rappelons par ailleurs que
la trace d’un produit n’est en général pas égale au produit des traces ! Enfin, il est important de faire
la différence entre un produit scalaire et une norme.

(Centrale 2023)
Dans la question 46, elle aussi très classique, les 4 points de la définition d’un produit scalaire n’ont
parfois pas été démontrés correctement. En particulier, la positivité du
produit scalaire ne signifie pas
que $\tr(AB) \geq 0$ pour toutes les matrices $𝐴$ et $𝐵$.
Soit $\fonct{\varphi }{ \mathbb{R}_n[X]^2} {\mathbb{R}}{ (P,Q) } {\dsum_{k=-2017}^{2017}P(k)Q(k)}$. Quelles sont les valeurs de $n$ pour lesquelles $\varphi$ est un produit scalaire ?
Il est clair que $\varphi$ est une fbs, de plus, $$\forall P\in \R_n[X],\,\varphi(P,P)=\dsum_{k=-2017}^{2017}P(k)^2\geq 0.$$ Donc $\varphi$ est positive.
Soit $P\in \R_n[X]$ tel que $\varphi (P,P)=0$, cela implique que $P(k)=0$ pour tout $k\in \inter{-2017,2017}$, ainsi $P$ a au moins 4035 racines distincts, ce qui est possible si $n\geq 4035$.
Ainsi, pour que $\varphi$ soit un produit scalaire sur $\R_n[X]$ il faut que $n$ vérifie $n\leq 4034$.
On appelle
Norme euclidienne associée à un p.s
Soit $E$ un espace préhilbertien réel, on note $q$ la forme quadratique définie sur $E$ associée au produit scalaire. On définit sur $E$ l'application $\norme{\cdot}$ par : Pour tout $x\in E$,$\norme{x}=\sqrt{q(x)}$.
$\norme{}$ est bien définie puisque $q(x)=\langle x,x\rangle\geq 0$.
Démonstration
Soient $x,y\in E$. Si $x=0$ alors la relation est vérifiée puisque $q(x)=0$...
Supposons alors que $x\neq 0$. On définit l'application $\fonct{P}{\R}{\R}{t}{q(x+ty)}$. Comme $q$ est définie positive alors $P$ ne prend que des valeurs dans $\R_+$.
Soit $t\in \R$, on a: $$P(t)=\langle (tx+y)\,,\,(tx+y)\rangle\underset{\text{\small Bilinéarité}}{=} t^2q(x)+2t\langle x\,,\,y\rangle+q(y)\geq 0.$$ $P$ est une fonction polynômiale de degré 2; on en déduit que le discriminant de $P$ est $\leq 0$. $$\Delta \leq 0\Longrightarrow \langle \,x,\,y\rangle-q(x)q(y)\leq 0 $$ Ce qui donne : $$ \langle \,x,\,y\rangle\leq q(x)q(y)\Longrightarrow \abs{\scal{x}{y}}\leq \sqrt{q(x)q(y)}=\norme{x}\norme{y}. $$ Cas d'égalité :Supposons que $\abs{\langle\,x\,,\,y\rangle}=\sqrt{q(x)q(y)}=\norme{x}\norme{y}$, alors d'après le raisonnement précédente, $P$ possède une racine réelle (double) $t_0$. Ce qui donne $$0=P(t_0)=q(t_0x+y)\Longrightarrow t_0x+y=0\Longrightarrow (x,y)\text{ est liée}.$$
Soient $n\in \N^*,~~x_1,\cdots,x_n\in \R_+^*$ tels que $\dsum_{k=1}^nx_k=1$. Montrer que : $\dsum_{k=1}^n\dfrac{1}{x_k}\geq n^2$, étudier le cas d'égalité.
On considère $\R^n$ muni de produit scalaire usuel. On note $X=\left(\frac{1}{\sqrt{x_1}},\cdots,\frac{1}{\sqrt{x_n}}\right)$ et $Y=\left(\sqrt{x_1},\cdots,\sqrt{x_n}\right)$.
En utilisant l'inégalité de Cauchy-Schwarz, on a: $$\scal{X}{Y}^2\leq \norme{X}^2\norme{Y}^2\Longrightarrow \left(\dsum_{i=1}^n\dfrac{\sqrt{x_i}}{\sqrt{x_i}}\right)^2\leq \left(\dsum_{i=1}^n\dfrac{1}{x_i}\right)\left(\dsum_{i=1}^nx_i\right)$$ $$\Longrightarrow \boxed{n^2\leq \sum_{i=1}^n\dfrac{1}{x_i}}.$$ De plus, on a égalité ssi la famille $(X,Y)$ est liée, i.e. il existe $\lambda\in \R^*$ tel que: $$Y=\lambda X\Longleftrightarrow \forall k\in \inter{1,n},~~\sqrt{x_k}=\dfrac{\lambda}{\sqrt{x_k}}\Longleftrightarrow x_1=\cdots=x_n.$$ Comme $\dsum_{i=1}^nx_i=1$, on obtient alors $\boxed{x_1=\cdots=x_n=\dfrac{1}{n}}$.
Démonstration
Soient $x,y\in E$, on a $$\norme{x+y}^2=\norme{x}^2+2\langle x\,,\,y\rangle+\norme{y}^2\leq \norme{x}^2+2\norme{x}\norme{y}+\norme{y}^2=(\norme{x}+\norme{y})^2$$ La fonction $t\mapsto t^2$ est strictement croissante sur $\R_+$, on en déduit donc que $\norme{x+y}\leq \norme{x}+\norme{y}$.
On a une égalité dans la relation précédent ssi il existe $\lambda\in \R_+$ tel que $x=\lambda y$.
Soient $x,y\in E$, on a $$ \norme{x}^2+\norme{y}^2=\dfrac{1}{2}\left(\norme{x+y}^2+\norme{x-y}^2\right)$$
Soient $E,F$ deux espace préhilbertiens réels, $f:E\longmapsto F$ une application telle que: $$f(0)=0,~~\forall (x,y)\in E^2,~~\norme{f(x)-f(y)}=\norme{x-y}.$$ Montrer que $f$ est linéaire.
Soit $x\in E$, en prenant $y=0$ dans le relation vérifiée par $f$, on trouve: $$\norme{f(x)-f(0)}=\norme{x-0}\Longrightarrow\norme{f(x)}=\norme{x}.$$ Ensuite, on a, pour tout $x,y\in E$, $$\norme{f(x)-f(y)}^2=\norme{f(x)}^2+2\scal{f(x)}{f(y)}+\norme{f(y)}^2$$ $$\Longrightarrow \norme{x-y}^2=\norme{x}^2+2\scal{f(x)}{f(y)}+\norme{y}^2,$$ on en déduit que, pour tout $x,y\in E$, on a $ \scal{f(x)}{f(y)}=\scal{x}{y}$. Enfin, soient $\lambda\in ,\,x,y\in E$, on a, $$ \begin{array}{lcl} \norme{f(\lambda x+y)-\left(\lambda f(x)+y\right)}^2&=& \norme{f(\lambda x+y)}^2+\lambda^2\norme{f(x)}^2+\norme{f(y)}^2-2\lambda\scal{f(\lambda x+y)}{f(x)}\\ &&-2\scal{f(\lambda x+y)}{f(y)}+2\lambda\scal{f(x)}{f(y)}\\ &&\\ &=&\norme{\lambda x+y}^2+\lambda^2\norme{x}^2+\norme{y}^2-2\lambda\scal{\lambda x+y}{x} -2\scal{\lambda x+y}{y}\\ &&+2\lambda\scal{x}{y}\\ &&\\ &=&\norme{\left(\lambda x+y\right)-\lambda x-y}^2=0 \end{array} $$ On en déduit que $f(\lambda x+y)=\lambda f(x)+f(y)$ soit $\boxed{f\in \LL(E,F)}$.
Orthogonalité
Soit $E$ un espace préhibertien réel muni d'un produit scalaire $\langle\,\cdot,\,\cdot\,\rangle$.
Définitions
Soient $x,y\in E$, on a l'équivalence: $$x\perp y\Longleftrightarrow \norme{x+y}^2=\norme{x}^2+\norme{y}^2.$$
$E=\R^3$, $F=\{(x,y,z)\in \R^3,~~x+y+z=0\}$ et $G=\Vect((1,1,1))$. On a $F\perp G$.
Par exemple, on a $E^{\perp}=\{0\}$ et $\{0\}^\perp =E$.
En effet, si $x\in E^\perp$, alors $x\perp x$ donc $\norme{x}^2=\langle x,x\rangle=0$ soit $x=0$.
Si on a $u\in E$ tel que $\scal{u}{x}=0$ pour tout $x\in E$ alors $u=0$.
Par exemple si on a $$\forall M\in \MM_n(\R),~~\tr (AM)=\tr (BM)\Longrightarrow A=B$$
- $F\cap F^\perp=\{0\}$.
- $F\subset \left(F^\perp\right)^\perp$.
- Si $F\subset G$ alors $G^\perp \subset F^\perp$.
Soient $F,G$ deux sous espaces vectoriels de $E$. Montrer que $(F+G)^\perp=F^\perp\cap G^\perp$.
On a $$ \left.\begin{array}{lcl} F\subset F+G &\Longrightarrow& (F+G)^\perp \subset F^\perp\\ G\subset F+G &\Longrightarrow& (F+G)^\perp \subset G^\perp \end{array}\right\} \Longrightarrow (F+G)^\perp \subset F^\perp\cap G^\perp. $$ Inversement, soit $x\in F^\perp\cap G^\perp$, $y=y_F+y_G\in F+G$, on a $$\langle x\,,\,y\rangle =\langle x\,,\,y_F+y_G\rangle =\langle x\,,\,y_F\rangle+\langle x\,,\,y_G\rangle =0$$ ce qui prouve que $x\in (F+G)^\perp$, ainsi $(F^\perp\cap G^\perp )\subset (F+G)^\perp$ d'où l'égalité.
Famille orthogonale de vecteurs
Démonstration
Une famille est libre ssi toute sous famille finie est libre. Il suffit donc de démontrer ce résultat pour une famille finie.
Soient $n\in \N$ et $(x_1,\cdots,x_n)$ une famille orthogonale. Soient $(a_1,\cdots,a_n)\in \R^n$ tels que $\dsum_{k=1}^na_kx_k=0$, alors, $$\forall k\in \inter{1,n},~~\langle x_k,\sum_{j=1}^na_jx_j\rangle=0=\sum_{j=1}^na_j\langle x_k,x_j\rangle=a_k\norme{x_k}^2$$
-
Soit $x\in E$. On dit que $x$ est
unitaire (ou normé) si $\norme{x}=1$. -
Soit $(x_i)_{i\in I}$ une famille d'éléments de $E$. On dit que cette
famille est
orthonormale (ou orthonormée) ssi $$\forall (i,j)\in I^2,~~~~\langle\,x_i\,,\,x_j\,\rangle=\delta_{i\,j}.$$
Base orthonormale
On suppose que $E$ est de dimension finie, i.e.> $E$ est un espace euclidien.
Soit $\BB=(e_1,\cdots,e_n)$ une base orthonormale de $E$ (on suppose que $\dim(E)=n$). Soit $x\in E$ il existe $a_1,\cdots,a_n\in \R$ tels que $x=\dsum_{k=1}^na_ie_i$, en faisant le produit scalaire de $x$ avec $e_j$ pour $j\in \{1,\cdots,n\}$, on trouve: $$\langle x,e_j\rangle=\langle \dsum_{k=1}^na_ke_k,e_j\rangle=\dsum_{k=1}^na_k\langle e_k,e_j\rangle=\dsum_{k=1}^na_k\delta_{k\,j}=a_j.$$ Ce qui donne le résultat suivant,
Soient $x=\dsum x_ie_i,\,y=\dsum y_ie_i$ deux vecteurs de $E$, en utilisant la bilinéarité de produit scalaire et le faite que $\BB$ est orthonormale, on trouve: $$\langle x,y\rangle= \langle \dsum_{k=1}^nx_ke_k,\dsum_{i=1}^ny_ie_i\rangle= \dsum_{1\leq i,j\leq n}x_iy_j\langle e_i,e_j\rangle= \dsum_{1\leq i,j\leq n}x_iy_j\delta_{i\,j}=\dsum_{i=1}^nx_iy_i.$$ D'où
Soient $x=\dsum x_ie_i,\,y=\dsum y_ie_i$ deux vecteurs de $E$, on note $X=\MM_\BB(x),\,Y=\MM_\BB(y)\in\MM_{n\,1}(\R)$ les matrices colonnes des coordonnées de $x$ et $y$ dans $\BB$. Alors,
- $\langle x,y\rangle=X^\top\cdot Y= Y^\top\cdot X$.
- $\norme{x}^2= X^\top \cdot X=\dsum_{i=1}^nx_i^2$.
On considère $E=\R^3$ muni de produit scalaire canonique. On considère la famille $V=(v_1,v_2,v_3)$ définis par: $$v_1=\frac{1}{\sqrt{2}}(1,1,0),~~~~v_2=\dfrac{1}{\sqrt{6}}(-1,1,-2),~~v_3=\dfrac{1}{\sqrt{3}}(-1,1,1).$$
- Montrer que $V$ est une base orthonormée de $E$.
- Donner les coordonnées de $(x,y,z)$ dans cette base.
- En déduire la matrice de passage de $V$ à la base canonique $\BB$.
Démonstration
On va procéder par récurrence sur $n=\dim (E)\in \N^*$.
Pour $n=1$, on a $\BB=(e_1)$ avec $e_1\neq 0$ car $\BB$ est libre. On pose alors $e_1'=\dfrac{e_1}{\norme{e_1}}$, on a $\Vect(e_1)=\Vect(e_1')$ et $\norme{e_1'}=1$. Donc la relation est vraie pour $n=1$.
Soit $n\geq 1$, supposons que la relation est vraie au rang $n$ et montrons la au rang $n+1$.
Soit $E$ un $\R$-e.v de dimension $n+1$ et soit $\BB=(e_1,\cdots,e_n,e_{n+1})$ une base de $E$. D'après l'hypothèse de récurrence on peut construire une famille $\BB'_n=(e_1',\cdots,e_n')$ orthonormale telle que $\Vect(e_1,\cdots,e_n)=\Vect(e_1',\cdots,e_n')$.
On pose $f_{n+1}=e_{n+1}-\dsum_{k=1}^n\langle e_{n+1},\,e_k'\rangle e_k'$, on a:
- $f_{n+1}$ est non nul, car $e_{n+1}\not\in \Vect(e_1,\cdots,e_n)=\Vect(\BB_n')$. De plus, on a $(e_1',\cdots,e_n',f_{n+1})$ est libre donc base de $E$.
- Pour tout $k\in \inter{1,n}$, on a: $$ \langle f_{n+1},\,e_k'\rangle= \langle \,e_{n+1}-\dsum_{j=1}^n\langle e_{n+1},\,e_j'\rangle e_j',\,e_k'\rangle=\langle \,e_{n+1}\,,e_k'\rangle- \dsum_{j=1}^n\langle e_{n+1},\,e_j'\rangle \langle e_j',\,e_k'\rangle=0$$ Ainsi $f_{n+1}\in \left(\Vect(\BB_n')\right)^\perp$ donc la famille $(e_1',\cdots,e_n',f_{n+1})$ est orthogonale.
- Ce résultat montre que tout espace vectoriel euclidien admet une base orthonormal.
- La méthode de construction de cette base (utilisée dans la démonstration) s'appelle le procédé d'orthonormalisation de Gram-Schmidt.
Soit $E=\R_2[X]$ muni de produit scalaire $\langle P,Q\rangle=\dsp\int_0^1P(x)Q(x)\ud x$. Construire une base orthonormale de $E$ à partir de la base canonique $\BB=(1,X,X^2)$.
On suit la procédé de Gram-Schimdt,
- On pose $e_1'=\dfrac{e_1}{\norme{e_1}}=1$ puisque $\norme{e_1}=\sqrt{\dsp\int_0^1\ud t}=1$.
- On pose $f_2=e_2-\langle e_2,e_1'\rangle e_1'=X-\left(\dsp\int_0^1x\ud x\right)1=X-\frac{1}{2}$, puis $$\norme{f_2}^2=\int_0^1\left(t-\frac{1}{2}\right)^2\ud t=\left[\dfrac{(t-\frac{1}{2})^3}{3}\right]_0^1=\dfrac{1}{24}+\dfrac{1}{24}=\dfrac{1}{12}$$ Donc $e_2'=\dfrac{f_2}{\norme{f_2}}=\sqrt{12}X-\frac{\sqrt{12}}{2}$.
- On pose $f_3=e_3-\langle e_3,e_2'\rangle e_2'-\langle e_3,e_1'\rangle e_1'$, i.e. $$f_3=X^2-\left(\sqrt{12}\int_0^1t^2(t-\frac{1}{2})\ud t\right)\sqrt{12}(X-\frac{1}{2})-\left(\int_0^1t^2\ud t\right)=X^2-(X-\frac{1}{2})-\frac{1}{3}=X^2-X+\frac{1}{6}$$ donc $$\norme{f_3}^2=\int_0^1\left(t^2-t+\frac{1}{6}\right)^2\ud t=\int_0^1\left(t^4+t^2+\dfrac{1}{36}-2t^3+\dfrac{t^2}{3}-\dfrac{t}{3}\right)\ud t=\dfrac{1}{180}$$ Ce qui donne $$e_3'=\sqrt{180}X^2-\sqrt{180}X+\sqrt{5}$$
Démonstration
Soit $f$ une forme linéaire définie sur $E$. On sait que $E$ admet une base orthonormé. Soit $\BB=(e_1,\cdots,e_n)$ une b.o. de $E$. On a $$\forall x\in E,\quad x=\dsum_{i=1}^n\scal{x}{e_i}e_i $$ donc $$\forall x\in E,\quad f(x)=f\left(\dsum_{i=1}^n\scal{x}{e_i}e_i\right) \underset{f\text{ linéaire} }{=} \dsum_{i=1}^n\scal{x}{e_i}f(e_i)=\scal{x}{\dsum_{i=1}^nf(e_i)e_i}.$$ On pose alors $a=\dsum_{i=1}^nf(e_i)e_i$, ceci assure l'existence de $a$.
Pour l'unicité, supposons qu'il existe $b\in E$ tel que $$\forall x\in E,\,\, f(x)=\scal{x}{b}\Longrightarrow \forall x\in E,\,\scal{x}{b}=\scal{x}{a}$$ autrement dit $b=a$.
Soit $n\in \N$, $E=\R_n[X]$ $$,~~\exists! Q\in \R_n[X],~~\forall P\in \R_n[X]~P(0)=\int_0^1Q(t)P(t)\ud t$$ Peut-on généraliser ce résultat à $\R[X]$? Poser $P=n^a(1-X)^n$ puis choisir $a$ t.q $\norme{P_n}\leq 1$...
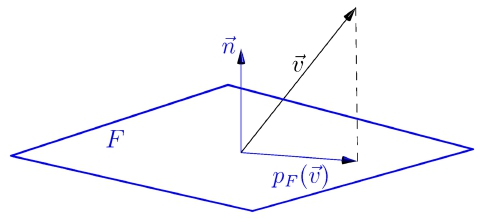
Sommes orthogonales, projection orthogonale
Soit $E$ un espace préhilbertien.
Démonstration
Soit $(x_1,\cdots,x_p)\in \dsp\prod_{k=1}^pF_k$ tel que $\dsum_{k=1}^p x_k=0$. Pour tout $i\in \inter{1,p}$, on a: $$0=\langle x_i,0\rangle=\langle x_i,\dsum_{k=1}^px_k\rangle=\dsum_{k=1}^p\langle x_i,x_k\rangle=\norme{x_i}^2,$$ en effet, puisque les $F_k$ sont orthogonaux entre eux alors $\langle x_i,x_k\rangle=0$ si $i\neq k$.
On en déduit que, pour tout $i\in \inter{1,p}$, $x_i=0$. D'où le résultat.
- Soient $F_1,\cdots,F_p$ des sous espaces vectoriels de $E$, deux à deux orthogonaux. La somme $\dsp\oplus_{i=1}^pF_i$ est appelée somme directe orthogonale des $F_i$.
- Soient $F$ et $G$ deux sous espaces vectoriels de $E$. On dit que $F$ et $G$ sont supplémentaires orthogonaux si $F\perp G$ et $F\oplus G=E$. On note alors $E=F\dsp\overset{\perp}{\oplus} G$.
- Si $\dim E< \infty$ alors on $\dim F^\perp=\dim E-\dim F$.
- Dans ce cas $F=(F^\perp)^\perp$
-
Ce résultat n'est pas vrai si $\dim F=\infty$,
$E=\CC([0,1])$, $\scal{f}{g}=\dsp\int_0^1f(t)g(t)\ud t$ et $F=\R[x]$. Si $f\in F^\perp$ alors $\dsp\int_0^1f(t)t^n\ud t =0$ pour tout $n\in \N$ ce qui implique que $f$ est nulle (densité des fonctions polynômiale). Donc $F^\perp=\{0\}$ et on $F+F^\perp\neq E$ .
De plus si $\BB=(e_1,\cdots,e_n)$ est une base orthonormale de $F$, alors
$$\forall x\in E,~~p_F(x)=\dsum_{i=1}^p\scal{e_i}{x}e_i.$$
Le vecteur $p_F(x)$ est appelé
Soit $x\in E$, l'ensemble $\{\norme{x-y},~~y\in F\}$ est une partie non vide minoré dans $\R$, donc il admet une borne inférieur.
Déterminer $\dsp\underset{(a,b,c)\in \R^3}{\inf}\int_0^1(t^3-at^2-bt-c)^2\ud t$.
$a=3/2,\,b=-5/3,\,c=1/20$.
Distance à un hyperplan
Soit $H$ un hyperplan de $E$, alors il existe $f\in \LL(E,\R)$ tel que $H=\Ker (f)$. Or d'après le théorème de représentation , il existe $a\in E$ tel que $$\forall x\in E,\quad f(x)=\scal{x}{a}$$ donc $$\forall x\in H,\quad 0=f(x)=\scal{x}{a}$$ autrement dit, $a\in H^\perp$, or $\dim (F^\perp)=\dim (E)-\dim (H) =1$ (car $H$ est un hyperplan de $E$), ainsi $H^\perp=\Vect (a)$.
Dans ce cas, le calcul de la projection sur $H$ est plus simple en utilisant un vecteur normal à $H$, en effet, on a la relation suivante: $$ \ide =p_H+P_{H^{\perp}} \text{ ainsi } p_H=\ide -p_{H^{\perp}}.$$ Ce qui donne le résultat suivant:
On définit $\varphi$ sur $\R[X]^2$, par $$\varphi (A,B)=\dsp\int_0^\infty A(t)B(t)\ee^{-t}\ud t.$$
- Montrer que $\varphi$ définit un produit scalaire qu'on notera $\scal{}{}$.
- On note $(P_0,P_1,\cdots,P_n)$ l'orthonormalisée de Gram-Schmidt pour la base canonique de $\R_n[X]$. Calculer $P_i(0)$ pour $i\in \inter{0,n}$ (on pourra s'intéresser à $\scal{P_i}{P_i'}$ ).
- On note $F=\{P\in \R_n[X],\,\, P(0)=0\}$. Calculer $\ud (1,F)$.
-
Notons d'abord que $\varphi$ est bien définie (en effet il s'agit d'une intégrale impropre).
Soient
$A,B\in \R[X]$, la fonction $f:t\mapsto A(t)B(t)\ee^{-t}$ est continue sur $[0,\infty[$, de plus,
$$t^2f(t)\tendvers{t}{\infty}0 \Longrightarrow f(t)=\underset{t\to \infty}{\mathrm{O}}\left(\frac{1}{t^2}\right).$$
Comme $\dsp\int_1^\infty \dfrac{\ud t}{t^2}$ converge, on en déduit que $\dsp\int_0^\infty f(t)\ud t $ converge.
La symétrie et bilinéarité de $\varphi$ sont évident. Montrons que $\varphi$ est définie positive. $$\forall A\in \R[X],\quad \scal{A}{A}=\int_0^\infty A^2(t)\ee^{-t}\ud t \geq 0.$$ Si on a $\scal{A}{A}=0$ alors, pour tout $t\in \R_+$, $A^2(t)\ee^{-t}=0$ (intégrale impropre d'une fonction continue positive), donc $A(t)=0$ (car $\ee^{-t}> 0$), autrement dit le polynôme $A$ admet une infinité de racine ce qui implique que $A=0$. - $(P_0,P_1,\cdots,P_n)$ l'orthonormalisée de Gram-Schmidt pour la base canonique de $\R_n[X]$. On peut prendre $P_0=1$, donc $P_0(0)=1$. $$\,$$ Soit $i\in \inter{1,n}$, on a (en faisant une IPP) $$\begin{array}{lcl} \scal{P_i}{P_i'}&=&\dsp \int_0^\infty P_i(t)P_i'(t)\ee^{-t}\ud t = \left[\dfrac{P_i(t)^2}{2}\ee^{-t}\right]_0^\infty +\dfrac{1}{2}\int_0^\infty P_i(t)^2\ee^{-t}\ud t\\ &&\\ &=& -\dfrac{P_i(0)^2}{2} +\dfrac{1}{2}\norme{P_i}^2= \dfrac{1-P_i(0)^2}{2} \end{array} $$ Or $\deg(P_i')< \deg(P_i)$ ainsi $P_i'\in \Vect (P_0,\cdots,P_{i-1})$, donc $\scal{P_i}{P_i'}=0$. On en déduit alors $P_i(0)^2=1$.\\ Le faite de multiplier $P_i$ par $-1$ ne change pas la nature de cette base, ainsi on peut supposer dans la suite $$\forall i\in \inter{0,n},\quad P_i(0)=1.$$
- $F$ est un hyperplan de $E$,et clairement $1\not \in F$, de plus $1\not\in F^\perp $ car (par exemple ) $\scal{1}{X}=1\neq 0$, notons $Q$ la projection de $1$ sur $F$, on peut écrire : $$Q = \scal{Q}{P_0}P_0+\scal{Q}{P_1}P_1+\cdots +\scal{Q}{P_n}P_n.$$ En utilisant la question précédente, on a : $$\forall i\in \inter{1,n},\quad P_i-1\in F \Longrightarrow \forall i\in \inter{1,n},\quad \scal{1-Q}{P_i-1}=0$$ Ce qui donne $$0 = \scal{1-Q}{P_i-1}=\scal{1}{P_i}-\scal{Q}{P_i}-\scal{1}{1}+\scal{Q}{1}\Longrightarrow \scal{Q}{P_i} =\scal{Q}{1}-1$$ Ainsi, $$Q =\dsum_{k=1}^n \left(\scal{Q}{1}-1\right)P_k +\scal{Q}{1} P_0 .$$ Or $Q(0)=0$ car $Q\in F$, donc $$ 0=\dsum_{k=1}^n \left(\scal{Q}{1}-1\right)P_k(0) +\scal{Q}{1} P_0(0)\Longrightarrow \scal{Q}{1} =\dfrac{n}{n+1}.$$ Finalement, $$\textcolor{blue}{\boxed{Q = \dfrac{n}{n+1}-\dsum_{k=1}^n \dfrac{1}{n+1}P_k}},$$ et $$\textcolor{blue}{\boxed{1-Q = \dfrac{1}{n+1}+\dsum_{k=1}^n \dfrac{1}{n+1}P_k}}.$$ D'après le cours $$\ud (1,F)^2=\norme{1-Q}^2=\dsum_{k=0}^n\scal{1-Q}{P_k}^2 =\dsum_{k=0}^n\dfrac{1}{(n+1)^2}=\dfrac{1}{n+1} $$ On obtient donc, $$\textcolor{blue}{\boxed{\ud (1,F)=\sqrt{\dfrac{1}{n+1}}}}.$$