Les décimaux de $\dfrac{\pi^2}{6}$
Le début de l'histoire
En regardant une page web Wikipedia j’ai pu lire qu' Euler a calculé les $20$ décimales de la somme de $\dsum_{n=1}^\infty \dfrac{1}{n^2}$.
A première vue, cela semble normal, 20 décimales ce n'est pas grande chose, mais en regardant de près, c’est impressionnant.
En effet, cette série converge lentement, une estimation de reste $R_n$ donne $R_n \in ]\frac{1}{n+1}, \frac{1}{n}[$ donc pour arriver à une telle précision il faut calculer les $10^{20}$ premiers termes de la série !
En supposant qu'Euler était un champion du calcul capable de faire trois opérations arithmétiques correctes par seconde, il aurait fallu à M. Euler pour accomplir cette tache presque
C’est plus que l’âge de la Terre ! (en faite, c'est presque 700 fois l'âge de la Terre )
Si on imagine qu''à chaque opération arithmétique, on fait un pas de 70cm, on pourrait alors faire l'aller-retour vers l'étoile Proxima du Centaure à plusieurs reprises!
Si vous êtes un peu plus rapide, vous pouvez alors faire le tour de notre galaxie.
Vous l'avez compris, Euler était très intelligent pour ne pas commencer une telle aventure!
Mais alors comment a-t-il pu faire ce calcul ?
Bon, M.Euler n'avait pas d'ordinateur, alors que nous on en a! donc pourquoi s'embêter?
Je me suis aussi posé cette question, mais mon génial de PC n'a pas une précision fiable à ce point! Pour lui le zéro est presque égale à $10^{-16}$, mais ce problème peut être corrigé dans Python avec le module Decimal.
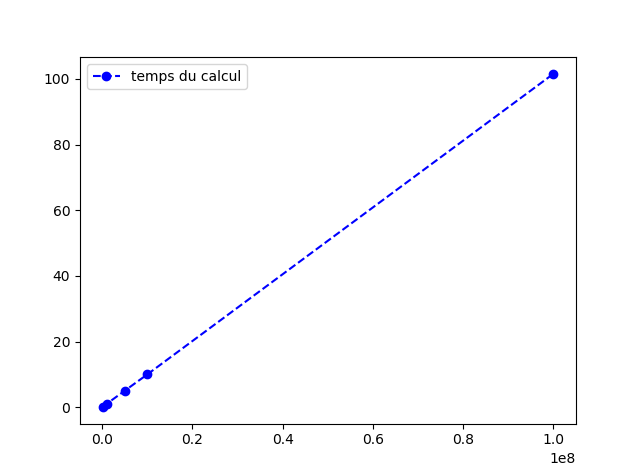
Alors, j'ai un autre problème, le temps de calcul. Sur un PC perssonnel, le temps de calcul pour $n=10^8$ est de l'ordre de $100$ secondes, comme ce temps est linéaire par rapport à $n$, on peut deviner que pour $n=10^{20}$ il faut plus de 3 millions d'années!
Notre objectif dans la suite est de faire ce calcul, de sorte qu’on puisse le terminer dans un temps relativement correct.
Posons dans la suite, pour $n\geq 1$ $$U_n =\dsum_{k=1}^n \dfrac{1}{k^2},\, \, R_n=\dsum_{k\geq n+1} \dfrac{1}{k^2} \text{ (reste d'ordre $n$)}.$$ Et, enfin, $U=U_n+R_n = \dsum_{k\geq 1} \dfrac{1}{k^2}$ la somme de cette série, est donc le réel qu'on souhaite approcher.
Un peu de théorie
La convergence de cette série ne pose aucun problème, en effet, $$\forall n \geq 2,\,\, 0< \dfrac{1}{n^2}\leq \dfrac{1}{n(n-1)}=\frac{1}{n-1}-\frac1n$$ ce qui implique, $$\forall N\geq 2,\, \dsum_{k=1}^N\frac{1}{k^2}\leq 1+\dsum_{k=2}^N\dfrac{1}{k(k-1)}=1+1-\dfrac{1}{N}\leq 2$$ Ainsi la suite $\left(U_n\right)_{n\geq 1}$ est majorée, comme elle est croissante donc elle converge.
Une comparaison série-intégrale donne rapidement que $R_n \in ]\frac{1}{n+1}, \frac{1}{n}[$. En effet, la fonction $x\longmapsto\dfrac{1}{x^2}$ est strictement décroissante sur $\R_+^*$, donc $$\forall n\geq 2,\quad \int_n^{n+1}\dfrac{\ud t}{t^2}\leq \dfrac{1}{n^2}\leq \int_{n-1}^{n}\dfrac{\ud t}{t^2}.$$ Donc, pour $n\geq 1$ et $k\geq n+1$, on obtient $$\int_{n+1}^\infty \dfrac{\ud t}{t^2}= \dsum_{k=n+1}^\infty \int_k^{k+1} \dfrac{\ud t}{t^2} \leq R_n \leq \dsum_{k=n+1}^\infty \int_{k-1}^{k} \dfrac{\ud t}{t^2}=\int_n^\infty\dfrac{\ud t}{t^2}.$$
1ère tentative
Puisque $R_n$ est dans l'intervalle $I_n=]\frac{1}{n+1},\frac{1}{n}[$ alors une idée très simple consiste à remplacer $R_n$ par le milieu de l'intervalle $I_n$, ainsi, on pose $$\forall n\geq 1,\quad V_n=\dsum_{k=1}^n\frac{1}{k^2}+\dfrac{1}{2} \left(\frac{1}{n+1}+\frac{1}{n}\right).$$ De sorte que, $$\abs{U-V_n} =\abs{U_n+R_n -U_n-\dfrac{1}{2} \left(\frac{1}{n+1}+\frac{1}{n}\right)}\leq \dfrac{1}{2}\left(\dfrac{1}{n}-\dfrac{1}{n+1}\right)\leq \dfrac{1}{2n^2}$$ Ainsi pour avoir une erreur inférieure à $10^{20}$, il faut prendre $$n\geq \dfrac{10^{10}}{\sqrt{2}} =7\, 071\, 067 \,811$$ donc avec nos hypothèses sur la vitesse de calcul de M. Euler, il faut pour réaliser ce calcul:
On constate qu'en réalité, on atteint la précision demandée bien avant (exactement pour $n=3\,218\,298$), mais la majoration qu'on a fait ne permet pas d'utiliser cette valeur.
Le temps d'un match PSG-OM
L’idée principale est donc de remplacer le reste $R_n$ par une valeur assez proche de celui-ci, à condition que le coût de calcul de cette valeur approchée soit relativement petit.
Posons alors, pour $n\geq 1$, $$R_n = \dfrac{1}{n} +\dfrac{a}{n^2}+\dfrac{b}{n^3}, \text{ et } W_n =U_n + \dfrac{1}{n} +\dfrac{a}{n^2}+\dfrac{b}{n^3},$$ On pose aussi, pour $n\geq 2$, $\delta_n =W_{n-1}-W_n$, Un calcul simple nous donne $$d_n= \dfrac{(2a+1)n^3+(3b-2-3a)n^2+(a-3b+1)n+b}{(n-1)^3n^3}.$$ Il faut choisir alors $a,\,b$ de sorte que $\delta_n$ soit le plus petit possible.
le choix de $a =-1/2$, $b=1/6$ nous donne alors $$\delta_n=\dfrac{1}{6n^3(n-1)^3}.$$ Bien évidemment, comme la suite $(W_n)$ admet une limite finie lorsque $n$ tend vers $\infty$, alors la série $\dsum \delta_n$ converge, on souhaite alors estimer le reste de cette série qu’on va noter $R_n''$. On a $$\forall n\geq 2,\quad \delta_n ≤ \dfrac{1}{6(n-1)^6}$$ et la fonction $x\longmapsto 1/(x-1)^6$ est décroissante sur $]1,\infty[$ donc en utilisant la comparaison série intégrale on obtient $$\forall n\geq 2,\, R_n''=\dsum_{k\geq n+1}\delta_k \leq \dsum_{k\geq n+1}\dfrac{1}{6(k-1)^6}\leq \int_n^\infty\dfrac{\ud x}{6(x-1)^6}= \dfrac{1}{30(n-1)^5}$$ D’autre part un calcul direct de $R_n''$ nous donne $$ \begin{array}{lcl} 0\leq R_n''&=&\dsum_{k=n+1}^\infty W_{k-1}-W_k\\ &=&W_n-\dsp\lim_{k\to \infty} W_k\\ &=& W_n-U \Longrightarrow U\leq W_n. \end{array} $$ donc on obtient finalement $$w_n -\dfrac{1}{30(n-1)^5}≤ U ≤ w_n$$ Ainsi si on choisit n assez grand de sorte que $\dfrac{1}{30(n-1)^5}$ soit plus petit que $10^{-20}$ on obtient l'approximation demandée de $U$ donc $$10^{20} ≤ 30(n-1)^5 \text{ ce qui donne } 5065 ≤ n$$ soit un temps de calcul
Il s’agit la d’une avancée significative, mais le problème si on commence le calcul en même temps que le début de match PSG-OM, on risque alors de rater la fin de ce match (un match de foot dure au moins 1h45 minutes avec la pause)!
Puisque $U$ est dans l’intervalle $]w_n -\dfrac{1}{30(n-1)^5},w_n[$ alors on posera comme approximation de $U$ la moitié de l’intervalle, ceci alors permet d’obtenir $n = 4410$ soit presque
Le temps d'une pause café !
Le gain obtenu dans la partie précédente est significatif et encourageant! alors ne changeons pas une équipe qui gagne!
On va utiliser la même idée, mais en poussant un peu loin le DL (tout en gardant en tête que le calcul de l'approximation de $R_n$ ne doit pas être compliqué), posons à nouveau: $$\forall n\geq 1,\quad W_n =U_n +\dfrac{1}{n}-\dfrac{1}{2n^2}+\dfrac{1}{6n^3}+\dfrac{a}{n^4}+\dfrac{b}{n^5},$$ et $$\forall n\geq 2, \quad \delta_n = W_{n-1}-W_n.$$ Alors un calcul (un peu moins simple que la dernière fois), nous donne: $$ \forall n\geq 2,\quad \delta_n = \dfrac{1}{6} \dfrac{24an^5+(30b-60a+1)n^4+(60a-60b-2)n^3+(60b-30a+1)n^2+(6a-30b)n+6b}{ (n-1)^5n^5} $$ Le choix de $a=0$ et $b=-1/30$ donne $$\delta_n = \dfrac{-1}{30}\dfrac{5n^2-5n+1}{n^5(n-1)^5}$$ Comme $-5n+1< 0$ pour $n\geq 2$, on obtient $$\forall n\geq 2,\quad 0\leq -\delta_n \leq \dfrac{1}{30} \dfrac{5n^2}{n^5(n-1)^5}\leq \dfrac{1}{6}\dfrac{1}{(n-1)^8}.$$ La fonction $x\longmapsto \dfrac{1}{6(x-1)^8}$ est décroissante sur $]1,\infty[$, donc la comparaison série-intégrale nous donne: $$\forall n\geq 3,\quad 0\leq -R_n''=\dsum_{k\geq n+1}-\delta_k\leq \int_{n}^\infty\dfrac{\ud t}{6(t-1)^8}=\dfrac{1}{42 (n-1)^7}.$$ D'autre part, $$\forall n\geq 2,\, -R_n''= -\dsum_{k\geq n+1}\delta_k=\dsum_{k\geq n+1}W_k-W_{k-1}=U-W_n.$$ On en déduit alors, $$\forall n\geq 2,\quad W_n\leq U\leq W_n+\dfrac{1}{42 (n-1)^7}.$$ Donc pour chercher une approximation de $U$ à $10^{-20}$ il suffit de choisir $n$ tel que $$ \dfrac{1}{42 (n-1)^7}\leq 10^{-20}\Longrightarrow \dfrac{10^{20}}{42}\leq (n-1)^7 \text{\,i.e\, } n\geq 423$$ Donc pour $n=423$, il nous faut (toujours d'après nos hypothèses)